TS Inter 1st Year Maths 1B Solutions Chapter 3 Straight Lines Ex 3(a)

Students must practice these TS Intermediate Maths 1B Solutions Chapter 3 Straight Lines Ex 3(a) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1B Straight Lines Solutions Exercise 3(a)

I.
Question 1.
Find the slopes of the lines x + y = 0 and x – y = 0. (V.S.A.Q.)
Answer:
Slope of x + y = 0 is – \(\frac{a}{b}\) = – 1
Slope of x – y = 0 is 1

Question 2.
Find the equation of the line containing the points (2, -3 ) and (0, – 3 ). (V.S.A.Q.)
Answer:
Equation of the line is \(\frac{y-y_1}{y_1-y_2}=\frac{x-x_1}{x_1-x_2}\)
⇒ \(\frac{y+3}{-3+3}=\frac{x-2}{2-0}\) ⇒ \(\frac{y+3}{0}=\frac{x-2}{2}\)
⇒ 2y + 6 = 0 ⇒ y + 3 = 0

Question 3.
Find the equation of the line containing the points (1, 2) and (1, – 2). (V.S.A.Q.)
Answer:
Equation of the line is \(\frac{y-y_1}{y_1-y_2}=\frac{x-x_1}{x_1-x_2}\)
⇒ \(\frac{y-2}{2+2}=\frac{x-1}{1-1}\)
⇒ (y – 2) (0) = (x – 1) 4
⇒ x – 1 = 0

Question 4.
Find the angle which the straight line y = √3x – 4 makes with the Y-axis. (V.S.A.Q.)
Answer:
Equation of the line is y = √3x – 4
Slope m = √3 = tan\(\frac{\pi}{3}\)
Angle made with X- axis = \(\frac{\pi}{3}\)
∴ Angle made with Y – axis = \(\frac{\pi}{2}-\frac{\pi}{3}\) = \(\frac{\pi}{6}\)

Question 5.
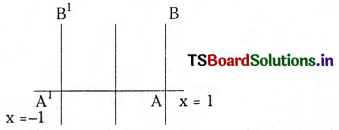
Write the equation of reflection of the line x = 1 in the Y-axis. (V.S.A.Q.)
Answer:
Equation of AB is x = 1. Reflection about Y – axis is x = – 1 i.e., x + 1 = 0

Question 6.
Find the condition for the points ( a, 0 ), (h, k ) and ( 0, b ) where ab * 0, to be collinear. (V.S.A.Q.)
Answer:
Let A (a, 0), B (h, k) and C (0, b) are collinear
Slope of AB = \(\frac{\mathrm{k}-0}{\mathrm{~h}-\mathrm{a}}\)
Slope of AC = \(\frac{0-b}{a-0}\) = \(\frac{-b}{a}\)
Since A,B,C are collinear
slope of AB = slope of AC
⇒ \(\frac{k}{h-a}=\frac{-b}{a}\)
⇒ ak = – bh + ab
⇒ ak + bh = ab
⇒ \(\frac{h}{a}+\frac{k}{b}\) = 1

Question 7.
Write the equations of the straight lines parallel to X-axis and
(i) at a distance of 3 units above the X-axis and
(ii) at a distance of 4 units below the X-axis. (V.S.A.Q.)
Answer:
(i) Equation of straight line parallel to X-axis which is at a distance of 3 units above the X – axis is y = 3 ⇒ y – 3 = 0
(ii) Equation of straight line parallel to X-axis which is at a distance of 4 units below the X- axis is y = -4 ⇒ y + 4 = 0

Question 8.
Write the equations of the straight lines parallel to Y-axis and
(i) at a distance of 2 units from the Y-axis to the right of it
(ii) at a distance of 5 units from the Y-axis to the left of it. (V.S.A.Q.)
Answer:
Equation of straight line parallel to Y – axis and
(i) At a distance of 2 units from the Y – axis to the right of it is x = 2 or x – 2 = 0

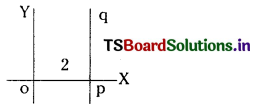
(ii) Equation of the straight line parallel to Y- axis and at a distance of 5 units from the Y-axis to the left of it is x = – 5 or

II.
Question 1.
Find the slopes of the straight lines passing through the following pairs of points
(i) (-3, 8), (10, 5)
(ii) (3, 4), (7, -6)
(iii) (8, 1), (-1, 7)
(iv) ( – P, q ), ( q, – P), ( pq ≠ 0 ) (S.A.Q.)
Answer:
(i) (- 3, 8) ( 10, 5)
Slope = \(\frac{y_1-y_2}{x_1-x_2}=\frac{8-5}{-3-10}=\frac{3}{-13}\)

(ii) (3, 4), (7, – 6)
Slope = \(\frac{4+6}{3-7}=\frac{10}{-4}\)

(ii) (8 ,1), (-1, 7)
Slope = \(\frac{1-7}{8+1}=\frac{-6}{9}=\frac{-2}{3}\)

(iv) ( -P, q ), ( q, – P )
Slope = \(\frac{q+p}{-p-q}=\frac{q+p}{-(p+q)}\) = – 1

Question 2.
Find the value of x, if the slope of the line passing through (2, 5) and (x, 3) is 2. (S.A.Q.)
Answer:
Slope = \(\frac{y_1-y_2}{x_1-x_2}=\frac{5-3}{2-x}\)
Given that slope is ‘2’
∴ \(\frac{2}{2-x}\) = 2 ⇒ 2 – x = 1 ⇒ x = 2 – 1 = 1 ⇒ x = 1

Question 3.
Find the value of y, if the line joining the points ( 3, y ) and ( 2, 7 ) is parallel to the line joining the points (-1, 4) and (0, 6). (Mar. 14) (S.A.Q.)
Answer:
Let A = ( 3, y ), B = ( 2, 7 ), C = ( -1, 4 ) and D = (0, 6) are given points.
m₁ = Slope of AB = \(\frac{\mathrm{y}-7}{3-2}\) = y – 7
m₂ = Slope of CD = \(\frac{4-6}{-1-0}=\frac{-2}{-1}\) = 2
AB and CD are parallel ⇒ Slopes are equal
∴ m₁ = m₂ ⇒ y – 7 = 2
⇒ y = 9

Question 4.
Find the slopes of the lines (i) parallel to and (IQ perpendicular to the line passing through (6, 3) and ( -4, 5 ). (S.A.Q.)
Answer:
Let A = (6, 3), B = (- 4, 5) be the given points.
Slope of AB = \(\) = m
(i) Slope of the line parallel to AB = \(\frac{3-5}{6+4}=\frac{-2}{10}=-\frac{1}{5}\)
(ii) Slope of the line perpendicular to AB = – \(\frac{1}{m}\) = 5

Question 5.
Find the equations of the straight lines which make the following angles with the positive X – axis in the positive direction and which passes through the points given below.
(i) \(\frac{\pi}{4}\) and ( 0, 0 ).
(ii) \(\frac{\pi}{3}\) and (1, 2)
(iii) 135° and (3, -2)
(iv) 150° and (-2, -1)
Answer:
(i) \(\frac{\pi}{4}\) and (0, 0).
m = Slope = tan 45° = 1
Equation of the line is y – y₁ = m(x – x₁)
∴ Equation of the line passing through
(0, 0) with slope ‘1’ is
y – 0 = 1 (x – 0) ⇒ x – y = 0

(ii) \(\frac{\pi}{3}\) and (1, 2 )
m = tan \(\frac{\pi}{3}\) = √3 and equation of line passing through (1, 2) with slope √3 is
y – 2 = √3 (x – 1) ⇒ √3x – y + (2 – √3) = 0

(iii) 135° and (3,-2)
m = tan 135° = tan (180° – 45°) = – tan 45° = – 1
∴ Equation of line passing through (3, – 2) with -1 as slope is
y + 2 = -1 (x – 3)
⇒ y + 2 = – x + 3
⇒ x + y – 1 = 0

(iv) 150° and (-2, -1)
m = tan 150° = tan(180° – 30°)
= – tan 30° = – \(\frac{1}{\sqrt{3}}\)
∴ Equation of line passing through (- 2, – 1) with slope – \(\frac{1}{\sqrt{3}}\) is
y + 1 = – \(\frac{1}{\sqrt{3}}\) (x + 2)
⇒ √3y + √3 = – x – 2
⇒ x + √3y + (2+ √3) = 0

Question 6.
Find the equations of the straight lines passing through the origin and making equal angles with the coordinate axes. (S.A.Q.)
Answer:

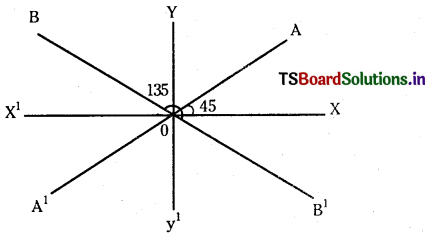
Case (i): AA¹ makes an angle 45° with the positive X – axis m = tan 45° = 1
AA¹ passes through O (0, 0)
Equation of AA¹ is y – 0 = 1 (x – 0) ⇒ x – y = 0

Case (ii): BB¹ makes an angle 135° with positive X – axis
m = tan 135° = tan (180° – 45°) = – tan 45°
Equation of BB¹ is y – 0 = – 1 (x – 0) = – 1 ⇒ x + y = 0

Question 7.
The angle made by a straight line with the positive X – axis in the positive direction and the Y – intercept cut off by it are given below. Find the equation of the straight line. (S.A.Q.)
(i) 60°, 3
(ii) 150°, 2
(iii) 45°, -2
(iv) tan^-1 \(\left(\frac{2}{3}\right)\), 3
Answer:
(i) 60°, 3
We have the equation of a line with Y- intercept ‘c’ and slope m is y = mx + c
m = tan 60° = √3 , c = 3
∴ Equation of the line is y = √3 x + 3
⇒ √3x – y + 3 = 0

(ii) 150°, 2
m = tan 150° = tan (180° – 30°) = – tan 30° = – \(\frac{1}{\sqrt{3}}\), c = 2
∴ Equation of the line is y = – \(\frac{1}{\sqrt{3}}\)x + 2
⇒ √y = – x +2√3
⇒ √3 y + x = 2√3

(iii) 45°, -2
m = tan 45° = 1, c = – 2
∴ Equation of the line is y = x – 2
⇒ x – y – 2 = 0

(iv) tan^-1\(\left(\frac{2}{3}\right)\), 3
⇒ θ = tan^-1 ⇒ m = tan θ = \(\frac{2}{3}\), c = 3
∴ Equation of the line is y = \(\frac{2}{3}\)x + 3
⇒ 3y = 2x + 9
⇒ 2x – 3y + 9 = 0

Question 8.
Find the equation of the straight line passing through (- 4, 5) and cutting off equal and non-zero intercepts on the coordinate axes. (S.A.Q.)
Answer:
Equation of the straight line in the intercept form is \(\frac{x}{a}+\frac{y}{b}\) = 1
Given equal and non – zero intercept s ⇒ a = b
Equation of the line is \(\frac{x}{a}+\frac{y}{b}\) = 1 ⇒ x + y = a
This line passes through P (- 4, 5) ⇒ 4 + 5 = a ⇒ a = 1
∴ Equation of the required line is x + y – 1 = 0

Question 9.
Find the equation of the straight line passing through (- 2, 4 ) and making non-zero intercepts whose sum is zero. (S.A.Q.)
Answer:
Equation of the line in the intercept form is \(\frac{x}{a}+\frac{y}{b}\) = 1
a b
Given a + b = 0 ⇒ b = -a
∴ Equation of the line is x – y = a
This line passes through P (- 2, 4)
∴ – 2 – 4 = a ⇒ a = – 6
∴ Equation of the required line is x – y + 6 = 0

III.
Question 1.
Find the equation of the straight line passing through the point ( 3, -4 ) and making X and Y – intercepts which are in the ratio 2 : 3. (E.Q.)
Answer:
Equation of the line in the intercept form is
\(\frac{\mathrm{x}}{\mathrm{a}}+\frac{\mathrm{y}}{\mathrm{b}}\) = 1
Given a : b = 2 : 3
⇒ \(\frac{\mathrm{a}}{\mathrm{b}}=\frac{2}{3}\) ⇒ b = \(\frac{3 a}{2}\)
Equation of the line is \(\frac{x}{a}+\frac{2 y}{3 a}\) = 1
⇒ 3x + 2y = 3a
The line passes through the point p(3, – 4) then 9 – 8 = 3a ⇒ 3a = 1 ⇒ a = \(\frac{1}{3}\)
∴ Equation of the required line is 3x + 2y = 1
⇒ 3x + 2y – 1 = 0

Question 2.
Find the equation of the straight line passing through the point (4, -3) and perpendicular to the line passing through the points (1, 1) and (2, 3 ). (E.Q.)
Answer:
Let A = (1, 1) and B = (2, 3) be the given points.
m = Slope of AB = \(\frac{1-3}{1-2}\) = 2 = m ( suppose)
∴ Slope of the perpendicular line is \(-\left(\frac{1}{m}\right)=-\frac{1}{2}\)
∴ Equation of the line passing through (4, -3) with slope – \(\frac{1}{2}\) is y – y₁ = m (x – x₁)
⇒ y + 3 = – \(\frac{1}{2}\) (x – 4)
⇒ 2y + 6 = – x + 4
⇒ x + 2y + 2 = 0

Question 3.
Show that the following sets of points are collinear and find the equation of the line L containing them,
(i) (- 5, 1), (5, 5), (10, 7)
(ii) (1, 3), (-2, -6), (2, 6)
(iii) (a, b + c), (b, c + a), (c, a + b) (E.Q.)
Answer:
(i) Let A (-5, 1), B (5, 5), C (10, 7) be the given points.
Equation of AB is \(\frac{y-y_1}{y_1-y_2}=\frac{x-x_1}{x_1-x_2}\)
⇒ \(\frac{y-1}{1-5}=\frac{x+5}{-5-5}\)
⇒ \(\frac{y-1}{-4}=\frac{x+5}{-10}\)
⇒ – 4x – 20 = – 10y + 10
⇒ 4x – 10y + 30 = 0
⇒ 2x – 5y + 15 = 0
If C (10, 7) lies on the above line then 2(10) – 5 (7) + 15 = 20 – 35 + 15 = 0
Hence A, B, C are collinear and equation of line containing the points is 2x – 5y + 15 = 0

(ii) Let A (1, 3), B (-2, -6), C (2, 6) be the given points. Then equation of AB is
(y – 3 ) (1 + 2) = (x – 1) (3 + 6)
⇒ 3(y – 3) = 9(x – 1)
⇒ y – 3 = 3(x – 1)
⇒ 3x – y = 0
If C (2, 6) lies on the above line then 3(2) – 6 = 6 – 6 = 0
Hence A, B, C are collinear and equation of line containing these points is 3x – y = 0

(iii) Let A ( a, b + c), B ( b, c + a) ; C ( c, a + b) be the given points.
Equation of AB is
[y – (b + c)l (a – b) = (x – a) ( b + c – c – a)
⇒ (y – b – c) (a – b) = – (a – b) ( x – a)
⇒ y – b – c = – x + a ⇒ x + y – (a + b + c) = 0
If the point (c, a + b) lies on the lines then c + a + b – a – b – c = 0
∴ A, B, C are collinear and the equation of the line containing the points is
x + y = a + b + c

Question 4.
A (10, 4), B (- 4, 9) and C (- 2, -1) are the vertices of a triangle. Find the equations of
(i) \(\overleftrightarrow{\mathbf{A B}}\)
(ii) the median through A
(iii) the altitude through B
(iv) the perpendicular bisector of the side \(\overleftrightarrow{\mathbf{A B}}\). (E.Q.)
Answer:
Given A ( 10, 4 ), B ( – 4, 9 ) and C =( – 2, – 1)

(i) The equation of AB is
(y – 4) ( 10 + 4) = ( x – 10) ( 4 – 9)
⇒ 14y – 56 = – 5x + 50
⇒ 5x + 14y – 106 = 0

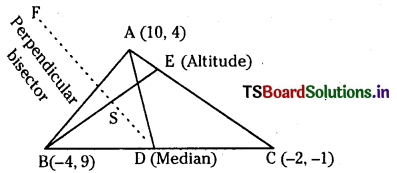
(ii) D is the midpoint of BC and AD is the Median through A coordinates of D are
\(\left(\frac{-4-2}{2}, \frac{9-1}{2}\right)\) = (- 3, 4)
∴ Equator of Median AD is
(y – 4) ( 10 + 3) = ( x + 3) ( 4 – 4)
⇒ 13 (y – 4) = 0
⇒ y – 4 = 0 ⇒ y = 4

(iii) BE is the altitude through B, perpendicular to AC
Slope of AC = \(\frac{4+1}{10+2}=\frac{5}{12}\)
∴ Slope of BE = – \(\frac{12}{5}\)
∴ Equation of altitude BC is
y – 9 = – \(\frac{12}{5}\) ( x + 4)
⇒ 5y – 45 = – 12x – 48
⇒ 12x + 5y + 3 = 0

(iv) Mid point of AB = \(\left(\frac{10-4}{2}, \frac{4+9}{2}\right)\)
∴ F = \(\left(3, \frac{13}{2}\right)\)
Slope of AB = \(\frac{4-9}{10+4}=-\frac{5}{14}\)
∴ Slope of perpendicular bisector SF is = \(\overline{\mathrm{AB}}\)
∴ Equation of the perpendicular bisector of the side AB is
y – \(\frac{13}{2}\) = \(\frac{14}{5}\) (x – 3)
⇒ \(\frac{2 y-13}{2}\) = \(\frac{14}{5}\) (x – 3)
⇒ 10y – 65 = 28 ( x – 3)
⇒ 28x – 10y – 19 = 0