TS Inter 1st Year Maths 1B The Plane Important Questions

Students must practice these Maths 1B Important Questions TS Inter 1st Year Maths 1B The Plane Important Questions to help strengthen their preparations for exams.

TS Inter 1st Year Maths 1B The Plane Important Questions

Question 1.
Reduce the equation x + 2y – 3z – 6 = 0 of the plane to the normal form. [Mar. ’19 (TS); Mar. ’16 (AP & TS), ’14, ’01; May ’13]
Solution:
Given the equation of the plane is,
x + 2y – 3z – 6 = 0
x + 2y – 3z = 6
On dividing both sides by

∴ which is the normal form.

Question 2.
Find the equation of the plane whose intercepts on X, Y, Z axes are 1, 2, 4 respectively. [May ’14; Mar ’10]
Solution:
Given that,
x-intercept, a = 1
y-intercept, b = 2
z-intercept, c = 4
∴ The equation of the plane is

4x + 2y + z = 4

Question 3.
Find the directions of the normal to the plane x + 2y + 2z – 4 = 0. [May ’15 (TS); Mar. ’13; May ’12]
Solution:
Given, equation of the plane is x + 2y + 2z – 4 = 0
Directions ratio’s of the normal to the plane are (a, b, c) = (1, 2, 2).
Directions cosines of the normal

Question 4.
Write the equation of the plane 4x – 4y + 2z + 5 = 0 in the intercept form. [Mar. ’19 (AP); Mar. ’12]
Solution:
Given, equation of the plane is 4x – 4y + 2z + 5 = 0
4x – 4y + 2z = -5
\(\frac{4 x}{-5}-\frac{4 y}{-5}+\frac{2 z}{-5}=1\)
\(\frac{x}{\frac{-5}{4}}-\frac{y}{\frac{-5}{4}}+\frac{z}{\frac{-5}{2}}=1\)
which is the intercept form.

Question 5.
Find the angle between the planes x + 2y + 2z – 5 = 0 and 3x + 3y + 2z – 8 = 0. [Mar. ’17, ’15 (TS), ’09 ; May ’15 (AP)]
Solution:
Given equations of the planes are
x + 2y + 2z – 5 = 0 ……….(1)
3x + 3y + 2z – 8 = 0 ……..(2)
Comparing (1) with a₁x + b₁y + c₁z + d₁ = 0, we get
a₁ = 1, b₁ = 2, c₁ = 2, d₁ = -5
Comparing (2) with a₂x + b₂y + c₂z + d₂ = 0, we get
a₂ = 3, b₂ = 3, c₂ = 2, d₂ = -8
If ‘θ’ is the angle between the planes (1) & (2) then

Question 6.
Find the equation of the plane passing through (1, 1, 1) and parallel to the plane x + 2y + 3z – 7 = 0. [May ’13 (Old), ’11, ’10, ’09]
Solution:
Given, the equation of the plane is
x + 2y + 3z – 7 = 0 ……….(1)
Let the given point P = (1, 1, 1)
The equation of any plane parallel to x + 2y + 3z – 7 = 0 is x + 2y + 3z + k = 0
If equation (1) passes through the point p(1, 1, 1), then
1 + 2(1) + 3(1) + k = 0
1 + 2 + 3 + k = 0
6 + k = 0
k = -6
Substituting the value of ‘k’ in equation (1)
∴ The equation of the required plane is x + 2y + 3z – 6 = 0

Question 7.
Find the equation of the plane bisecting the line segment joining (2, 0, 6) and (-6, 2, 4) and perpendicular to it.
Solution:
Let A(2, 0, 6), B(-6, 2, 4) are the given points

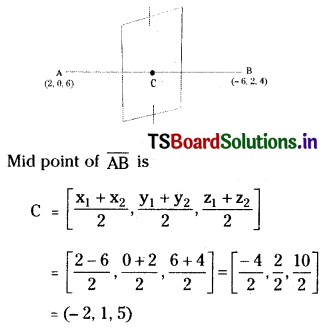
Directions of \(\overline{\mathrm{AB}}\) are (x₂ – x₁, y₂ – y₁, z₂ – z₁)
= (-6 – 2, 2 – 0, 4 – 6)
= (-8, 2, -2)
= (a, b, c)
Since the plane is ⊥ to \(\overline{\mathrm{AB}}\) then the line \(\overline{\mathrm{AB}}\) is normal to the plane.
Also, ‘C'(-2, 1, 5) lies in the plane.
∴ The equation of the plane passing through C(-2, 1, 5) & having direction ratios of the normal to the plane is (-8, 2, -2) is a(x – x₁) + b(y – y₁) + c(z – z₁) = 0
⇒ -8(x + 2) + 2(y – 1) – 2(z – 5) = 0
⇒ -8x – 16 + 2y – 2 – 2z + 10 = 0
⇒ -8x + 2y – 2x – 8 = 0
⇒ 4x – y + z + 4 = 0

Question 8.
Find the equation of the plane through the points (2, 2, -1), (3, 4, 2), (7, 0, 6). [May ’00]
Solution:
Let the given points are
A(x₁, y₁, z₁) = (2, 2, -1)
B(x₂, y₂, z₂) = (3, 4, 2)
C(x₃, y₃, z₃) = (7, 0, 6)
The equation of the plane passing through the points A(2, 2, -1), B(3, 4, 2), C(7, 0, 6) is

(x – 2)(14 + 6) – (y – 2)(7 – 15) + (z + 1)(-2 – 10) = 0
(x – 2)(20) – (y – 2)(-8) + (z + 1)(-12) = 0
(x – 2)(5) – (y – 2)(-2) + (z + 1)(-3) = 0
5x – 10 + 2y – 4 – 3z – 3 = 0
5x + 2y – 3z – 17 = 0

Question 9.
A plane meets the coordinate axes in A, B, C. If the centroid of ∆ABC is (a, b, c) show that the equation to the plane is \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=3\). [Mar. ’01]
Solution:
Let the equation of the plane be
\(\frac{x}{p}+\frac{y}{q}+\frac{z}{r}=1\) ……..(1)

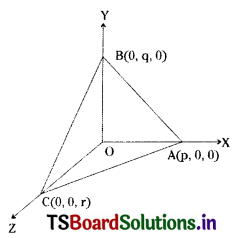
Plane (1) cuts the X-axis, Y-axis & Z-axis at A, B, C respectively.
Then, A = (p, 0, 0), B = (0, q, 0), C = (0, 0, r)
The centroid of triangle ABC is

Given that, the centroid of triangle ABC is G = (a, b, c)
∴ (a, b, c) = \(\left(\frac{\mathrm{p}}{3}, \frac{\mathrm{q}}{3}, \frac{\mathrm{r}}{3}\right)\)
a = \(\frac{p}{3}\), b = \(\frac{q}{3}\), c = \(\frac{r}{3}\)
p = 3a, q = 3b, r = 3c
∴ The equation to the required plane is from (1)

Some More Maths 1B The Plane Important Questions

Question 10.
Find the angle between the planes, 2x – y + z = 6 and x + y + 2z = 7. [Mar. ’11; B.P.]
Solution:
Given equations of the plane are
2x – y + z = 6 ……..(1)
x + y + 2z = 7 ……..(2)
Comparing (1) with a₁x + b₁y + c₁z + d₁ = 0, we get
a₁ = 2, b₁ = -1, c₁ = 1, d₁ = -6
Comparing (2) with a₂x + b₂y + c₂z + d₂ = 0, we get
a₂ = 1, b₂ = 1, c₂ = 2, d₂ = -7
If ‘θ’ is the angle between the planes (1) & (2) then

Question 11.
Find the equation of the plane through the point (α, β, γ) and parallel to the plane ax + by + cz = 0.
Solution:
Given the equation of the plane is
ax + by + cz = 0 ………(1)
Let the given point p = (α, β, γ)
∴ The equation of any plane parallel to ax + by + cz = 0 is ax + by + cz + k = 0
If equation (1) passes through the point p(α, β, γ) then
a(α) + b(β) + c(γ) + k = 0
⇒ k = -aα – bβ – cγ
Substituting the value of ‘k’ in equation (1)
∴ The equation of the required plane is ax + by + cz – aα – bβ – cγ = 0
a(x – α) + b(y – β) + c(z – γ) = 0

Question 12.
Show that the plane through (1, 1, 1), (1, -1, 1), and (-7, -3, -5) is parallel to Y-axis.
Solution:
Let the given points are
A(x₁, y₁, z₁) = (1, 1, 1)
B(x₂, y₂, z₂) = (1, -1, 1)
C(x₃, y₃, z₃) = (-7, -3, -5)
The equation of the plane passing through the points A(1, 1, 1), B(1, -1, 1), C(-7, -3, -5) is

(x – 1)(12 – 0) – (y – 1)(0 – 0) + (z – 1)(0 – 16) = 0
(x – 1)(12) – 0 + (z – 1)(-16) = 0
12x – 12 – 16z + 16 = 0
12x – 16z + 4 = 0
3x – 4z + 1 = 0
Since the coefficient of y is zero, the plane is perpendicular to xz-plane and hence the plane is parallel to the y-axis.

Question 13.
Find the equation to the plane through the points (0, -1, -1), (4, 5, 1) and (3, 9, 4).
Solution:
Let the given points are
A(x₁, y₁, z₁) = (0, -1, -1)
B(x₂, y₂, z₂) = (4, 5, 1)
C(x₃, y₃, z₃) = (3, 9, 4)
The equation of the plane passing through the points A(0, -1, -1), B(4, 5, 1), C(3, 9, 4) is


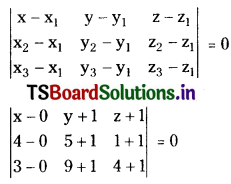
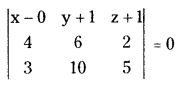
x(30 – 20) – (y + 1)(20 – 6) + (z + 1)(40 – 18) = 0
x(10) – (y + 1)(14) + (z + 1)(22) = 0
10x – 14y – 14 + 22z + 22 = 0
10x – 14y + 22z + 8 = 0
5x – 7y + 11z + 4 = 0

Question 14.
Find the equation of the plane if the foot of the perpendicular from the origin to the plane is (1, 3, -5).
Solution:
Let O(0, 0, 0) be the origin.
P(1, 3, -5) is the foot of the perpendicular.
The plane passing through P and is perpendicular to the line segment \(\overline{\mathrm{OP}}\) is normal to the plane.
Directions of \(\overline{\mathrm{OP}}\) = (x₂ – x₁, y₂ – y₁, z₂ – z₁)
= (1 – 0, 3 – 0, -5 – 0)
= (1, 3, -5)
∴ The equation of the plane passing through P(1, 3, -5) having direction ratios of the normal to the plane are (1, 3, -5) is a(x – x₁) + b(y – y₁) + c(z – z₁) = 0
⇒ 1(x – 1) + 3(y – 3) – 5(z + 5) = 0
⇒ x – 1 + 3y – 9 – 5z – 25 = 0
⇒ x + 3y – 5z – 35 = 0
⇒ x + 3y – 5z = 35

Question 15.
Find the equation of the plane if the foot of the perpendicular from the origin to the plane is (2, 3, -5).
Solution:

Let O(0, 0, 0) be the origin.
P(2, 3, -5) is the foot of the perpendicular.
The plane passing through P is perpendicular to \(\overline{\mathrm{OP}}\) the line segment \(\overline{\mathrm{OP}}\) is normal to the plane.
Directions of \(\overline{\mathrm{OP}}\) are (x₂ – x₁, y₂ – y₁, z₂ – z₁)
= (2 – 0, 3 – 0, -5 – 0)
= (2, 3, -5)
The equation of the plane passing through P(2, 3, -5) having direction ratios of the normal to the plane are (2, 3, -5) is a(x – x₁) + b(y – y₁) + c(z – z₁) = 0
2(x – 2) + 3(y – 3) + (-5)(z + 5) = 0
2x – 4 + 3y – 9 – 10 – 5z = 0
2x + 3y – 5z = 0

Question 16.
Find the intercepts of the plane 4x + 3y – 2z + 2 = 0 on the coordinate axes. [Mar. ’18 (AP & TS)]
Solution:
Given, the equation of the plane is
4x + 3y – 2z + 2 = 0
4x + 3y – 2z = -2

x-intercept, a = \(\frac{-1}{2}\)
y-intercept, b = \(\frac{-2}{3}\)
z-intercept, c = 1

Question 17.
Find the equation of the plane passing through (-2, 1, 3) and having (3, -5, 4) as directions of its normal.
Solution:
Let the given point (x₁, y₁, z₁) = (-2, 1, 3)
Direction ratio’s of the normal to the plane are (a, b, c) = (3, -5, 4)
∴ The equation of the plane passing through the point (-2, 1, 3) and having directions of (3, -5, 4) is a(x – x₁) + b(y – y₁) + c(z – z₁) = 0
3(x + 2) + (-5)(y – 1) + 4(z – 3) = 0
3x + 6 – 5y + 5 + 4z – 12 = 0
3x – 5y + 4z – 1 = 0

Question 18.
Find the equation of the plane passing through (2, 3, 4) and perpendicular to the X-axis.
Solution:
If the plane is perpendicular to X-axis then the plane is parallel to yz-plane.
∴ The equation of a plane parallel to yz axis plane is x = k ……….(1)
If plane (1) passes through the point (2, 3, 4) then
2 = k
∴ k = 2
Substituting the value of k in equation (1)
∴ The equation of the required plane is x = 2.

Question 19.
Find the equation to the plane parallel to the zx-plane and passing through (0, 4, 4).
Solution:
The equation of the plane parallel to zx plane is y = k ……..(1)
If plane (1) passes through point (0, 4, 4) then
4 = k
∴ k = 4
Substituting ‘k’ in equation (1), y = 4
The equation of the required plane is y = 4.

Question 20.
Find the equation of the plane through (-1, 6, 2) and perpendicular to the join of (1, 2, 3) and (-2, 3, 4).
Solution:
Let A(1, 2, 3), B(-2, 3, 4) are the given points
Directions of \(\overline{\mathrm{AB}}\) are (x₂ – x₁, y₂ – y₁, z₂ – z₁)
= (-2 – 1, 3 – 2, 4 – 3)
= (-3, 1, 1)
Directions of normal to the plane are (a, b, c) = (-3, 1, 1)
The equation of the plane passing through (-1, 6, 2) and having directions of normal to the plane are (-3, 1, 1) is a(x – x₁) + b(y – y₁) + c(z – z₁) = 0
-3(x + 1) + 1(y – 6) + 1(z – 2) = 0
-3x – 3 + y – 6 + z – 2 = 0
-3x + y + z – 11 = 0
3x – y – z + 11 = 0