TS Inter 1st Year Maths 1B Solutions Chapter 10 Applications of Derivatives Ex 10(e)

Students must practice this TS Inter 1st Year Maths 1B Study Material Chapter 10 Applications of Derivatives Ex 10(e) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1B Applications of Derivatives Solutions Exercise 10(e)

I.
Question 1.
At time ‘t’ the distance ‘x’ of a particle moving in a straight line is given by s = – 4t² + 2t. Find the average velocity between t = 2 and t = 8 sec. (V.S.A.Q.)
Answer:
s = – 4t² + 2t
∴ v = \(\frac{\mathrm{d} s}{\mathrm{dt}}\) = -8t + 2
Velocity at t = 2 is -16 + 2 = -14 units/sec.
Velocity at t = 8 is – 64 + 2 = – 62 units/sec.
Average velocity between t = 2 and t = 8 sec
= \(\frac{-62-14}{2}\) = – 38 units/sec.

Question 2.
If y = x⁴ then find the average rate of change of y between x = 2 and x = 4. (V.S.A.Q.)
Answer:

Question 3.
A particle moving along a straight line has the relation s = t³ + 2t + 3 connecting the distance s described by a particle in time t. Find the velocity and acceleration of the particle at t = 4 sec. (V.S.A.Q.)
Answer:
s = t³ + 2t + 3

Question 4.
The distance – time formula for the motion of a particle along a straight line is s = t³ – 9t² + 24t – 18. Find when and Where the velocity is zero. (S.A.Q.)
Answer:
Given s = t³ – 9t² + 24t – 18
v = \(\frac{\mathrm{ds}}{\mathrm{dt}}\) = 3t² – 18t + 24
v = 0 ⇒ \(\frac{\mathrm{ds}}{\mathrm{dt}}\) = 0 ⇒ 3 (t² – 6t + 8) = 0
⇒ t = 2 or 4
The velocity is zero after 2 and 4 seconds

Case – (i) :
When t = 2, we have s = t3 – 9t2 + 24t – 18
= 8 – 36 + 48 – 13
= 56 – 54
= 2

Case – (ii) :
When t = 4, we have
s = t3 – 9t2 + 24t – 18
= 64 – 144 + 96- 18
= 160 – 162
= – 2
The particle is at a distance of 2 units from the starting point 0 on either side.

Question 5.
The displacement s of a particle travelling in a straight line in t seconds is given by s = 45t + lit2 – t3. Find the time when the particle comes to rest. (S.A.Q.)
Answer:
s = 45t + 11t² – t³
v = \(\frac{\mathrm{ds}}{\mathrm{dt}}\) = 45 + 22t – 3t²
If the particle comes to rest then v = 0
⇒ 45 + 22t – 3t² = 0
⇒ 3t² – 22t – 45 = 0
⇒ 3t² – 27t + 5t – 45 = 0
⇒ (3t + 5) (t – 9) = 0
⇒ t = \(\frac{-5}{3}\) or t = 9
∴ t = 9 and the particle comes to rest after t = 9 seconds.

II.
Question 1.
The volume of a cube is increasing at the rate of 8 cm3/sec. How fast is the surface area increasing when the length of an edge is 12 cm ? (Mar. ’14) (S.A.Q.)
Answer:
Suppose ‘a’ is the edge of the cube and V be the volume of the cube.
V = a³ ………….(1)

Question 2.
A stone is dropped into a quiet lake and ripples move in circles at the speed of 5 cm/sec. At the instant when the radius of circular ripple is 8 cm, how fast is the enclosed area increases ? (S.A.Q.)
Answer:
Suppose r is the radius of the outer ripple and A be its area.
Then the area A = πr2
dA „ dr dr _
\(\frac{\mathrm{dA}}{\mathrm{dt}}\) = 2πr \(\frac{\mathrm{dr}}{\mathrm{dt}}\); Given r = 8, \(\frac{\mathrm{dr}}{\mathrm{dt}}\) = 5
\(\frac{\mathrm{dA}}{\mathrm{dt}}\) = 2π(8) (5) = 80 π cm² / sec

Question 3.
The radius of a circle is increasing at the rate of 0.7 cm/sec. What is the rate of Increase of its circumference ? (S.A.Q.)
Answer:
Given \(\frac{\mathrm{dr}}{\mathrm{dt}}\) = 0.7 cm/sec at
Circumference C = 2πr
\(\frac{\mathrm{dC}}{\mathrm{dt}}\) = 2π\(\frac{\mathrm{dr}}{\mathrm{dt}}\) = 2π(0.7) = 1.4π cm/sec

Question 4.
A balloon which always remains spherical on inflation is being inflated by pumping in 900 cubic centimeters of gas per second. Find the rate at which the radius of balloon increases when the radius is 15 cm. (S.A.Q.)
Answer:
Given \(\frac{\mathrm{dV}}{\mathrm{dt}}\) = 900 c.c/sec and r = 15 cm
Volume of the sphere V = \(\frac{4}{3}\)πr³

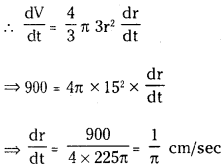
Question 5.
The radius of an air bubble is increasing at the rate of \(\frac{1}{2}\) cm/sec. At what rate is the volume of the bubble is increasing when the radius is 1 cm ? (S.A.Q.)
Answer:
\(\frac{\mathrm{dr}}{\mathrm{dt}}=\frac{1}{2}\) cm/sec end radius r = 1 cm
Given volume of sphere V = \(\frac{4}{3}\)πr³
\(\frac{\mathrm{dV}}{\mathrm{dt}}=\frac{4}{3}\)π3r² = \(\frac{\mathrm{dr}}{\mathrm{dt}}\) = 4πr²\(\frac{\mathrm{dr}}{\mathrm{dt}}\)
= 4π × 1 × \(\frac{1}{2}\) = 2π cm³/sec

Question 6.
Assume that an object is launched upward at 980 m/sec. Its position would be given by s = – 4.9t2 + 9801. Find the maximum height attained by the object. (S.A.Q.)
Answer:
Given relation between s and t as s = – 4.9t² + 980 t
= – 9.8t + 980
For maximum height \(\frac{\mathrm{ds}}{\mathrm{dt}}\) = 0
s = – 4.9 (100)² + 980 (100)
= – 49000 + 98000 = 49000 units
The maximum height attained by the object is 49000 units.

Question 7.
Let a kind of bacteria grow in such a way that at time t sec, there are t3^2 bacteria. Find the rate of growth at time t = 4 hours. (S.A.Q.)
Answer:
Let ‘s’ be the amount of growth of bacteria at time’t’. Then s(t) = t^3/2
The growth rate at time’t’ is given by
\(\frac{\mathrm{ds}}{\mathrm{dt}}=\frac{3}{2}\)
When t = 4, \(\frac{3}{2}\) (4 × 60 × 60)
= \(\frac{3}{2}\) (2 × 60) = 180 units.

Question 8.
Suppose we have a rectangular aquarium with dimensions of length 8 m, width 4 in and height 3 m. Suppose we are filling the tank with water at the rate of 0.4 m3/sec. How feist is the height of water changing when the water level is 3 m ? (S.A.Q.)
Answer:
Length of aquarium l = 8 m
Width of aquarium b = 4 m
Height of aquarium h = 3 m
\(\frac{\mathrm{dV}}{\mathrm{dt}}\) = 0.4 m/sec dt
V = lbh = 8 (4) (3) = 96
and log V = log l + log b + log h
\(\frac{1}{V} \frac{d V}{d t}=\frac{1}{h} \frac{d h}{d t}\) (∵l, b are constants)
⇒ \(\frac{0.4}{96}=\frac{1}{3} \frac{\mathrm{dh}}{\mathrm{dt}}\)
⇒ \(\frac{\mathrm{dh}}{\mathrm{dt}}=\frac{3 \times 0.4}{96}=\frac{1}{80}\)

Question 9.
A container is in the shape of an inverted cone has height 8 m and radius 6 m at the top. If it is filled with water at the rate of 2 m³/minuite how fast is the height of the water changing when the level is 4 m ? (S.A.Q.)
Answer:
Given h = 8 m = OA
r = 6 m = AB

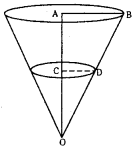
The above measurements are at instant of time’t’
In ΔOAB, ΔOCD we have

Question 10.
The total cost c(x) in rupees associated with the production of x units of an item is given by c(x) = 0. 007 x³ – 0.003 x² + 15x + 4000. Find the marginal cost when 17 units are produced. (S.A.Q.)
Answer:
Let m represents the marginal cost then m = \(\frac{\mathrm{dc}}{\mathrm{dx}}\)
Hence
m = \(\frac{d}{d x}\)(0.007x³ – 0.003x² + 15x + 4000)
= 0.007 (3x²) – 0.003 (2x) + 15
The marginal cost at x = 17 is
(m)_x=17 = 17 = (0.007) (3 × 172) – 0.003 (34) + 15
= (0.007) (3 × 289) – (0.003) (34) + 15
= (0.007) 867 – (0.003) (34) + 15
= 20.967

Question 11.
The total revenue in rupees received from the sale of x units of a produce is given by R(x) = 13x² + 26x + 15. Find the marginal revenue when x = 7. (S.A.Q.)
Answer:
Let m denotes the margin revenue. Then
m = \(\frac{\mathrm{d}}{\mathrm{dx}}\)
Given R(x) = 13x² + 26x + 15 m = 26x + 26
The marginal revenue when x = 7 is
(m)_x=7 = 7= 26 (7) + 26 = 208

Question 12.
A point P is moving on the curve y = 2x². The x coordinate of P is increasing at the rate of 4 units per second. Find the rate at which y coordinate is increasing when the point is at (2, 8). (S.A.Q.)
Given equation of the curve is y = 2x² ………….. (1)
Let P (x₁, y₁) be any point on the curve (1)
Let y₁ = 2x₁
x₁ = 2 and y₁ = 8
Differentiating (2) w.r.t ‘t’
\(\frac{d y_1}{d t}\) = 4x₁ \(\frac{d x_1}{d t}\)
= 4 (2) (4)
= 32 units/sec.
∴ y co-ordinate is increasing at the rate of 32 units/sec.