TS Inter 1st Year Maths 1B Solutions Chapter 10 Applications of Derivatives Ex 10(c)

Students must practice this TS Inter 1st Year Maths 1B Study Material Chapter 10 Applications of Derivatives Ex 10(c) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1B Applications of Derivatives Solutions Exercise 10(c)

I.
Question 1.
Find the length of subtangent and sub¬normal at a point of the curve y = b sin\(\frac{x}{a}\).
Answer:
Equation of the curve is y = b sin\(\left(\frac{x}{a}\right)\)
\(\frac{d y}{d x}\) = b cos\(\left(\frac{x}{a}\right) \cdot \frac{1}{a}=\frac{b}{a}\) cos\(\left(\frac{x}{a}\right)\)

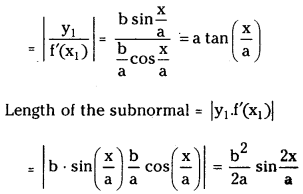
Question 2.
Show that the length of the subnormal at any point in the curve xy = a² varies as the cube of the ordinate of the point. (V.S.A.Q.)
Answer:
Equation of the curve is xy = a²

∴ Length of the subnormal αy₁³ = cube of the ordinate.

Question 3.
Show that at any point (x, y) on the curve y = be^x/a, the length of the subtangent is a constant and the length of the subnormal is \(\frac{y^2}{a}\). (V.S.A.Q)
Answer:
Equation of the given curve is y = be^x/a
∴ \(\frac{d y}{d x}=\frac{b}{a}\)e^x/a = \(\frac{\mathrm{y}}{\mathrm{a}}\)
∴ Slope at any point P(x, y) = \(\frac{y}{a}\)
Length of the subtangent = |y₁/f'(x₁)|
= |y/\(\frac{y}{a}\)| = a = constant
Length of the subnormal = |y₁/f'(x₁)|
= |y.\(\frac{y}{a}\)| = \(\left|\frac{y^2}{a}\right|\)

II.
Question 1.
Find the value of k so that the length of the subnormal at any point on the curve xy^k = a^k+1 is a constant. (S.A.Q.)
Answer:
Equation of the curve is xy^k = a^k+1
Let P(xj, yO be any point on the curve then
x₁y₁^k = a^k+1 …………….(1)
Differentiating w.r. to x,

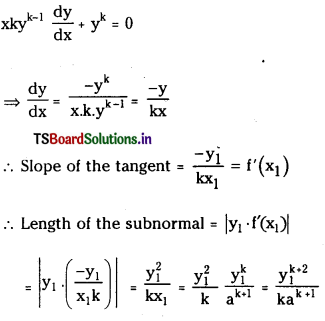
Length of the subnormal is constant at any point on the curve is independent of x₁ and y₁.
\(\frac{\mathrm{y}_1^{\mathrm{k}+2}}{\mathrm{k} \cdot \mathrm{a}^{\mathrm{k}+1}}\) is independent of x₁ y₁.
∴ k + 2 = 0
⇒ k = – 2

Question 2.
At any point t on the curve x = a (t + sin t), y = a (1 – cos t), find the lengths of tangent, normal, subtangent and subnormal. (S.A.Q.) (June 2004, Board Model Paper)
Answer:
Equation of the curve is
x = a (t + sin t), y = a (1 – cos t)

Question 3.
Find the length of normal and subnormal at a point on the curve y = \(\frac{a}{2}\left(e^{\frac{x}{a}}+e^{\frac{-x}{a}}\right)\) (S.AQ.) (March 2013)
Answer:
Equation of the curve is y = \(\frac{a}{2}\left(e^{\frac{x}{a}}+e^{\frac{-x}{a}}\right)\)
= a cos h\(\left(\frac{x}{a}\right)\)

Question 4.
Find the lengths of subtangent, subnormal at a point’t’ on the curve x = a (cos t + t sin t), y = a (sin t – t cos t) (May 2014) (S.A.Q.)
Answer:
Equation of the curve is
x = a (cos t + t sin t)
y = a (sin t – t cos t)
\(\frac{\mathrm{dx}}{\mathrm{dt}}\) = a(-sint + tcost + sint) = at cos t
and \(\frac{\mathrm{dy}}{\mathrm{dt}}\)= a (cost + tsint – cost) = at sin t dt
∴ \(\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{dy}}{\mathrm{dt}} / \frac{\mathrm{dx}}{\mathrm{dt}}=\frac{\mathrm{at} \sin \mathrm{t}}{\mathrm{at} \cos \mathrm{t}}\) = tan t
= \(\left|\frac{\mathrm{a}(\sin \mathrm{t}-\mathrm{t} \cos \mathrm{t})}{\tan \mathrm{t}}\right|\)
= |a cot t(sin t – t cos t)|
Length of the subnormal = |y₁. f'(x₁)|
= |a(sin t – t cos t) tan t|
= |a tan t(sin t – t cos t)|