TS Inter 1st Year Maths 1B Solutions Chapter 10 Applications of Derivatives Ex 10(b)

Students must practice this TS Inter 1st Year Maths 1B Study Material Chapter 10 Applications of Derivatives Ex 10(b) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1B Applications of Derivatives Solutions Exercise 10(b)

I.
Question 1.
Find the slope of the tangent to the curve y = 3x⁴ – 4x at x = 4. (V.S.A.Q.)
Answer:
Equation of the given curve is y = 3x⁴ – 4x
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 12x³ – 4
Slope of the tangent at x = 4 is 12(4)³ – 4
= 12(64) – 4
= 764

Question 2.
Find the slope of the tangent to the curve y = \(\frac{x-1}{x-2}\) x ≠ 2 at x = 10. (V.S.A.Q.)
Answer:
Equation of the curve is y = \(\frac{x-1}{x-2}\)
= 1 + \(\frac{1}{x-2}\)
∴ \(\frac{d y}{d x}=-\frac{1}{(x-2)^2}\)
and slope of the tangent at x = 10 is
= \(-\frac{1}{(10-2)^2}=-\frac{1}{64}\)

Question 3.
Find the slope of the tangent to the curve y = x³ – x + 1 at the point whose x coordinate is ‘2’. (V.S.A.Q.)
Answer:
Equation of the curve is y = x³ – x + 1
∴ \(\frac{d y}{d x}\) = 3x² – 1
Slope of the tangent at x = 2 is 3(2)² – 1 = 11

Question 4.
Find the slope of the tangent to the curve y = x³ – 3x + 2 at the point whose x co-ordinate is ‘3’. (V.S.A.Q.)
Answer:
Equation of the curve is y = x³ – 3x + 2
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 3x² – 3
Slope of the tangent at x = 3 is 3 (3)² – 3 = 24

Question 5.
Find the slope of the normal to the curve
x = a cos³θ, y = a sin³θ at θ = \(\frac{\pi}{4}\). (V.S.A.Q.)
Answer:
x = a cos³θ ⇒ \(\frac{d x}{d \theta}\) = 3a cos²θ (-sin θ) dθ
and y = a sin³θ ⇒ \(\frac{d y}{d \theta}\) = 3a sin²θ (cos θ)
\(\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{dy}}{\mathrm{d} \theta} / \frac{\mathrm{dx}}{\mathrm{d} \theta}=\frac{3 \mathrm{a} \sin ^2 \theta \cos \theta}{-3 \mathrm{a} \cos ^2 \theta \sin \theta}\) = – tan θ
∴ Slope of the tangent at θ = \(\frac{\pi}{4}\) is – tan \(\frac{\pi}{4}\) = -1
and hence the slope of the normal = 1.

Question 6.
Find the slope of the normal to the curve x = 1 – a sin θ, y = b cos²θ at θ = \(\frac{\pi}{2}\). (V.S.A.Q.)
Answer:

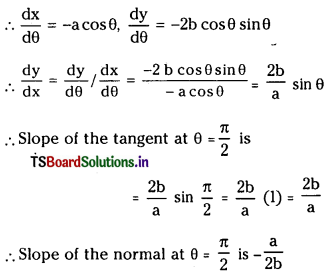
Question 7.
Find the points at which the tangent to the curve y = x³ – 3x² – 9x + 7 Is parallel to the X-axis. (V.SA.Q.)
Answer:
Equation of the curve is y = x³ – 3x² – 9x + 7
∴ \(\frac{d y}{d x}\) = 3x² – 6x – 9

If the tangent is parallel to X – axis then
\(\frac{d y}{d x}\) = 0, ⇒ 3x² – 6x – 9 = 0
⇒ x² – 2x – 3 = 0
x = 3 or – 1
When x = 3, then
y = 3³ – 3(3)² – 9(3) + 7 = – 20
When x = – 1, then y = (- 1)³ – 3(- 1)² – 9 = (-1) + 7 = 12
∴ The required points are (3, – 20), (-1, 12)

Question 8.
Find a point on the curve y = ( x – 2)² at which the tangent is parallel to the chord joining the points (2,0) and (4, 4). (V.S.A.Q.)
Answer:
Equation of the curve is y = (x – 2)²
∴ \(\frac{d y}{d x}\) = 2(x – 2)
Slope of the chord joining points (2, 0) and (4, 4) is = \(\frac{4}{2}\) = 2
The tangent is parallel to the chord 2 (x – 2) = 2
⇒ 2x = 6
⇒ x = 3
y = (x – 2)² = (3 – 2)² = 1
The required point = (3, 1)

Question 9.
Find the point on the curve y = x³ – 11x + 5 at which the tangent is y = x – 11. (V.S.A.Q.)
Answer:
Equation of the curve isy = x³ – 11x + 5
∴ \(\frac{d y}{d x}\) = 3x² – 11
The tangent is y = x – 11
Slope of the tangent is 3x² -11 = 1
⇒ 3x² = 12
⇒ x² = 4
⇒ x = ± 2
y = x – 11, if x = 2 ⇒ y = – 9
The point on the curve is (2, – 9)

Question 10.
Find the equations of all lines having slope zero which are tangents to the curve y = \(\frac{1}{x^2-2 x+3}\) (V.S.A.Q)
Answer:
Equation of the given curve is y = \(\frac{1}{x^2-2 x+3}\)
∴ \(\frac{d y}{d x}=\frac{-1(2 x-2)}{\left(x^2-2 x+3\right)^2}\)
Given slope of the tangent is ‘O’ .
\(\frac{-2(x-1)}{\left(x^2-2 x+3\right)^2}\) = 0 ⇒ x = 1
At x = 1 ⇒ y = \(\frac{1}{1-2+3}=\frac{1}{2}\)
The point is (1, \(\frac{1}{2}\))
Slope of the tangent is ‘0’
∴ Equation of the tangent is
y – \(\frac{1}{2}\) = 0 (x – 1) ⇒ 2y – 1 = 0

II.

Question 1.
Find the equations of tangent and normal to the following curves at the points indicated against. (S.A.Q.)
(i) y = x⁴ – 6x³ + 13x² – 10x + 5 at (0, 5)
Answer:
\(\frac{d y}{d x}\) = 4x³ – 18x² + 26x – 10
At x = 0, slope of the tangent = – 10
∴ Equation of tangent is
y – 5 = – 10 (x – 0) = – 10x
⇒ 10x + y – 5 = 0
Slope of the normal = \(\frac{1}{10}\)
∴ Equation of normal is
y – 5 = \(\frac{1}{10}\)(x – 0) ⇒ 10y – 50 = x
⇒ x – 10y + 50 = 0

(ii) y = x³ at (1, 1)
Answer:
\(\frac{d y}{d x}\) = 3x²
At (1, 1), slope of the tangent = 3 (1)2 = 3
Equation of the tangent at P (1, 1) is
y – 1 = 3 (x – 1)
⇒ 3x – y – 2 = 0
Slope of the normal = –\(\frac{1}{3}\)

∴ Equation of the normal is
y – 1 = –\(\frac{1}{3}\)(x – 1)
⇒ 3y – 3 = -x + 1
⇒ x + 3y – 4 = 0

(iii) y = x² at (0, 0)
Equation of the curve is y = x²
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 2x
At (0, 0) the slope of the tangent is ‘O’ Equation of the tangent is y – 0 = 0 (x – 0)
⇒ y = o
Let equation of normal which is perpendicular to the tangent is of the form x = k
Since the normal passes through (0, 0) we have k = 0
∴ Equation of the normal is x = 0

(iv) x = cos t, y = sin t at t = \(\frac{\pi}{4}\)
Answer:

(v) y = x² – 4x + 2 at (4, 2)
Answer:
Equation of the curve is y = x² – 4x + 2
∴ \(\frac{d y}{d x}\) = 2x – 4
Slope of tangent at (4, 2) is 2(4) – 4 = 4
Equation of the tangent is y – 2 = 4(x – 4)
⇒ 4x – y – 14 = 0
Slope of the normal = \(\frac{-1}{4}\)
∴ Equation of the normal is
y – 2= \(\frac{-1}{4}\)(x – 4)
⇒ 4y – 8 = -x + 4
⇒ x + 4y – 12 = 0

(vi) y = \(\frac{1}{1+x^2}\) at (0, 1)
Answer:
Given equation of the curve is y = \(\frac{1}{1+x^2}\)
∴ \(\frac{d y}{d x}=\frac{-2 x}{\left(1+x^2\right)^2}\)
At (0, 1), slope of the tangent = 0

Equation of the tangent is y – 1 = 0 (x – 0)
⇒ y = 1
Slope of the normal = ∞

∴ Equation of the normal is
y – 1 = \(\frac{1}{0}\) (x – 0)
⇒ x = 0

Question 2.
Find the equations of tangent and normal to the curve xy = 10 at (2, 5). (S.A.Q.)
Answer:
Given equation of the curve is xy = 10
y = \(\frac{10}{x} \Rightarrow \frac{d y}{d x}=\frac{-10}{x^2}\)

Slope of the tangent at the point (2, 5) is \(-\frac{10}{4}=-\frac{5}{2}\)
Equation of the tangent is
y – 5 = \(-\frac{5}{2}\) (x-2)
2y – 10 = -5x + 10
⇒ 5x + 2y – 20 = 0

Slope of the normal is \(\frac{2}{5}\)
∴ Equation of normal at (2, 5) is
y – 5 = \(\frac{2}{5}\)(x – 2)
⇒ 5y – 25 = 2x – 4
⇒ 2x – 5y + 21 = 0

Question 3.
Find the equations of tangent and normal to the curve y = x³ + 4x² at (-1, 3). (S.A.Q.) (May 2014)
Answer:
Equation of the curve is y = x³ + 4x²
∴ \(\frac{d y}{d x}\) = 3x² + 8x
Slope of the tangent at (- 1, 3) is
= 3 (- 1)2 + 8 (- 1) = – 5
Equation of tangent at (- 1, 3) is
y – 3 = – 5 (x + 1)
⇒ 5x + y + 2 = 0

Slope of the normal at (- 1, 3) is \(\frac{1}{5}\)
∴ Equation of normal at (- 1, 3) is
y – 3 = \(\frac{1}{5}\)(x + 1)
⇒ 5y – 15 = x + 1
⇒ x – 5y + 16 = 0

Question 4.
If the slope of the tangent to the curve x² – 2xy + 4y = 0 at a point on it is \(\frac{-3}{2}\), then find the equations of tangent and normal at that point. (S.A.Q.)
Answer:
Equation of the curve is
x² – 2xy + 4y = 0
Differentiating with respect to x

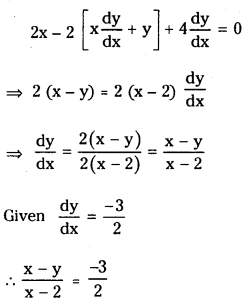
⇒ 2x – 2y = – 3x + 6
⇒ 5x – 2y – 6 = 0 (2)
⇒ 2y = 5x – 6
P (x, y) is a point on the curve and x² – x (5x – 6) + 2 (5x – 6) = 0
⇒ x² – 5x² + 6x + 10x -12 = 0
⇒ -4x² + 16x- 12 = 0
⇒ – 4 (x² – 4x + 3) = 0
⇒ x² – 4x + 3 = 0
⇒ (x – 1) (x – 3) = 0

Case – (i): x = 1, then form (1)
1 – 2y + 4y = 0 ⇒ 2y + 1 = 0 ⇒ y = –\(\frac{1}{2}\)
∴ Required point is P(1, –\(\frac{1}{2}\))

Equation of tangent is
y + \(\frac{1}{2}=\frac{-3}{2}\)(x – 1)
⇒ 2y + 1 = -3x + 3
⇒ 3x + 2y – 2 = 0

Equation of normal is
y + \(\frac{1}{2}=\frac{2}{3}\)(x – 1)
⇒ \(\frac{2 y+1}{2}=\frac{2}{3}\)(x – 1)
⇒ 6y + 3 = 4x – 4
⇒ 4x – 6y – 7 = 0

Case – (ii): When x = 3
∴ From (1); 9 – 6y + 4y = 0
⇒ y = \(\frac{9}{2}\)

Equation of the tangent is
y – \(\frac{9}{2}=\frac{-3}{2}\)(x – 33)
⇒ 2y – 9 = -3x + 9
⇒ 3x + 2y – 18 = 0

Equation of the normal is
y – \(\frac{9}{2}=\frac{2}{3}\)(x – 3)
⇒ \(\frac{2 y-9}{2}=\frac{2}{3}\)(x – 3)
⇒ 6y- 27 = 4x- 12
⇒ 4x – 6y + 15 = 0

Question 5.
If the slope of the tangent to the curve y = x log x at a point on it is \(\frac{3}{2}\), then find the equations of tangent and normal at that point. (S.A.Q.)
Answer:
Equation of the curve is y = x log x
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = x . \(\frac{1}{x}\) + log x = 1 + log x

Question 6.
Find the tangent and normal to the curve y = 2e^-x/3 at the point where the curve meets the Y-axis.
Answer:
Equation of the curve is y = 2e^-x/3
Equation of Y – axis is x = 0 ⇒ y = 2
Required point = (0, 2)
Equation of tangent at P (0, 2) is
y – 2 = \(\frac{-2}{3}\)(x – 0)
⇒ 3y – 6 = – 2x
⇒ 2x + 3y – 6 = 0
Equation of the normal is
y – 2 = y(x – 0)
⇒ 2y – 4 = 3x
⇒ 3x – 2y + 4 = 0

III.

Question 1.
Show that the tangent at P(x₁, y₁) on the curve curved √x + √y = √a is yy₁^{\(\frac{-1}{2}\)} – 2 +xx₁^{\(\frac{-1}{2}\)} = a^{\(\frac{1}{2}\)} (E.Q.) [June 2004]
Answer:
Equation of the curve is √x + √y = √a
Differentiating with respect to x,

Question 2.
At what points on the curve x2 – y2 = 2, the slopes of the tangents are equal to 2 ?(E.Q.)
Answer:
Given equation of the curve
x² – y² = 2 ……….(1)
Differentiating with respect to ‘x’
2x – 2y\(\frac{d y}{d x}\) = 0
⇒ \(\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{x}}{\mathrm{y}}\)

∴ Slope of the tangent at P(x₁, y₁) = 2
Also \(\frac{x_1}{y_1}\) = 2 ⇒ x₁ = 2y₁

Since P(x,, y,) is a point on the curve

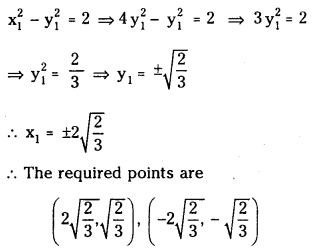
Question 3.
Show that the curves x² + y² = 2 and 3x² + y² = 4x have a common tangent at the point (1, 1). (E.Q.)
Answer:
Equations of the curves are
x² + y² = 2 ……….(1)
3x² + y² = 4x ……(2)
From (1) we have 2x + 2y \(\frac{d y}{d x}\) = 0
⇒ \(\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{-x}{y}\)
Slope of the tangent to the curve (1) at (1, 1) is m₁ = \(\frac{-1}{1}\) = -1

Also from (2), 6x + 2y = 4 dy
⇒ 2y\(\frac{d y}{d x}\) = 4 – 6x
⇒ \(\frac{d y}{d x}=\frac{4-6 x}{2 y}\)

Slope of the tangent to the curve (2) at (1, 1) is m₂ = \(\frac{4-6}{2}=-\frac{2}{2}\) = -1
The slope of the tangents to both the curves at P(1, 1) are same and pass through the same point (1,1).
∴ The given curves have a common tangent at P(1, 1).

Question 4.
At a point (x₁, y₁) on the curve x³ + y³ = 3axy show that the tangent is (x₁² – ay₁)x + (y₁² – ax₁) y = ax₁y₁ (E.Q.)
Answer:
Equation of the curve is x³ + y³ = 3axy
Differentiating w.r. to ‘x’

⇒ y (y₁² – ax₁) – y₁(y₁² – ax₁) = -x(x₁² – ay₁) – x₁(x₁² – ay₁)
⇒ x(x₁² – ay₁) + y(y₁² – ax₁) = -x(x₁² – ay₁) + x₁(x₁² – ay₁)
⇒ x(x₁² – ay₁) +y₁(y₁² – ax₁)
= x₁³ – ax₁y₁ + y₁³ – ax₁y₁
= x₁³ – ax₁y₁ + y₁³ – ax₁y₁
= x₁³ + y₁³ – 2ax₁y₁
= 3ax₁y₁ – 2ax₁y₁
= ax₁y₁
(∵ (x₁, y₁) is a point on the given curve and x₁³ + y₁³ = 3ax₁y₁)

Question 5.
Show that the tangent at the point P(2, – 2) on the curve y(1 – x) = x makes intercepts of equal length on the coordinate axes and the normal at P passes through the origin. (E.Q.)
Answer:
Given equation of the curve is y(1 – x) = x
⇒ y = \(\frac{x}{1-x}\)
∴ Differentiating w.r.t to ‘x’
\(\frac{d y}{d x}=\frac{(1-x)-x(-1)}{(1-x)^2}=\frac{1}{(1-x)^2}\)
At P(2, -2), slope of the tangent = \(\frac{1}{(1-2)^2}\) = 1

Equation of tangent at P(2, – 2) is
y + 2 = 1 (x – 2)
⇒ x – y = 4
⇒ \(\frac{x}{4}+\frac{y}{(-4)}\) = 1 (Intercepts form}
The tangent makes equal intercepts on the co-ordinate axes but they make intercepts with opposite sign.
Equation of normal at P is
y – y₁ = – 1 (x – x₁)
⇒ y + 2 = – 1(x – 2)
⇒ x + y = 0
This passes through the origin.

Question 6.
If the tangpnt at any point on the curve x^2/3+ y^2/3 – a^2/3 intersects the co-ordinate axes in A and B, then show that the length AB is aconstant (E.Q.) [Mar.’14,T3, ’08, ’07, ’05]
Answer:

Equation of the curve is
x^2/3+ y^2/3 = a^2/3 ……………..(1)
Differentiating w.r. to ‘x’

Question 7.
If the tangent at any point P on the curve xm y” = am+“ (mn 5* 0) meets the co-ordinate axes in A and B then show that AP : PB is a constant. (E.Q.)
Answer:
Given curve is x^myⁿ = a^m+n, (mn ≠ 0)
Differentiating with respect to ’x’
x^mny^n-1.\(\frac{d y}{d x}\) + yⁿ. mx^m-1 = 0
⇒ \(\frac{d y}{d x}=-\frac{y^n m x^{m-1}}{x^m n y^{n-1}}=-\frac{m}{n} \cdot \frac{y}{x}\)
Slope of the tangent at (x₁, y₁) = \(\frac{-\mathrm{my}_1}{\mathrm{nx}_1}\)

∴ Equation of the tangent at (x₁, y₁) is
y – y₁ = nx₁ (x – x₁)
⇒ nx₁y – nx₁y₁ = \(\frac{-m y_1}{n x_1}\)mxy₁ + mx₁y₁
⇒ mxy₁ + nx₁y = (m + n) x₁y₁

If P divides AB in the ratio m₁ : m₂ then co-ordinate of P are

∴ Point P divides AB in the ratio n : m and AP : PB = n : m = a constant.