TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(b)

Students must practice these TS Inter 1st Year Maths 1A Study Material Chapter 6 Trigonometric Ratios upto Transformations Ex 6(b) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1A Trigonometric Ratios upto Transformations Solutions Exercise 6(b)

I.
Question 1.
Find the periods for the given 1 – 5 functions.
(i) cos (3x + 5) + 7
Answer:
Let f(x) = cos (3x + 5) + 7
We have period of cos x is 2π ∀ x ∈ R
∴ f (x) is periodic and period of f is = \(\frac{2 \pi}{|3|}=\frac{2 \pi}{3}\)
(or) f (x + p) = f(x)
⇒ cos (3x + 3p + 5) + 7 = cos (2π+ 3x + 5) + 7
3x + 3p + 5 = 2π + 3x + 5
⇒ 3x = 2π
⇒ x = \(\frac{2 \pi}{3}\)

Question 2.
tan x
Answer:
The function tan x is periodic with period π
∴ f(x) = tan 5x is periodic and its period is
\(\frac{\pi}{|5|}=\frac{\pi}{5}\)

Question 3.
cos\(\left(\frac{4 x+9}{5}\right)\) (Mar. ’14)
Answer:
The function f(x) = cos x ∀ x ∈ R has the period 2π
∴ f(x) = cos\(\left(\frac{4 x+9}{5}\right)\) is periodic and period of f is \(\frac{2 \pi}{\frac{4}{5}}=\frac{5 \pi}{2}\)

Question 4.
|sin x|
Answer:
The function sin x has period 2π ∀ x ∈ R
But f(x) = |sin x| is periodic and its period is π
[∵ f(x + π) = |sin(x + π)| = |-sin x| = sinx]

Question 5.
tan (x + 4x + 9x + …. + n²x) (n any positive integer) (March 2015-A.P&T.S)
Answer:
tan [1 + 2² + 3² + ……… + n²) x
= tan\(\left[\frac{\mathrm{n}(\mathrm{n}+1)(2 \mathrm{n}+1)}{6}\right]\)x
Period = \(\frac{6 \pi}{n(n+1)(2 n+1)}\)

Question 6.
Find a sine function whose period is \(\frac{2}{3}\).
Answer:
\(\frac{2 \pi}{\mathrm{k}}=\frac{2}{3}\) ⇒ 3π = |k| ∴ sin kx = sin (3n x)

Question 7.
Find a cosine function whose period is 7. (March 2013)
Answer:
f(x) = cos[\(\frac{2 \pi}{7}\) .x] (\(\frac{2 \pi}{k}\) = 7 ⇒ \(\frac{2 \pi}{7}\) = k)

II. Sketch the graph of the following functions
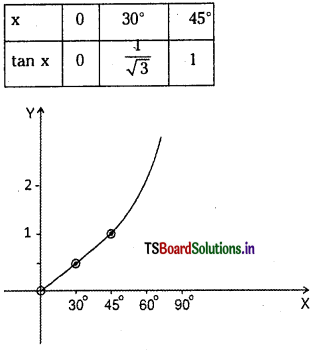
Question 1.
tan x between 0 and \(\frac{\pi}{4}\).
Answer:

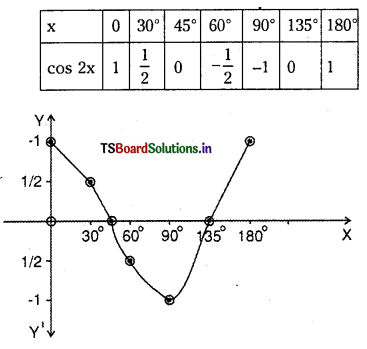
Question 2.
cos 2x in the interval [0, π]
Answer:

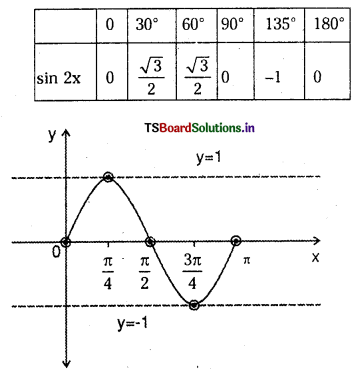
Question 3.
sin 2x in the interval (0, π).
Answer:

Question 4.
sin x in the interval [-π, +π]. (May 2014)
Answer:

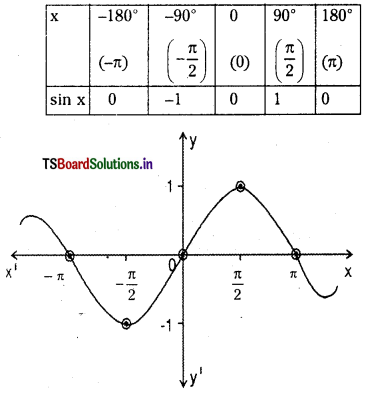
Question 5.
cos²x in [0, π].
Answer:

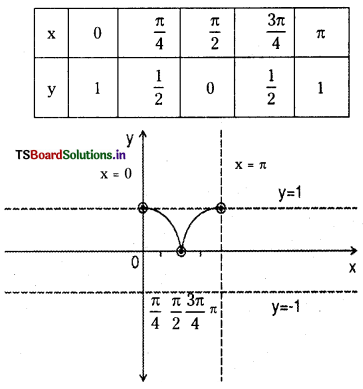
Question 6.
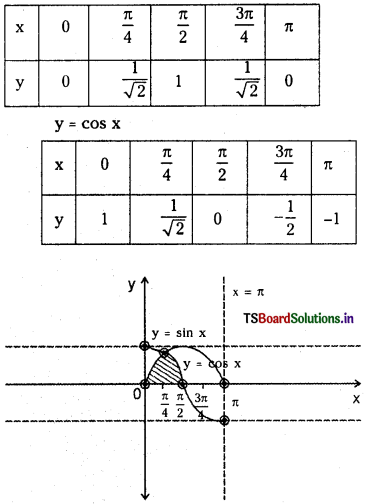
Sketch the region enclosed by y = sin x, y = cos x and X – axis in the interval [0, π].
Answer:
y = sin x