TS Inter 1st Year Maths 1A Solutions Chapter 3 Matrices Ex 3(g)

Students must practice these TS Intermediate Maths 1A Solutions Chapter 3 Matrices Ex 3(g) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1A Matrices Solutions Exercise 3(g)

I.
Examine whether the following systems of equations are consistent or inconsistent and if consistent find the complete solutions,
Question 1.
x + y + z = 4
2x + 5y – 2z = 3
x + 7y – 7z = 5
Answer:
Augmented matrix of the above system is

Rank of the matrix ρ(A) = 2 and ρ(AB) = 3.
Since ρ(A) ≠ ρ(AB), the given system of equa¬tions are inconsistent.

Question 2.
x + y + z = 6
x – y + z = 2
2x – y + 3z = 9
Answer:
Augmented matrix [AB] = \(\left[\begin{array}{rrrr}
1 & 1 & 1 & 6 \\
1 & -1 & 1 & 2 \\
2 & -1 & 3 & 9
\end{array}\right]\)
Apply operations R₂ – R₁, R₃ – 2R₁, we get

Here ρ(A) = 3 and ρ(AB) = 3
Since ρ(A) = ρ(AB), the given system is consistent and has a unique solution.

Question 3.
x + y + z = 1
2x + y + z = 2
x + 2y + 2z = 1 (March 2015-T.S)
Answer:
Augmented matrix of the system is

ρ(AB) = 2 and ρ(A) = 2 and ρ(A) = ρ(AB) < 3
The given system of equations is consis¬tent and has infinitely many solutions.
The given system is equivalent to x + y + z = 1 and y + z = 0.
Solution set is

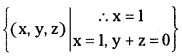
Question 4.
x + y + z = 9
2x + 5y + 7z = 52
2x + y – z = 0
Answer:
Augmented matrix of the system

Here ρ(A) = ρ(AB) = 3; and the system of given equations is consistent; and has a unique solution.
Also x = 1, y = 3, z = 5 form the solution.

Question 5.
x + y + z = 6
x + 2y + 3z = 10
x + 2y + 4z = 1
Answer:
Augmented matrix of the system is

Question 6.
x – 3y – 8z = – 10
3x + y – 4z = 0
2x + 5y + 6z = 13
Answer:
The augmented matrix of the above system is

Since ρ(A) = 2 = ρ(AB) < 3, given system of equations is consistent with infinitely many solutions.
The given system is equivalent to
x – 3y – 8z = – 10,
y + 2z = 3
Put z = t then y = 3 – 2t
∴ x = – 10 + 3(3 – 2t) + 8t
= -10 + 9 – 6t + 8t
= 2t – 1
Hence the solutions are given by
x = 2t – 1, y = 3 – 2t and z = t
Where t is any scalar.

Question 7.
2x + 3y + z = 9
x + 2y + 3z = 6
3x + y + 2z = 8
Answer:
Augmented matrix of the above system is

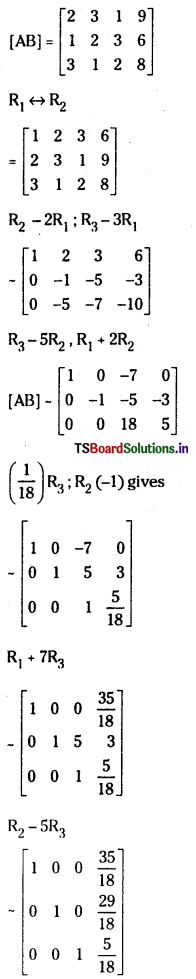
ρ(A) = ρ(AB) = 3; system is consistent and has a unique solution given by
x = \(\frac{35}{18}\), y = \(\frac{29}{18}\), z = \(\frac{5}{18}\)

Question 8.
x + y + 4z = 6
3x + 2y – 2z = 9
5x + y + 2z = 13
Answer:
Augmented matrix of the system

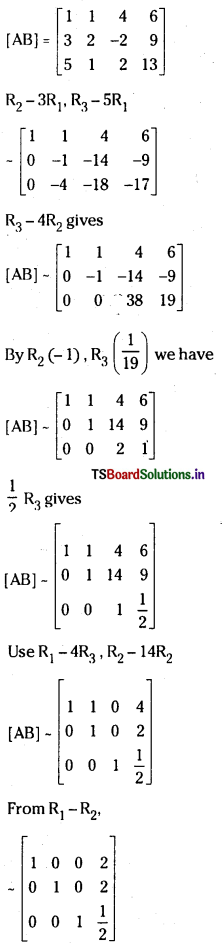
ρ(A) = ρ(AB) = 3;
Hence the system is consistent and has a unique solution given by
x = 2, y = 2, z = \(\frac{1}{2}\).