TS Inter 1st Year Chemistry Study Material Chapter 6 Thermodynamics

Telangana TSBIE TS Inter 1st Year Chemistry Study Material 6th Lesson Thermodynamics Textbook Questions and Answers.

TS Inter 1st Year Chemistry Study Material 6th Lesson Thermodynamics

Very Short Answer Type Questions

Question 1.
What is the information given by the term thermodynamics?
Answer:
The branch of science which deals with the energy transformations such as chemical energy into mechanical energy or the transformation of energies electrical energy, radiant energy, chemical energy and nuclear energy into one another is called thermodynamics.

Question 2.
What is the relationship between the laws of thermodynamics and equilibrium state?
Answer:
Laws of thermodynamics apply only when a system is in equilibrium.

Question 3.
Define a system. Give an example.
Answer:
A small part of the universe that is chosen for thermodynamic study is called system. E.g : water in beaker

Question 4.
The wall is adiabatic and AU = Wad. What do you understand about the heat and work with respect to the system?
Answer:
In the adiabatic system, neither matter nor energy is exchanged with the surroundings. So the wall will not allow the transmission of heat into surroundings or from the surroundings.

Question 5.
The system loses ‘q’ amount of heat though no work is done on the system. What type of wall does the system have?
Answer:
The walls which allow the transmission of heat through them into or out of the system are called diathermal walls.

Question 6.
Work is done by the system and ‘q amount of heat is supplied to the system. What type of system would it be?
Answer:
When q amount of heat is supplied to the system work is done by the system on its surroundings. So it is closed system.

Question 7.
What is the work done in the free expansion of an ideal gas in reversible and irreversible processes?
Answer:
In both cases work done is zero because during free expansion of an ideal gas external pressure becomes zero.

Question 8.
From the equation ∆U = q – p_ex ∆V, if the volume is constant what is the value of ∆U?
Answer:
When volume is constant the amount of heat q supplied increases the internal energy of gas
∆U = q v ∵ ∆V = 0 p_ex ∆V = 0

Question 9.
In isothermal free expansion of an ideal gas find the value of q and ∆U.
Answer:
∆U = 0, q = 0, since W = 0 l P_ext = 0

Question 10.
In isothermal irreversible change of ideal gas what is the value of q?
Answer:
For isothermal irreversible change
q = – W = p_ex (V_f – V_i)

Question 11.
In isothermal reversible change of an ideal gas, what is the value of q?
Answer:
q = – W = 2.303 nRT log \(\frac{V_f}{V_i}\)

Questin 12.
For an adiabatic change in an ideal gas what is the relationship between its AU and W (adiabatic)?
Answer:
For adiabatic change, q = 0 ; AU = Wad

Question 13.
State the first law of the thermodynamics. [Mar. ’18 (TS) (AP ’16)]
Answer:
Energy can neither be created nor be destroyed.

Question 14.
What are the sign conventions of the work done on the system and work done by the system?
Answer:
When work is done on the system it is represented with + ve sign while work done by the system is given with – ve sign.
Work done by the system = – ve
Work done on the system = + ve.

Question 15.
Volume (V), Pressure (P) and Temperature (T) are state functions. Is the statement true?
Answer:
Yes, it is true. Volume (V), Pressure (P) and Temperature (T) are state functions and depend only on the initial and final states.

Question 16.
What are the heat (q) sign conventions when heat is transferred from the surroundings to the system and that transferred from system to the surrounding?
Answer:
When heat is transferred from surroundings to the system its internal energy increases. So it is represented with + ve sign.

When heat is transferred from system to surroundings the internal energy of the system decreases. So it is represented with – ve sign.

Question 17.
No heat is absorbed by the system from the surroundings, but work (w) is done on the system. What type of wall does the system have?
Answer:
Adiabatic wall

Question 18.
No work is done on the system, but heat (q) is taken out from the system by the surroundings. What type of wall does the system have?
Answer:
The walls which allow the transmission of heat through them into or out of the system are called diathermal walls. So the system has diathermal walls.

Question 19.
Work is done by the system and heat (q) is supplied to the system. What type of system would it be?
Answer:
∆U = q-W (or) ∆U = q – P^ext ∆V, closed system.

Question 20.
q = w = – P_ext (υ_f – υ_i) is for irreversible ……….. change.
Answer:
Isothermal.

Question 21.
q = – w = nRT In (vf- vt) is for isothermal change.
Answer:
Reversible.

Question 22.
What are the ‘∆H’ sign conventions for exothermic and endothermic reactions? [TS ’16]
Answer:
For exothermic reaction, ∆H = – ve
For endothermic reaction, ∆H = + ve

Question 23.
What are intensive and extensive properties? [AP Mar. ’19; (AP ’15)]
Answer:
Measurable properties of a system may be classified into two types
i) extensive properties
ii) intensive properties.

i) Extensive Properties :
The properties of a system which depend on the total amount of the material present in the system are called extensive properties.
Examples:
Mass (m), volume (V), internal energy (E), heat content (H), gibbs energy (G), entropy (s), heat (v) capacity, etc. are extensive properties.

ii) Intensive properties :
Properties of a system which are independent of the amount of the material in the system are called intensive properties.
Examples :
Density, molar properties such as molar volume, molar entropy, molar heat capacity, surface tension(S), viscosity, specific heat, refractive index, pressure, temperature, boiling point, freezing point and vapour pressure are intensive properties.

Question 24.
In the equation q = C.m – ∆T, if ∆T is change in temperature ‘m’ mass of the substance, and ‘q’ is heat required, what is ‘C’?
Answer:
C is the heat capacity.

Question 25.
Give the equation that gives the relation-ship between ∆U and ∆H.
Answer:
∆H = ∆U + ∆nRT
∆H = enthalpy change
∆U = change in internal energy
∆n = change in no.of moles
R = Universal gas constant
T = Temperature

Question 26.
What is the relationship between C_p and C_v?
Answer:
C_P = C_V + R or C_P – C_V = R
C_P = Heat capacity at constant pressure
C_V = Heat capacity at constant volume
R = Universal gas constant

Question 27.
1 g of graphite is burnt in a bomb calorimeter in excess of Oz at 298 K and 1 atm. pressure according to the equation.
C_(graphite) + O_{2 (g)} → CO_{2 (g)}
During the reaction the temperature rises from 298 K to 299 K. Heat capacity of the bomb calorimeter is 20.7 kJK^-1. What is the enthalpy change for the above reaction at 298 K and 1 atm?
Answer:
Heat absorbed by calorimeter = C_V ∆T
= (20.7 kJ k^-1) × 1 = 20.7 kJ
Heat evolved during combustion of 1 gm of graphite = – 20.7 kJ
∆_cH^θ = \(\frac{-20.7\times12}{1}\) = 248.4kJ

Question 28.
For the above reaction what is the inter-nal energy change, ∆U?
Answer:
∆H = ∆U + p∆V
Since the volume of the bomb calorimeter is constant ∆H = ∆U. i.e., 20.7 kJ.

Question 29.
What is ∆_rH for
CH_4(g) + 2O_2(g) → CO_2(g) + 2H₂O_(l)
in terms of molar enthalpies of the respective reactants and products?
Answer:
∆_rH = ∑molar enthalpies of products – ∑molar enthalpies of reactants.
The molar enthalpies of the elements in the standard state are taken as zero.
∴ ∆_rH = ∑molar enthalpy of CO₂ and H₂O – molar enthalpy of CH₄.

Question 30.
Enthalpy decrease is not the criterion for spontaneity. Why?
Answer:
For the spontaneity of a reaction ∆G must be negative. Though the enthalpy increases if T∆S is more negative then ∆G becomes negative in the equation
∆G = ∆H – T∆S

So decrease in enthalpy is not a criterion for the spontaneity of the reaction.

Question 31.
Is increase of entropy the criterion for spontaneity? Why?
Answer:
No. For the spontaneity of the reaction, ∆G must be negative. Even though entropy does not increase if the ∆H is more negative than T∆S in the equation ∆G = ∆H – TAS, ∆G becomes negative and the reaction becomes spontaneous.

Question 32.
Explain the relationship between Gibbs energy change and equilibrium constant.
Answer:
Gibbs energy ∆_rG^θ is related to the equilibrium constant of the reaction as follows.
O = ∆_rG^θ + RT In K
or ∆_rG^θ = – RT /n K
or ∆_rG^θ = – 2.303 RT log K.

Question 33.
If we measure AH^θ and AS^θ it is possible to estimate AG^θ. Is it true? Why?
Answer:
Gibbs Helmholtz equation is ∆G^θ = ∆H^θ – T∆S^θ Standard values of ∆H^θ, ∆S^θ and ∆G^θ are measured at standard temperature 298 K. So, if we measure ∆H^θ and ∆S^θ it is possible to estimate ∆G^θ according to the above relation.

Question 34.
Equilibrium constant ‘K’ is measured accurately in the laboratory at given temperature. Is it possible to calculate ∆G^θ at any other temperature? How?
Answer:
Gibbs energy for a reaction ∆G^θ is related to equilibrium constant of the reaction as follows.
O = ∆_rG^θ + RT ln K
or ∆_rG^θ = – RT ln K
or ∆_rG^θ = -2.303 RT log K.

If k_x is measured, the value of ∆_rG^θ at any temperature can be calculated. By substituting the k_x value at a different temperature T_x we can calculate ∆G^θ at that temperature
∆_rG^θ = – 2.303 RT_x log K_x

Question 35.
Comment on the thermodynamic stability of NO_(g) given that
\(\frac{1}{2}\)N_2(g) + \(\frac{1}{2}\)O_2(g) → NO_(g); ∆_rH^θ = 90kJmol^-1
NO_(g) + \(\frac{1}{2}\)O_2(g) → NO_2(g); ∆_rH^θ = -74 kJmol^-1
Answer:
Exothermic compounds are stable while endothermic compounds are unstable.
NO is endothermic compound so unstable.
NO₂ is exothermic compound so stable.

Question 36.
Calculate the entropy change in surroundings when 1.00 mole of H₂O(l) is formed under standard conditions
∆_fH^θ= -286 kJmol^-1.
Answer:

Question 37.
The equilibrium constant for a reaction is 10. What will be the value of ∆H^θ?
R = 8.314 JK^-1mol^-1, T = 300 K.
Answer:
∆H^θ =-2.303 RT log k
= – 2.303 × 8.314 Jk^-1 × 300 k × log 10
= – 2.303 × 8.314 Jk^-1 × 300 k × 1
= – 5.744 kJ

Question 38.
State the third law of thermodynamics. [AP Mar. ’19; (TS ’16)]
Answer:
At absolute zero the entropy of any pure crystalline sybstance approaches zero.

Short Answer Questions

Question 1.
What are open, closed and isolated systems? Give one example for each.
Answer:
Types of systems :
Basing on the fact that whether energy or matter or both are exchanging between the system and the surroundings the systems are classified into three types, a) open system b) closed system c) isolated system.

a) Open system :
A system which can exchange both matter and energy with its surroundings is called open system.
Ex : A liquid in an open vessel. It can absorb heat energy from the surroundings and can give heat energy to the surroundings during evaporation and condensation. Similarly water can go as vapour into the surroundings and vapour can condense as liquid into the beaker.

b) Closed system :
A system which can exchange energy but not matter with its surroundings is called closed system.
Ex: Water taken in a closed non porous vessel. This can take heat from the surroundings and is evaporated. The vapour can condense back into liquid releasing heat to the surroundings. But water cannot leave or enter the vessel because it is closed.

c) Isolated system:
A system in which neither matter nor energy is exchanged with surroundings.
Ex : Liquid taken in a closed thermos flask. Heat can neither enter nor leave the flask. Similarly liquid or its vapour cannot go into the surroundings.

Question 40.
Define the state function and state variables. Give examples.
Answer:
The thermodynamic properties whose values depend only on the initial and fihal state of the system and are independent of matter or the manner as to how the change is brought about are called state functions.

In thermodynamics, some common state functions are internal energy (U), enthalpy (H), entropy (S), Gibbs energy (G), pressure (P), temperature (T), volume (V) etc.

Variables such as P, V, T are called state variables. These are used to describe the system completely.

Question 2.
“Internal energy is a state function.” Explain.
Answer:
If some mechanical work of about 1 kJ is carried by rotating a set of small paddles and thereby churning water, heat is produced. Thus the temperature increases. The new state of system B may have temperature T_b‘. This state of system is brought from a state A at a temperature T_A. If the internal energy of system in the state A is U_A and in the state B is U_B, the change in internal energy ∆U = U_B – U_A.

In another way the system in the state A can be brought to the state B by dipping a hot rod into water which supply same amount of energy 1 kJ. Then we find the change in temperature is same as in the first case say T_B – T_A.

This shows that a given amount of work done irrespective of path produced the same change of state.

The internal energy U is characteristic of the state of the system. The adiabatic work W_ad required to bring about a change of state is equal to the difference between the value of U in one state and that in another state ∆U.
∆U = U₂ – U₁ = W_ad

Therefore internal energy U of the system is a state function.

Question 3.
“Work is not a state function.” Explain.
Answer:
A change of state is brought about both by doing work and by transfer of heat. The change in internal energy for this case as
∆U = q + w

For a given change in state q and w vary depending on how the change is carried out. However q + w = ∆U depend only on the initial and final state. It will be independent of the way the change is carried out.

Thus work and heat depend on the path in which the state changes. So work is not state function but path function.

Question 4.
What is heat? Explain.
Answer:
Heat is a form of energy.

Consider two identical balls of iron, one at 50°C and the other at 100°C. Of these one is hotter than the other. The relation between heat and work is
W = J . Q.

where ‘J’ is a constant known as the mechanical equivalent of heat. W = Work done, Q = Heat liberated. The value of J is 4.8 × 10⁷ ergs/calorie. In the C.G.S system mechanical work is measured in units of erg. Heat is measured in units of calorie. Thus 4.18 × 10⁷ ergs of work must be done to produce one calorie of heat.

Question 5.
Derive the equation for ‘Wrev’ in isothermal reversible process.
Answer:
Work done during the expansion of a gas against external pressure can be expressed as
W = P_ext(-∆V) = -P_ext(V_f – V_i)
In isothermal reversible process the above equation can be written as

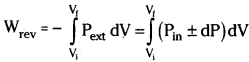
Since d_P × d_V is very small it can be neglected and we can write the equation as

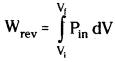
Now the pressure of the gas P_in can be written as P.

This can be obtained from ideal gas equation.
P = \(\frac{nRT}{V}\)
Therefore at constant temperature (isothermal process)

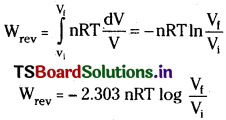
Question 6.
Two litres of an ideal gas at a pressure of 10 atm expands isothermally into a vacuum until its total volume is 20 litres. How much heat is absorbed and how much work is done in the expansion?
Answer:
Pressure of the gas 10 atm.
q = – W = P∆V
Since the gas expands into vacuum the pressure, P = 0
∴ q = -W = 0(20-2) = 0
∴ Heat change and work done are zero.

Question 7.
If the ideal gas given in the problem 45 expands against constant external pressure of 1 atm what is the q value?
Answer:
q = – W = P∆V = 1 (20 – 2) = 18 L atm.

Question 8.
If the ideal gas given in the problem 45 expands to a final volume of 10 L con-ducted reversibly what is q value?
Answer:
V₁ = 2 lit, V₂ = 10 lit
In the reversible isothermal expansion,
q = – W
∴ q = – W = 2.303 log \(\frac{20}{2}\) = 2.303 × log 10
= 46.06 lit. atm.

Question 9.
Explain the state function ‘enthalpy, H’. What is the relationship between ∆U and ∆H?
Answer:
The heat absorbed at constant volume is equal to change in the internal energy ∆U = q_v. But in the heat absorbed at constant pressure, a part of it increases the internal energy ∆U and the remaining part is used in the expansion work done by the system. If the initial state is represented with a subscript 1 and the final state with a subscript 2. Then the above equation can be written as
U₂ – U₁ = q_p – p (V₂ – V₁)
or q_p = (U₂ + pV₂) – (U₁ + pV₁)
The value of U + pV is called enthalpy and represented by H. So enthalpy,
H = U + pV
q_p = H₂ – H₁ = ∆H

Though ‘q’ is path function, H is a state function because it depends on U, p and V, all of which are state functions.
Therefore ∆H is independent of path.
The relation between ∆U and ∆H is
∆H = ∆U + p∆V (∵ p∆V = W)

Question 10.
Show that ∆H = ∆U + ∆n_(g), RT
Answer:
When the reaction takes place between solids or liquids pressure has no effect. With change in temperature since the volume change of solids or liquids is negligible with temperature is negligible. But in the reactions involving gaseous substances there is significant difference in ∆H and ∆U.

If V_A is the total volume of the gaseous reactants V_B is the total volume of the gaseous products, n_A is the number of moles of gaseous reactants and n_B is the number of moles of gaseous products, all at constant pressure and temperature, then using ideal gas law,
pV_A = n_ART
and pV_B = n_BRT
Thus, pV_B – pV_A = n_BRT – n_ART
or pV_B – pV_A = (n_B – n_A)RT
P(V_B – V_A = (n_B – n_A) RT
or p∆V = An_gRT

Here, ∆n_g is number of moles of gaseous products – number of moles of gas-eous reactants.
Substituting the value of p∆V in f
∆H = ∆U + p∆V
We get, ∆H = ∆U + ∆n_gRT

Question 11.
If water vapour is assumed to be a perfect gas, molar enthalpy change for vapouration of 1 mole of water at 1 bar and 100°C is 41 kJ mol^-1. Calculate the internal energy change when
a) 1 mol of water is vapourised at 1 bar and 100°C
b) 1 mol of water liquid is converted into ice.
Answer:
a) H₂O(1) → H₂O(g)
∆n = 1
∆H = ∆U + ∆n_gRT
41 = ∆U + (1 × 8.314 × 10^-3 × 373)
∆E = 41 – 3.1 = 37.9 kJ.

∆n = 0
∆H = ∆U + ∆n_gRT
∴ ∆H = AU (∵ n_gRT = 0)
So, ∆U = 41

Question 12.
Explain extensive and intensive properties.
Answer:
Measurable properties of a system may be classified into two types
i) extensive properties
ii) intensive properties.

i) Extensive Properties :
The properties of a system which depend on the total amount of the material present in the system are called extensive properties.
Examples:
Mass (m), volume (V), internal energy (E), heat content (H), gibbs energy (G), entropy (s), heat (v) capacity, etc. are extensive properties.

ii) Intensive properties :
Properties of a system which are independent of the amount of the material in the system are called intensive properties.
Examples :
Density, molar properties such as molar volume, molar entropy, molar heat capacity, surface tension(S), viscosity, specific heat, refractive ipdepf, pressure, temperature, boiling point, freezing point and vapour pressure are intensive properties.

Question 13.
Define heat capacity. What are C_p and C_v? Show that C_p – C_v = R.
Answer:
Heat capacity of a substance is defined as the amount of heat required to raise its temperature through one degree.

The heat capacity at constant volume is represented by C_v. C_v gives the measure of the change of internal energy (E) of a system with temperature.

If heat is absorbed by the system at a constant pressure, heat capacity is represented by C_p. It is called heat capacity at constant pressure.

At constant pressure when heat is absorbed the volume of the gas increase. While the gas expands it does some work, for which extra heat amount is required. Hence C_p always greater than C_V. The C_p is equal to change in internal energy and the work done. The work done is equal to PV where V is the change in volume.

Relation between C_P and C_V:
For an ideal gas H = E + PV

Differentiating with temperature
\(\frac{dH}{dT}=\frac{dE}{dT}+\frac{d(PV)}{dT}\)
For one mole of ideal gas PV = RT

Question 14.
Explain the determination of ∆U of a reaction calorimetrieally.
Answer:
The change in internal energy ∆U in a chemical reaction can be determined using bomb calorimeter. The bomb is a steel vessel. It is immersed in a water bath. The whole device is called calorimeter.

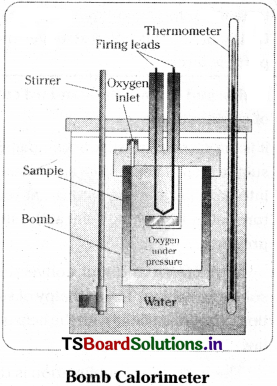
A combustible substance is burnt in pure oxygen supplied in the steel bomb. The heat evolved during the reaction measured from the rise in the temperature. Since the bomb calorimeter is sealed, the energy changes taking place in it are considered as that taking place at constant volume. Temperature change of the calorimeter produced by the reaction is then converted to qv by using the known heat capacity of the calorimeter.
q = – C × \(\frac{M}{W}\) × ∆T
where C’ is the heat capacity of calorimeter
∆T is the change in temperature
W is the mass of substance
M is the molecular mass of substance taken.

Question 15.
Explain the determination of ∆H of a reaction calorimetrieally.
Answer:
The change of enthalpy ∆H of a reaction can be measured in a calorimeter as shown in the figure. However the calorimeter is kept open to the atmosphere.

The calorimeter is immersed in an insulated water bath fitted with stirrer and thermometer. The temperature of the bath is recorded in the beginning and after the end of the reaction and change in temperature is recorded. Knowing the heat capacity of water bath and calorimeter and also the change in temperature, the heat absorbed or evolved in the reaction can be calculated. This gives the enthalpy change (∆H) of the reaction.

Question 16.
What is enthalpy of a reaction? Explain the standard enthalpy of a reaction.
Answer:
The enthalpy of a reaction is defined as the enthalpy change accompanying the chemical reaction when the molar quantities of reactants and products are the same as indicated in the chemical equation. It is also known as heat of reaction. It is represent id by ∆H.

The enthalpy change at the standard state conditions is called standard enthalpy of the reaction. It is denoted by ∆_rH^θ. The superscript (θ) represents standard state.

Standard state of a substance is its most stable state at one bar pressure and 298 k.

Question 17.
What is the standard enthalpy of formation? Explain it with example.
Answer:
Standard heat of formation of a compound is defined as the heat change accompanying the formation of one mole of a compound from its constituent elements, all the substances being in their standard states (1 bar pressure and 298 k).

Standard enthalpy of formation of the substance is also called its standard enthalpy and denoted by H^θ. Standard enthalpies of free elements are taken to be zero e.g.

C_(graphite) + O₂(g) → CO₂(g); ∆H^θ = – 393,5 kJ

Question 18.
Define and explain enthalpy of phase transformation.
Answer:
The conversion of solid to liquid is called melting or fusion and the process of conversion of liquid into gas is called vapourisation. These processes are collectively called phase transformations or phase changes.

The enthalpy change accompanying the conversion of 1 mole of a solid substance into the liquid state at its melting point is called enthalpy of fusion.

The enthalpy change accompanying the conversion of one mole of a liquid into its vapours at the boiling is called enthalpy of vapourisation.

Question 19.
Define and explain the standard enthalpy of fusion (Molar enthalpy of fusion).
Answer:
The enthalpy change accompanying the conversion of 1 mole of a solid substance into the liquid at its melting point is called the standard enthalpy of fusion.

The standard enthalpy of fusion of a substance depends largely on the strength of intermolecular forces in the substance undergoing fusion. For example ionic solids have very strong interparticle forces. Such substances have high values of enthalpy of fusion. Molecular solids have weak interparticle forces. They have low enthalpy values of fusion.

Question 20.
Define and explain the standard enthalpy of vapourisation (Molar enthalpy of vapourisation).
Answer:
The enthalpy change accompanying the conversion of one mole of a liquid into its vapours at its boiling point is called standard molar enthalpy of vapourisation.

The values of enthalpy of vapourisation give some idea about the magnitude of interparticle forces in liquids. More the enthalpy of vapourisation stronger the inter particle forces.

Question 21.
Define and explain the standard enthalpy of sublimation.
Answer:
It is the enthalpy change accompanying the sublimation of one mole of a solid substance into gaseous state at a constant temperature below its melting point at the standard pressure.

Sublimation is direct conversion of a solid into vapour. The enthalpy of sublimation can be calculated with the help of Hess’s law.

The enthalpy of sublimation is the sum of enthalpy of fusion and enthalpy of vapourisation
∆_subH = ∆_fusH + ∆_vapH

Question 22.
Define and explain the standard enthalpy of formation (∆_fH^θ).
Answer:
The enthalpy of formation is the heat change accompanying the formation of one mole of a compound from its constituent elements. It is generally denoted by ∆_fH. For example the enthalpy of formation of carbondioxide can be represented as
C_(graphite) + O_2(g) → CO_2(g) ; ∆H = – 396.5 kJ

When all the species of the chemical reaction are in their standard states, the enthalpy of formation is called standard heat of formation. It is denoted by ∆H^θ.

The standard heat of formation is defined as the heat change accompanying the formation of one mole of a compound from its constituent elements all the substances being in their standard states (1 bar pressure and 298 k).

Question 23.
State and explain the Hess’s law of constant heat summation. [Mar. ’18(AP&TS) AP ’17, ’16, ’15, ; TS ’16, ’15; Mar. ’13]
Answer:
Hess’s law :
Energy changes remains constant whether the reactions takes place in single step or in several steps. [TS Mar. ’19]

I. Formation of CO₂ : CO₂ can be formed either in one step or in two steps.
a) C_(graphite) + O₂ (g) → CO₂ (g), ∆H = – 393.5 kJ
b) C_(graphite) + \(\frac{1}{2}\)O₂ (g) → CO (g), ∆H = -110.5 kJ
CO (g) + \(\frac{1}{2}\)O₂(g) → CO₂(g),
∆H = – 283.5 kJ ,
Total ∆H = – 393.52 kJ

Reaction ‘a’ is completed in single step and reaction ‘b’ is completed in two steps. But in both the cases energy changes remain constant, which proves Hess’s law.

II. Formation of NH₄Cl (aq) :
a) NH₃ (g) + H₂O (l) → NH₃ (aq), ∆H = – 35.1 kJ
HCl (g) + H₂O (l) → HCl (aq), ∆H = – 72.9 kJ
NH₃ (aq) + HCl (aq) → NH₄Cl (aq), ∆H = -51.5 kJ
Total ∆H = – 159.5 kJ

b) NH₃(g) + HCl (g) → NH₄Cl (g), ∆H = -176.1 kJ
NH₄Cl (S) + H₂O (l) → NH₄Cl (aq), ∆H = + 16.3 kJ .
Total ∆H = – 159.8 kJ

In both reactions (a) and (b), the heat of formation of NH₄Cl (aq.) is the same, which proves Hess’s law.

Uses of Hess’s law: It is used to determine

1. Heat of formation.
2. Heat of reaction.
3. Crystal lattice energy.
4. Transition temperatures of allotropic forms.

Question 24.
Define and explain the enthalpy of combustion (∆_cH^θ).
Answer:
It is the enthalpy change accompanying the complete combustion of one mole of a substance in excess of oxygen or air.

For example, the enthalpy of combustion of carbon is represented as
C_(s) + O₂ (g) → CO_2(g) ; ∆H = -393.5 kJ

Combustion reactions are always accompanied by the evolution of heat, therefore, the value of ∆_cH is always negative.

Question 25.
Define and explain the enthalpy of atomisation (∆_cH^θ).
Answer:
It is the enthalpy change on breaking one mole of bonds completely to obtain neutral atoms in the gas phase.

In case of diatomic molecules, like H₂, HCl etc., the enthalpy of atomisation is also the bond dissociation enthalpy. In the case of metals enthalpy of atomisation is the enthalpy of sublimation.

Question 26.
Define and explain the bond enthalpy (∆_bondH^θ).
Answer:
The bond dissociation enthalpy is the change in enthalpy when one mole of covalent bonds of a gaseous covalent compound is broken to form products in the gas phase.

In the case of diatomic molecules like H₂, HCl etc., the enthalpy of atomisation is also the bond dissociation enthalpy. In the case of polyatomic molecules, bond dissociation enthalpy is different for different bonds within the same molecule.

Question 27.
What is the bond enthalpy of C-H bond of CH₄?
Answer:
The overall thermochemical equation for its atomisation reaction is
CH_{4 (g)} → C_(g) – 4H_(g) ; ∆_aH^θ = 1665 Id mol^-1

In methane, all the four C-H bonds are similar in bond length and energy. However the energies required to break the individual C – H bonds in each successive step differ.
CH_4(g) → CH_3(g) +H_(g); ∆_bondH^θ = +427 kJmol^-1
CH_3(g) → CH_2(g) + H_(g); ∆_bondH^θ = +439kJmol^-1
CH_2(g) → CH_(g) + H_(g); ∆_bondH^θ = +452kJmol^-1
CH_(g) → C_(g) + H_(g); ∆_bondH^θ = +347kJmol^-1
Therefore,
CH_4(g) → C_(g) + 4H_(g); ∆_aH^θ = 1665 kJmol^-1

In such cases we use mean bond enthalpy of C-H bond.
So in CH₄ ∆_C-HH^θ is 1665 kJmol^-1/4
= 416 kJ mol^-1

Question 28.
Define heat of solution (∆_solH^θ) and heat of dilution.
Answer:
Enthalpy of solution of a substance is the enthalpy change when one mole of it dissolves in a specified amount of solvent.

Enthalpy change associated with the addition of a specified amount of solute for the specified amount of solvent at a constant temperature and pressure is known as the enthalpy of dilution.

Question 29.
Define ionisation enthalpy and electron affinity.
Answer:
Ionisation enthalpy is the energy required to remove an electron from an isolated gaseous atom in its ground state.
X_(g) → X⁺_4(g) + e^–

The ionisation enthalpy is expressed in units kJ mol^-1.

The enthalpy change accompanying the process of conversion of a neutral gaseous atom into negative ion by adding an electron is called electron gain enthalpy.
X_(g) + e^– → X^–_(g)

The electron gain enthalpy is also known as electron affinity of the atom under consideration.

Question 30.
Explain the spontaneity of a process.
Answer:
The process which takes place on its accord without the aid of an external agency is called spontaneous process.
Ex : (1) Heat flows from hot end to cold end (2) Water flows from higher level to lower level.

Spontaneous process is an irreversible process and may only be reversed by some external agency. In general for a spontaneous reaction ∆H is +ve. But for a spontaneous reaction ∆G must be -ve. All natural processes are spontaneous.

Question 31.
Is decrease in enthalpy a criterion for spontaneity? Explain.
Answer:
For the spontaneity of a reaction AG must be negative. Though the enthalpy increases if T∆S is more negative then AG becomes negative in the equation
∆G = ∆H – T∆S

So decrease in enthalpy is not a crite-rion for the spontaneity of the reaction.

Question 32.
What is entropy? Explain with examples.
Answer:
Entropy :
Entropy means transformation. It is denoted by ‘S’.

Entropy is a measure of disorder or randomness in a system.

The greater the disorder in a system the higher is the entropy. Entropy is a state function. Entropy change (∆S) between any two states is therefore given by the equation.
∆S = \(\frac{q_{rev}}{T}\)

q_rev is the heat absorbed by the system isothermally and reversibly at T during the state change.

A substance in solid state have lowest entropy because the particles are orderly arranged. The gaseous state of the same substance have highest entropy because the particles are moving most disorderly. The liquid state of the same substance have entropy in between the values for solid and the gaseous state.

For a spontaneous process in an isolated system the change in entropy (∆S) is positive.

Question 33.
Is increase in entropy a criterion for spontaneity? Explain.
Answer:
No. For the spontaneity of the reaction ∆G must be negative. Even though entropy does not increase if the ∆H is more negative than T∆S in the equation ∆G = ∆H – T∆S, AG becomes negative and the reaction be-comes spontaneous.

Question 34.
Can ∆U and AS discriminate between irreversible and reversible processes? Explain.
Answer:
AU does not discriminate between irreversible and reversible process. For isothermal process involving ideal gas T is constant. Hence ∆U = 0 for both reversible and irreversible process.

∆S discriminates the irreversible and reversible process.

In an isothermal reversible process if the amount of heat Q is absorbed from the surroundings at a temperature T, the increase in the entropy of the system will be
∆_sys = + \(\frac{Q}{T}\)

On the other hand surroundings lose the same amount of heat at the same temperature. The decrease in entropy of the surroundings will

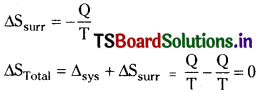
In the irreversible process the system is at higher temperature T₁ and its surroundings at lower temperature T₂. ‘Q’ amount of heat goes irreversibly from system to surroundings

Hence entropy increases in an irreversible process.

Question 35.
In which of the following processes entropy increases?
a) A liquid evaporates to vapour.
b) Temperature of a crystalline solid lowered from 115 K to 0 K.
c) CaCO_3(s) → CaO_(s) + CO_2(g)
d) Cl_3(g) → 2Cl_(g)
Answer:
a) A liquid evaporates vapour:
During the vapourisation, the liquid absorbs heat at constant temperature. In this process the liquid state converts into gaseous state. In the liquid state the particles are close to one another and somewhat the order of the particles is more. In gaseous state the order of the particles is less and disorder increases due to the random motion of gaseous particles. So entropy increases during the vapourisation of a liquid.

b) Temperature of a crystalline solid lowered from 115K to OK:
Ina crystalline solid the particles are arranged in an orderly maimer. Due to decrease in temperature there will be no change in the order but due to decrease in vibrational energies the entropy decreases.

c) CaCO_3(s) → CaO_(s) + CO_2(g):
Here one of the product is gas in which randomness increases than in the solid reactant. So entropy increases.

d) Cl_2(g) → 2Cl_(g):
Here both are gases but one Cl₂ molecule converts into 2 Cl atoms due to which randomness increases. So entropy increases.

Question 36.
For the oxidation of iron
4Fe_(s) + 3O_2(g) → 2Fe₍₂₎O_3(s),
the entropy change is – 549.45 JK^-1 mol^-1 at 298 K. Though it has negative entropy change the reaction is spontaneous. Why? (∆_rH^θ = – 1648 × 10³ J ml^-1)
Answer:
∆G = ∆H – T∆S
= 1648 × 10³ J mol^-1 – 298 (-549.45)
= 1648 × 10³ + 163 × 10³ = – 1485 × 10³
∆G is negative.
Since ∆G is negative, though entropy change is negative the reaction takes place spontaneously.

Question 37.
Which formulae in the following are correct?

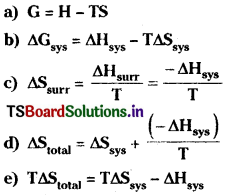
Answer:
a) Correct.
b) Correct.
c) Correct.
d) Correct.
e) Correct.

Question 38.
Calculate ∆_rH^θ for conversion of oxygen to ozone \(\frac{3}{2}\)O_2(g) → O_3(g) at 298 K. K_p for the reaction is 2.43 × 10^-29
Answer:
∆_rG^θ = -2.303 RT log K_p
K_p = 2.43 × 10^-29
∆_rG^θ = – 2.303 × 8.314 × 298 (log 2.43 × 10^-24)
∆_rG^θ = 163 kJ

Question 39.
State the second law of thermodynamics and explain it.
Answer:
Second law of thermodynamics may be stated as
Heat cannot flow from a colder body to a hotter body on its own.
(or)

Heat cannot be converted into work completely without causing some permanent changes in the system involved or in the surroundings.
(or)
All spontaneous processes are thermodynamically irreversible and entropy of the system increases in all spontaneous processes.
(or)
It is impossible to construct a machine which is working in cycles that can transform heat from lower temperature to higher temperature without the help of an external agency.

Second law of thermodynamics is useful in predicting

1. Whether a process occurs in a specified direction or not on its own without the intervention of any external agency i.e., whether a process is spontaneous or not in the specified direction.
2. If a transformation or a process occurs, what fraction of one form of energy is converted into another form of energy in this transformation or process.
3. A machine which transfers heat from lower temperature to higher temperature on its own is called perpetual motion machine of second
   kind. Second law of thermodynamics predicts that perpetual motion machine is not possible.

Question 40.
State the third law of thermodynamics. What do you understand by it?
Answer:
Third law of Thermodynamics :
The entropy of a pure and perfectly crystalline substance is zero at the absolute zero temperature (- 273°C).
S_lim T → 0 = o

Third law of thermodynamics is also known as Nernst heat theorem.

Third law of thermodynamics imposes a limitation on the value of entropy

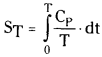
Third law of thermodynamics is useful for calculating the entropy (S) of a substance at any temperature if temperature dependence C_p is known in evaluating the absolute value of entropy.

Basing on the third law of thermodynamics, standard molar entropy of a substance can be calculated at any specified temperature. C_p cannot be measured at absolute zero (-273°C) or around absolute zero. The heat capacity at constant volume (C_v) is measured at various temperatures upto as low temperatures as possible. C_v value at absolute zero is obtained by using extrapolating technique and the Debye equation.
C_v = aT³ (α is constant for a substance)

Near to absolute zero C_p – C_v is negligible. So C_p = C_v. Hence absolute entropy S° can be calculated using C_v value.

Question 41.
Explain “Entropy” concept.
Answer:
Entropy :
Entropy means transformation. It is denoted by ‘S’.

Entropy is a measure of disorder or randomness in a system.

The greater the disorder in a system the higher is the entropy. Entropy is a state function. Entropy change (∆S) between any two states is therefore given by the equation.
∆S = \(\frac{q_{rev}}{T}\)

q_rev is the heat absorbed by the system isothermally and reversibly at T during the state change.

A substance in solid state have lowest entropy because the particles are orderly arranged. The gaseous state of the same substance have highest entropy because the particles are moving most disorderly. The liquid state of the same substance have entropy in between the values for solid and the gaseous state.

For a spontaneous process in an isolated system the change in entropy (∆S) is positive.

Question 42.
Explain spontaneity of a process in terms of Gibbs energy.
Answer:
Gibbs Energy :
Gibbs energy is a thermodynamic function. This is the difference in the enthalpy (H) and the product of entropy and absolute temperature (T) of the system.
G = H – TS
Gibbs energy is the amount of energy available from a system which can be put to useful work at constant temperature and pressure.

The change in Gibbs energy for the system ∆G_system at constant temperature is
∆G_system = ∆H_system – T∆s_system
If ∆G_system is negative (< 0) the process is spontaneous.
If ∆ G_system is positive (> 0) the pro-cess is non-spontaneous.
If ∆ G_system is zero the system has attained equilibrium.

Question 43.
The sign and magnitude of Gibbs energy change of a chemical process tells about its spontaneity and useful work that could be extracted from it. Explain.
Answer:
The process which takes place on its own accord without the aid of an external agency is called spontaneous process. To sum up, the criteria for spontaneity of a process in terms of AG can be given as
i) If ∆G is -ve the prodess is spontaneous
ii) If ∆G is zero, the process does not occur (or) the system is in equilibrium
iii) If ∆G is +ve, the process does not occur in the forward direction The spontaneity of a reaction and the algebraic signs of ∆H, ∆S, ∆G and the magnitude of T are related to each other as given in the below table.

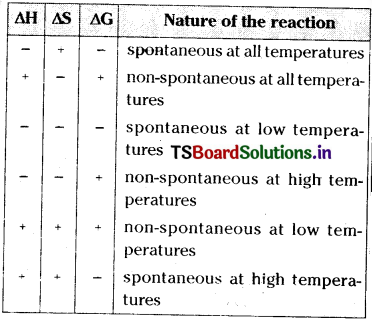
For a spontaneous process in an isolated system the change in entropy should be positive. But many reactions with ∆S is negative are known to occur spontaneously. These reactions takes place on account of coupling of these reactions with reactions of large negative ∆G values.

Question 44.
In a process, 701 J of heat is absorbed by a system and 394 J of work is done by the system. What is the change in internal energy for the process?
Answer:
dq = dU – dW
701 = dU -(- 394 J)
dU = 701 – 394 = 307 J
So the change in internal energy for the process = 307 J.

Question 45.
The reaction of cyan amide (s), with dioxygen, was carried out in a bomb calorimeter and ∆U was found to be – 742.7 kJ mol^-1 at 298 K. Calculate the enthalpy change for the reaction at 298 K.
NH₂CN_(g) + \(\frac{3}{2}\)O₂(g) → N_2(g) + CO_2(g) + H₂O_(l)
Answer:
Number of gaseous molecules of reactants
= 1 + 1.5 = 2.5
Number of gaseous molecules of products
= 1 + 1 +0 = 2
∆n = 2-2.5 = -0.5
∆H = ∆U + ∆nRT
= – 742.7 + (- 0.5 × 8.314 × 10^-3 × 298)
= – 743.9 kJ

Question 46.
Calculate the number of kJ of heat necessary to rise the temperature of 60.0 g of aluminium from 35°C to 55°C. Molar heat capacity of aluminium is 24 J mol^-1 K^-1.
Answer:
q = msdT
q = heat liberated
m = mass of aluminium
s = molar heat capacity of aluminium
dT = change in temperature
q = \(\frac{60}{27}\) × 24 × 20 = 1.09 kJ.

Question 47.
Calculate the enthalpy change on freezing of 1.0 mol of water at 10,0°C to ice at – 10.0°C.
∆_fusH = 6 03 kJ^-1 at 0°C.
Cp[H₂ O(l)] = 75.3 J mol^-1K^-1
C_p[H₂O(s)] = 36.8 J mol^-1K^-1
Answer:

In the first step heat evolved ∆H = nC_pdT = – 75.3 × 10 = – 753 J
In the second step heat evolved ∆H = – 6.0312 J
In the third step heat evolved ∆H = nC_pdT = + 36.8 × 10 = + 368 J
∴ ∆H = – 6.03 + (- 0.753) + (+ 0.368) = – 6.415 kJ

Question 48.
Enthalpy of combustion of carbon to CO₂ at 298 K. Calculate the enthalpy change is – 393.5 kJ mol^-1. Calculate the heat released upon formation of 35.2 g of CO₂
Answer:
Moles of CO₂ = \(\frac{35.2}{44}\) = 0.8
Heat of formation of CO₂ = (- 393.5) (0.8)
= – 315 kJ

Question 49.
Enthalpies of formation of CO(g), CO₂(g), N₂O(g) and N₂O₄(g) are -110, – 393.81 and 9.7 kJ mol^-1 respectively. Find the value of D_rH for the reaction :
N₂O₄(g) + 3CO(g) → N₂O(g) + 3CO₂(g)
Answer:
N₂O₄(g) + 3CO(g) → N₂O(g) + 3CO₂(g)
∆H = (3H_CO2 + H_N2O – (H_N2O4 + 3H_CO)
= [3 × (-389) + 8l]-[9.7 + 3(-110)]
= -778kJ

Question 50.
Given N₂(g) + 3H₂(g) → 2NH₃(g);
∆_rH^θ = – 92.4 kJ mol^-1
What is the standard enthalpy of formation of NH₃ gas?
Answer:
The heat of reaction ∆_rH^θ is – 92.4 kJ mol^-1

This is the heat of formation of 2 moles of ammonia.

The enthalpy of formation of 1 mol of NH₃ = \(\frac{-94.4}{2}\) =-462kJ
∴ Standard enthalpy of formation of ammonia = – 46.2 kJ

Question 51.
Calculate the standard enthalpy of formation of CH₃OH(I) from the following data:

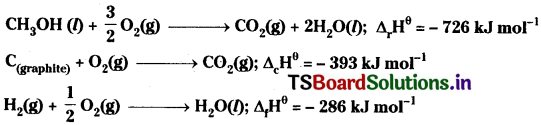
Answer:
The given data

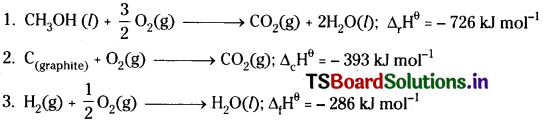
Multiply the equation with 2 and then add the three reactions after reversing the equation,

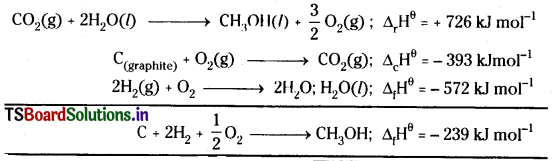
Question 52.
Calculate the enthalpy change for the process
CCl₄(g) → C(g) + 4 Cl(g)
and calculate bond enthalpy of C – Cl in CCl₄(g).
∆_vapH^θ (CCl₄) = 30.5 kJ mol^-1
∆_fH^θ (CCl₄) = – 135.5 kJ mol^-1
∆₀H^θ (C) = 715.0 kJ mol^-1, where
∆_aH^θ is enthalpy of atomisation
∆_aH^θ(Cl₂) = 242 kJ mol^-1.
Answer:

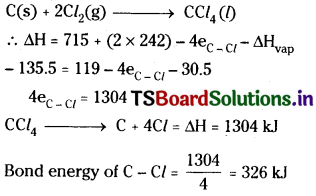
Question 53.
For an isolated system, ∆U = 0 what will be ∆S?
Answer:
Entropy increases (i.e.,) ∆S > 0

Question 54.
For the reaction at 298 K,
2A + B → C
∆H = 400 kJ mol^-1 and ∆S = 0.2 kJ K^-1mol^-1. At what temperature will the reaction become spontaneous considering ∆H and ∆S to be constant over the temperature range?
Answer:
At equilibrium ∆G = 0
T_equl = \(\frac{\Delta \mathrm{H}}{\Delta \mathrm{S}}=\frac{400}{0.2}\) = 2000k
The reaction is spontaneous over 2000 °k.

Question 55.
For the reaction,
2Cl(g) → Cl₂(g), what are the signs of ∆H and ∆S?
Answer:
In the bond formation energy is released.
∴ ∆H = – ve
In this reaction two chlorine atoms combine to form one Cl₂ molecule. Entropy decreases
∴ ∆S = – ve

Question 56.
For the reaction
2A(g) + B(g) → 2D(g)
∆U^θ = -10.5 kJ and ∆S^θ = -44.1 JK^-1.
Calculate ∆G^θ for the reaction, and predict whether the reaction can occur spontaneously or not.
Answer:
∆H = ∆U + ∆n_gRT
∆H = – 10.5 + (- 1) × 8.314 × 10^-3 × 298
= -12.97 kJ

∆G = ∆H – T∆S
= -12.97-298 (-44.1 × 10^-3) = 0.164 kJ

Question 57.
The equilibrium constant for a reaction is 10. What will be the value of ∆G?
R = 8.314 JK^-1mol^-1, T = 300 K.
Answer:
∆G^θ = -2.303 RT log K_p
= – 2.303 × 8.314 × 300 × 1
= – 5.744 kJ mol

Question 58.
State the first law of thermodynamics. Explain its mathematical notation.
Answer:
Energy can neither be created nor be destroyed but energy in a process may be converted from one form to another form. First law of thermodynamics is also known as law of conservation of energy.

Mathematically first law of thermodynamics can be represented as
Q = ∆E + W

where
Q = Amount of heat absorbed by the system
∆E = Increase in internal energy of the system
W = Work done on a system
For infinitesimally small changes
q = dE + W

According to first law of thermodynamics, a part of the amount of heat (Q) absorbed by the system is used for increasing the internal energy (∆E) of the system and the remaining part is used for doing work (w).

Heat absorbed by the system is given + sign, heat given out by the system is given – sign.
Work done by a system is given – sign and work done on a system is given + sign.

Question 59.
State the second law of thermodynamics in any two ways.
Answer:
Second law of thermodynamics may be stated as
Heat cannot flow from a colder body to a hotter body on its own.
(or)

Heat cannot be converted into work completely without causing some permanent changes in the system involved or in the surroundings.
(or)
All spontaneous processes are thermodynamically irreversible and entropy of the system increases in all spontaneous processes.
(or)
It is impossible to construct a machine which is working in cycles that can transform heat from lower temperature to higher temperature without the help of an external agency.

Second law of thermodynamics is useful in predicting

1. Whether a process occurs in a specified direction or not on its own without the intervention of any external agency i.e., whether a process is spontaneous or not in the specified direction.
2. If a transformation or a process occurs, what fraction of one form of energy is converted into another form of energy in this transformation or process.
3. A machine which transfers heat from lower temperature to higher temperature on its own is called perpetual motion machine of second
   kind. Second law of thermodynamics predicts that perpetual motion machine is not possible.

Question 60.
Explain Gibbs energy.
Answer:
Gibbs Energy :
Gibbs energy is a thermodynamic function. This is the difference in the enthalpy (H) and the product of entropy and absolute temperature (T) of the system.
G = H – TS
Gibbs energy is the amount of energy available from a system which can be put to useful work at constant temperature and pressure.

The change in Gibbs energy for the system ∆G_system at constant temperature is
∆G_system = ∆H_system – T∆s_system
If ∆G_system is negative (< 0) the process is spontaneous.
If ∆ G_system is positive (> 0) the pro-cess is non-spontaneous.
If ∆ G_system is zero the system has attained equilibrium.

Question 61.
Explain the spontaneity of a reaction in terms of Gibbs energy.
Answer:
The process which takes place on its own accord without the aid of an external agency is called spontaneous process. To sum up, the criteria for spontaneity of a process in terms of AG can be given as
i) If ∆G is -ve the prodess is spontaneous
ii) If ∆G is zero, the process does not occur (or) the system is in equilibrium
iii) If ∆G is +ve, the process does not occur in the forward direction The spontaneity of a reaction and the algebraic signs of ∆H, ∆S, ∆G and the magnitude of T are related to each other as given in the below table.

For a spontaneous process in an isolated system the change in entropy should be positive. But many reactions with ∆S is negative are known to occur spontaneously. These reactions takes place on account of coupling of these reactions with reactions of large negative ∆G values.

Long Answer Questions

Question 1.
State and explain Hess’s law of constant heat summation. Give example. [AP ’17]
Answer:
Hess’s law :
Energy changes remains constant whether the reactions takes place in single step or in several steps. [TS Mar. ’19]

I. Formation of CO₂ : CO₂ can be formed either in one step or in two steps.
a) C_(graphite) + O₂ (g) → CO₂ (g), ∆H = – 393.5 kJ
b) C_(graphite) + \(\frac{1}{2}\)O₂ (g) → CO (g), ∆H = -110.5 kJ
CO (g) + \(\frac{1}{2}\)O₂(g) → CO₂(g),
∆H = – 283.5 kJ ,
Total ∆H = – 393.52 kJ

Reaction ‘a’ is completed in single step and reaction ‘b’ is completed in two steps. But in both the cases energy changes remain constant, which proves Hess’s law.

II. Formation of NH₄Cl (aq) :
a) NH₃ (g) + H₂O (l) → NH₃ (aq), ∆H = – 35.1 kJ
HCl (g) + H₂O (l) → HCl (aq), ∆H = – 72.9 kJ
NH₃ (aq) + HCl (aq) → NH₄Cl (aq), ∆H = -51.5 kJ
Total ∆H = – 159.5 kJ

b) NH₃(g) + HCl (g) → NH₄Cl (g), ∆H = -176.1 kJ
NH₄Cl (S) + H₂O (l) → NH₄Cl (aq), ∆H = + 16.3 kJ .
Total ∆H = – 159.8 kJ

In both reactions (a) and (b), the heat of formation of NH₄Cl (aq.) is the same, which proves Hess’s law.

Uses of Hess’s law: It is used to determine

1. Heat of formation.
2. Heat of reaction.
3. Crystal lattice energy.
4. Transition temperatures of allotropic forms.

Question 2.
Explain the experiment to determine the internal energy change of a chemical reaction.
Answer:
The change in internal energy ∆U in a chemical reaction can be determined using bomb calorimeter. The bomb is a steel vessel. It is immersed in a water bath. The whole device is called calorimeter.
Bomb Calorimeter

A combustible substance is burnt in pure oxygen supplied in the steel bomb. The heat evolved during the reaction measured from the rise in the temperature. Since the bomb calorimeter is sealed, the energy changes taking place in it are considered as that taking place at constant volume. Temperature change of the calorimeter produced by the reaction is then converted to qv by using the known heat capacity of the calorimeter.
q = – C × \(\frac{M}{W}\) × ∆T
where C’ is the heat capacity of calorimeter
∆T is the change in temperature
W is the mass of substance
M is the molecular mass of substance taken.

Question 3.
Explain the experiment to determine the enthalpy change of a chemical reaction.
Answer:
The change of enthalpy ∆H of a reaction can be measured in a calorimeter as shown in the figure. However the calorimeter is kept open to the atmosphere.
Calorimeter for measuring heat changes at constant pressure (atmospheric pressure)

The calorimeter is immersed in an insulated water bath fitted with stirrer and thermometer. The temperature of the bath is recorded in the beginning and after the end of the reaction and change in temperature is recorded. Knowing the heat capacity of water bath and calorimeter and also the change in temperature, the heat absorbed or evolved in the reaction can be calculated. This gives the enthalpy change (∆H) of the reaction.

Question 4.
Explain the spontaneity of a reaction in terms of enthalpy change, entropy change and Gibbs energy change.
Answer:
The process which takes place on its own accord without the aid of an external agency is called spontaneous process. To sum up, the criteria for spontaneity of a process in terms of AG can be given as
i) If ∆G is -ve the prodess is spontaneous
ii) If ∆G is zero, the process does not occur (or) the system is in equilibrium
iii) If ∆G is +ve, the process does not occur in the forward direction The spontaneity of a reaction and the algebraic signs of ∆H, ∆S, ∆G and the magnitude of T are related to each other as given in the below table.

For a spontaneous process in an isolated system the change in entropy should be positive. But many reactions with ∆S is negative are known to occur spontaneously. These reactions takes place on account of coupling of these reactions with reactions of large negative ∆G values.

Additional Questions & Answers

Question 1.
Express the change in internal energy of a system when
i) No heat is absorbed by the system from the surroundings, but work (w) is done on the system. What type of wall does the system have?
ii) No work is done on the system, but q amount of heat is taken out from the system and given to the surroundings. What type of wall does the system have?
iii) w amount of work is done by the system and q amount of heat is supplied to the system. What type of system would it be?
Answer:
i) ∆U = w_ad’ wall is adiabatic

ii) ∆U = – q, thermally conducting walls

iii) ∆U = q – w, closed system.

Question 2.
Two litres of an ideal gas at a pressure of 10 atm expands isothermally into a vacuum until its total volume is 10 litres. How much heat is absorbed and how much work is done in the expansion?
Answer:
We have q = -w = p_ex (10 – 2) = 0(8) = 0 No work is done; no heat is absorbed.

Question 3.
Consider the same expansion, but this time against a constant external pressure of 1 atm.
Answer:
We have q = – w = p_ex (8) = 8 iitre-atm

Question 4.
Consider the same expansion, to a final volume of 10 litres conducted reversibly.
Answer:
We have q = – w = 2.303 × 20 log \(\frac{10}{2}\) = 32.2 litre-atm.