TS 6th Class Maths Solutions Chapter 9 Introduction to Algebra InText Questions

Students can practice TS SCERT Class 6 Maths Solutions Chapter 9 Introduction to Algebra InText Questions to get the best methods of solving problems.

TS 6th Class Maths Solutions Chapter 9 Introduction to Algebra InText Questions

Try These

Question 1.
Can you now write the rule to form the following pattern with match-sticks ?

Answer:
The rule for the above figures is 3n.
[∵ 3 × 1, 3 × 2, 3 × 3, ………………]

Question 2.
Find the rule for required number of matchsticks to form a pattern repeating ‘H’. How would the rule be for repeating the shape ‘L’ ?
Answer:
The required pattern of repeating ‘H’ is
‘3n’. (3 × 1, 3 × 2, ………………..)
The rule for ‘L’ is ‘2n’.

Question 3.
A line of shapes is constructed using matchsticks.

(i) Find the rule that shows how many sticks are needed to make a group of such shapes ?
(ii) How many matchsticks are needed to form a group of 12 shapes ?
Answer:
(i) Number of matchsticks that are used in each figure are
3 ; 5 ; 7 ; 9 ………………
Shape-1; Shape-2; Shape-3; Shape-4
2 × 1 + 1; 2 × 2 + 1 ; 2 × 3 + 1 ; 2 × 4 + 1 ………
In general (2n + 1) is the rule for the above shapes.

(ii) 2n + 1 = 2 × 12 + 1 = 25 [ ∵ n = 12]

(Try These)

Question 1.
Find the general rule for the perimeter of a rectangle. Use variables ‘l’ and ‘b’ for length and breadth of the rectangle respectively.
Answer:

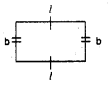
Perimeter of a rectangle
= l + b + l + b
= 2l + 2b = 2 (l + b)

Question 2.
Find the general rule for the area of a square by using the variable ’s’ for the side of a square ?
Answer:

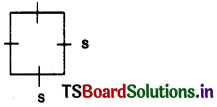
The rule for the area of a square is A = side × side
= s × s
A = s²

Question 3.
What would be the rule for perimeter of an Isosceles triangle ?
Answer:

The rule for the perimeter of an Isosceles triangle
= 3 × side
= 3 × a
P = 3a

Do This

Question 1.
Find the n^th term in the following sequences.
(i) 3, 6, 9, 12, …………………
(ii) 2, 5, 8, 11, …………………
(iii) 1, 8, 27, 64, 125, …………………
Answer:
(i) The n^th> term of the above series is
3 × 1, 3 × 2, 3 × 3, ……………….. = 3n.

(ii) The n^th term is 3 × 1 – 1, 3 × 2 – 1, 3 × 3 – 1, 3 × 4 – 1,
i.e., 3n – 1

(iii) The nth term is 1 × 1 × 1, 2 × 2 × 2, 3 × 3 × 3, ……. is
1³, 2³, 3³ ………………….
i.e., n³

Question 2.
Write LHS and RHS of the following simple equations:
(i) 2x + 1 = 10
Answer:
2x + 1 = 10
LHS = 2x + 1, RHS = 10

(ii) 9 = y – 2
Answer:
9 = y – 2 ;
LHS = 9, RHS = y – 2

(iii) 3p + 5 = 2p + 10
Answer:
3p + 5 = 2p + 10
LHS = 3p + 5, RHS = 2p + 10

Question 3.
Write any two simple equations and give their LHS and RHS.
Answer:

Simple equation	LHS	RHS
1. 4x – 10 = 7x + 6	4x – 10	7x + 6
2. t – 2= 5	t – 2	5

Question 4.
Find the solution of the equation ‘x – 4 = 2’ by Trail and Error method.
Answer:
Given equation is x – 4 = 2
If x = 1 ⇒ x – 4 = 2
⇒ 1 – 4 = 2
– 3 ≠ 2
If x = 3 ⇒ 3 – 4 = 2
– 1 ≠ 2
If x = 5 ⇒ 5 – 4 = 2 .
1 ≠ 2
If x = 6 ⇒ 6 – 4 = 2
2 = 2
x = 6 satisfies the given equation.
∴ x = 6 is the solution of the equation.