TS 10th Class Maths Solutions Chapter 3 Polynomials Ex 3.2

Students can practice TS 10th Class Maths Solutions Chapter 3 Polynomials Ex 3.2 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 3 Polynomials Exercise 3.2

Question 1.
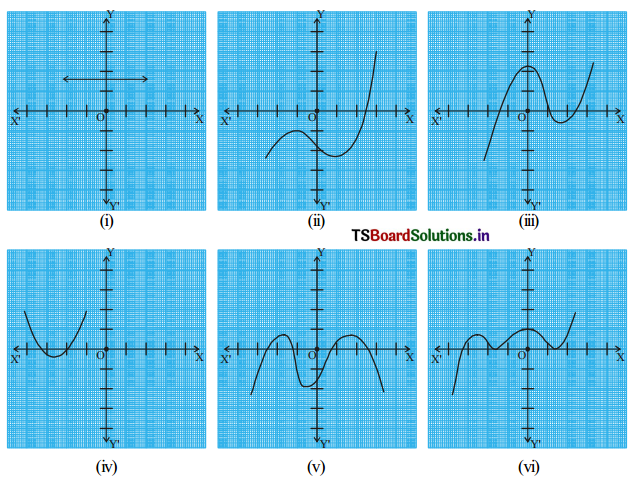
The graphs of y = p(x) are given in the figure below, for some polynomials p(x). In each case, find the number of zeroes
of p(x).
Solution:

Solution:
Six figures are given and they are numbered.
In the first figure, there are no zeroes.
In the second figure, there is one zero.
In the third figure, there are three zeroes.
In the fourth figure, there are two zeroes.
In the fifth figure, there are four zeroes.
In the sixth figure, there are three zeroes.

Question 2.
Find the zeroes of the given polynomials.
(i) p(x) = 3x
(ii) p(x) = x² + 5x + 6
(iii) p(x) = (x + 2) (x + 3)
(iv) p(x) = x⁴ – 16
Solution:
i) p(x) = 3x
p(0) = 3 × 0 = 0
∴ The zero of p(x) = 3x is 0

ii) p(x) = x² + 5x + 6
= x² + 3x + 2x + 6
= x(x + 3) + 2(x + 3) = (x + 2) (x + 3)
To find zeroes, let p(x) = 0
⇒ (x + 2) (x + 3) = 0
So, x + 2 = 0 (or) x + 3 = 0
⇒ x = -2 (or) x = -3
Therefore, the zeroes of x + 5x + 6 are – 2 and -3.

iii) p(x) = (x + 2) (x + 3)
⇒ x² + 2x + 3x + 6
⇒ x² + 5x + 6
To find zeroes, let p(x) = 0
⇒ (x + 2) (x + 3) = 0
So, x + 2 = 0 (or) x + 3 = 0
⇒ x = -2 (or) x = -3
∴ The zeroes of (x + 2) (x + 3) are -2 and -3.

iv) p(x) = x⁴ – 16
= (x²)² – (4)² = (x² + 4) (x² – 4)
= (x² + 4)(x + 2)(x – 2)
To find zeroes, let p(x) = O
⇒ (x² + 4) (x + 2)(x – 2) = 0
(i.e.,) x² + 4 = 0 (or) x + 2 = 0 (or) x – 2 = 0
If x² + 4 = 0, then x² = -4 ⇒
x = ± \(\sqrt{-4}\)
If x + 2 = 0, then x = -2
If x – 2 = 0, then x = 2
∴ The zeroes of the polynomial x⁴ – 16 are -2, 2 and ± \(\sqrt{-4}\).

Question 3.
Draw the graphs of the given polynomials and find the zeroes. Justify the answers. (A.P.June’ 15)
(i) p(x) = x² – x – 12
(ii) p(x) = x² – 6x + 9
(iii) p(x) = x² – 4x + 5
(iv) p(x) = x² + 3x – 4
(v) p(x) = x² – 1
Solution:
i) p(x) = x² – x – 12

∴ The zeros of x² – x – 12 are 4 and -3.

Scale:
On X-axis: 1 cm = 1 unit
OnY-axis: 1 cm = 2 units

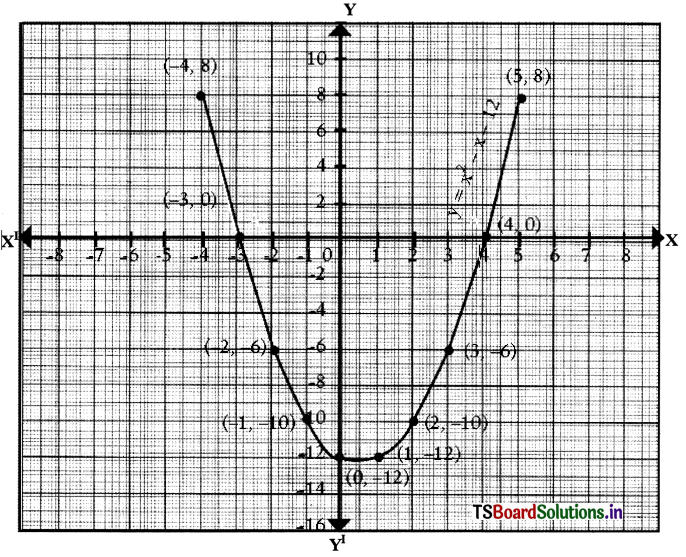
The graph intersects the X-axis at (4, 0) and (-3, 0)

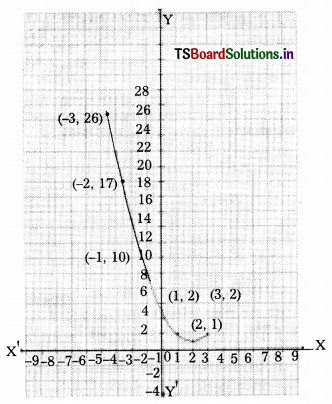
ii) p(x) = x² – 6x + 9


The graph intersects one the X-axis at only point (3, 0)

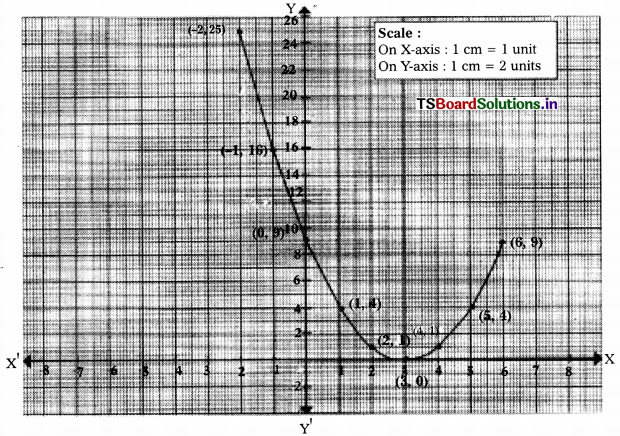
iii) p(x) = x² – 4x + 5

Scale:
On X-axis: 1 cm = 1 unit
OnY-axis: 1 cm = 2 units

The graph does not intersect at the X-axis.
There are no zeroes of the polynomial x² – 4x + 5

iv) p(x) = x² + 3x – 4


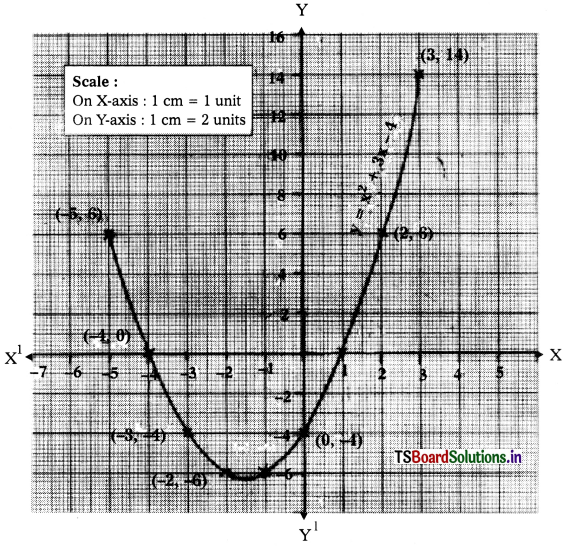
∴ The graph intersects the X-axis at (1, 0) and (-4, 0)
∴ The zeroes of the polynomial x² + 3x – 4 are 1 and -4.

v) p(x) = x² – 1


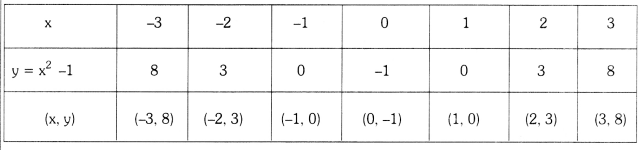
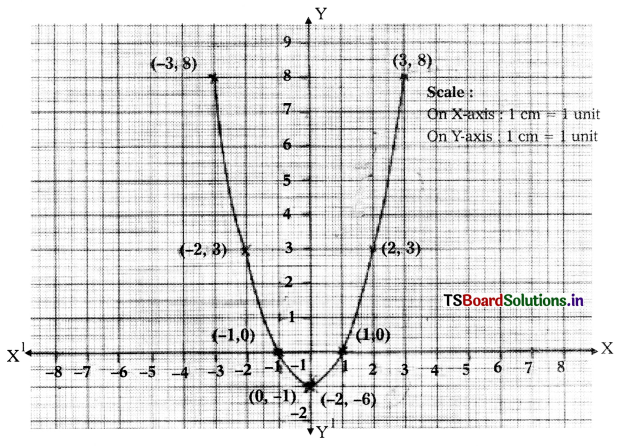
The graph intersects the X-axis at (-1, 0) and (1, 0)
∴ The zeroes of the polynomial x² – 1 are -1 and 1.

Question 4.
Why are \(\frac{1}{4}\) and -1 zeroes of the polynomial p(x) = 4x² + 3x – 1?
Solution:
p(x) = 4x² + 3x – 1
∴ p(\(\frac{1}{4}\)) = 4(\(\frac{1}{4}\))² + 3(\(\frac{1}{4}\)) – 1
= \(\frac{1}{4}\) + \(\frac{3}{4}\) + \(\frac{1}{1}\)
= \(\frac{1+3-4}{4}\) = \(\frac{0}{4}\) = 0
∴ p(-1) = 4(-1)² + 3(-1) – 1
= 4(1) – 3 – 1
= 4 – 3 – 1
= 4 – 4 = 0
Since p(\(\frac{1}{4}\)) and p(-1) are equal to zero.
\(\frac{1}{4}\) and -1 are the zeroes of the polynomial.