TS 10th Class Maths Solutions Chapter 3 Polynomials Ex 3.3

Students can practice TS 10th Class Maths Solutions Chapter 3 Polynomials Ex 3.3 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 3 Polynomials Exercise 3.3

Question 1.
Find the zeroes of the following quadratic polynomial and verify the relationship between the zeroes and coefficients.

i) x² – 2x – 8
ii) 4s² – 4s + 1
iii) 6x² – 3 – 7x
iv) 4u² + 8u
v) t² – 15
vi) 3x² – x – 4
Solution:
i) Let p(x) = x² – 2x – 8
= x² – 4x + 2x – 8
= x(x – 4) + 2(x – 4)
= (x + 2) (x – 4)
The zeroes of p(x) are given by P(x) = 0
⇒ (x + 2) (x – 4) = 0
⇒ x + 2 = 0 (or) x – 4 = 0
⇒ x = -2 (or) x = 4
Hence the zeroes of x² – 2x – 8 are -2 and 4.
Sum of the zeroes = -2 + 4 = 2

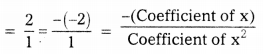
Product of the zeroes = -2 × 4 = -8

ii) Let p(s) = 4s² – 4s + 1
= (2s)² – 2(2s) (1) + (1)²
= (2s – 1)²
= (2s – 1) (2s – 1)
The zeroes of p(s) are given by p(s) = 0
⇒ (2s – 1) (2s – 1) = 0
⇒ 2s – 1 =0 (or) 2s – 1 = 0
⇒ s’ = \(\frac{1}{2}\) (or) s = \(\frac{1}{2}\)
Hence the zeroes of 4s² – 4s + 1 are \(\frac{1}{2}\), \(\frac{1}{2}\)
Sum of the zeroes = \(\frac{1}{2}\) + \(\frac{1}{2}\) = 1;

(iii) Let p(x) = 6x² – 7x – 3
= 6x² – 9x + 2x – 3
= 3x(2x – 3) + 1 (2x – 3)
= (3x + 1) (2x – 3)
The zeroes of p(x) are given by p(x) = 0
⇒ (3x + 1) (2x – 3) = 0
⇒ 3x + 1 = 0 (or) 2x – 3 = 0
⇒ 3x = -1 (or) 2x = 3
⇒ x = \(\frac{-1}{3}\) (or) x = \(\frac{3}{2}\)
Hence the zeroes of 6x – 7x – 3 are \(\frac{-1}{3}\) and \(\frac{3}{2}\)
Sum of the zeroes = \(\frac{-1}{3}\) + \(\frac{3}{2}\)

iv) Let p(u) = 4u² + 8u
= 4u(u + 2)
The zeroes of p(u) are given by
⇒ p(u) = 0
⇒ 4u(u + 2) = 0
⇒ 4u = 0 (or) u + 2 = 0
⇒ u = 0 (or) u = -2
Hence the zeroes of 4u + 8u are 0 and -2.
Sum of the zeroes = 0 + (-2) = -2

v) Let p(t) = t² – 15
The zero of p(t) is given by p(t) = 0
⇒ t² – 15 = 0 ⇒ t² = 15

vi) Let P(x) = 3x²
The zero of p(x) is given by P(x) = 0
⇒ 3x² – x – 4 = 0
⇒ 3x² + 3x – 4x – 4 = 0
⇒ 3x(x + 1) – 4(x + 1) = 0
⇒ (x + 1) (3x – 4) = 0
⇒ x + 1 = 0 (or) 3x – 4 = 0
⇒ x = -1 (or) x = 4/3
Hence the zeroes of 3x² – x – 4 are -1 (or) 4/3
Sum of the zeroes of 3x² – x – 4 are -1 (or) 4/3.
Sum of the zeroes =

Question 2.
Find the quadratic polynomial in each case, with the given numbers as the sum and product of its zeroes respectively.

i) \(\frac{1}{4}\), -1
ii) \(\sqrt{2}\), \(\frac{1}{3}\)
iii) 0, \(\sqrt{5}\)
iv) 1, 1
v) –\(\frac{1}{4}\), \(\frac{1}{4}\)
vi) 4, 1 (A.P. Mar. ’15)
Solution:
i) \(\frac{1}{4}\), -1
Let α, β be the zeroes of the quadratic polynomial.
Sum of the zeroes = α + β = \(\frac{1}{4}\)
Product of the zeroes = αβ = -1
The required quadratic polynomial will be
k[x² – x (α + β) + αβ] where k is a constant
⇒ k[x² – x(\(\frac{1}{4}\)) + (-1)]
⇒ k(x² – \(\frac{x}{4}\) – 1)
If k = 4, then the polynomial will be 4(x² – \(\frac{x}{4}\) – 1) = 4x² – x – 4

ii) \(\sqrt{2}\), \(\frac{1}{3}\)
Let α, β be the zeroes of the quadratic polynomial.
Sum of the zeroes = α + β = \(\sqrt{2}\)
Product of the zeroes = αβ = \(\frac{1}{3}\)
∴ The required quadratic polynomial will be
k[x² – x(α + β) + αβ] where k is a constant
⇒ k[x² – x(\(\sqrt{2}\)) + \(\frac{1}{3}\)]
⇒ k[x² – \(\sqrt{2}\)x + \(\frac{1}{3}\)]
when k = 3, then the polynomial will be
3[x² – \(\sqrt{2}\)x + \(\frac{1}{3}\)] (or) 3x² – 3\(\sqrt{2}\)x + 1

iii) 0, \(\sqrt{5}\)
Let α, β be the zeroes of the quadratic polynomial.
Sum of the zeroes = α + β = 0
Product of the zeroes = αβ = \(\sqrt{5}\)
The required quadratic polynomial will be k[x² – x(α + β) + αβ where k is a constant
⇒ k[x² -x(0) + \(\sqrt{5}\)]
⇒ k[x² + \(\sqrt{5}\)].
Where k = 1, the polynomial will be x² + \(\sqrt{5}\).

iv) 1, 1
Let α, β be the zeroes of the quadratic polynomial.
Sum of the zeroes = α + β = 1
Product of the zeroes = αβ = 1
∴ The required quadratic polynomial will be
k[x² – x(α + β) + αβ] where k is a constant
⇒ k[x² – x(α – β) + 1]
⇒ k[x² – x + 1]
Where k = 1, the polynomial will be x² – x + 1.

v) –\(\frac{1}{4}\), \(\frac{1}{4}\)
Let α, β be the zeroes of the quadratic polynomial.
Sum of the zeroes = α + β = –\(\frac{1}{4}\)
Product of the zeroes = αβ = \(\frac{1}{4}\)
The required quadratic polynomial will be k[x² – x(α + β) + αβ] where k is a constant
⇒ k[x² – x(-\(\frac{1}{4}\)) + \(\frac{1}{4}\)]
⇒ k[x² + \(\frac{x}{4}\) + \(\frac{1}{4}\)]
Where k = 4, the polynomial will be
4[x² + \(\frac{x}{4}\) + \(\frac{1}{4}\)] = 4x² + x + 1

Question 3.
Find the quadratic polynomial for the zeroes α, β given in each case. (A.P.Mar.’16)

i) 2, -1
ii) \(\sqrt{3}\), –\(\sqrt{3}\)
iii) \(\frac{1}{4}\), -1
iv) \(\frac{1}{2}\), \(\frac{3}{2}\)
Solution:
i) 2,-1
Let the quadratic polynomial be ax² + bx + c, a ≠ 0 and its zeroes be α & β
Here α = 2, β = -1
Sum of the zeroes = α + β = 2 + (-1) = 1
Product of the zeros = αβ = 2 × (-1)
= -2
∴ The required quadratic polynomial
ax² + bx + c is k[x² – x(α + β) + αβ]
where k is a constant
⇒ k [x² – x(1) + (-2)]
⇒ k[x² – x – 2]
Where k = 1, the quadratic polynomial will be x² – x – 2.

ii) \(\sqrt{3}\), –\(\sqrt{3}\)
Let the quadratic polynomial be
ax² + bx + c, a ≠ 0 and its zeroes be α & β
Here α = \(\sqrt{3}\) , β = –\(\sqrt{3}\)
Sum of the zeroes = α + β
= \(\sqrt{3}\) + (-\(\sqrt{3}\)) = o
Product of the zeros
= αβ = \(\sqrt{3}\) × –\(\sqrt{3}\) = -3
Therefore the quadratic polynomial
ax² + bx + c is k[x² – x(α + β) + αβ]
where k is a constant
⇒ k [x² – x(0) + (-3)]
⇒ k[x² – 3]
Where k = 1, the quadratic polynomial will be [x² – 3].

iii) \(\frac{1}{4}\), -1
Let the quadratic polynomial be
ax² + bx + c, a ≠ 0 and its zeroes be α & β
Here α = \(\frac{1}{4}\), β = -1
Sum of the zeroes = α + β
= \(\frac{1}{4}\) + (-1) = \(\frac{-3}{4}\)
Product of the zeroes = αβ = \(\frac{1}{4}\) × (-1)
= –\(\frac{1}{4}\)
Therefore, the quadratic polynomial
ax² + bx + c is k[x² – x(α + β) + αβ]
where k is a constant
Where k = 4, the quadratic polynomial will be [4x² + 3x – 1]

iv) \(\frac{1}{2}\), \(\frac{3}{2}\)
Let the quadratic polynomial be
ax² + bx + c, a ≠ 0 and its zeroes be α & β
Here α = \(\frac{1}{2}\), β = \(\frac{3}{2}\)
Sum of the zeroes = α + β
= \(\frac{1}{2}\) + \(\frac{3}{2}\) = \(\frac{4}{2}\) = 2
Product of the zeroes = αβ
= \(\frac{1}{2}\) × \(\frac{3}{2}\) = \(\frac{3}{4}\)
Therefore the quadratic polynomial
ax² + bx + c is k[x² – x(α + β) + αβ]
where k is a constant

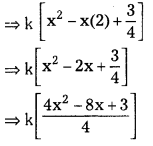
Where k = 4, the quadratic polynomial will be [4x² – 8x + 3].

Question 4.
Verify that 1, -1 and -3 are the zeroes of the cubic polynomial x³ + 3x² – x – 3 and check the relationship between zeroes and the coefficients. (A.P. Mar. ’15)
Solution:
The given polynomial is x³ + 3x² – x – 3
Comparing the given polynomial with ax³ + bx² + cx + d
We get a = 1, b = 3, c = -1, d = -3
Let p(x) = x³ + 3x² – x – 3
Then p(1) = (1)³ + 3(1)² – 1 – 3
= 1 + 3 – 1 – 3
= 4 – 4 = 0
p(-1) = (-1)³ + 3(-1)² – (-1) – 3
= -1 + 3 + 1 – 3 = 0
p(-3) = (-3)³ + 3(-3)² – (-3) – 3
= -27 + 27 + 3 – 3 = 0
Therefore 1, -1 and -3 are the zeroes of
x³ + 3x² – x – 3.
So α = 1, β = -1, γ = -3
α + β + γ = 1 – 1 – 3 = -3 = -3/1 = \(\frac{-b}{a}\)
αβ + βγ + αγ = 1(-1) + (-1)(-3) + (-3)(1)
= -1 + 3 – 3 = -1 = -1/1 = c/a
αβγ = (1)(-1)(-3) = – \(\left(\frac{-3}{1}\right)\) = \(\frac{-\mathrm{d}}{\mathrm{a}}\)