Class 6

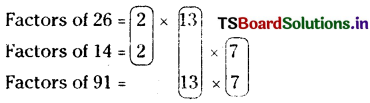
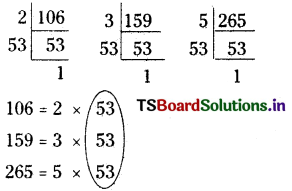
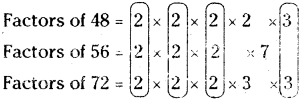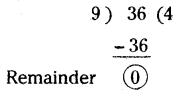Students can practice Telangana 6th Class Maths Textbook Solutions Chapter 6 Integers InText Questions to get the best methods of solving problems.

TS 6th Class Maths Solutions Chapter 6 Integers InText Questions

Do This

Question 1.
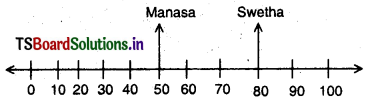
Manasa has borrowed ₹ 50 and Swetha has borrowed ₹ 20 from their mother. How will you represent this on the number line ₹ Suppose their father gave them ₹ 100 each as pocket money, who will have more money after clearing the debit ?
Answer:

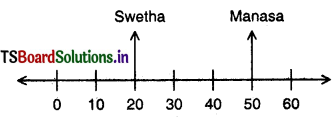
If each of them get ₹ 100 from their father
then amount at Manasa = 100 – 50 = ₹ 50
then amount at Swetha = 100 – 20 = ₹ 80
∴ Amount of Swetha is greater than that of Manasa.

Try These

Question 1.
Collect information about temperatures recorded in various places in India in the month of January and write them using integers.
Answer:
The temperatures of various places in the month of January
1. Hyderabad → 10°C
2. Siachain (J & K) → 20°C
3. Lambasingi → 5°C

Do this

Question 1.
Draw a vertical line and represent the following integers on the number line. – 5, 4, – 7, – 8, – 2, 9, 5, – 6, 2
Answer:
Vertical line :

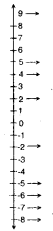
On a number line :

Do This

Question 1.
Fill in the boxes using < or > signs.
(i) 0 ………. -1
Answer:
0 > -1

(ii) -3 ……. – 2
Answer:
-3 < -2

(iii) 5 ……… 6
Answer:
5 < 6

(iv) -4 ……… 0
Answer:
-4 < 0

Do This

Question 1.
Rajesh has a shop CM thp ground floor of a building. There are stairs going up to the terrace and stairs going down to the godown, where goods are stored.
Everyday his daughter Hasini, after coming back from school goes up to the terrace to play. She helps father in arranging things in the godown at night.
Observe the picture and try to answer the questions using integers marked on the steps.

(i) Go 7 steps up from the shop.
(ii) Go 3 steps down from the ground floor.
(iii) Go 5 steps up from the ground floor and then go 3 steps further up from there.
(iv) Go 4 steps down from the ground floor and then further 3 steps from there.
(v) Go down 5 steps down from the ground floor and 10 steps up fmin there.
(vi) Go 8 steps up from the ground floor and come down 9 steps down from there.
Answer:
(i) +7
(ii) -3
(iii) 5 + 3 = + 8
(iv) (-4) + (-3) = -7
(v) (-5) + 10 = +5
(vi) (8) + (-9) = (—1)

Do This

Question 1.
Find the values of the following.
(i) -7 + 8
(ii) -3 + 5
(iii) – 3 – 2
(iv) + 7 – 10
Answer:
(i) (- 7) + (8)
= (- 7) + (+ 7) + (+1)
= [(-7) + (+7)] + (+1)
= 0 + 1 = 1

(ii) (- 3) + (+ 5)
= [(-3) + (+3)] + (+2)
= 0 + 2 = 2

(iii) (-3) +(-2)
= [-(3 + 2)] = -5

(iv) (+7) + (-10)
= (+7) + [(-7) + (-3)]
= [(+7) + (-7)] + (-3)
= 0 – 3
= – 3

Try These

Question 1.
Find the value of the following using a number line.
(i) (- 3) + 5
(ii) (- 5) + 3
Make your own two new questions and solve them using the number line.
Answer:
(i) (- 3) + 5 = (- 3) + (3 + 2) = [- 3 + 3] + 2 = 0 + 2 = 2

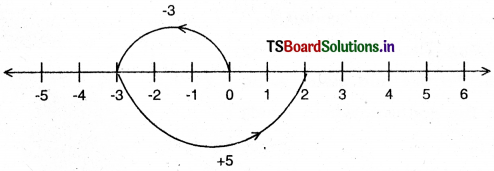
(ii) (- 5) + 3 = [(- 3) + (- 2)] + 3 = [(- 3) + 3] + (- 2) = 0 + (- 2) = – 2

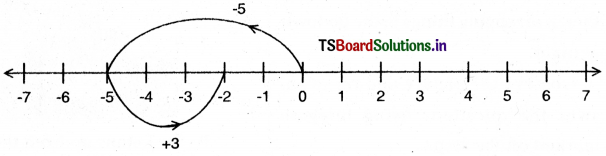
Ex: (i) (-4) + 1 = -3

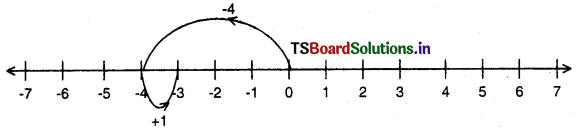
(ii) 6 + (-4) = 2

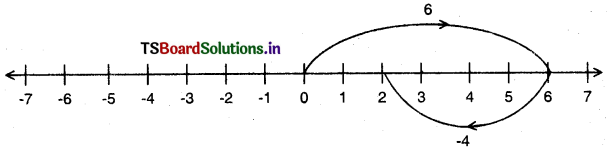
Question 2.
Find the solution of the following:
(i) (+5) + (-5)
(ii) (+6) + (-7)
(iii) (-8) + (+2)
Ask your Mend to give five such questions and solve them.
Answer:
(i) (+ 5) + (- 5) = 5 – 5 = 0
(ii) (+ 6) + (- 7) = (+6) + [(- 6) + (- 1)] = [(+ 6) + (-6)] + (- 1) = 0 + (- 1) = – 1
(iii) – 8 + (+ 2) = [(- 6) + (- 2)] + (+ 2) = (- 6) + [(- 2) + (+ 2)] = (- 6) + 0 = – 6
Five related problems.
(i) (-6) + (-3)
(ii) (+8) + (-5)
(iii) (-16) + 15
(iv) 10 + (-6)
(v) (+11) + (-12)
Answer:
(i) (- 6) + (- 3)
= (- 6) + (- 3)
= – 9

(ii) (+ 8) + (- 5) = [(+ 3) + (+ 5)] + (-5)
= (+ 3) + [(+ 5) + (- 5)]
= (+ 3) + 0 = 3

(iii) (- 16) + 15
= [(- 15) + (- 1)] + 15
= (- 15) + (+ 15) + (- 1)
= – 1

(iv) 10 + (- 6)
= [(+ 4) + (+ 6)] + (- 6)
= (+4) + [(+ 6) + (- 6)]
= (+ 4) + 0 = + 4

(v) (+ 11) + (- 12)
= (+ 11) + [(- 11) + (- 1)]
= [(+ 11) + (- 11)] + (- 1)
= 0 + (- 1)
= – 1

Do This

Question 1.
Find the solution of the following.
(a) -5- (-3)
(b) – 7 – (+2)
(c) – 7 – (-5)
(d) 3 – (-4)
(e) 5 – (+7)
(f) 4 – (- 2)
Sol.
(a) – 5 – (- 3) = – 5 + 3 = – 2
(b) – 7 – (+2) = – 7 – 2 = – 9
(c) – 7 – (- 5) = – 7 + 5 = – 2
(d) 3 – (- 4) = 3 + 4 = + 7
(e) 5 – (+ 7) = 5 – 7 = – 2
(f) 4 – (- 2) = 4 + 2 = + 6

Think, Discuss And Write

Question 1.
Observe that as the number we subtract from 3 is decreasing, the result obtained is increasing. Is it true for all integer’s?
3 – 3 = 0
3 – 2 = 1
3 – 1 = 2
3 – 0 = 3
3 – (-1) = 4
3 – (- 2) = 5
3 – (- 3) = 6
Answer:
No, it is not true for all the integers.
Since 3 – 4 = – 1
3 – 5 = – 2
3 – 6 = – 3 it is decreasing.

Students can practice TS 6th Class Maths Solutions Chapter 3 Playing with Numbers Ex 3.5 to get the best methods of solving problems.

TS 6th Class Maths Solutions Chapter 3 Playing with Numbers Exercise 3.5

Question 1.
Find the LCM of the following numbers by prime factorisation method.
(i) 12 and 15
Answer:
The given numbers are 12 and 15.
Let us e×press each number as a product of prime factors.

The common factor of both = 3
Take the extra factors of both 12 and 15, (i.e.,) 2, 2 and 5
∴ LCM = 2 × 2 × 5 × 3 = 60

(ii) 15 and 25
Answer:
The given numbers are 15 and 25.
Let us express each number as the product of prime factors.

The common factor of both = 5
The extra factors of both = 3 and 5
∴ LCM = 3 × 5 × 5 = 75.

(iii) 14 and 21
Answer:
The given numbers are 14 and 21.
Let us express each number as the product of prime factors.

The common factor of both = 7
The extra factors of both = 2 and 3
∴ LCM = 2 × 3 × 7 = 42

(iv) 18 and 27
Answer:
The given numbers are 18 and 27
Let us express each number as the product of prime factors.

The common factor of both = 3 × 3
The extra factors of both = 2 and 3
∴ LCM = 3 × 3 × 2 × 3 = 54

(v) 48, 56 and 72
Answer:
The given numbers are 48, 56 and 72.
Let us express each number as the product of prime factors.

The common factor of the three numbers = 2 × 2 × 2 × 3
The extra factors of the three numbers = 2 × 3 × 7
∴ LCM = 2 × 2 × 2 × 3 × 2 × 3 × 7 = 1008

(vi) 26, 14 and 91
Answer:
The given numbers are 26, 14 and 91
Let us express each number as the product of prime factors

The common factors of the three numbers = 2 × 13 × 7
There are no extra factors of all the numbers.
∴ LCM = 2 × 13 × 7 = 182

Question 2.
Find the LCM of the following numbers by division method,
(i) 84, 112, 196
Answer:
The given numbers are 84, 112 and 196.

∴ LCM = 2 × 2 × 7 × 3 × 4 × 7 = 2352

(ii) 102, 119, 153
Answer:
The given numbers are 102, 119 and 153.

∴ LCM = 17 × 3 × 2 × 7 × 3 = 2142

(iii) 45, 99, 132, 165
Answer:
The given numbers are 45, 99, 132 and 165.

∴ LCM = 3 × 11 × 5 × 3 × 4 = 1980

Question 3.
Find the smelliest number which when added to 5 is exactly divisible by 12, 14 and 18.
Answer:
Let us find the LCM of 12, 14 and 18.

∴ LCM = 2 × 3 × 2 × 7 × 3 = 252
∴ The required smallest number = 252 – 5 = 247

Question 4.
Find the greatest 3 digit number which when divided by 75,45 and 60 leaves:
(i) no remainder
(ii) the remainder 4 in each case.
Answer:
(i) The given numbers are 75, 45 and 60.

∴ LCM = 5 × 3 × 5 × 3 × 4 = 900
∴The required number with no remainder = 900

(ii) The required number with
remainder 4 in each case = 900 + 4 = 904

Question 5.
Prasad and Raju met in the market on 1^st of this month. Prasad goes to the market every 3^rd day and Raju goes every 4^th day. On what day of the month will they meet again ?
Answer:
The day on which Prasad and Raju met in the market is 1^st of this month.
Prasad goes to the market every 3^rd day.
Raju goes to the market every 4^th day.
To find the day on which they meet again, we have to find the LCM of 3 and 4.
LCM of 3 and 4 = 3 × 4 = 12
So, Raju and Prasad meet again after 12 days.
(i.e.,) They meet again on 13^th day of this month.

Students can practice TS 6th Class Maths Solutions Chapter 3 Playing with Numbers Ex 3.4 to get the best methods of solving problems.

TS 6th Class Maths Solutions Chapter 3 Playing with Numbers Exercise 3.4

Question 1.
Find the HCF of the following numbers by prime factorisation and continued division method.
(i) 18, 27, 36
Answer:
The given numbers are
18, 27, 36

Prime factorisation method:

The common factor of 18, 27 and 36 is 3 × 3 = 9
Hence, HCF of 18, 27 and 36 is 9.

Continued division method :
The given numbers are 18, 27 and 36.
Let us find the HCF of 18 and 27.

∴ HCF of 18 and 27 is 9.
Let us find the HCF of third number and the HCF of first.two numbers.
Let us find the HCF of 36 and 9.

HCF of 18, 27 and 36 is 9.

(ii) 106, 159, 265
Answer:
The given numbers are 106, 159 and 265.

Prime factorisation method:

∴ The common factor of 106, 159 and 265 is 53.
Hence, HCF of 106,159 and 265 is 53.

Continued division method:
Let us find the HCF of 106 and 159.

The HCF of 106 and 159 is 53.
Let us find the HCF of 265 and 53.

Again the HCF of 265 and 53 is 53.
So, the HCF of 106, 159 and 265 is 53.

(iii) 10, 35, 40
Answer:
The given numbers are 10, 35 and 40.

Prime factorisation method:

∴ The common factor of 10, 35 and 40 is 5.
Hence, HCF of 10, 35 and 40 is 5.

Continued division method:
The given numbers are 10, 35 and 40.
Let us find the HCF of 10 and 35.

∴HCF of 10 and 35 is 5.
Let us find the HCF of third number and the HCF of first two numbers.
Let us find the HCF of 40 and 5.

∴ HCF of 40 and 5 is 5.
∴ HCF of 10, 35 and 40 is 5.

(iv) 32, 64, 96, 128
Answer:
The given numbers are 32, 64, 96 and 128.

Prime factorisation method:

∴ The common factor of 32, 64, 96 and 128 is 2 × 2 × 2 × 2 × 2 = 32
∴ HCF of 32, 64, 96 and 128 is 32.

Continued division method:
Let us find the HCF of 32 and 64.

∴ HCF of 32 and 64 is 32.
Again find the HCF of 32 and 96.

∴ HCF of 32 and 96 is 32.
Again find the HCF of 32 and 128.

∴ HCF of 32 and 128 is 32.
∴ The HCF of the given numbers is 32.

Question 2.
Find the largest number which is a factor of each of the numbers 504, 792 and 1080.
Answer:
Largest number which is a factor of the given numbers is HCF.
Let us find the HCF of 504 and 792.

∴ HCF of 72 and 1080 is 72.
The HCF of 504, 792 and 1080 is 72.

Question 3.
The length, breadth and height of a room are 12m, 15m and 18m respectively. Determine the length of longest stick that can measure all the dimensions of the room in exact number of times?
Answer:
The HCF of 12, 15 and 18 will give us the length of the stick which can measure all the three dimensions of the room exactly.

∴ HCF of 12, 15 and 18 is 3.
The length of stick is 3 m.

Question 4.
HCF of co-prime numbers 4 and 15 was found as follows by factorization. 4 = 2 × 2 and 15 = 3 × 5. Since there is no common prime factor, HCE of 4 and 15 is ‘0’. Is the answer correct? If not, what Is the correct HCF?
Answer:
The numbers which have only 1 as the common factor are called co-primes.
In the problem it is given that 4 and 15 are co-prime numbers.
∴ Their common factor is 1.
HCF of 4 and 15 is ‘0’ given in the problem. This is not correct.
The correct HCF is 1.

Question 5.
What is the capacity of the largest vessel which can empty the oil from three vessels containing 32 litres, 24 litres and 48 litres an exact number of times ?
Answer:
The quantity of oil in three vessels is 32 litres, 24 litres and 48 litres.

∴ LCM = 2 × 2 × 2 × 3 × 2 × 2 = 96
The capacity 4 the largest vessel = 96 litres.

Students can practice TS 6th Class Maths Solutions Chapter 3 Playing with Numbers Ex 3.2 to get the best methods of solving problems.

TS 6th Class Maths Solutions Chapter 3 Playing with Numbers Exercise 3.2

Question 1.
Write all the factors of the following numbers.
(i) 36
Answer:
The factors of 36 are
1, 2, 3, 4, 6, 9, 12, 18, 36.

(ii) 23
Answer:
The factors of 23 are 1 and 23.

(iii) 96
Answer:
The factors of 96 are
1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96

(iv) 115
Answer:
The factors of 115 are 1, 5, 23, 115

Question 2.
Which of the following pairs are co-prime ?
(i) 16 and 35
Answer:
The factors of 18 are 1, 2, 3, 6, 9, 18.
The factors of 35 are 1, 5, 7, 35.
The common factor for both 18 and 35 is 1 only.
∴ 18 and 35 are co-primes.

(ii) 216 and 215
Answer:
The factors of 216 are 1,2,3,4,9,24, 36, 54, 72, 108,216.
The factors of 215 are 1, 5, 43.
The common factor for both 216 and 215 is 1 only.
∴ 216 and 215 are co-primes.

(iii) 30 and 415
Answer:
The factors for 30 are
1, 2, 3, 5, 6, 10, 15, 30.
The factors for 415 are 1, 5, 83.
The common factors for both 30 and 415 are 1, 5.
They have two common factors.
∴ 30 and 415 are not co-primes.

(iv) 17 and 68
Answer:
The factors for 17 are 1,17.
The factors for 68 are 1, 2, 4, 17, 34, 68.
The common factor for both 17 and 68 is 1 only.
∴ 17 and 68 are co-primes.

Question 3.
What is the greatest prime number between 1 and 20 ?
Answer:
The prime numbers between 1 and 20 are 2, 3,5, 7, 11,13, 17, 19.
∴ The greatest prime number is 19.

Question 4.
Find the prime ‘ and composite numbers between 10 and 30 ?
Answer:
The prime numbers between 10 and 30 are 11, 13, 17, 19, 23, 29.
The composite numbers between 10 and 30 are 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28.

Question 5.
The numbers 17 and 71 are prime numbers. Both these numbers have same digits 1 and 7. Find 2 more such pairs of prime numbers below 100.
Answer:
13 and 31; 37 and 73 are two pairs of prime numbers.

Question 6.
Write three pairs of twin primes below 20?
Answer:
(3, 5); (5, 7); (11, 13) are twin primes.

Question 7.
Write two prime numbers whose product is 35.
Answer:
The two prime numbers whose product is 35 are 5 and 7.

Question 8.
Express 36 as the sum of two odd primes.
Answer:
The two odd primes whose sum is 36 are 13 and 23.
∴ 36 = 13 + 23

Question 9.
Write seven consecutive composite numbers less than 100.
Answer:
4, 6, 8, 10, 12, 14 and 16

Question 10.
Express 53 as the sum of three primes.
Answer:
53 = 3 + 19 + 31

Question 11.
Write two prime numbers whose difference is 10.
Answer:
19 and 29. (∵ 29 – 19 = 10)

Question 12.
Write three pairs of prime numbers less than 20 whose sum is divisible by 5?
Answer:
(3, 7), (7, 13), (17, 3)
These pairs of prime numbers are less than 20. The sum of each pair is divisible by 5.

Students can practice TS 6th Class Maths Solutions Chapter 3 Playing with Numbers Ex 3.1 to get the best methods of solving problems.

TS 6th Class Maths Solutions Chapter 3 Playing with Numbers Exercise 3.1

Question 1.
Which of the following numbers are divisible by 2, by 3 and by 6 ?
(i) 321729
Answer:
The given number is 321729.
Since 9 is in units place, it is not divisible by 2.
Sum of the digits = 3 + 2 + 1 + 7 + 2 + 9 = 24 (a multiple of 3)
So, it is divisible by 3.
∴ The given number is not divisible by 6 as it is not divisible by 2.

(ii) 197232
Answer:
The given number is 197232.
Since 2 is in units place, it is divisible by 2.
Sum of the digits = l+ 9 + 7 + 2 + 3 + 2 = 24 (a multiple of 3)
So, it is divisible by 3.
∴ The given number is divisible by 6 because it is divisible by both 2 and 3.

(iii) 972132
Answer:
The given number is 972132.
Since 2 is in units place, it is divisible by 2.
Sum of the digits = 9 + 7 + 2 + 1 + 3 + 2 = 24 (a multiple of 3)
So, it is divisible by 3.
∴ The given number is divisible also because it is divisible by both 2 and 3.

(iv) 1790184
Answer:
The given number is 1790184.
Since 4 is in units place, it is divisible by 2.
Sum pf the digits = 1 + 7 + 9 + 0 + 1 + 8 + 4 = 30 (a multiple of 3)
So, it is divisible by 3.
∴The given number is divisible by 6 also because it is divisible by both 2 and 3.

(v) 312792
Answer:
The given number is 312792.
Since 2 is in units place, it is divisible by 2.
Sum of the digits = 3 + 1 + 2 + 7 + 9 + 2 = 24 (a multiple of 3) So, it is divisible by 3.
∴ The given number is divisible by 6 also because it is divisible by both 2 and 3.

(vi) 800552
Answer:
The given number is 800552
Since 2 is in units place, it is divisible by 2.
Sum of the digits = 8 + 0 + 0 + 5 + 5 + 2 = 20 (not a multiple of 3)
∴ The given number is not divisible by 3.
∴ The given number is divisible by 2 but not by 3.
So, it is not divisible by 6.

(vii) 4335
Answer:
The given number is 4335.
Since 5 is in units place, it is not divisible by 2.
Sum of the digits = 4 + 3 + 3 + 5 = 15 (a multiple of 3)
So, it is divisible by 3.
∴ The given number is divisible by 3 but not by 2.
So, it is not divisible by 6.

(viii) 726352
Answer:
The given number is 726352.
Since 2 is in units place, it is divisible by 2.
Sum of the digits = 7 + 2 + 6 +3 + 5 + 2 = 25 (not a multiple of 3)
So, it is not divisible by 3.
∴ The given number is divisible by 2 but not by 3.
So, it is not divisible by 6.

Question 2.
Determine which of the following numbers are divisible by 5 and by 10. 25,125,250,1250,10205,70985,45880. Check whether the numbers that are divisible by 10 are also divisible by 2 and 5.
Answer:
Since ‘5’ or ‘0’ is in units place of the above given numbers, they are divisible by 5.
The numbers having ‘0’ in units place (i.e.,)
250, 1250, 45880 are divisible by 10.
250 is divisible by 2 and also by 5. (∵ If ‘0’ is in units place, it is divisible by 2 and by 5).
So, the other two numbers (i.e.,) 1250 and 45880 are also divisible by 2 and by 5.

Question 3.
Fill the table using divisibility test for 3 and 9.

Answer:

Question 4.
Make 3 different 3 digit numbers using 1, 9 and 8, where each digit can be used only once. Check which of these numbers are divisible by 9.
Answer:
The 3 different 3 digit numbers using 1, 9 and 8 are 981, 819, 198
Sum of the digits in 981 = 9 + 8 + 1 = 18
18 is divisible by 9. So the number 981 is also divisible by 9.
Sum of the digits in 819 = 8 + 1 + 9 = 18
Sum of the digits in 198 = 1 + 9 + 8 = 18
So these .two numbers (i.e.,) 819 and 198 are also divisible by 9.
(∵ 18 is divisible by 9)

Question 5.
Which numbers among 2, 3, 5, 6, 9 divides 12345 exactly ?
Write 12345 in reverse order and test now which numbers divide it exactly ?
Answer:
(i) 2 does not divide 12345 exactly.
3 divides 12345 exactly.
(∵ Sum of the digits 1 + 2 + 3 + 4 + 5 = 15isa multiple of ‘3’)
5 divides 12345 exactly.
(∵ 5 is in units place)
6 does not divide 12345 exactly
(∵ 12345 is divisible by 3 but not by 6)
9 does not divide 12345 exactly.
(∵ Sum of the digits (i.e.,) 15 is not divisible by 9)

(ii) 2,5, 6, 9 does not divide 54321 exactly.
(iii) 3 divides 54321 exactly.
∴ Sum of the digits is 5 + 4 + 3 + 2 + 1 = 15 is a multiple of 3.

Question 6.
Write different 2 digit numbers using digits 3, 4 and 5. Check whether these numbers are divisible by 2, 3, 5, 6 and 9.
Answer:
The two digit numbers formed with 3, 4 and 5 are 34, 35, 45, 43, 53, 54.
34 is divisible by 2. .
35 is divisible by 5.
45 is divisible by 3, 5 and 9.
43 is not divisible by 2, 3, 5, 6 or 9.
53 is not divisible by 2, 3, 5, 6 or 9.
54 is divisible by 2, 3, 6 and 9.

Question 7.
Write the smallest digit and the great-est possible digit in the blank space of each of the following numbers so that the number formed are divisible by 3.
(i) …………………… 6724
(ii) 4765 ……………………. 2
(iii) 7221 …………………….. 5
Answer:
(i) 2 6724 and 56724
(ii) 476532 and 476592
(iii) 722145 and 722175

Question 8.
Find the smallest number that must be added to 123, so that it becomes exactly divisible by 5.
Answer:
The given number is 123.
The digit in ones place should be 5 so that it becomes exactly divisible by 5.
∴ 2 is to be added to 123.
Then the number becomes
123 + 2 = 125, divisible by 5.

Question 9.
Find the smallest number that has to be subtracted from 256, so that it becomes exactly divisible by 10.
Answer:
The given number is 256.
The digit in units place should be ‘0’ so that it becomes exactly divisible by 10.
6 has to be subtracted from 256. Then the number becomes 256 – 6 = 250 which is exactly divisible by 10.

Students can practice TS 6th Class Maths Solutions Chapter 4 Basic Geometrical Ideas InText Questions to get the best methods of solving problems.

TS 6th Class Maths Solutions Chapter 4 Basic Geometrical Ideas InText Questions

Do This

Question 1.
Four points are marked in the given rectangle. Name them.

Answer:
Their names taken as P, Q, R, S.

Question 2.
Take a geo-board. Select any two nails and tie tightly a thread from one end to the other. The thread you have fixed is a line which can extend in both directions and only in these two directions.

Answer:
Student activity

Think: Discuss And Write

Question 1.
Here is a ray \(\overrightarrow{\mathrm{O A}}\). It starts at O and passes through the points A and B.
Can you name ray \(\overrightarrow{\mathrm{O A}}\) as \(\overrightarrow{\mathrm{O B}}\)? Why?

Can you write the ray \(\overrightarrow{\mathrm{O A}}\) as \(\overrightarrow{\mathrm{A O}}\) ? Why ? Give reasons.
Answer:

The above ray starts from the point ‘O’ towards B so, it is named as \(\overrightarrow{\mathrm{O B}}\).
\(\overrightarrow{\mathrm{OA}} \neq \overrightarrow{\mathrm{AO}}\) since the ray starts from 0 i.e., it should be represented by only \(\overrightarrow{\mathrm{O A}}\).

Think. Discuss And Write

Question 1.
Move your pencil along the following English letters and state which are open and which are closed?

Answer:
D and O are closed letters
G, L, M are open letters.

Question 2.
Tell which letter is an example of simple curve.
Answer:
O is an example of simple curve.

Try These

Question 1.
Identify which are simple curves and which are not?

Answer:
(i) and(ii) are simple curves.
(iii) and (iv) are not simple curves.

Do This

Question 1.
Take some match sticks and try to make simple figures. Identify closed figures in them.
Answer:

Question 2.

What is the least number of sticks needed to form a closed figure ? Obviously three. Can you explain why two match sticks can not make a closed figure.
Answer:
Minimum number of sticks that are needed to form a closed figure are 3. If we take less than 3 sticks it will become a open figure.

Question 3.
Take some straw pieces of diffrent size. Pass thread into any 3 pieces and make different triangles. Draw figures for the tiangles in your notebook.
Answer:

Think, Discuss And Write

Question 1.
Take four points A, B, C and D such that A, B, C lie on the same line and D is not on it. Can the four line segments \(\overline{\mathrm{A B}}, \overline{\mathrm{B C}}, \overline{\mathrm{C D}}\) and \(\overline{\mathrm{AD}}\) form a quadrilateral? Give reason.

Answer:

No, the given four line segments \(\overline{\mathrm{A B}}, \overline{\mathrm{B C}}, \overline{\mathrm{C D}}\) and \(\overline{\mathrm{AD}}\)
Can not form a quadrilateral.
To form a quadrilateral maximum two points should be collinear.

Do This

Question 1.
Draw a circle on a paper and cut ¡t along its edge. Fold it Into half and again fold it to one fourth to make folding marks as shown.

You will observe a point in the middle. Mark this O. This is the centre of the circle. You can also indicate its radius. How many radii can you draw in a circle ?
Answer:

Infinite number of radii we can draw in a circle.
Because infinite number of points are there on the circumference of the circle.

Question 2.
Draw a circle and draw at least 5 chords in it. Make sure at least one of them passes through the centre. Name them and fill the table.

What do you notice?
Answer:

I notice that a chord which passes through the centre of the circle is the largest chord of all the chords.

Think And Discuss

Question 1.
Is it possible to draw more than one diameter in a circle ? Are all the diameters equal in length ? Discuss with your friends and find the answer.
Answer:
We can draw infinite number of diameters in a circle.

All the lengths of diameters are equal in a circle.
Since \(\overline{\mathrm{AF}}=\overline{\mathrm{BG}}=\overline{\mathrm{CH}}\) = 2.5 cm

Students can practice TS 6th Class Maths Solutions Chapter 3 Playing with Numbers Ex 3.3 to get the best methods of solving problems.

TS 6th Class Maths Solutions Chapter 3 Playing with Numbers Exercise 3.3

Question 1.
Write the missing numbers in the factor tree for 90.
(i.)

Answer:

(ii)

Answer:

Question 2.
Factorise 84 by division method.
Answer:

∴ 84 = 2 × 2 × 3 × 7 × 1

Question 3.
Write the greatest 4 digit number and express it in the form of it’s prime factors.
Answer:
The greatest 4 digit number is 9999

∴ 9999 = 3 × 3 × 11 × 101

Question 4.
I am the smallest number, having four different prime’ factors. Can you find me ?
Answer:
The smallest number, having four different prime factors is
2 × 3 × 5 × 7
(i.e.) 210.

Students can practice TS 6th Class Maths Solutions Chapter 2 Whole Numbers Ex 2.3 to get the best methods of solving problems.

TS 6th Class Maths Solutions Chapter 2 Whole Numbers Exercise 2.3

Question 1.
Study the pattern:
1 × 8 + 1 = 9
12 × 8 + 2 = 98
123 × 8 + 3 = 987
1234 × 8 + 4 = 9876
12345 × 8 + 5 = 98765
Write the next four steps. Can you find out how the pattern works?
Answer:
123456 × 8 + 6 = 987654 .
1234567 × 8 + 7 = 9876543
12345678 × 8 + 8 = 98765432
123456789 × 8 + 9 = 987654321

Working pattern is as follows:
1) Write the smallest of the natural numbers, multiply it by 8 and add 1 to product obtained. You get a single digit number (i.e.) 9. i.e., 1 × 8 + 1 = 9

2) Write the number formed by the first two natural numbers in the same order, multiply it by 8 and add 2 to the product obtained. You get a two digit number with 9 tens place and the next digit (succeeding digit) decreases by 1.
i.e., 12 × 8 + 2 = 98

3) Write the number formed by the first three natural numbers in the same order, multiply it by 8 and add 3 to the product obtained. You get a three digit number with 9 in hundreds place and the next two digits gradually decrease by 1,
i.e., 123 × 8 + 3 = 987 and so on.

Question 2.
Study the pattern:
91 × 11 × 1 = 1001
91 × 11 × 2 = 2002
91 × 11 × 3 = 3003
Write next seven steps. Check, whether the result is correct.
Try the pattern for 143 × 7 × 1, 143 × 7 × 2 ………..
Answer:
91 × 11 × 4 = 4004
91 × 11 × 5 = 5005
91 × 11 × 6 = 6006
91 × 11 × 7 = 7007
91 × 11 × 8 = 8008
91 × 11 × 9 = 9009
91 × 11 × 10= 10010

Verification :
91 × 11 × 4 = 91 × 44
= 91 × (40 + 4)
= (91 × 40) + (91 × 4)
= 3640 + 364
= 4004

143 × 7 × 1 = 1001
143 × 7 × 2 = 2002
143 × 7 × 3 = 3003
143 × 7 × 4 = 4004
143 × 7 × 5 = 5005

Question 3.
How would we multiply the numbers 13680347, 35702369 and 25692359 with 9 mentally? What is the pattern that emerges.
Answer:
(i) 13680347 × 9 = 13680347 × (10 – 1)
= 13680347 × 10 – 13680347 × 1
= 136803470 – 13680347
= 123123123

(ii) 35702369 × 9 = 35702369 × (10 – 1)
= 35702369 × 10 – 35702369 × 1
= 357023690 – 35702369
= 321321321

(iii) 25692359 × 9
= 25692359 × (10 – 1)
= 25692359 × 10 – 25692359 × 1
= 256923590 – 25692359
= 231231231
Working pattern : If any number is to be multiplied by 9, first multiply the given number by 10 (write ‘0’ at the end of the number) and subtract the given number from the product obtained. (∴ 9 = 10-1)

Students can practice TS 6th Class Maths Solutions Chapter 1 Knowing Our Numbers Ex 1.2 to get the best methods of solving problems.

TS 6th Class Maths Solutions Chapter 1 Knowing Our Numbers Exercise 1.2

Question 1.
Round off the following numbers to the nearest tens.
(i) 89
Answer:
89 is nearer to 90 than 80. So it is rounded off to 90

(ii) 415
Answer:
415 is at equal distance from 410 and 420 but by convention it is rounded off to 420.

(iii) 3951
Answer:
3951 is nearer to 3950 than 3960. So it is rounded off to 3950.

(iv) 4409
Answer:
4409 is nearer to 4410 than 4400. So it is rounded off to 4410.

Question 2.
Round off the following numbers to the nearest hundreds.
(i) 695
Answer:
695 is nearer to 700 than 600. So it is rounded off to 700.

(ii) 36152
Answer:
36152 is nearer to 36200 than 36100. So it is rounded off to 36200.

(iii) 13648
Answer:
13648 is nearer to 13600 than 13700. So it is rounded off to 13600.

(iv) 93618
Answer:
93618 is nearer to 93600 than 93700. So it is rounded off to 93600.

Question 3.
Round off the following numbers to the nearest thousands.
(i) 03415
Answer:
3415 is nearer to 3000 than 4000. So it is rounded off to 3000.

(ii) 70124
Answer:
70124 is nearer to 70000 than 71000. So it is rounded off to 70000.

(iii) 8765
Answer:
8765 is nearer to 9000 than 8000. So it is rounded off to 9000.

(iv)4001
Answer:
4001 is nearer to 4000 than 5000. So it is rounded off to 4000.

Question 4.
Write the numbers in short form.
(i) 3000 + 400 + 7
Answer:
3000 + 400 + 7 = 3407

(ii) 10000 + 2000 + 300 + 50 + 1
Answer:
10000 + 2000 + 300 + 50 + 1 = 12351

(iii) 30000 + 500 + 20 + 5
Answer:
30000 + 500 + 20 + 5 = 30525

(iv) 90000 + 9000 + 900 + 90 + 9
Answer:
90000 + 9000 + 900 + 90 + 9 = 99999

Question 5.
Write the expanded form of the numbers.
(i) 4348
Answer:
4348 = (4 × 1000) + (3 × 100) + (4 × 10) + (8 × 1)
= 4000 + 300 + 40 + 8

(ii) 30214
Answer:
30214 = (3 × 10000) + (2 × 100) + (1 × 10) + (4 × 1)
= 30000 + 200 + 10 + 4

(iii) 22222
Answer:
22222 = (2 × 10000) + (2 × 1000) + (2 × 100) + (2 × 10) + (2 × 1)
= 20000 + 2000 + 200 + 20 + 2

(iv) 75025
Answer:
75025 = (7 × 10000) + (5 × 1000) + (2 × 10) + (5 × 1)
= 70000 + 5000 + 20 + 5

Students can practice TS 6th Class Maths Solutions Chapter 2 Whole Numbers Ex 2.2 to get the best methods of solving problems.

TS 6th Class Maths Solutions Chapter 2 Whole Numbers Exercise 2.2

Question 1.
Give the results without actually performing the operations using the given information.
(i) 28 × 19 = 532 then 19 × 28 =
(ii) 1 × 47 = 47 then 47 × 1 =
(iii) a × b = c then b × a =
(iv) 58 + 42 = 100 then 42 + 58 =
(v) 85 + 0 = 85 then 0 + 85 =
(vi) a + b = d then b + a =
Answer:
(i) 28 × 19 = 532 then 19 × 28 = 532
(ii) 1 × 47 = 47 then 47 × 1 = 47;
(iii) a × b = c then b × a = c
(iv) 58 + 42 = 100 then 42 + 58 = 100
(v) 85 + 0 = 85 then 0 + 85 = 85
(vi) a + b = d then b + a = d

Question 2.
Find the sum by suitable rearrangement:
(i) 238 + 695 + 162
Answer:
238 + 695 + 162 = (238 + 162) + 695
= 400 + 695 = 1095

(ii) 154 + 197 + 46 + 203
Answer:
154 + 197 + 46 + 203
= (154 + 46) + (197 + 203) = 200 + 400 = 600

Question 3.
Find the product by suitable rearrangement.
(i) 25 × 1963 × 4
Answer:
25 × 1963 × 4 = (25 × 4) × 1963
= 100 × 1963
= 196300

(ii) 20 × 255 × 50 × 6
Answer:
20 × 255 × 50 × 6 = (20 × 50) × (255 × 6)
= 1000 × 1530
= 1530000

Question 4.
Find the value of the following:
(i) 368 × 12 + 18 × 368
Answer:
(368 × 12) + (18 × 368)
= 368 × [12 + 18]
= 368 × 30
= 11040

(ii) 79 × 4319 + 4319 × 11
Answer:
(79 × 4319) + (4319 × 11)
= 4319 × [79 + 11]
= 4319 × 90
= 388710

Question 5.
Find the product using suitable properties:
(i) 205 × 1989
Answer:
1989 × 205 = 1989 × (200 + 5) = (1989 × 200) + (1989 × 5)
= 397800 + 9945 = 407745

(ii) 1991 × 1005
Answer:
1991 × 1005 = 1991 × [1000 + 5] = (1991 × 1000) + (1991 × 5)
= 1991000 + 9955 = 2000955

Question 6.
A milk vendor supplies 56 liters of milk in the morning and 44 liters of milk in the evening to a hostel. If the milk costs ₹ 30 per liter, how much money he gets per day?
Answer:
Quantity of milk supplied to the hostel in the morning = 56 litres
Quantity of milk supplied to the hostel in the evening = 44 litres
Quantity of milk supplied to the hostel per day = (56 + 44) litres = 100 litres
Cost of 1 litre of milk = ₹ 30
Cost of 100 litres of milk = ₹ 30 × 100 = ₹ 3000

Question 7.
Chandana and Venu purchased 12 note books and10 note books respectively. The cost of each note book is ₹ 15,then how much amount should they pay to the shop keeper?
Answer:
Cost of one note book = ₹ 15
Number of note books that Chandana bought =12
Amount that Chandana has to pay the shopkeeper = ₹ 15 × 12
Number of notebooks that Venu bought = 10
Amount that Venu has to pay to the shopkeeper = ₹ 15 × 10
Total amount that Chandana and Venu have to pay the shopkeeper =
₹ 15 × 12 + ₹ 15 × 10 = ₹ 15 [12 + 10] = ₹ 15 × 22 = ₹ 330

Question 8.
Match the following:

Answer:

Students can practice TS 6th Class Maths Solutions Chapter 1 Knowing Our Numbers Ex 1.4 to get the best methods of solving problems.

TS 6th Class Maths Solutions Chapter 1 Knowing Our Numbers Exercise 1.4

Question 1.
Write the numbers using commas according to International system of numeration.
(i) 97645315
Answer:
97,645,315

(ii) 20048421
Answer:
20,048,421

(iii) 476356
Answer:
476,356

(iv) 9490026834
Answer:
9,490,026,834

Question 2.
Collect the mobile numbers of your friends and other family members. Write them using commas and read them in International system.
Answer:
1. 9,912,342,343
Nine billion nine hundred twelve mil-lion three hundred forty two thou-sand three hundred forty three.

2. 9,989,857,886
Nine billion nine hundred eighty nine million eight hundred fifty seven thousand eight hundred eighty six.

3. 9,849,258,633
Nine billion eight hundred forty nine million two hundred fifty eight thou-sand six hundred thirty three.

4. 9,032,050,053
Nine billion thirty two million fifty thousand fifty three.

5. 9,490,605,604
Nine billion four hundred ninety million six hundred five thousand six hundred four.

6. 9,440,824,201
Nine billion four hundred forty million eight hundred twenty four thousand two hundred one.

7. 9,949,584,445
Nine billion nine hundred forty nine million five hundred eighty four thousand four hundred forty five.

8. 9,848,212,356
Nine billion eight hundred forty eight million two hundred twelve thousand three hundred fifty six.

9. 9,440,172,042
Nine billion four hundred forty million one hundred seventy two thousand forty two.

10. 9,989,027,829
Nine billion nine hundred eighty nine million twenty seven thousand eight hundred twenty nine.

Question 3.
Write the numbers in words in both Indian and International system.
(i) 123115027
Answer:
Indian system: 12,31,15,027
Twelve crores thirty one lakh fifteen thousand twenty seven.

International system: 123,115,027 One hundred twenty three million one hundred fifteen thousand twenty seven.

(ii) 89643092
Answer:
Indian system: 8,96,43,092
Eight crores ninety six lakh forty three thousand ninety two.

International system: 89,643,092 Eighty nine million six hundred forty three thousand ninety two.

Question 4.
Read the number carefully and answer the following:
302,179,468
(i) The digit in millions place.
Answer:
The digit in millions place is 2.

(ii) The digit in hundreds place.
Answer:
The digit in hundreds place is 4.

(iii) The digit in ten millions place.
Answer:
The digit in ten millions place is 0.

(iv) How many millions are there in the number ?
Answer:
302 millions are there in the number.