TS 6th Class Maths Solutions Chapter 3 Playing with Numbers Ex 3.5

Students can practice TS 6th Class Maths Solutions Chapter 3 Playing with Numbers Ex 3.5 to get the best methods of solving problems.

TS 6th Class Maths Solutions Chapter 3 Playing with Numbers Exercise 3.5

Question 1.
Find the LCM of the following numbers by prime factorisation method.
(i) 12 and 15
Answer:
The given numbers are 12 and 15.
Let us e×press each number as a product of prime factors.

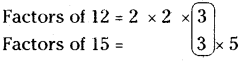
The common factor of both = 3
Take the extra factors of both 12 and 15, (i.e.,) 2, 2 and 5
∴ LCM = 2 × 2 × 5 × 3 = 60

(ii) 15 and 25
Answer:
The given numbers are 15 and 25.
Let us express each number as the product of prime factors.

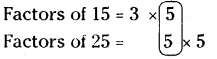
The common factor of both = 5
The extra factors of both = 3 and 5
∴ LCM = 3 × 5 × 5 = 75.

(iii) 14 and 21
Answer:
The given numbers are 14 and 21.
Let us express each number as the product of prime factors.

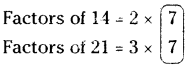
The common factor of both = 7
The extra factors of both = 2 and 3
∴ LCM = 2 × 3 × 7 = 42

(iv) 18 and 27
Answer:
The given numbers are 18 and 27
Let us express each number as the product of prime factors.

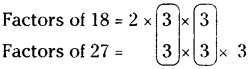
The common factor of both = 3 × 3
The extra factors of both = 2 and 3
∴ LCM = 3 × 3 × 2 × 3 = 54

(v) 48, 56 and 72
Answer:
The given numbers are 48, 56 and 72.
Let us express each number as the product of prime factors.

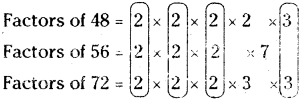
The common factor of the three numbers = 2 × 2 × 2 × 3
The extra factors of the three numbers = 2 × 3 × 7
∴ LCM = 2 × 2 × 2 × 3 × 2 × 3 × 7 = 1008

(vi) 26, 14 and 91
Answer:
The given numbers are 26, 14 and 91
Let us express each number as the product of prime factors

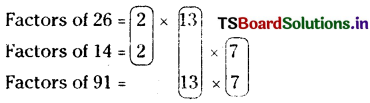
The common factors of the three numbers = 2 × 13 × 7
There are no extra factors of all the numbers.
∴ LCM = 2 × 13 × 7 = 182

Question 2.
Find the LCM of the following numbers by division method,
(i) 84, 112, 196
Answer:
The given numbers are 84, 112 and 196.

∴ LCM = 2 × 2 × 7 × 3 × 4 × 7 = 2352

(ii) 102, 119, 153
Answer:
The given numbers are 102, 119 and 153.

∴ LCM = 17 × 3 × 2 × 7 × 3 = 2142

(iii) 45, 99, 132, 165
Answer:
The given numbers are 45, 99, 132 and 165.

∴ LCM = 3 × 11 × 5 × 3 × 4 = 1980

Question 3.
Find the smelliest number which when added to 5 is exactly divisible by 12, 14 and 18.
Answer:
Let us find the LCM of 12, 14 and 18.

∴ LCM = 2 × 3 × 2 × 7 × 3 = 252
∴ The required smallest number = 252 – 5 = 247

Question 4.
Find the greatest 3 digit number which when divided by 75,45 and 60 leaves:
(i) no remainder
(ii) the remainder 4 in each case.
Answer:
(i) The given numbers are 75, 45 and 60.

∴ LCM = 5 × 3 × 5 × 3 × 4 = 900
∴The required number with no remainder = 900

(ii) The required number with
remainder 4 in each case = 900 + 4 = 904

Question 5.
Prasad and Raju met in the market on 1^st of this month. Prasad goes to the market every 3^rd day and Raju goes every 4^th day. On what day of the month will they meet again ?
Answer:
The day on which Prasad and Raju met in the market is 1^st of this month.
Prasad goes to the market every 3^rd day.
Raju goes to the market every 4^th day.
To find the day on which they meet again, we have to find the LCM of 3 and 4.
LCM of 3 and 4 = 3 × 4 = 12
So, Raju and Prasad meet again after 12 days.
(i.e.,) They meet again on 13^th day of this month.