TS Inter 2nd Year Maths 2B Hyperbola Important Questions

Students must practice these TS Inter 2nd Year Maths 2B Important Questions Chapter 5 Hyperbola to help strengthen their preparations for exams.

TS Inter 2nd Year Maths 2B Hyperbola Important Questions

Short Answer Type Questions

Question 1.
If e, e₁ are the eccentricities of a hyperbola and its conjugate hyperbola, prove that \(\frac{1}{e^2}+\frac{1}{e_1^2}=1\)
Solution:
Let e, e₁ be the eccentricities of hyperbola

Question 2.
Find the equations of the tangents to the hyperbola 3x² – 4y² = 12 which are (I) parallel and (H) perpendicular to the line y = x – 7.
Solution:
Equation of given hyperbola is \(\frac{x^2}{4}-\frac{y^2}{3}=1\)
So that a² = 4, b² = 3 and equation to the given line y = x  – 7 and slope is ‘1’.

(i) Slope of the tangents which are parallel to the given line is ‘1’.
∴ Equation of tangents are
y = mx ± \(\sqrt{a^2 m^2-b^2}\)
⇒ y=x± \(\sqrt{4-3}\) and
⇒ y = x ± 1

(ii) Slope of the tangent which are perpendicular to the given line is – 1.
∴ Equations of tangents which are perpendicular to the given line are
y = (-1) x ± \(\sqrt{4(-1)^2-3}\)
x+y = ±1

Question 3.
A circle on the rectangular hyperbola xy = 1. In the points (Xr Yr)’ (r = 1, 2, 3, 4) Prove that x₁ x₂ x₃ x₄ = y₁ y₂ y₃ y₄ = 1.
Solution:
Let the circle be x² + y² = a².
Since \((\mathrm{t}, \frac{1}{t})\)(t ≠ 0) lies on xy= 1, the points of intersection of the circle and the hyperbola are given by
\(t^2+\frac{1}{t^2}=a^2\)

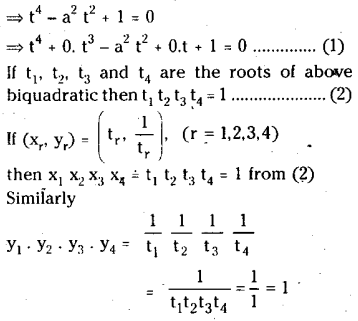
Long Answer Type Questions

Question 1.
Find the centre, eccentricity, foci, directrices and the length of latus rectum of the following hyperbolas.
4x² – 9y² – 8x -32 = 0
Solution:
Given equation is 4x² – 9y² –  8x – 32 = 0
⇒ 4x² – 8x -9y² = 32
⇒ 4(x -2x)-9y=32
⇒ 4(x²-2x+ 1) – 9y² = 32 + 4 = 36
⇒ 4 (x-1)2 – 9y² = 36
\(\frac{(x-1)^2}{9}-\frac{(y-0)^2}{4}=1\)
∴ Centre of the hyperbola = (1, 0)
The semi-transverse axis a = 3, and the semiconjugate axis b = 2.
∴ \(e=\sqrt{\frac{a^2+b^2}{a^2}}=\sqrt{\frac{9+4}{9}}=\sqrt{\frac{13}{3}}\)
Coordinates of foci (h ± ae, k)

(ii) 4(y+3)² -9(x-2)²= 1
Solution:
The equation can be written as

Question 2.
(i) If t be line lx+ my+n= 0 is a tangent to the hyperbola \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) then show that
a²l² – b²m² = n²

(ii) If the lx + my = t is a normal to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) then show that
\(\frac{a^2}{l^2}-\frac{b^2}{m^2}=\left(a^2+b^2\right)^2\)
Solution:
(i) Let the line lx + my + n = 0 ……………….. (1) is a tangent to the hyperbola S = \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) at P(θ).
Then the equation of tangent at P(θ) is
\(\frac{x}{a}\) secθ – \(\frac{x}{b}\) tanθ – 1 = θ ………….. (2)
Since (1) and (2) represent the same line,

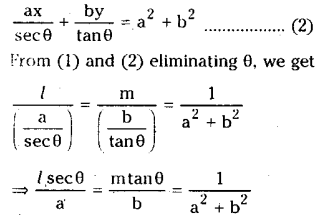
Question 3.
Prove that the point of intersection of two per perpendicular tangents to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) lies on the circle x +y =a – b.
Solution:
Let P (x₁, y₁) be a point of intersection of two perpendicular tangents to the hyperbola
The equation of any tangent to S = 0 is of the form
\(S \equiv \frac{x^2}{a^2}-\frac{y^2}{b^2}-1=0\)
The equation of any tangent to S = 0 is of the form

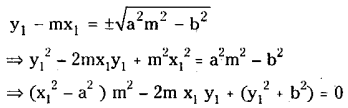
This is a quadratic equation ¡n ‘m’ which has two roots m₁, m₂ (say) which corresponds to slopes of tangents.

Question 4.
If your points be taken on a rectangular hyperbola such that the chords joining any two points is perpendicular to the chord Joining the other two, and if α , β , γ and δ be the inclinations to either asymptote of the straight lines joining these points to the centre, prove that tanα, tanβ, tanγ , tanδ = 1
Solution:
Let the equation of rectangular hyperbola be x² – y² = a². By rotating the X – axis and Y – axis about the orgin through an angle \(\frac{\pi}{4}\) in the clockwise direction the equation x² – y² = a² will be transformed to xy = C².

Since \(\overline{\mathrm{AB}}\) is perpendicular \(\overline{\mathrm{CD}}\) we have
\(\left(-\frac{1}{t_1 t_2}\right)\left(-\frac{1}{t_3 t_4}\right)=-1\)
⇒ t₁ t₁ t₁ t₁ = – 1 ………………. (1)
We have the coordinate axis as the a asymptotes of the curves.
If \(\overline{\mathrm{OA}}, \overline{\mathrm{OB}}, \overline{\mathrm{OC}}, \overline{\mathrm{OD}}\) make angles α, β, γ and δ with positive direction of X-axis then tanα, tanβ, tanγ, and tanδ are the slopes.

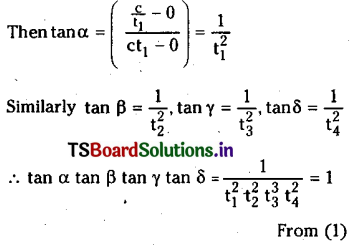
If \(\overline{\mathrm{OA}}, \overline{\mathrm{OB}}, \overline{\mathrm{OC}}, \overline{\mathrm{OD}}\) make angles α, β, γ and δ with the other asymptote the Y – axis then cot α, cot β, cot γ, cot δ are the respective slopes.
So that cot α cot β cot γ cot δ = tan α tan β tan γ tan δ = I