TS Inter 1st Year Maths 1B Solutions Chapter 9 Differentiation Ex 9(a)

Students must practice these TS Inter 1st Year Maths 1B Study Material Chapter 9 Differentiation Ex 9(a) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1B Differentiation 9(a)

I.
Question 1.
Find the derivatives of the following functions f(x). (V.S.A.Q.)
(i) √x + 2x^3/4 + 3x^5/6 (x > 0)
Answer:

(ii) \(\sqrt{2 x-3}+\sqrt{7-3 x}\)
Answer:

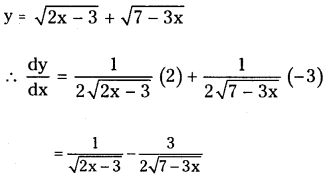
(iii) (x² – 3) (4x³ + 1)
Answer:
y = (x² – 3) (4x³ + 1)
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = (x² – 3) \(\frac{\mathrm{d}}{\mathrm{dx}}\) (4x³ + 1) + (4x³ + 1) \(\frac{\mathrm{d}}{\mathrm{dx}}\) (x² – 3)
= (x² – 3) (12x²) + (4x³ + 1) (2x)
= 12x⁴ – 36x² + 8x⁴ + 2x = 20x⁴ – 36x² + 2x

(iv) (√x – 3x) (x + \(\frac{1}{x}\))
Answer:

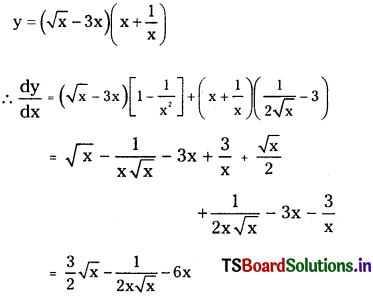
(v) (√x + 1) (x² – 4x + 2) (x > 0)
Answer:
y = (√x + 1) (x² – 4x + 2)
\(\frac{d y}{d x}\) = (√x + 1) \(\frac{d}{d x}\) (x² – 4x + 2) + (x² – 4x + 2) \(\frac{d}{d x}\) (√x + 1)
= (√x + 1) (2x – 4) + (x² – 4x + 2) \(\left(\frac{1}{2 \sqrt{x}}\right)\)
= (√x + 1) (2x – 4) + \(\frac{x^2-4 x+2}{2 \sqrt{x}}\)

(vi) (ax + b)ⁿ (cx + d)^m
Answer:
Let y = (ax + b)ⁿ (cx + d)^m
\(\frac{d y}{d x}\) = (ax + b)ⁿ . m(cx + d)^{m – 1}(c) + (cx + d)^m n (ax + b)^{n – 1} (a)
= (ax + b)ⁿ (cm (cx + d)^{m – 1}] + (cx + d)^m [an(ax + b)^{n – 1}]
= (ax + b)^{n – 1} (cx + d)^{m – 1} [cm (ax + b) + an(cx + d)]
= (ax + b)ⁿ (cx + d)^m \(\left[\frac{a n}{a x+b}+\frac{c m}{c x+d}\right]\)

(vii) 5 sin x + e^x log x
Answer:
y = 5 sin x + e^x log x

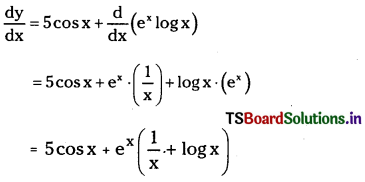
(viii) 5^x + log x + x³ e^x
Answer:
y = 5^x + log x + x³ e^x
∴ \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 5^x log 5 + \(\frac{1}{x}\) + [x³e^x + 3x²e^x]

(ix) e^x + sin x cos x
Answer:
y = e^x + sin x cos x
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = e^x + sin x (- sin x) + cos x (cos x) dx
= e^x + cos² x – sin² x = e^x + cos 2x

(x) \(\frac{p x^2+q x+r}{a x+b}\) (|a| + |b| ≠ 0)
Answer:

(xi) log₇(log x) (x > 0)
Answer:
y = log₇(log x)

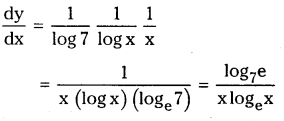
(xii) \(\frac{1}{a x^2+b x+c}\) (|a| + |b| + |c| ≠ 0)
Answer:

(xiii) e^2x log (3x + 4) (x > – 4/3)
Answer:
y = e^2x log (3x + 4) (x > – 4/3)

(xiv) (4 + x²) e^2x
Answer:
y = (4 + x²) e^2x
∴ \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = (4 + x²) \(\frac{\mathrm{d}}{\mathrm{dx}}\) (e^2x) + e^2x . \(\frac{\mathrm{d}}{\mathrm{dx}}\) (4 + x²)
= (4 + x²) (2e^2x) + e^2x (2x)
= 2e^2x (x² + x + 4)

(xv) \(\frac{a x+b}{c x+d}\) (|c| + |d| ≠ 0) (May 2022)
Answer:
y = \(\frac{a x+b}{c x+d}\)

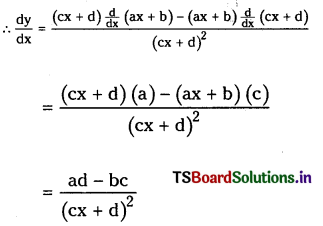
(xvi) a^x.e^x2 (Board New Model Paper)
Answer:
y = a^x.e^x2
Then
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = a^x . \(\frac{\mathrm{d}}{\mathrm{dx}}\) (e^x2) + \(\frac{\mathrm{d}}{\mathrm{dx}}\) (a^x)
= a^x (2x) e^x2 + e^x2 . a^x log_ea
= a^x e^x2 (2x + log_e^a)
= y (2x + log_e^a)

Question 2.
If f(x) = (1 + x + x² + …… + x¹⁰⁰) then find f ‘(1). (V.S.A.Q.)
Answer:
f(x) = (1 + x + x² + ……. + x¹⁰⁰)
Then f(x) = 1 + 2x+ 3x² + …………….. + 100x⁹⁹
and f’(1) = 1 + 2 + 3 + ………………. + 100
= \(\frac{100(100+1)}{2}\) = 101 × 50 = 5050
(∵ Σn = \(\frac{\mathrm{n}(\mathrm{n}+1)}{2}\))

Question 3.
If f(x) = 2x + 3x – 5 then prove that f ‘(0) + 3f ‘( -1) = 0. (V.S.A.Q.)
Answer:
Given f(x) = 2x² + 3x – 5
Then f'(x) = 4x + 3
∴ f(0) + 3f (- 1) = 3 + 3 [4 (- 1) + 3] = 3 – 3 = 0

II.
Question 1.
Find the derivatives of the following functions from the first principle. (S.A.Q.)
(i) x³
Answer:
Let f(x) = x³ then

(ii) x⁴ + 4
Answer:
let f(x) = x⁴ + 4

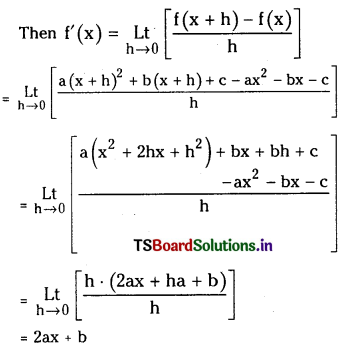
(iii) ax² + bx + c
Answer:
Let f(x) = ax² + bx + c

(iv) √x + 1
Answer:
Let f(x) = √x + 1

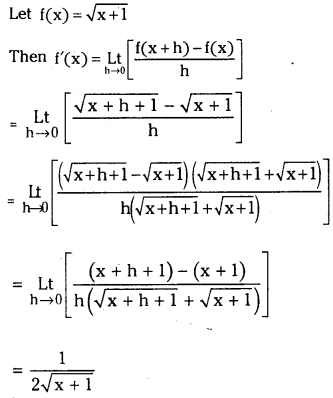
(v) sin 2x (Board New Model Paper)
Answer:
Let f(x) = sin 2x

(vi) cos ax (May 2014, March 2013, 2011)
Answer:
Let f(x) = cos ax

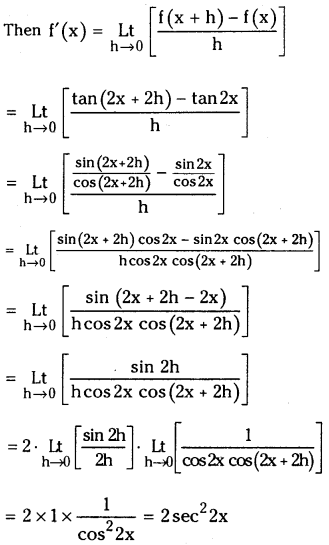
(vii) tan 2x (March 2014, May 2011)
Answer:
Let f(x) = tan 2x

(viii) cot x
Answer:
let f(x) = cot x
then

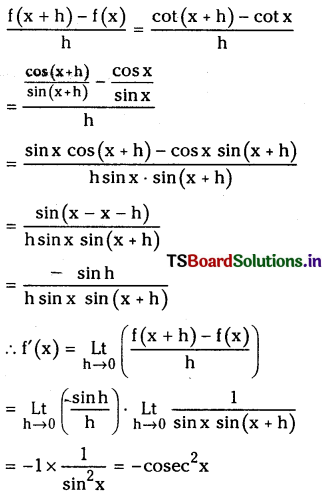
(ix) sec 3x
Answer:
Let f(x) = sec 3x
then

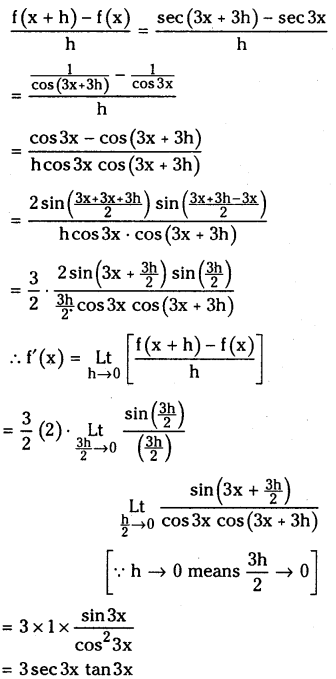
(x) x sin x
Answer:
Let f(x) = x sin x
Then f(x + h) – f(x) = (x + h) sin (x + h) – x sin x
= x [sin(x + h) – sin x] + h sin (x + h)

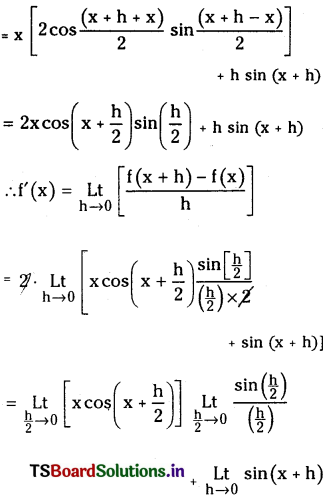
= x cos x × 1 + sin x
= x cos x + sin x

(xi) cos²x
Answer:
Let f(x) = cos²x
Then f (x + h) – f(x) = cos² (x + h) – cos²x
= [1 – sin²(x + h)] – (1 – sin²x)
= sin²x – sin²(x + h)
= sin (x + x + h) sin (x – x – h)
= sin (2x + h) sin (- h)

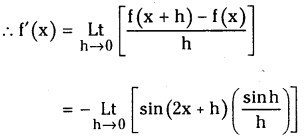
= – sin 2x × 1 = – sin 2x

Question 2.
Find the derivatives of the following functions. (S.A.Q.)
(i) \(\frac{1-x \sqrt{x}}{1+x \sqrt{x}}\) (x > 0)
Answer:

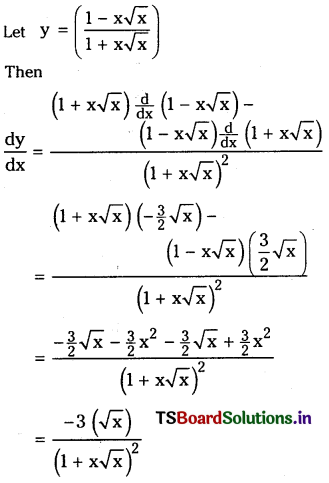
(ii) xⁿ n^x log (nx), (x > 0, n ∈ N)
Answer:
Let y = xⁿ n^x log (nx)
Then

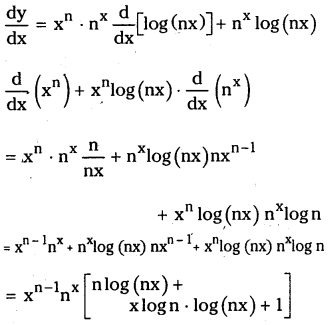
(iii) ax²ⁿ log x + bxⁿ e^-x
Answer:
Let y = ax²ⁿ log x + bxⁿ e^-x

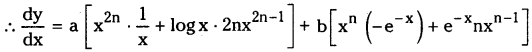
= a [x^{2n – 1} + 2nx^{2n – 1} log x] + b [- xⁿ e^-x + ne^-x x^{n – 1}]
= ax^{2n – 1} + 2anx^{2n – 1} log x – bxⁿe^-x + bne^-x x^{n – 1}

(iv) \(\left(\frac{1}{x}-x\right)^3\) e^x
Answer:

Question 3.
Show that the function f(x) = | x | + | x – 1| x ∈ R is differentiable for all real numbers except for 0 and 1. (S.A.Q.)
Answer:
f(x) = |x| + |x – 1| ∀ x ∈ R
then f(x) = x + x – 1 = 2x – 1, x ≥ 1
= x – (x – 1) = x – x + 1 = 1, 0 < x < 1
= – x – (x – 1)
= – x – x + 1 = 1 – 2x; x ≤ 0
∴ f(x) = 2x – 1, x ≥ 1
= 1, 0 < x < 1 = 1 – 2x; x ≤ 0 If x > 1, then f(x) = 2x – 1 which is a polynomial differentiable for all x > 1.
If 0 < x ≤ 1, then f(x) = 1 = Constant which is differentiable.

Case (i): Differentiability at x = 0:

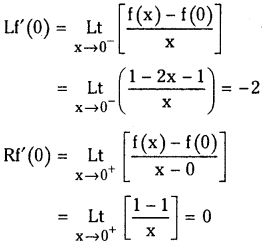
∵ Lf'(0) ≠ Rf'(0), the function f is not differentiable at x = 0.

Case (i): Differentiability at x = 1:

∵ Lf'(1) ≠ Rf'(1) we say that f(x) is not differentiable at x = 1.
∴ f(x) is differentiable for all real x except zero and one.

Question 4.
Verify whether the following function is differentiable at 1 and 3. (S.A.Q.)

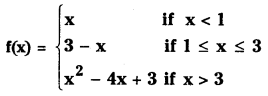
Answer:
Case (i):

Case (ii):

Since Lf'(3) ≠ Rf'(3), f(x) is not differentiable at x = 3.

Question 5.
Is the following function f differentiable at 2 ? Justify. (S.A.Q.)

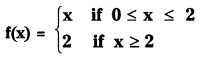
Answer:

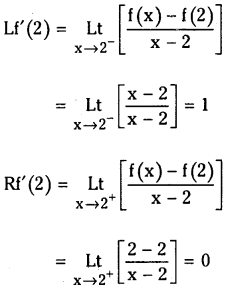
Since Lf'(2) ≠ Rf'(2), we say f(x) is not differentiable at x = 2.