TS Inter 1st Year Maths 1A Solutions Chapter 3 Matrices Ex 3(h)

Students must practice these TS Intermediate Maths 1A Solutions Chapter 3 Matrices Ex 3(h) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1A Matrices Solutions Exercise 3(h)

Question 1.
Solve the following systems of equations.
(i) By using Cramer’s rule and Matrix inversion method, when the coefficient matrix is non-singular.
(ii) By using Gauss Jordan Method. Also deter-mine whether the system has a unique solution or infinite number of solutions or no solution and find the solutions if exist.
I) 5x – 6y + 4z = 15
7x + 4y-3z = 17
2x + y + 6z = 46
Answer:
i) Cramer’s rule
Δ = \(\left|\begin{array}{rrr}
5 & -6 & 4 \\
7 & 4 & -3 \\
2 & 1 & 6
\end{array}\right|\)
= 5(24 + 3) + 6(42 + 6) + 4(7 – 8)
= 135 + 288-4 = 419 ≠ 0
Hence Cramer’s rule is applicable.

Δ₁ = \(\left|\begin{array}{rrr}
15 & -6 & 4 \\
19 & 4 & -3 \\
46 & 1 & 6
\end{array}\right|\)
= 15(24 + 3) + 6(114 + 138) + 4(19 -184)
= 405 + 1512 – 660
= 1917 – 660
= 1257

Δ₂ = \(\left|\begin{array}{rrr}
5 & 15 & 4 \\
7 & 19 & -3 \\
2 & 46 & 6
\end{array}\right|\)
= = 5(114 + 138) -15(42 + 6) + 4(322 – 38)
= 1260 – 720 + 1136
= 1676

Δ₃ = \(\left|\begin{array}{rrr}
5 & -6 & 15 \\
7 & 4 & 19 \\
2 & 1 & 46
\end{array}\right|\)
= 5(184 – 19) + 6 (322 – 38) + 15 (7 – 8)
= 825 + 1704 – 15
= 2529 – 15
= 2514

∴ x = \(\frac{\Delta_1}{\Delta}=\frac{1257}{419}\) = 3
y = \(\frac{\Delta_2}{\Delta}=\frac{1676}{419}\) = 4
z = \(\frac{\Delta_3}{\Delta}=\frac{2514}{419}\) = 6
∴ Solution is x = 3, y = 4, and z = 6

ii) Matrix Inversion method:
Use the formula A^-1 = \(\frac{{Adj} A}{{det} A}\)

iii) Gauss Jordan Method:
Augmented matrix of the system is

The given system is consistent and has a unique solution given by x = 3, y = 4, z = 6.

Question 2.
x + y + z = 1
2x + 2y + 3z = 6
x + 4y + 9z = 3
Answer:
i) Cramer’s rule :
Δ = \(\left|\begin{array}{lll}
1 & 1 & 1 \\
2 & 2 & 3 \\
1 & 4 & 9
\end{array}\right|\)
= 1(18 – 12) – 1(18 – 3) + 1(8 – 2)
= 6- 15 + 6
= -3

Δ₁ = \(\left|\begin{array}{lll}
1 & 1 & 1 \\
6 & 2 & 3 \\
3 & 4 & 9
\end{array}\right|\)
= 1(18 – 12) – 1(54 – 9) + 1(24 – 6)
= 6 – 45 + 18
= -21

Δ₂ = \(\left|\begin{array}{lll}
1 & 1 & 1 \\
2 & 6 & 3 \\
1 & 3 & 9
\end{array}\right|\)
= 1(54 – 9) – 1(18 – 3) + 1(6 – 6)
= 45 – 15
= 30

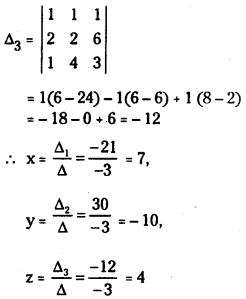
∴ Solution is x = 7, y = -10, and z = 4.

ii) Matrix Inversion Method:

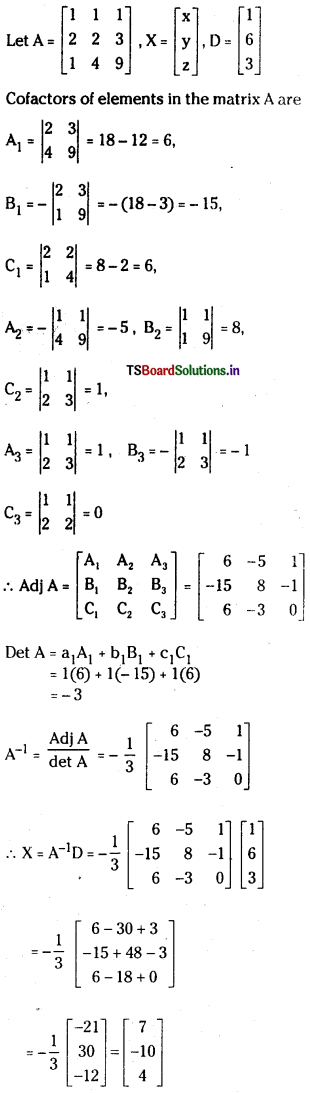
∴ Solution is x = 7, y = -10 and z = 4

iii) Gauss Jordan Method:
Augmented matrix of the system

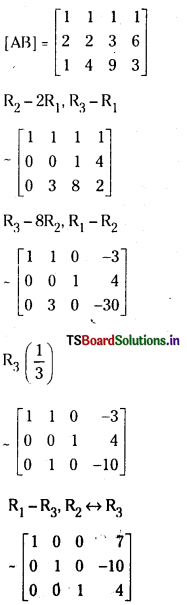
The given system is consistent and has a unique solution given by x = 7,y = -10,z = 4. [∵ ρ(A) = ρ(AB)]

Question 3.
x – y + 3z = 5 (March 2015-T.S)
4x + 2y – z = 0
-x + 3y + z = 5
Answer:
i) Cramer’s rule
Δ = \(\left|\begin{array}{rrr}
1 & -1 & 3 \\
4 & 2 & -1 \\
-1 & 3 & 1
\end{array}\right|\)
= 1(2 + 3) + 1(4-1) + 3(12 + 2)
= 5 + 3 + 42
= 50 ≠ 0
Cramer’s rule is applicable.

Δ₁ = \(\left|\begin{array}{rrr}
5 & -1 & 3 \\
0 & 2 & -1 \\
5 & 3 & 1
\end{array}\right|\)
= 5(2 + 3) + 1(0+ 5) + 3(0 -10)
= 25 + 5 – 30
= 0

Δ₂ = \(\left|\begin{array}{rrr}
1 & 5 & 3 \\
4 & 0 & -1 \\
-1 & 5 & 1
\end{array}\right|\)
= 1(0+ 5)-5(4-1)+ 3(20)
= 5 – 15 + 60 = 0

Δ₃ = \(\left|\begin{array}{rrr}
1 & -1 & 5 \\
4 & 2 & 0 \\
-1 & 3 & 5
\end{array}\right|\)
= 1(10 – 0) + 1(20 – 0)+ 5(12 + 2)
= 10 + 20 + 70
= 100

∴ x = \(\frac{\Delta_1}{\Delta}\) = 0
y = \(\frac{\Delta_2}{\Delta}=\frac{50}{50}\) = 1
z = \(\frac{\Delta_3}{\Delta}=\frac{100}{50}\) = 2
∴ x = 0, y = 1 and z = 2.

ii) Matrix Inversion Method:

iii) Gauss Jordan Method:

The given system of equations is consistent since ρ(A) = ρ(AB) = 3 and the system has a unique solution. x = 0, y = 1, z = 2.

Question 4.
2x + 6y + 11 = 0
6x + 20y – 6z + 3 = 0
6y – 18z + 1 = 0
Answer:
Δ = \(\left|\begin{array}{rrr}
2 & 6 & 0 \\
6 & 20 & -6 \\
0 & 6 & -18
\end{array}\right|\)
= 2(- 360 + 36) – 6(-108-0) + 0(36)
= -648 + 648 = 0
Cramer’s and matrix inversion methods are not applicable.

Gauss Jordan Process:
The augmented matrix of the given system is

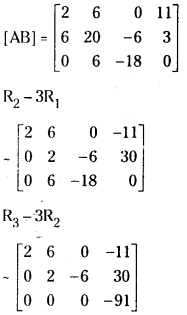
Since ρ(A) = 2 and ρ(AB) = 3, the given system is not consistent and has no solution.

Question 5.
2x – y + 3z = 9
x + y + z = 6
x – y + z = 2 (May 2014, Mar. ’14, ’05, ’02)
Answer:
i) Cramer’s rule :

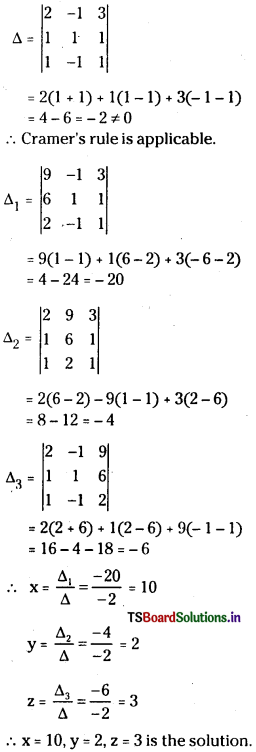
ii) Martix Inversion Method:

det A = 2(2) + 1(0) + 3(- 2)
= 4 -6 = -2 ≠ 0
∴ A^-1 exists and A^-1 = \(\frac{{Adj} \mathrm{A}}{{det} \mathrm{A}}\)

∴ x = 1, y = 2, z = 3 is the solution.

iii) Gauss Jordan Method:
Augmented matrix of the system

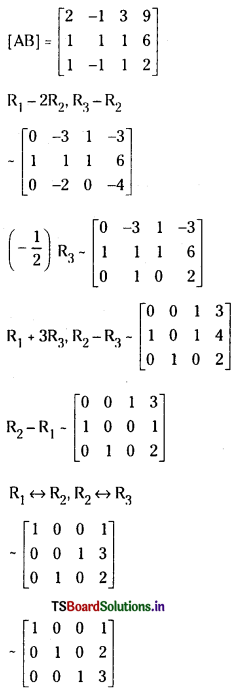
Since ρ(A) = ρ(AB) = 3; the system is consistent and has a unique solution given by x = 1, y = 2, z = 3.

Question 6.
2x- y + 8z = 13
3x + 4y + 5z = 18
5x – 2y + 7z = 20 (March 2004, 03, ’01) (Board New Model Paper)
Answer:
i) Cramer’s rule :

ii) Matrix Inversion Method:

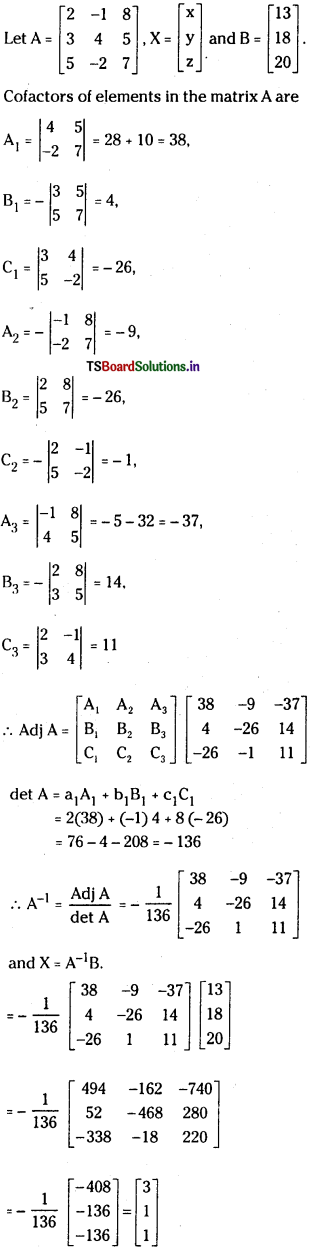
∴ Solution is x = 3, y = 1 and z = 1

iii) Gauss Jordan Method:
Augmented matrix of the system

Since ρ(A) = ρ(AB) = 3, the system is consistent and has a unique solution given by x = 3, y = 1 and z = 1.
Then the cofactors of elements in the matrix A are

Question 7.
2x – y + 3z = 8
-x + 2y + z = 4
3x + y – 4z = 0
Answer:
i) Cramer’s rule :
Δ = \(\left|\begin{array}{ccc}
2 & -1 & 3 \\
-1 & 2 & 1 \\
3 & 1 & -4
\end{array}\right|\)
= 2(- 8 – 1) + 1(4 – 3) + 3(- 1-6)
= -18 + 1 – 21 = -38 ≠ 0
Cramer’s rule is applicable.

Δ₁ = \(\left|\begin{array}{ccc}
8 & -1 & 3 \\
4 & 2 & 1 \\
0 & 1 & -4
\end{array}\right|\)
= 8(- 8 – 1) + 1(- 16 – 0) + 3(4 – 0)
= -72 – 16 + 12
= -76

Δ₂ = \(\left|\begin{array}{ccc}
2 & 8 & 3 \\
-1 & 4 & 1 \\
3 & 0 & -4
\end{array}\right|\)
= 2(- 16 – 0) – 8(4 – 3) + 3(0 – 12)
= – 32 – 8 – 36 = – 76

Δ₃ = \(\left|\begin{array}{ccc}
2 & -1 & 8 \\
-1 & 2 & 4 \\
3 & 1 & 0
\end{array}\right|\)
= 2(0 – 4) + 1(0 – 12) + 8(-1 – 6)
= -8 – 12 – 56
= -76
∴ x = \(\frac{\Delta_1}{\Delta}=\frac{-76}{-38}\) = 2
y = \(\frac{\Delta_2}{\Delta}=\frac{-76}{-38}\) = 2
z = \(\frac{\Delta_3}{\Delta}=\frac{-76}{-38}\) = 2
∴ Solution is x = 2, y =2, z = 2.

Matrix Inversion Method:

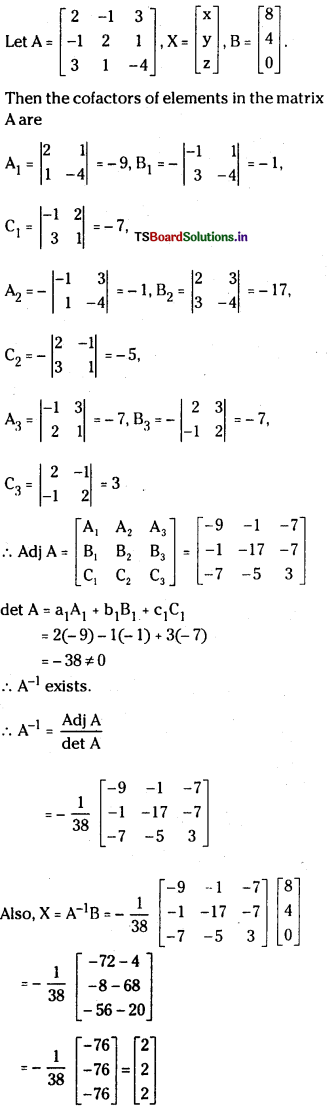
∴ Solution is x = 2, y = 2 and z = 2

iii) Gauss Jordan Method:
The augmented matrix of the system is

∴ ρ(A) = ρ(AB) = 3 ; the system is consistent and has a unique solution, x = 2, y = 2 and z = 2.

Question 8.
x + y + z = 9
2x + 5y + 7z = 52
2x + y-z = 0 (May 2011)
Answer:
i) Cramer’s rule :
Δ = \(\left|\begin{array}{ccc}
1 & 1 & 1 \\
2 & 5 & 7 \\
2 & 1 & -1
\end{array}\right|\)
= 1(-5 – 7) – 1(-2 – 14) + 1(2 – 10)
= – 12 + 16-8 = -4 ≠ 0
∴ The Cramer’s method is applicable.

Δ₁ = \(\left|\begin{array}{ccc}
9 & 1 & 1 \\
52 & 5 & 7 \\
0 & 1 & -1
\end{array}\right|\)
= 9(-5 – 7) -1(-52) + 1(52)
= -108 + 52 + 52 =-4

Δ₂ = \(\left|\begin{array}{ccc}
1 & 9 & 1 \\
2 & 52 & 7 \\
2 & 0 & -1
\end{array}\right|\)
= 1(- 52 – 0) – 9(- 2 – 14) + 1(0 – 104)
= -52 + 144 – 104
= -12

Δ₃ = \(\left|\begin{array}{ccc}
1 & 1 & 9 \\
2 & 5 & 52 \\
2 & 1 & 0
\end{array}\right|\)
= 1(0 – 52) -1(0 – 104) + 9(2 – 10)
= -52 + 104 – 72
= -20
∴ x = \(\frac{\Delta_1}{\Delta}=\frac{-4}{-4}\) = 1
y = \(\frac{\Delta_2}{\Delta}=\frac{-12}{-4}\) = 3
z = \(\frac{\Delta_3}{\Delta}=\frac{-20}{-4}\) = 5
x = 1, y = 3, z = 5 is a solution.

ii) Matrix Inversion Method:

∴ x = 1, y = 3, z = 5 is the solution.

iii) Gauss Jordan Method:
Augmented matrix

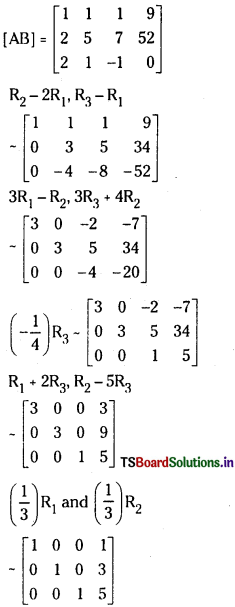
ρ(A) = ρ(AB) = 3 and the system is consistent.
The system has a unique solution given by
x = 1, y = 3 and z = 5.