TS Inter 1st Year Economics Study Material Chapter 10 అర్థశాస్త్రంలో ప్రాథమిక గణాంకశాస్త్ర భావనలు

Telangana TSBIE TS Inter 1st Year Economics Study Material 10th Lesson అర్థశాస్త్రంలో ప్రాథమిక గణాంకశాస్త్ర భావనలు Textbook Questions and Answers.

TS Inter 1st Year Economics Study Material 10th Lesson అర్థశాస్త్రంలో ప్రాథమిక గణాంకశాస్త్ర భావనలు

వ్యాసరూప సమాధాన ప్రశ్నలు:

ప్రశ్న 1.
ఏక పరిమాణ చిత్రపటాలను తగిన ఉదాహరణలతో వివరించండి.
జవాబు.
బార్ పొడవును మాత్రమే లెక్కలోకి తీసుకుంటారు, వెడల్పు లెక్కించరు. అందువల్ల వీటిని “ఏకపరిమాణ చిత్రం” అంటారు. ఈ ఏకపరిమాణ చిత్రాలు ముఖ్యంగా నాలుగు రకాలు.

1. సాధారణ బార్పటాలు
2. ఉప విభాజిత బార్పటాలు
3. బహుళ బారటాలు
4. శాతపు బార్పటాలు

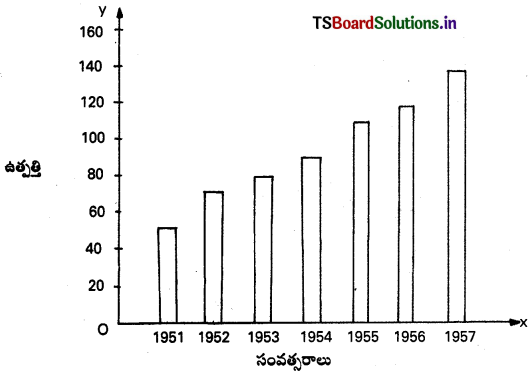
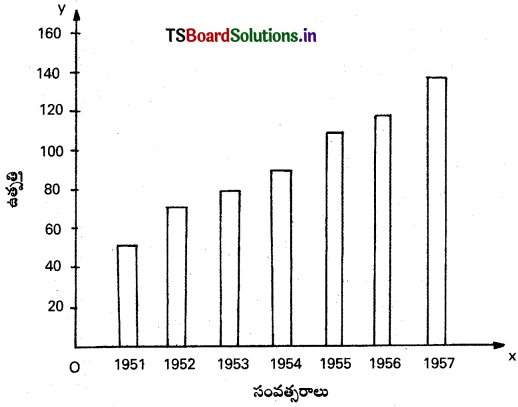
1. సాధారణ బార్పటం :
దీనిని ఒక చలనరాశిలో మార్పు చూపడానికి ఉపయోగిస్తారు.
ఉదా :

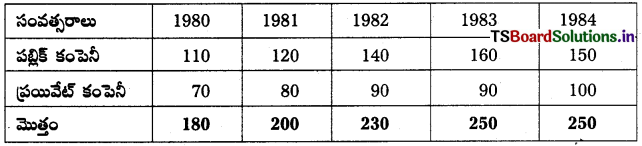
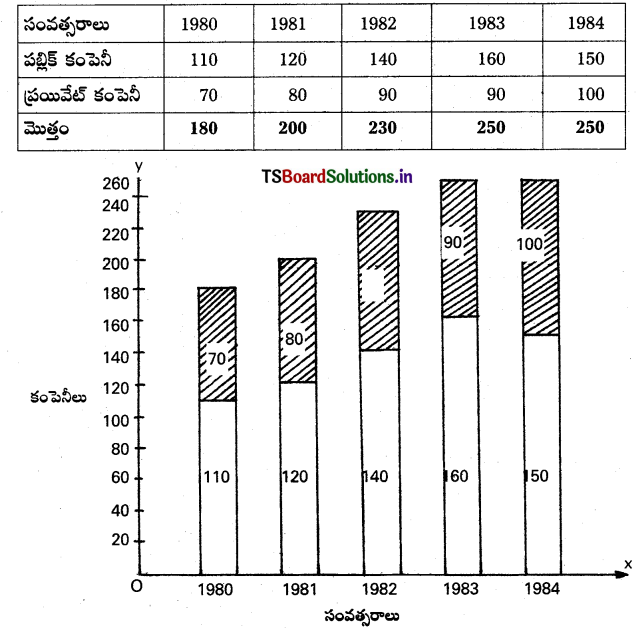
2. ఉపవిభాజిత బారటం :
దీనిలో మొత్తం దత్తాంశంలోని భాగాలు బార్ లో చూపించవచ్చు.
ఉదా :

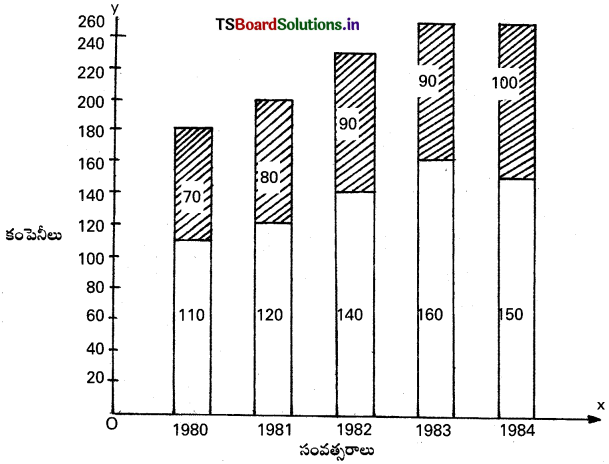
3. బహుళబార్ పటం :
అంతర సంబంధమున్న దత్తాంశం ఒకే పటంలో చూపడానికి బహుళబార్ ఉపయోగిస్తారు.
ఉదా :

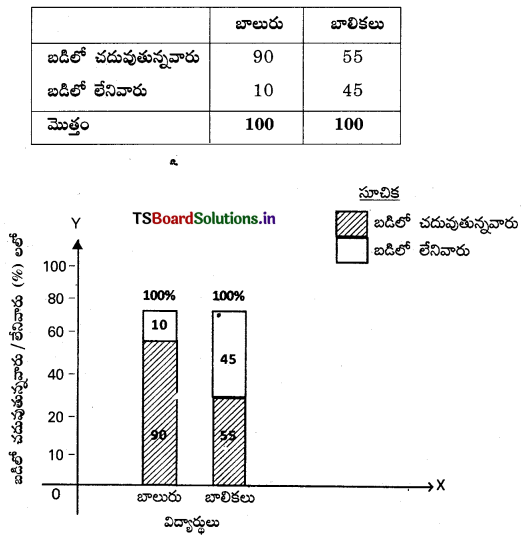
4. శాతపు బార్ పటం :
దత్తాంశంలోని మార్పులు సులభంగా గమనించడానికి శాతపు బార్ ఉపయోగిస్తారు. బార్ పొడవు నూరు యూనిట్లుగా విభాగం పొందుతుంది.
ఉదా :

ప్రశ్న 2.
ఈ క్రింది దత్తాంశానికి అంక మధ్యమం కనుగొనండి.

సాధన.
పై దత్తాంశం విలీన శ్రేణులకు చెందింది. దీని మినహాయింపు శ్రేణులలోనికి మార్చి వ్రాయగా అనగా తరగతిలో దిగువ అవధిలో 0.5 తీసివేయాలి, ఎగువ అవధికి 0.5 కలపాలి. అలా చేయటం ద్వారా విలీన శ్రేణులను మినహాయింపు శ్రేణులుగా మార్చవచ్చు. పై దత్తాంశాన్ని అలా మార్చి వ్రాయగా

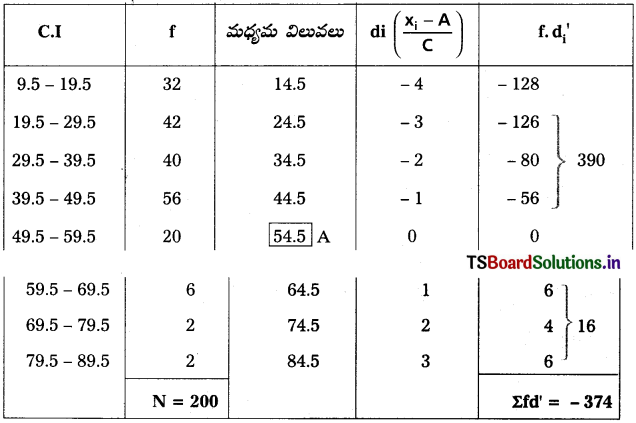
\(\overline{\mathrm{X}}=\mathrm{A}+\frac{\sum \mathrm{fd}^{\prime}}{\mathrm{N}} \times \mathrm{i}\)
ఇక్కడ A = ఊహించిన అంకమధ్యమం = 54.5
Σfd’ = – 37.4
N = పౌనఃపున్యాల మొత్తం = 200
i = తరగతి అంతరం = 10
విలువలను పై సూత్రంలో ప్రతిక్షేపించగా
\(\bar{x}=54.5+\left(\frac{-374}{200}\right) \times 10\)
= 54.5 + (- 1.87) × 10
= 54.5 + (- 18.7)
\(\bar{x}\) = 35.8.

ప్రశ్న 3.
దిగువ పేర్కొన్న దత్తాంశానికి మధ్యగతాన్ని కనుగొనండి.

సాధన.

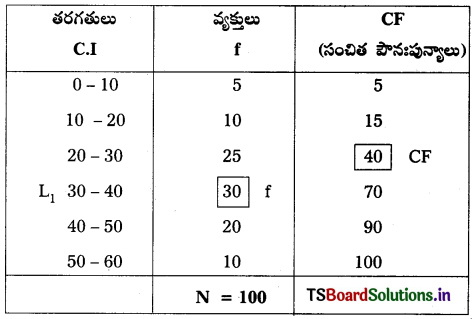
మధ్యగతం = L₁ + \(\left(\frac{\frac{\mathrm{N}}{2}-\mathrm{CF}}{\mathrm{f}}\right)\) × i
మధ్యగత స్థానం = \(\frac{N}{2}\) వ అంశం
= \(\frac{100}{2}\) వ అంశం = 50 వ అంశం
L₁ = మధ్యగత తరగతి దిగువ అవధి
\(\frac{N}{2}\) = మధ్యగత అంశం = 50
CF = మధ్యగతమైన తరగతికి ముందున్న తరగతి సంచిత పౌనఃపున్యం = 40
f = మధ్యగతమైన తరగతికి సాధారణ పౌనఃపున్యం = 30
i = తరగతి అంతరం = 10
విలువలను పై సూత్రంలో ప్రతిక్షేపించగా = 30 + \(\left(\frac{50-40}{30}\right)\) × 10
= 30 + \(\left(\frac{10}{30}\right)\) × 10
= 30 + (0.33) × 10
= 30 + 3.33 = 33.33
∴ మధ్యగతం = 33.3.

ప్రశ్న 4.
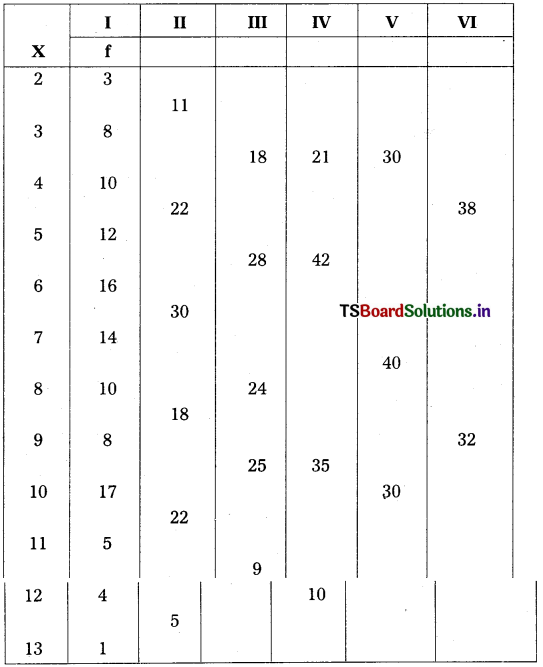
ఈ క్రింది దత్తాంశానికి బహుళకాన్ని కనుగొనండి.

సాధన.

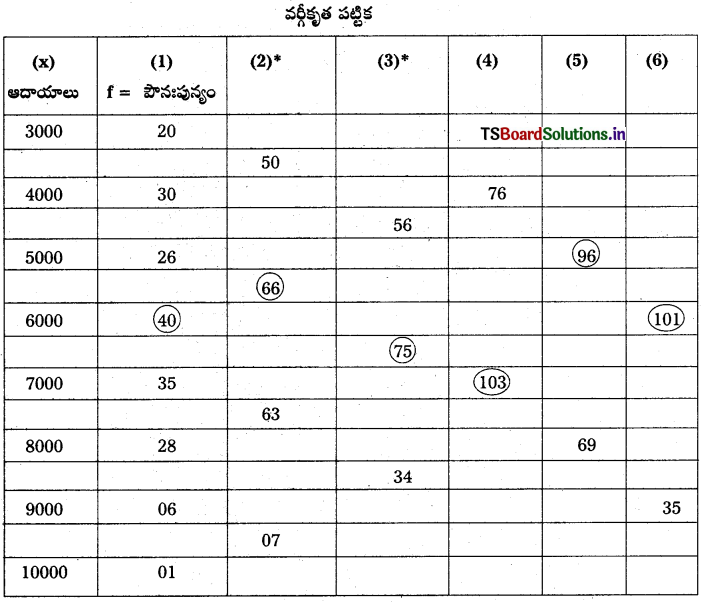
(2)* = ప్రతి రెండు అడ్డు వరుసలలో గల పౌనఃపున్యాల సంకలనం.
(3)* = మొదటి అడ్డు వరుసలో గల పౌనఃపున్యాన్ని వదిలి, ప్రతి రెండు అడ్డు వరుసల పౌనఃపున్యాల సంకలనం.
(4)* = ప్రతి మూడు అడ్డు వరుసలలో గల పౌనఃపున్యాల సంకలనం.
(5)* = మొదటి అడ్డు వరుసలో గల పౌనఃపున్యాన్ని వదలి ప్రతి మూడు అడ్డు వరుసలతో పౌనఃపున్యాల సంకలనం.
(6)* = మొదటి రెండు అడ్డు వరుసలను వదిలి ప్రతి మూడు పౌనఃపున్యాల సంకలనం.

ఈ కింద ఉన్న విశ్లేషణ పట్టికకు వర్గీకృత పట్టిక ఆధారంగా చేయటమైనది.

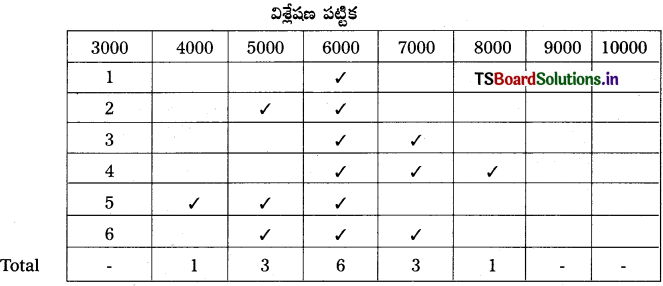
విశ్లేషణ పట్టికను పరిశీలించినప్పుడు 6000 అనే అంశం అధిక పర్యాయాలు అంటే 6 పర్యాయాలు వచ్చింది.
కాబట్టి బాహుళకం Z = 6000.

ప్రశ్న 5.
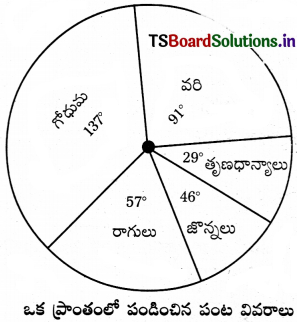
క్రింది దత్తాంశానికి ‘పై’ (Pie) చిత్రము గీయండి.

సాధన.

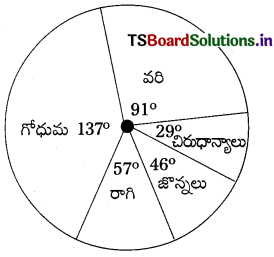
Area changed into Degree వరి = \(\frac{16 \times 360}{63}\) = 90°
గోధుమ = \(\frac{24 \times 360}{63}\) = 137°
రాగి = \(\frac{10 \times 360}{63}\) = 57°
జొన్నలు = \(\frac{8 \times 360}{63}\) = 46°
చిరుధాన్యాలు = \(\frac{5 \times 360}{63}\) = 29°
∴ మొత్తం = 360°.

స్వల్ప సమాధాన ప్రశ్నలు:

ప్రశ్న 1.
గణాంక శాస్త్రం అంటే ఏమిటి ? అర్థశాస్త్రంతో దానిక గల సంబంధాన్ని వివరించండి.
జవాబు.
గణాంక శాస్త్రానికి అనేక శాస్త్రాలతో సన్నిహిత సంబంధముంది. 19వ శతాబ్దం నుంచి గణాంక శాస్త్రం, అర్థశాస్త్రం చాలా సాన్నిహిత్యం పెంపొందించుకున్నాయి. అర్థశాస్త్ర విశ్లేషణ అధ్యయనంలో, సిద్ధాంత నిర్మాణంలో సాంప్రదాయ ఆర్థికవేత్తలు నిగమన పద్ధతిని ఉపయోగించేవారు.

అయితే కాలక్రమేణా ఆర్థిక విషయాల పరిశీలనకు, అర్థశాస్త్రాన్ని అర్థం చేసుకోవడానికి గణాంకశాస్త్ర పరిజ్ఞానం అవసరమని J.S.

మిల్, జీవాన్స్, కీన్స్ లాంటి ఆర్థికవేత్తలు పేర్కొన్నారు. అర్థశాస్త్ర సిద్ధాంతాలను యదార్థ జీవితానికి అన్వయించడానికి, న్యాయబద్ధతను నిర్ణయించడానికి ‘ఆగమన పద్ధతి’ ని ప్రవేశపెట్టడంతో గణాంక, అర్థశాస్త్రాలు సన్నిహితమవడం ప్రారంభమైంది. ‘జీవాన్స్’ సంఖ్యా దత్తాంశాన్ని ఉపయోగించి ‘కాలశ్రేణుల విశ్లేషణ’, సూచీ సంఖ్యల అధ్యయనం చేశారు.

1704లో గ్రెగొరికింగ్ వస్తు సప్లయ్కి, వస్తువు ధరకు ఉన్న సంబంధాన్ని గణాంకాల రూపంలో నిరూపించడానికి ప్రయత్నం చేశాడు. బౌలే, పియర్సన్, W.I. కింగ్, ఫిషర్ మొదలైన గణాంకవేత్తలు తమ సేవలతో గణాంకశాస్త్రాన్ని, అర్థ శాస్త్రానికి మరింత చేరువ చేశారు.

అర్థశాస్త్ర విశ్లేషణ అంతా గణాంక దత్తాంశంపై పూర్తిగా ఆధారపడి ఉంటుంది. పేదరికం, నిరుద్యోగం, ధరల పెరుగుదల మొదలైన ఆర్థిక సమస్యల స్వభావం, స్వరూపం, గణాంక వివరాలు లేకుండా తెలుసుకోవడం సాధ్యం కాదు. ఆర్థిక సమస్యలన్నీ గణాంక పద్ధతుల ద్వారా పరిశీలించడం జరుగుతుంది.

ఆర్థిక విశ్లేషణలో సాంఖ్యక వివరాలు, పద్ధతులు చాలా శక్తివంతమైన పరికరాలు, గణాంక శాస్త్రం అర్థశాస్త్రానికి ముఖ్యంగా ‘మూడు’ విధాలుగా ఉపయోగపడుతుంది.

1. ఆర్థిక సమస్యలను క్షుణ్ణంగా తెలుసుకోవడానికి.
2. ఆర్థిక సిద్ధాంతాలకు సాంఖ్యారూపమేర్పరచటం, ఆర్థిక సిద్ధాంతాల ఉపకల్పనలను (Hypothesis) పరీక్ష చేయడం.
3. ఆర్థిక సిద్ధాంతాల భవిష్యత్ అంచనాలను పరీక్షించడం.
   ఉదా : కీన్స్ ప్రతిపాదించిన వినియోగ ప్రవృత్తి సిద్ధాంతాన్ని కూజెనట్స్ దత్తాంశాన్ని సేకరించి సంఖ్యారూప మేర్పరిస్తే దాని ఆధారంగా వినియోగ ప్రవృత్తి సిద్ధాంతాన్ని మార్పుచేసి డ్యూసెన్బెర్రీ, ఫ్రీడ్మన్ కొత్త రీతులలో ప్రతిపాదించారు.

ప్రశ్న 2.
తగిన ఉదాహరణలతో సాధారణ, ఉప విభాజిత చిత్రపటాలను వివరించండి.
జవాబు.
1. సాధారణ (సామాన్య) బార్పటం : దీనిని ఒక చలనరాశిలో మార్పు చూపడానికి ఉపయోగిస్తారు.
ఉదా :

2. ఉపవిభాజిత బార్పటం : దీనిలో మొత్తం దత్తాంశంలోని భాగాలు బార్ లో చూపించవచ్చు.
ఉదా :

ప్రశ్న 3.
క్రింది దత్తాంశానికి అంక మధ్యమాన్ని కనుగొనండి.

జవాబు.

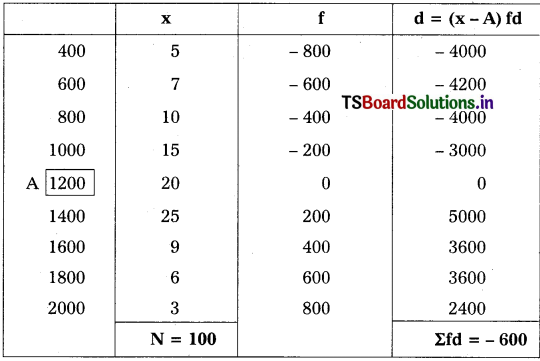
\(\overline{\mathrm{X}}=\mathrm{A}+\frac{\Sigma \mathrm{fd}}{\mathrm{N}}\)
ఇక్కడ \(\overline{\mathrm{X}}\) = అంక మధ్యమం
A = ఊహించిన అంక మధ్యమం = 1200
Σfd = ఊహించిన అంక మధ్యమం నుంచి తీసుకొన్న విచలనాలను (d) వాటి అనురూప పౌనఃపున్యాలతో (f) తో గుణించగా వచ్చిన లబ్దాల సంకలనం = 600
N = పౌనఃపున్యాల మొత్తం = 100
విలువలను పై సూత్రంలో ప్రతిక్షేపించగా
= 1200 + \(\frac{(-600)}{100}\)
= 1200 + (- 6) = 1194
∴ \(\overline{\mathrm{X}}\) = 1194.

ప్రశ్న 4.
క్రింది దత్తాంశానికి మధ్యగతాన్ని కనుగొనండి.

జవాబు.

x	f	cf (సంచిత పౌనఃపున్యం)
10	5	5
20	8	13
30	12	25
40	20	45
50	30	75
60	16	91
70	10	101
80	7	108
90	8	116
	N = 116

 

మధ్యగత స్థానం = \(\frac{\mathrm{N}+1}{2}\)వ అంశం
ఇక్కడ N = పౌనఃపున్యాల మొత్తం = 116 = \(\frac{116+1}{2}\)వ అంశం
= \(\frac{117}{2}\) = 58.5
58.5 అంశం సంచిత పౌనఃపున్యం 75 లో ఉంది. అందువల్ల దాని అనురూప ‘x’ విలువ 50 మధ్యగతం అవుతుంది.
మధ్యగతం = 50.

ప్రశ్న 5.
ఈ క్రింది దత్తాంశానికి బహుళకము లెక్కించండి.

సాధన.

∴ Z = 16.

ప్రశ్న 6.
అంక మధ్యమం అంటే ఏమిటి ? దాని ప్రయోజనాలు, పరిమితులు తెల్పండి.
జవాబు.
అంక మధ్యమం అంటే అంశాల మొత్తం విలువలను, మొత్తం అంశాల సంఖ్యచే భాగించగా వచ్చేదే అంక మధ్యమం. ప్రయోజనాలు :

1. అంక మధ్యమాన్ని గణించడం అర్థం చేసుకోవడం చాలా సులభం.
2. దీని గణనలో ప్రతి అంశం పరిగణింపబడుటవలన ప్రతి అంశంచే ఇది ప్రభావితమౌతుంది.
3. దీని గణితాత్మక సమీకరణం దృఢంగా ఉండడంచేత ఏ పద్ధతులలో అంక మధ్యమాన్ని గణన చేసినప్పటికి ఒకే రకమైన సమాధానాన్ని పొందగలం.
4. తదుపరి బీజీయ గణనకు ఇది ఉపకరించును.
5. వివిధ అంశాలను పోల్చుటలో దీనిని విరివిగా ఉపయోగిస్తారు.

పరిమితులు :

1. గ్రాఫ్లో దీని విలువను గుర్తించలేం.
2. ఒక అంశంలో వచ్చిన ఒక చిన్న మార్పు ఫలితాలలో పెద్ద మార్పును తెస్తుంది. ఉదా : 3, 6, 9ల అంక మధ్యమం విలువ 6. కాని దీనికి 82 అనే అంశాన్ని చేర్చినపుడు అంక మధ్యమం 3 + 6 + 9 + 82 / 4 = 100/4 = 25. మొదటి మూడు అంశాల విలువతో పోల్చినపుడు నాల్గవ అంశం చేరికవల్ల విలువలో ఎక్కువ మార్పు ఏర్పడుటను గమనించవచ్చు.
3. అంకమధ్యమం, శ్రేణులలో గల చిన్న అంశాలకన్న పెద్ద అంశాలకు అధిక ప్రాధాన్యతను ఇస్తుంది.
4. ఇది మధ్యగతం మరియు బాహుళకం వలే తనిఖీ లేదా పరిశీలన ద్వారా గుర్తించబడదు.
5. ఇది కొన్ని సందర్భాలలో అసంబద్ధమైన ఫలితాలను ఇస్తుంది. ఉదా : ఒక కుటుంబంలో సభ్యుల సగటు ఎంత అన్నపుడు లెక్కించిన అంక మధ్యమం విలువ 4.3 అయితే ఆ విలువ అసంబద్ధంగా ఉంటుంది. ఎందుకంటే కుటుంబ సభ్యుల సంఖ్య భిన్నాలలో ఉండదు.

ప్రశ్న 7.
మధ్యగతం అంటే ఏమిటి ? దాని ప్రయోజనాలు, పరిమితులు తెల్పండి.
జవాబు.
ఒక విభాజనాన్ని ఏ విలువైతే రెండు సమభాగాలుగా విభజిస్తుందో, అంటే ఏ విలువకు అటు, ఇటు విభాగాన్ని పొందిన అంశాల సంఖ్య సమానంగా ఉంటుందో ఆ విలువను ‘మధ్యగతం’ అంటారు. దీనినే ‘స్థాన మాన సగటు’ (Positional averge) అని కూడా అంటారు.

మధ్యగతాన్ని లెక్కించడానికి దిగువ పేర్కొన్న పద్ధతిని ఉపయోగిస్తారు.

1. 1) ఇచ్చిన దత్తాంశాన్ని ఆరోహణ లేదా ఆవరోహణ క్రమంలో రాసుకోవాలి.
2. 2) వరుస క్రమంలో మధ్యస్థ విలువ లేదా సంఖ్యే మధ్యగతం, ఇవ్వబడిన అంశాల సంఖ్య N బేసి (odd) లేదా సంఖ్య అయినట్లయితే, \(\left(\frac{\mathrm{n}+1}{2}\right)^{\text {th }}\) వ అంశం మధ్యగతం అవుతుంది.
   ఇలాంటి స్థితిలో మధ్యగతం ఒకే ఒక విలువను కలిగి ఉంటుంది. ఇందుకు భిన్నంగా, అంశాల సంఖ్య సరి (even) సంఖ్య అయితే, వరుస క్రమంలో ఉన్న రెండు సంఖ్యల మధ్యస్థ విలువను మధ్యగతం విలువగా పరిగణిస్తారు. కాబట్టి ఈ పరిస్థితిలో మధ్యగతం లెక్కించడానికి \(\left(\frac{\mathrm{n}}{2}\right)^{\text {th }},\left(\frac{\mathrm{n}}{2}+1\right)^{\mathrm{th}}\)వ అంశాలను పరిగణించాలి.

ప్రయోజనాలు :

1. మధ్యగతం దృఢంగా నిర్వచింపబడుతుంది.
2. ఒక శ్రేణిలో గల అంశాలలో ఒక అంశం విలువ ఇతర అంశాల విలువలకు భిన్నంగా అత్యధికంగా ఉన్నప్పటికినీ మధ్యగతం విపరీత అంశాల విలువలచే ప్రభావం కాదు.
3. మధ్యగతాన్ని రేఖాచిత్రం ద్వారా కూడా గణన చేయడానికి వీలు కలుగుతుంది.
4. మధ్యగతాన్ని అర్థం చేసుకోవడం, గణించడం చాలా సులభం

పరిమితులు :

1. మధ్యగతం – స్థానపు సగటు కాబట్టి, దాని గణన శ్రేణిలోని ప్రతి అంశం యొక్క విలువపైన ఆధారపడి ఉండదు. కాబట్టి మధ్యగతం విలువ శ్రేణిలో గల అంశాలకు ప్రాతినిధ్యం వహిస్తుందని చెప్పలేం.
2. మధ్యగతం తదుపరి బీజగణిత విశ్లేషణకు ఉపయోగపడదు.
3. అవిచ్ఛిన్న శ్రేణులలో దీనిని అంతర్వేశనం (Interpolated) చేయాల్సి ఉంటుంది.
4. సరిసంఖ్య గల అంశాలు శ్రేణిలో ఉన్నప్పుడు, రెండు మధ్య విలువల అంక మధ్యమమే మధ్యగతం అవుతుంది.

ప్రశ్న 8.
బహుళకం అంటే ఏమిటి ? దాని ప్రయోజనాలు, లోపాలేవి ?
జవాబు.
ఒక విభాజనంలో ఒక అంశం విలువ తరచూ ఎక్కువ పర్యాయాలు కనిపించడాన్ని బహుళకం తెలుపుతుంది. శ్రేణులలో ఉన్న అంశాలలో ఏ విలువ అతి తరచుగా వస్తుందో ఆ విలువను, ఇంకా ఏ విలువ చుట్టూ అత్యధికంగా ఇతర విలువల పంపిణీ జరుగుతుందో ఆ విలువను ‘బహుళకంగా’ నిర్వచించవచ్చు.

ప్రయోజనాలు :

1. బహుళకం శ్రేణులలో అధిక పర్యాయాలు కనిపించే విలువ. మధ్యగతం మాదిరి దీని విలువ విడిగా (isalated) ఉండదు, శ్రేణిలోలేని అంశాల విలువను తెలిపే అంకమధ్యమంలాగా ఉండదు.
2. విపరీత అంశాల ప్రభావం దీనిపై ఉండదు. అందువల్ల ఇది శ్రేణిలోని అంశాలకు ప్రాతినిధ్యం వహించును.
3. రేఖా చిత్రం ద్వారా కూడా బహుళకాన్ని లెక్కించవచ్చు.
4. విస్తృత అవధులు ఉన్న తరగతులలో కూడా బహుళకాన్ని లెక్కించవచ్చు.
5. దత్తాంశంలోని గుణాత్మక విలువలను వర్గీకరించవలసినపుడు ఈ పద్ధతి ఉపయుక్తంగా ఉంటుంది.
6. బహుళకాన్ని అర్థం చేసుకోవడం, గణించడం సులభం.
7. ఇది నిత్య జీవితంలో తరచుగా ఉపయోగించే సగటు. ఉదాహరణకు తరగతి మార్కుల సగటు, ఒక విభాగంలో విద్యార్థుల సంఖ్యను కనుగొనుట మొదలైనవి.

లోపాలు :

1. ద్విబహుళకం, బహుళ బహుళకం శ్రేణులలో బహుళకాన్ని లెక్కించడం చాలా కష్టం.
2. కేంద్రీకృత విలువలపై మాత్రమే బహుళకం ఆధారపడుతుంది. బహుళకం విలువ కంటే అధిక విలువలు కలిగిన ఇతర అంశాలు ఉన్నా అవి పరిగణింపబడవు. అవిచ్ఛిన్న శ్రేణులలో కేవలం తరగతి అంతరాల అవధులు మాత్రమే పరిగణింపబడతాయి.
3. బహుళకం ప్రతిచయన మార్పులకు ఎక్కువగా గురవుతుంది.
4. బహుళకాన్ని వివిధ పద్ధతులలో లెక్కించినపుడు అంకమధ్యమం వలె ఒకే విలువ రాదు. గణనకు అనేక సూత్రాలు ఉన్నాయి. ఏది ఉపయోగించాలి అని సందేహం తలెత్తుతుంది.
5. ఇది బీజీయ ప్రస్తావనకు పనికి రాదు. అంకమధ్యమం వలె ఉమ్మడి బహుళక గణన సాధ్యం కాదు.
6. శ్రేణిలోని అంశాల సంఖ్య అత్యధికంగా ఉన్నప్పుడే బహుళకం ఆ శ్రేణిలోని విలువలకు ప్రాతినిధ్యం వహిస్తుంది.

ప్రశ్న 9.
ఆదర్శ లేదా మంచి సగటుకు ఉండవలసిన లక్షణాలను తెల్పండి ?
జవాబు.
ఆదర్శ లేదా మంచి సగటుకు ఉండవలసిన లక్షణాలు :

1. మంచి సగటు నిర్దిష్టంగా నిర్వచింపబడి ఉండాలి అంటే ఎవ్వరు తెలిపినా ఒకే అర్థం కలిగి ఉండాలి.
2. దత్తాంశంలోని మొత్తం అంశాలకు ప్రాతినిధ్యం వహించాలి.
3. బీజగణిత విశ్లేషణకు అనువుగా ఉండాలి.
4. దత్తాంశంలోని ఒకే ఒక అంశం లేదా కొన్ని అంశాలవల్ల ప్రభావితం కాకూడదు. అధిక విలువలు కలిగిన అంశాలు సగటును ప్రభావితం చేస్తే, ఆ సగటు శ్రేణిలో గల అన్ని అంశాలకు ప్రాతినిధ్యం వహించదు.
5.  మంచి సగటు లెక్కించడానికి సులభంగా ఉండి, సామాన్య మానవునికి కూడా సులభంగా అర్థమయ్యేట్లు ఉండాలి. దాని గణనకు క్లిష్టమైన గణిత ప్రక్రియలు అధిక మొత్తంలో ఉంటే అది సులభంగా అర్థం కాదు. అందువల్ల దాని ఉపయోగిత పరిమితంగా ఉంటుంది.
6. ప్రతిచయన స్థిరత్వం కలిగి ఉండాలి. అంటే ప్రతిచయన మార్పులకు సగటు ప్రభావితం కాకూడదు. ఒకే జనాభా నుంచి తీసుకున్న వేరు వేరు ప్రతి చయనాల సగటులలో పెద్దగా తేడా లేకుండా పరస్పరం దగ్గరగా ఉండాలి.

అతిస్వల్ప సమాధాన ప్రశ్నలు:

ప్రశ్న 1.
అర్థశాస్త్ర అధ్యయనంలో గణాంక శాస్త్ర ప్రాధాన్యతను తెలపండి ?
జవాబు.
ఆర్థిక విశ్లేషణలో గణాంక వివరాలు, గణాంక పద్ధతులు చాలా శక్తివంతమైన పరికరాలు. గణాంకశాస్త్రం, అర్థశాస్త్రానికి ముఖ్యంగా మూడు రకాలుగా ఉపయోగపడుతుంది.

• ఆర్థిక సమస్యలను క్షుణ్ణంగా తెలుసుకోవడానికి.
• సిద్ధాందంతాలకు సంఖ్యా రూపం ఏర్పరచడం.
• ఆర్థిక సిద్ధాంతాలకు పరికల్పనలను పరీక్ష చేయడం.
• ఆర్థిక సిద్ధాంతాల భవిష్యత్ అంచనాలు పరీక్షించడం.

ప్రశ్న 2.
చిత్రపటాల ఉపయోగాలు ఏమిటి ?
జవాబు.
గణాంక ఫలితాలను నమ్మకంగా, ఆకర్షణీయంగా సమర్పించడానికి చిత్రపటాలు ఉపయోగపడతాయి. చిత్రపటాలను సక్రమంగా నిర్మించినట్లయితే అవి దత్తాంశ ఫలితాలను స్పష్టంగా చూపిస్తాయి. చిత్రపటాల ఉపయోగాలను క్రింది విధంగా వివరించవచ్చు.

1. ఆకర్షణీయంగా, ఆసక్తిదాయకంగా ఉంటాయి.
2. ప్రత్యేక గణితశాస్త్ర పరిజ్ఞానం అవసరం లేదు.
3. దత్తాంశ సమర్పణ తేలిక.
4. పోల్చడం తేలిక.
5. జ్ఞాపకశక్తిని పెంపొందిస్తాయి.

ప్రశ్న 3.
“పై” (Pie) చిత్రం అంటే ఏమిటి ?
జవాబు.
‘పై’ చిత్రాన్ని వృత్తాలు అంటారు. దత్తాంశంలోని వివిధ అంశాలను లేదా భాగాలను చూపడానికి మరియు సరిపోల్చడానికి ఉపయోగించే వలయాలను వృత్తాలు అంటారు. ఇది ద్విపరిమాణ చిత్ర పటంలోనిది.

ప్రశ్న 4.
ఉప విభాజిత పటాల ఉపయోగాలు ఏమిటి ?
జవాబు.
దత్తాంశంలోని వివిధ భాగాలను ఒకే బార్లో చూపించడానికి ఈ విధమైన బార్ పటాలను గీస్తారు. ఈ పటాన్ని ‘అంశాల బార్ పటం’ (component bar diagram) అని కూడా అంటారు. ఈ పటాలు దత్తాంశపు మొత్తం వివరాలను వివిధ భాగాలుగా విభజించి గీయబడతాయి. వివిధ భాగాలను వేరుగా చూపడానికి వివిధ రంగులను ఉపయోగిస్తారు.

ప్రశ్న 5.
క్రింది విలువలకు మధ్యగతం కనుగొనండి 5, 7, 7, 8, 9, 10, 12, 15, 21
సాధన.
ఇచ్చిన దత్తాంశాన్ని ఆరోహణ క్రమంలో వ్రాయగా

క్రమసంఖ్య	x
1	5
2	7
3	7
4	8
5	9
6	10
7	12
8	15
9	21

మధ్యగతం = \(\frac{\mathrm{N}+1}{2}\)వ అంశం
ఇక్కడ N = అంశాల సంఖ్య = 9
మధ్యగతం = \(\frac{9+1}{2}\)వ అంశం
= \(\frac{10}{2}\)వ అంశం = 5వ అంశం
5వ అంశానికి అనురూపంగా ఉన్న విలువ = 9
∴ మధ్యగతం = 9

ప్రశ్న 6.
బహుళకం భావన గురించి తెలపండి.
జవాబు.
ఆంగ్లభాషలో బహుళకాన్ని Mode అంటారు. మోడ్ అనే మాట ల-మోడ్ అనే ప్ర గ్రహించబడింది. దీని అర్థం ఫ్యాషన్ బీజక్. బహుళకాన్ని శ్రేణులలో ఉన్న అంశాలలో ఏ విలువ అతి తరచుగా వస్తుందో ఆ విలువ ఇంకా ఏ విలువ చుట్టూ అత్యధికంగా ఇతర విలువల పంపిణీ జరుగుతుందో ఆ విలువలను ‘బహుళకం’ అంటారు.

ప్రశ్న 7.
హరమధ్యమం యొక్క ఉపయోగాలు తెలపండి.
జవాబు.
కాలం, దూరం, రేట్లు మొదలైన సమస్యలకు పరిష్కారానికి హరమాధ్యమాన్ని ఉపయోగిస్తారు.

ప్రశ్న 8.
గుణమధ్యమం భావన గురించి తెలపండి.
జవాబు.
గుణ మధ్యమం ఒక ప్రత్యేక రకమైన సగటు. శ్రేణిలో రెండు అంశాలు ఇచ్చినట్లయితే రెండు అంశాల లబ్దానికి వర్గమూలం (Square root) మూడు అంశాలు ఇచ్చినట్లయితే మూడు అంశాల లబ్దానికి ఘనమూలం (Cube root) ‘n’ అంశాలు ఇచ్చినట్లయితే Nవ మూలాన్ని (A/ ) లెక్కిస్తాం. “శ్రేణులలోని N అంశాల లబ్దానికి Nవ మూలాన్ని గుణమధ్యమం” అంటారు.
ఉదా : 2, 8ల గుణమధ్యమం రెండు అంశాల లబ్దానికి వర్గమూలం అంటే √2.8 = 4
ఉదా : 2, 3, 6ల గుణమధ్యమం మూడు అంశాల లబ్దానికి ఘనమూలం, అంటే = \(\sqrt[3]{2.3 .6}\)
లేదా (2.3.6)^1/3 = 3.3.
G.M. = \(\sqrt[n]{X_1, X_2, X_3 \ldots \ldots X_n}\)
G.M. = గుణ మధ్యమం
n = అంశాల సంఖ్య
X = అంశాల విలువలు.

ప్రశ్న 9.
మధ్యగతం యొక్క ప్రయోజనాలను తెలపండి.
జవాబు.

1. మధ్యగతం దృఢంగా నిర్వచింపబడుతుంది.
2. ఒక శ్రేణిలో గల అంశాలలో ఒక అంశం విలువ ఇతర అంశాల విలువలకు భిన్నంగా అత్యధికంగా ఉన్నప్పటికినీ మధ్యగతం విపరీత అంశాల విలువలచే ప్రభావం కాదు.
3. మధ్యగతాన్ని రేఖాచిత్రం ద్వారా కూడా గణన చేయడానికి వీలు కలుగుతుంది.
4. మధ్యగతాన్ని అర్థం చేసుకోవడం, గణించడం చాలా సులభం.

ప్రశ్న 10.
మధ్యగతం యొక్క పరిమితులను తెలపండి.
జవాబు.

1. మధ్యగతం – స్థానపు సగటు కాబట్టి, దాని గణన శ్రేణిలోని ప్రతి అంశం యొక్క విలువపైన ఆధారపడి ఉండదు. కాబట్టి మధ్యగతం విలువ శ్రేణిలో గల అంశాలకు ప్రాతినిధ్యం వహిస్తుందని చెప్పలేం.
2. మధ్యగతం తదుపరి బీజగణిత విశ్లేషణకు ఉపయోగపడదు.
3. అవిచ్ఛిన్న శ్రేణులలో దీనిని అంతర్వేశనం (Interpolated) చేయాల్సి ఉంటుంది.
4. సరిసంఖ్య గల అంశాలు శ్రేణిలో ఉన్నప్పుడు, రెండు మధ్య విలువల అంక మధ్యమమే మధ్యగతం అవుతుంది.

ప్రశ్న 11.
బహుళకం యొక్క ప్రయోజనాలను తెలపండి.
జవాబు.

1. బహుళకం శ్రేణులలో అధిక పర్యాయాలు కనిపించే విలువ. మధ్యగతం మాదిరి దీని విలువ విడిగా (isalated) ఉండదు, శ్రేణిలోలేని అంశాల విలువను తెలిపే అంకమధ్యమంలాగా ఉండదు.
2. విపరీత అంశాల ప్రభావం దీనిపై ఉండదు. అందువల్ల ఇది శ్రేణిలోని అంశాలకు ప్రాతినిధ్యం వహించును.
3. రేఖా చిత్రం ద్వారా కూడా బహుళకాన్ని లెక్కించవచ్చు.
4. విస్తృత అవధులు ఉన్న తరగతులలో కూడా బహుళకాన్ని లెక్కించవచ్చు.
5. దత్తాంశంలోని గుణాత్మక విలువలను వర్గీంచవలసినపుడు ఈ పద్ధతి ఉపయుక్తంగా ఉంటుంది.
6. బహుళకాన్ని అర్థం చేసుకోవడం, గణించడం సులభం.
7. ఇది నిత్య జీవితంలో తరచుగా ఉపయోగించే సగటు. ఉదాహరణకు తరగతి మార్కుల సగటు, ఒక విభాగంలో విద్యార్థుల సంఖ్యను కనుగొనుట మొదలైనవి.

ప్రశ్న 12.
బహుళకం యొక్క పరిమితులను తెలపండి.
జవాబు.

1. ద్విబహుళకం, బహుళ బహుళకం శ్రేణులలో బహుళకాన్ని లెక్కించడం చాలా కష్టం.
2. కేంద్రీకృత విలువలపై మాత్రమే బహుళకం ఆధారపడుతుంది. బహుళకం విలువ కంటే అధిక విలువలు కలిగిన ఇతర అంశాలు ఉన్నా అవి పరిగణింపబడవు. అవిచ్ఛిన్న శ్రేణులలో కేవలం తరగతి అంతరాల అవధులు మాత్రమే పరిగణింపబడతాయి.
3. బహుళకం ప్రతిచయన మార్పులకు ఎక్కువగా గురవుతుంది.
4.  బహుళకాన్ని వివిధ పద్ధతులలో లెక్కించినపుడు అంక మధ్యమం వలె ఒకే విలువ రాదు. గణనకు అనేక సూత్రాలు ఉన్నాయి. ఏది ఉపయోగించాలి అని సందేహం తలెత్తుతుంది.
5. ఇది బీజీయ ప్రస్తావనకు పనికి రాదు. అంకమధ్యమం వలె ఉమ్మడి బహుళక గణన సాధ్యం కాదు.
6. శ్రేణిలోని అంశాల సంఖ్య అత్యధికంగా ఉన్నప్పుడే బహుళకం ఆ శ్రేణిలోని విలువలకు ప్రాతినిధ్యం వహిస్తుంది.

ప్రశ్న 13.
ఈ కింది దత్తాంశానికి బహుళకం విలువను కనుగొనండి.

జవాబు.
ఇచ్చిన దత్తాంశం ప్రకారం ₹ 480 మూడు సార్లు వచ్చింది. కనుక బాహుళకం = 480.

ప్రశ్న 14.
హరమధ్యమం భానవ గురించి తెల్పండి.
జవాబు.
ఇచ్చిన శ్రేణిలోని అంశాల వ్యుత్రమాల (reciprocal) అంక మధ్యమానికి వ్యుత్రమమే ఆ అంశాల హరమధ్యమం. ఇంకొక విధంగా చెప్పాలంటే అంశాల సంఖ్యను, వాటి వ్యుత్రమాల మొత్తంచే భాగించగా వచ్చిన ఫలితమే హరమధ్యమం. దీనిని దిగువ తెలిపిన సమీకరణం ద్వారా కనుగొనవచ్చు.

H.M. = Reci \(\frac{\frac{1}{\mathrm{X}_1}+\frac{1}{\mathrm{X}_2}+\ldots .+\frac{1}{\mathrm{X}_{\mathrm{n}}}}{\mathrm{N}}\) లేదా
= \(\frac{\mathrm{N}}{\frac{1}{\mathrm{X}_1}+\frac{1}{\mathrm{X}_2}+\ldots \ldots+\frac{1}{\mathrm{X}_{\mathrm{n}}}}\) లేదా
= \(\frac{\mathrm{N}}{\sum\left(\frac{1}{\mathrm{X}}\right)}\)

ప్రశ్న 15.
4, 6, 12ల హరమధ్యమం విలువను లెక్కించండి.
జవాబు.
హరమధ్యమం విలువ = 4, 6, 12

N	X
1	4
2	6
3	12

∴ హరమధ్యమం (\(\frac{1}{x}\))
\(\frac{1}{4}\) = 0.2500;
\(\frac{1}{6}\) = 0.1667;.
\(\frac{1}{12}\) = 0.8333.

ప్రశ్న 16.
4, 16ల గుణమధ్యమం విలువను లెక్కించండి.
జవాబు.
గుణమధ్యమం విలువ : 4, 16

N	X
1	4
2	16

N = 2
గుణమధ్యమం = \(\sqrt[N]{x_1 \cdot x_2 \cdot x_3}=\left(x_1, x_2 \ldots \ldots x_4\right)^n\)
= \(\sqrt{4 \times 16}=\sqrt{64}\) = 8.

Textual Examples:

ప్రశ్న 1.
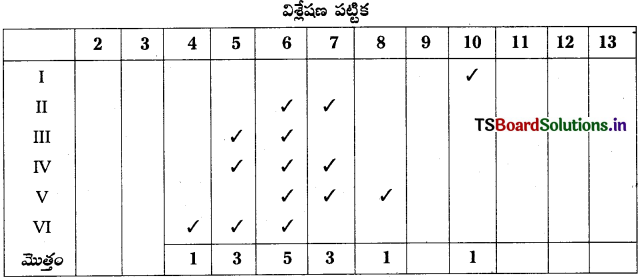
ఒక కళాశాలలో విదేశీ భాషలను చదువుతున్న విద్యార్థుల వివరాలు కింది పట్టికలో ఇవ్వడమైంది. ఈ దత్తాంశం సహాయంతో బహుళ బార్ పటాన్ని గీయండి.
పట్టిక : విదేశీ భాషలను చదువుతున్న విద్యార్థులు

సాధన.

ప్రశ్న 2.
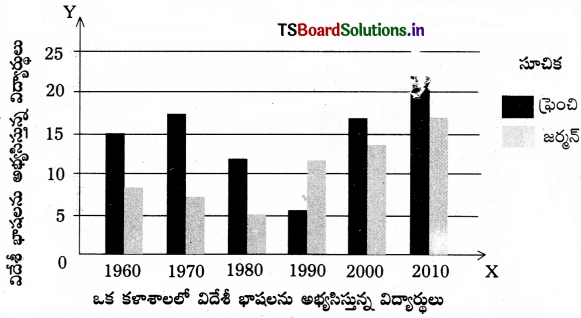
క్రింది దత్తాంశానికి ‘పై’ (Pie) చిత్రము గీయండి.

సాధన.

మొత్తం విస్తీర్ణం = 16 + 24 + 10 + 8 + 5 = 63
మొత్తం భూవిస్తీర్ణాన్ని డిగ్రీలలోకి మార్చినట్లయితే =
వరి = \(\frac{16 \times 360}{63}\) = 91°
గోధుమ= \(\frac{24 \times 360}{63}\) = 137°
రాగులు = \(\frac{10 \times 360}{63}\) = 57°
జొన్నలు = \(\frac{16 \times 360}{63}\) = 46°
తృణ ధాన్యాలు = \(\frac{5 \times 360}{63}\) = 29°
∴ మొత్తం = 360°.

ప్రశ్న 3.
దిగువ తెలిపిన దత్తాంశం బడికి వెళ్తున్న, బడి మానేసిన బాల బాలికలకు సంబంధించింది. ఈ దత్తాంశానికి శాతపు బార్ పటాన్ని గీయండి.

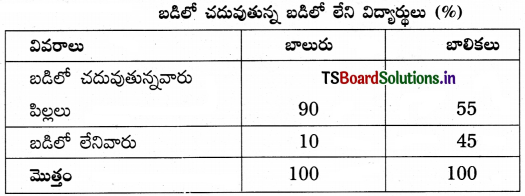
సాధన.

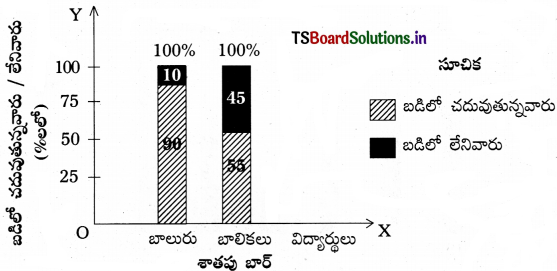
ప్రశ్న 4.
దిగువ ఇచ్చిన దత్తాంశం ఆరుగురు విద్యార్థులు ఒక పరీక్షలో పొందిన మార్కులకు సంబంధించింది అంక మధ్యమాన్ని గణన చేయండి.
మార్కులు (X): 70, 80, 40, 50, 65, 45
సాధన.

క్రమ సంఖ్య	X
1	70
2	80
3	40
4	50
5	65
6	45
N = 6	ΣX = 350

\(\overline{\mathrm{X}}=\frac{\Sigma \mathrm{X}}{\mathrm{N}}=\frac{350}{6}\) = 58.3

∴ \(\overline{\mathrm{X}}\) = 58.3.

ప్రశ్న 5.
కింది దత్తాంశానికి అంక మధ్యమాన్ని గణన చేయండి.

సాధన.

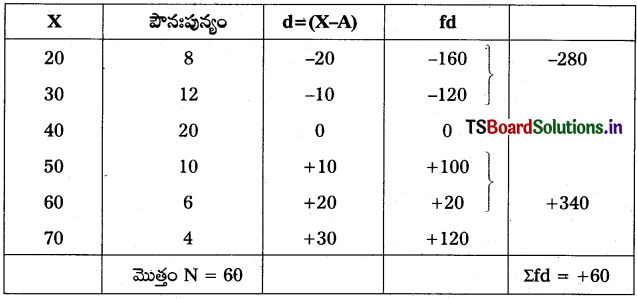
గమనిక : పై సమస్య సాధనలో ఊహించిన సగటు (A) 40గా తీసుకోబడింది.
\(\bar{X}=A+\frac{\sum \mathrm{fd}}{N}\)
ఇక్కడ, N = 60, Σfd = 60, A = 40 ఈ విలువలను పై సూత్రంలో ప్రతిక్షేపిస్తే,
\(\overline{\mathrm{X}}\) = 40 + \(\frac{60}{60}\)
= 40 + 1 = 41
∴ \(\overline{\mathrm{X}}\) = 40 + 1 = 41.

ప్రశ్న 6.
క్రింది దత్తాంశానికి అంక మధ్యమాన్ని కనుగొనండి.

సాధన.

\(\overline{\mathrm{X}}=\mathrm{A}+\frac{\sum \mathrm{fd}^{\prime}}{\mathrm{N}} \times \mathrm{C}^{\prime}\)

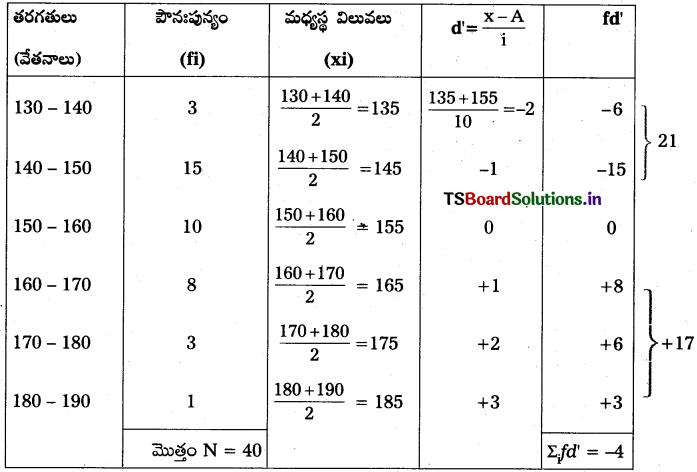
ఇక్కడ, \(\overline{\mathrm{X}}\) = అంక మధ్యమం
A = ఊహించిన అంక మధ్యమం = 155
Σ fd’ = ఊహించిన అంక మధ్యమం నుంచి తీసుకొన్న సోపాన విచలనాలను [d_i = \(\frac{\mathbf{x}_{\mathbf{i}}-\mathbf{A}}{\mathbf{i}}\)]
వాటి అనురూప పౌనఃపున్యాలతో గుణించగా వచ్చిన లబ్ధాల సంకలనం = – 4
N = పౌనఃపున్యాల = 40
C = తరగతి అంతరం = 10
ఈ విలువలను పై సూత్రంలో ప్రతిక్షేపిస్తే,
= 155 + \(\frac{-4}{40 \overline{\mathrm{X}}}\) × 10
= 155 + \(\frac{-40}{40}\)
= 155 – 1 = 154.
∴ \(\overline{\mathrm{X}}\) = 154.

ప్రశ్న 7.
కింది దత్తాంశం ఏడుగురు వ్యక్తుల ఆదాయాలకు సంబంధించింది. మధ్యగతాన్ని గణన చేయండి.
ఆదాయాలు (X) : 100 150 80 90 160 200
సాధన.
ఇవ్వబడిన దత్తాంశాన్ని ఆరోహన క్రమంలో రాయగా,

ఇక్కడ, Med = మధ్యగతం,
N = అంశాల సంఖ్య = 7
M = \(\left(\frac{7+1}{2}\right)^{\text {th }}=\frac{8}{2}\) = 4 వ సంఖ్య
4వ అంశానికి అనురూపంగా ఉన్న విలువ = 140,
కాబట్టి ∴ మధ్యగతం = 140.

ప్రశ్న 8.
కింది దత్తాంశానికి మధ్యగతాన్ని లెక్కించండి.

సాధన.

x	f	cf (సంచిత పౌనఃపున్యం)
10	5	5
20	8	13
30	12	25
40	20	45
50	30	75
60	16	91
70	10	101
80	7	108
90	8	116
	N = 116

 

మధ్యగత స్థానం = \(\left(\frac{\mathrm{N}+1}{2}\right)\)వ అంశం
ఇక్కడ, N = పౌనఃపున్యాల మొత్తం = 116
= \(\left(\frac{116+1}{2}\right)\) వ అంశం
= \(\frac{117}{2}\)వ అంశం
= 58.5 వ అంశం
58.5 వ అంశం పౌనఃపున్యం 75లో ఉంది. అందువల్ల దాని అనురూప ‘X’ విలువ 50 మధ్య అవుతుంది.
∴ మధ్యగతం = 50.

ప్రశ్న 9.
కింది దత్తాంశానికి మధ్యగతాన్ని లెక్కించండి.

సాధన.
మార్కులు విద్యార్థులు సాధన. పై దత్తాంశం విలీన (inclusive) శ్రేణులకు చెందింది. దీన్ని మినహాయింపు (exclusive) శ్రేణులలోకి మార్చి రాయాలి. ఇందుకోసం తరగతిలో ప్రతి దిగువ అవధిలో నుంచి 0.5 తీసివేయాలి. అలాగే ఎగువ అవధికి 0.5ను కలపాలి. అలా చేయడం ద్వారా విలీన శ్రేణులను మినహాయింపు (exclusive) శ్రేణులుగా మార్చవచ్చు. పై దత్తాంశాన్ని అలా మార్చి రాయగా,

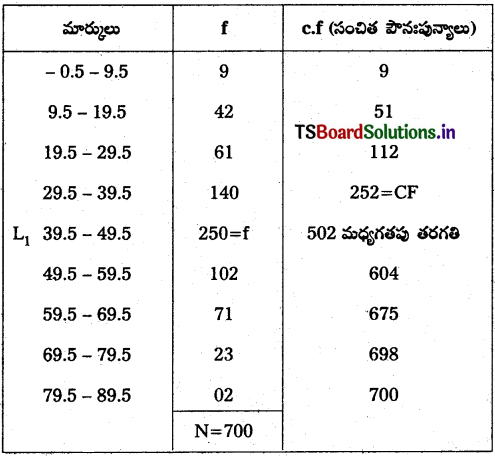
350 వ అంశం సంచిత పౌనఃపున్యం 502 తో ఉంది. దాని అనురూపమైన తరగతి 39.5 – 49.3 కాబట్టి మధ్యగతం విలువ ఈ మధ్యగత తరగతి 39.5 – 49.5 లో ఉంటుంది.
Med = L₁ + \(\left[\frac{\frac{\mathrm{N}}{2}-\mathrm{CF}}{\mathrm{f}}\right]\) × i
ఇక్కడ, Med = Median
L₁ = 39.5,
\(\frac{\mathrm{N}}{2}\) = 350
CF = 252
F = 250
i = 10
విలువలను పై సూత్రంలో ప్రతిక్షేపిస్తే,
= 39.5 + \(\frac{350-252}{250}\) × 10
= 39.5 + \(\frac{98}{250}\) × 10
= 39.5 + \(\frac{980}{250}\)
= 39.5+ 3.93 = 43.42
∴ మధ్యగతం = 43.42.

ప్రశ్న 10.
కింది దత్తాంశానికి బాహుళకాన్ని లెక్కించండి.

సాధన.

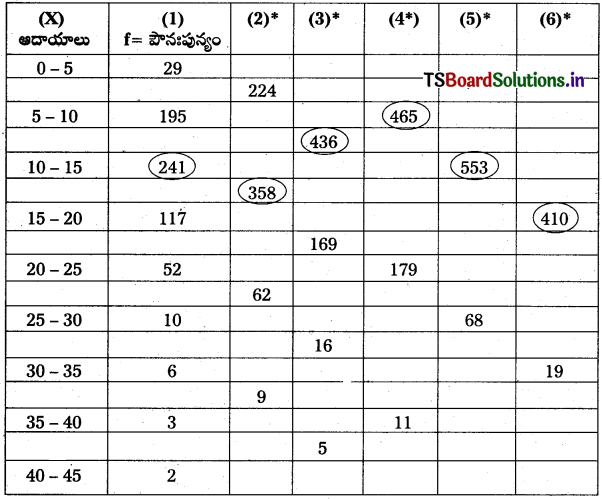
(2)* = ప్రతి రెండు అడ్డు వరుసలలో గల పౌనఃపున్యాల సంకలనం.
(3)* = మొదటి అడ్డు వరుసలో గల పౌనఃపున్యాన్ని వదిలి, ప్రతి రెండు అడ్డు వరుసల పౌనఃపున్యాల సంకలనం.
(4)* = ప్రతి మూడు అడ్డు వరుసలలో గల పౌనఃపున్యాల సంకలనం.
(5)* = మొదటి అడ్డు వరుసలో గల పౌనఃపున్యాన్ని వదిలి ప్రతి మూడు అడ్డు వరుసలతో పౌనఃపున్యాల సంకలనం.
(6)* = మొదటి రెండు అడ్డు వరుసలను వదిలి ప్రతి మూడు అడ్డు వరుసల పౌనఃపున్యాల సంకలనం.

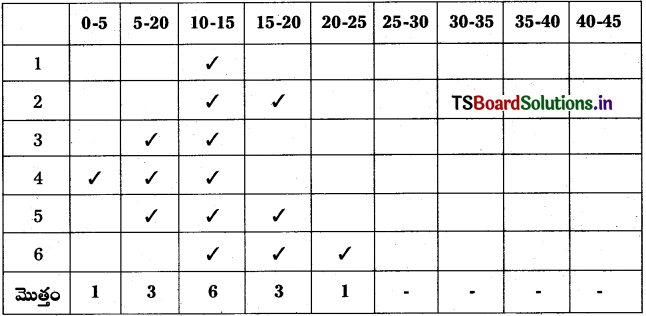
వర్గీకృత పట్టిక, విశ్లేషణ పట్టిక ప్రకారం 10-15 తరగతి ఎక్కువ పర్యాయాలు కనిపించింది. కాబట్టి బహుళకపు విలువ 10 – 15 తరగతిలో ఉంటుంది.

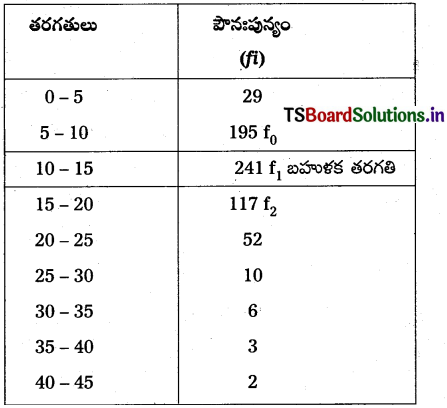
వర్గీకృతం మరియు విశ్లేషణ తర్వాత బహుళకం కనుగొనడానికి ఈ కింది ఫార్మలా ఉపయోగించుతాయి.
Z = L₁ + \(\frac{\Delta_1}{\Delta_1+\Delta_2}\) × i
ఇక్కడ, Z = బహుళకం = ?
L₁ = బహుళ తరగతి దిగువ అవధి = 10
f₀ = బహుళక తరగతికి ముందున్న తరగతి పౌనఃపున్యం = 195
f₁ = బహుళక తరగతి పౌనఃపున్యం = 241
f₂ = బాహుళక తరగతి తరువాత తరగతి పౌనఃపున్యం = 117
i తరగతి అంతరం = 5
∆₁ = f₁ – f₀
= 241 – 195 = 46
∆₂ = f₁ – f₂
= 241 – 117 = 124
విలువలను పై సూత్రంలో ప్రతిక్షేపిస్తే,
= 10 + \(\frac{46}{46+124}\) × 5
= 10 + \(\frac{230}{170}\)
= 10 + 1.35
= 11.35
∴ Z = 11.35.