TS Inter 1st Year Maths 1B Direction Cosines and Direction Ratios Important Questions

Students must practice these Maths 1B Important Questions TS Inter 1st Year Maths 1B Direction Cosines and Direction Ratios Important Questions to help strengthen their preparations for exams.

TS Inter 1st Year Maths 1B Direction Cosines and Direction Ratios Important Questions

Question 1.
Find the direction cosines of two lines that are connected by the relations l + m + n = 0 and mn – 2nl – 2lm = 0. [Mar. ’17 (TS), ’11, ’04; May ’15 (TS)]
Solution:
Given that, l + m + n = 0 …….(1)
mn – 2nl – 2lm = 0 ……….(2)
From (1), l = -m – n
Substituting (l) in (2),
mn – 2n(-m – n) – 2(-m – n)m = 0
mn + 2mn + 2n² + 2m² + 2mn = 0
2m² + 5mn + 2n² = 0
2m² + 4mn + mn + 2n² = 0
2m(m + 2n) + n(m + 2n) = 0
(m + 2n)(2m + n) = 0
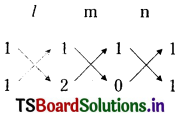
m + 2n = 0 ……..(3)
2m + n = 0 ………(4)
Solving (1) & (3)

Question 2.
Find the direction cosines of two lines that are connected by the relations l – 5m + 3n = 0 and 7l² + 5m² – 3n² = 0. [Mar. ’18 (AP); Mar. ’16 (TS); May ’09]
Solution:
Given that,
l – 5m + 3n = 0 ……….(1)
7l² + 5m² – 3n² = 0 …………(2)
From (1), l = 5m – 3n
Substituting ‘l’ in (2)
7(5m – 3n)² + 5m² – 3n² = 0
7(25m² + 9n² – 30mn) + 5m² – 3n² = 0
175m² + 63n² – 210mn + 5m² – 3n² = 0
180m² – 210mn + 60n² = 0
6m² – 7mn + 2n² = 0
2m(3m – 2n) – n(3m – 2n) = 0
(3m – 2n) (2m – n) = 0
3m – 2n = 0 ………(3)
2m – n = 0 ………. (4)
Solving (1) & (3)

Question 3.
Show that the lines whose direction cosines are given by l + m + n = 0, 2mn + 3nl – 5lm = 0 are perpendicular to each other. [Mar. ’16 (AP); ’12]
Solution:
Given that, l + m + n = 0 ……….(1)
2mn + 3nl – 5lm = 0 ……….(2)
From (1), l = -m – n
Substituting in (2)
2mn + 3n(-m – n) – 5(-m – n)m = 0
2mn – 3mn – 3n² + 5m² + 5mn = 0
5m² + 4mn – 3n² = 0
If ax² + 2hxy + by² = 0 represents a pair of straight lines then the two lines are


Direction ratio’s of 2nd line are (a2, b2, c2) = (-3 – √19, -2 + √19, 5)
Now, a₁a₂ + b₁b₂ + c₁c₂ = (-3 + √19) (-3 – √19) + (-2 – √19)(-2 + √19) + 5(5)
= (-3)² – (√19)² + (-2)² – (√19)² + 25
= 9 – 19 + 4 – 19 + 25
= 38 – 38
= 0
∴ The two lines are perpendicular to each other.

Question 4.
Find the angle between the lines whose direction cosines satisfy the equations l + m + n = 0, l² + m² – n² = 0. [Mar. ’17 (AP), ’13, ’07 ; May ’14, ’13 (Old), ’11, ’07, ’04; Mar. ’19 (AP&TS)]
Solution:
Given that
l + m + n = 0 ……….(1)
l² + m² – n² = 0 ……….(2)
From (1), l = -m – n
Substituting in (2)
(-m – n)² + m² – n² = 0
m² + n² + 2mn + m² – n² = 0
2m² + 2mn = 0
2m(m + n) = 0
2m = 0
m = 0 ………(3)
m + n = 0 ……….(4)
Solving (1) & (3)

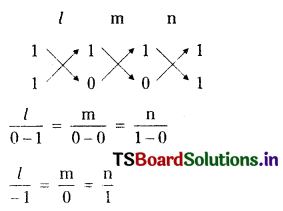
∴ The direction ratios of 1st line are (a₁, b₁, c₁) = (-1, 0, 1).
Solving (1) & (4)

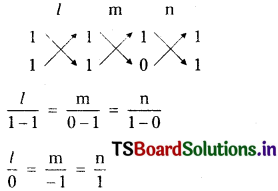
∴ The direction ratios of the 2nd line are (a₂, b₂, c₂) = (0, -1, 1).
Now, if ‘θ’ is the angle between these two lines then

∴ θ = 60°

Question 5.
Find the angle between the lines whose direction cosines are given by the equations 3l + m + 5n = 0 and 6mn – 2nl + 5lm = 0. [Mar. ’12, ’10, ’06; May ’15 (AP); ’10]
Solution:
Given that,
3l + m + 5n = 0 ……….(1)
6mn – 2nl + 5lm = 0 ………..(2)
From (1), m = -3l – 5n
Substituting in (2)
6n(-3l – 5n) – 2ln + 5l(-3l – 5n) = 0
-18ln – 30n² – 2ln – 15l² – 25ln = 0
-15l² – 45ln – 30n² = 0
l² + 3ln + 2n² = 0
l² + 2ln + ln + 2n² = 0
(l + n)(l + 2n) = 0
l + 2n = 0 ………(3)
l + n = 0 ……….(4)
Solving (1) & (3)

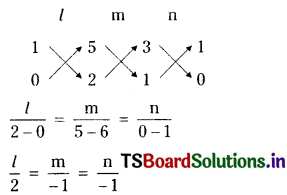
∴ Direction ratio s of 1st line are (a₁, b₁, c₁) = (2, -1, -1)
Solving (1) & (4)

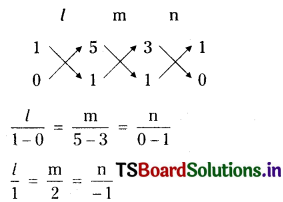
∴ Direction ratio’s of 2nd line are (a₂, b₂, c₂) = (1, 2, -1)
Now, if ‘θ’ is the angle between these two lines then

Question 6.
If a ray makes angles α, β, γ, δ with the four diagonals of a cube, find cos²α + cos²β + cos²γ + cos²δ. [Mar. ’08, ’05; May ’05; B.P.]
Solution:

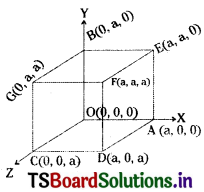
Let one vertex of the cube as origin ‘O’ and 3 co-terminus edges OA, OB, OC as the coordinate axes.
Let ‘A’ be the edge of the cube. Then the coordinates of the vertices of the cube are O(0, 0, 0), A(a, 0, 0), B(0, a, 0), C(0, 0, a), D(a, 0, a), E (a, a, 0), F(a, a, a), G (0, a, a)
The four diagonals are \(\overline{\mathrm{OF}}, \overline{\mathrm{CE}}, \overline{\mathrm{AG}}, \overline{\mathrm{BD}}\).
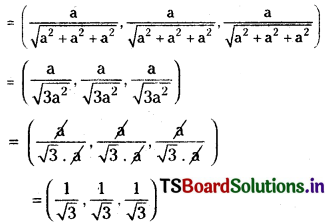
Direction Ratios of \(\overline{\mathrm{OF}}\) are (x₂ – x₁, y₂ – y₁, z₂ – z₁)
= (a – 0, a – 0, a – 0)
= (a, a, a)
Direction cosines of \(\overline{\mathrm{OF}}\) are

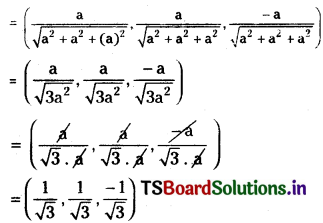
Direction ratios of \(\overline{\mathrm{CE}}\) are (x₂ – x₁, y₂ – y₁, z₂ – z₁)
= (a – 0, a – 0, 0 – a)
= (a, a, -a)
Direction cosines of \(\overline{\mathrm{CE}}\) are

Direction ratios of \(\overline{\mathrm{AG}}\) are (x₂ – x₁, y₂ – y₁, z₂ – z₁)
= (0 – a, a – 0, a – 0)
= (-a, a, a)
Direction cosines of \(\overline{\mathrm{AG}}\) are

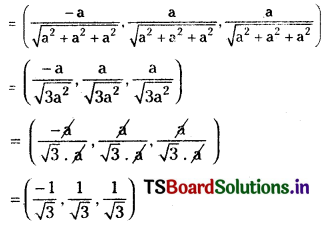
Direction ratios of \(\overline{\mathrm{BD}}\) are (x₂ – x₁, y₂ – y₁, z₂ – z₁)
= (a – 0, 0 – a, a – 0)
= (a, -a, a)
Direction cosines of \(\overline{\mathrm{BD}}\) are

Let (l, m, n) be the direction cosines of the line which makes angles α, β, γ, δ with the four diagonals \(\overline{\mathrm{OF}}, \overline{\mathrm{CE}}, \overline{\mathrm{AG}}, \overline{\mathrm{BD}}\) of the cube.
Similarly,

Question 7.
Find the angle between two diagonals of a cube. [Mar. ’18 (TS); Mar. ’15 (AP); May ’13]
Solution:

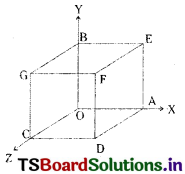
Let one vertex of the cube as origin ‘O’ and 3 co-terminus edges OA, OB, OC as the coordinate axes.
Let ‘A’ be the edge of the cube. Then the coordinates of the vertices of the cube are O(0, 0, 0), A(a, 0, 0), B(0, a, 0), C(0, 0, a), D(a, 0, a), E (a, a, 0), F(a, a, a), G (0, a, a)
Direction ratios of \(\overline{\mathrm{OF}}\) are (x₂ – x₁, y₂ – y₁, z₂ – z₁)
= (a – 0, a – 0, a – 0)
= (a, a, a)
Direction ratios of \(\overline{\mathrm{BD}}\) are (x₂ – x₁, y₂ – y₁, z₂ – z₁)
= (a – 0, 0 – a, a – 0)
= (a, -a, a)
If ‘θ’ is the angle between diagonals \(\overline{\mathrm{OF}}\) & \(\overline{\mathrm{BD}}\) then,
cos θ = \(\frac{\left|\mathrm{a}_1 \mathrm{a}_2+\mathrm{b}_1 \mathrm{~b}_2+\mathrm{c}_1 \mathrm{c}_2\right|}{\sqrt{\mathrm{a}_1^2+\mathrm{b}_1^2+\mathrm{c}_1^2} \sqrt{\mathrm{a}_2^2+\mathrm{b}_2^2+\mathrm{c}_2^2}}\)

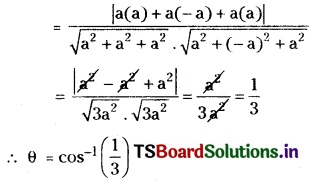
Similarly, the angle between any pair of diagonals can be found to be \(\cos ^{-1}\left(\frac{1}{3}\right)\).

Question 8.
The vertices of a triangle are A(1, 4, 2), B(-2, 1, 2), C(2, 3, -4). Find ∠A, ∠B, ∠C.
Solution:
A(1, 4, 2), B(-2, 1, 2), C(2, 3, -4) are the given vertices of a triangle.

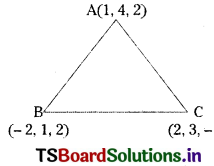
Direction ratios of \(\overline{\mathrm{AB}}\) are (-2 – 1, 1 – 4, 2 – 2) = (-3, -3, 0) = (1, 1, 0)
Direction ratios of \(\overline{\mathrm{BC}}\) are (2 + 2, 3 – 1, -4 – 2) = (4, 2, -6) = (2, 1, -3)
Direction ratios of \(\overline{\mathrm{CA}}\) are (1 – 2, 4 – 3, 2 + 4) = (-1, 1, 6)
If A is the angle between the sides \(\overline{\mathrm{AB}}\), \(\overline{\mathrm{CA}}\) then,

∴ A = 90°
If B is the angle between the sides \(\overline{\mathrm{AB}}\), \(\overline{\mathrm{BC}}\) then,
cos B = \(\left|\frac{1(2)+1(1)+0(-3)}{\sqrt{1^2+1^2+0^2} \sqrt{2^2+1^2+(-3)^2}}\right|\)

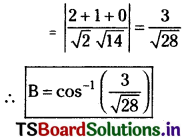
If c is the angle between the sides \(\overline{\mathrm{BC}}\), \(\overline{\mathrm{CA}}\) then,

Question 9.
If P(2, 3, -6), Q(3, -4, 5) are two points, find the direction cosines of \(\overline{\mathbf{O P}}, \overline{\mathbf{Q O}}\) and \(\overline{\mathbf{P Q}}\) where ‘O’ is the origin. [Mar. ’00]
Solution:
O(0, 0, 0), P(2, 3, -6), Q(3, -4, 5) are the given points.
Direction ratios of \(\overline{\mathbf{OP}}\) are (x₂ – x₁, y₂ – y₁, z₂ – z₁)
= (2 – 0, 3 – 0, -6 – 0)
= (2, 3, -6)
= (a, b, c)
Direction cosines of \(\overline{\mathbf{OP}}\) are

Direction ratios of \(\overline{\mathbf{OQ}}\) are (x₂ – x₁, y₂ – y₁, z₂ – z₁)
= (-3 + 0, +4 + 0, -5 + 0)
= (-3, +4, -5)
= (a, b, c)
Direction cosines of \(\overline{\mathbf{OQ}}\) are

Direction ratios of \(\overline{\mathbf{PQ}}\) are (x₂ – x₁, y₂ – y₁, z₂ – z₁)
= (3 – 2, -4 – 3, 5 + 6)
= (1, -7, 11)
= (a, b, c)
Direction cosines of \(\overline{\mathbf{PQ}}\) are

Question 10.
A ray makes angles \(\frac{\pi}{3}, \frac{\pi}{3}\) with \(\overline{\mathbf{OX}}\) and \(\overline{\mathbf{OY}}\) respectively. Find the angle made by it with \(\overline{\mathbf{OZ}}\). [May ’02]
Solution:
Let α, β, γ be the angles made by the line with the positive x, y, z axis respectively.
Given that, α = 60°, β = 60°
But, cos²α + cos²β + cos²γ = 1
cos²60° + cos²60° + cos²60° = 1

γ = 45° (or) γ = 135°

Question 11.
Find the direction cosines of the line joining the points (-4, 1, 7) and (2, -3, 2). [May ’02]
Solution:
Let A = (-4, 1, 7), B = (2, -3, 2) are the given points.
Direction ratios of \(\overline{\mathrm{AB}}\) are (x₂ – x₁, y₂ – y₁, z₂ – z₁)
= (2 + 4, -3 – 1, 2 – 7)
= (6, -4, -5)
= (a, b, c)
Direction cosines of \(\overline{\mathrm{AB}}\) are

Question 12.
Find the direction ratios and direction cosines of the line joining the points (4, -7, 3), (6, -5, 2). [Mar’ 00]
Solution:
Let A = (4, -7, 3), B = (6, -5, 2) are the given points.
Direction ratios of \(\overline{\mathrm{AB}}\) are (x₂ – x₁, y₂ – y₁, z₂ – z₁)
= (6 – 4, -5 + 7, 2 – 3)
= (2, 2, -1)
= (a, b, c)
Direction cosines of \(\overline{\mathrm{AB}}\) are

Question 13.
Show that the line joining the points A(2, 3, -1) and B(3, 5, -3) is perpendicular to the lines joining C(1, 2, 3) and D(3, 5, 7). [Mar. ’03]
Solution:
A = (2, 3, -1), B = (3, 5, -3), C = (1, 2, 3), D = (3, 5, 7) are the given points.
Direction ratios of \(\overline{\mathrm{AB}}\) are (x₂ – x₁, y₂ – y₁, z₂ – z₁)
= (3 – 2, 5 – 3, -3 + 1)
= (1, 2, -2)
= (a₁, b₁, c₁)
Direction ratios of \(\overline{\mathrm{CD}}\) are (x₂ – x₁, y₂ – y₁, z₂ – z₁)
= (3 – 1, 5 – 2, 7 – 3)
= (2, 3, 4)
= (a₂, b₂, c₂)
Now, a₁a₂ + b₁b₂ + c₁c₂ = 1(2) + 2(3) + (-2) 4
= 2 + 6 – 8
= 8 – 8
= 0
∴ \(\overline{\mathrm{AB}}\) is perpendicular to \(\overline{\mathrm{CD}}\).

Question 14.
Find the angle between the lines whose direction ratio’s are (1, 1, 2) (√3, -√3, 0).
Solution:
Given that, the direction ratios of two lines are (a₁, b₁, c₁) = (1, 1, 2) and (a₂, b₂, c₂) = (√3, -√3, 0)
If ‘θ’ is the angle between these two lines then
cos θ = \(\frac{\left|a_1 a_2+b_1 b_2+c_1 c_2\right|}{\sqrt{a_1^2+b_1^2+c_1^2} \sqrt{a_2^2+b_2^2+c_2^2}}\)

Question 15.
Find the angle between \(\overline{\mathrm{DC}}\) and \(\overline{\mathrm{AB}}\) where A = (3, 4, 5), B = (4, 6, 3), C = (-1, 2, 4) and D = (1, 0, 5). [Mar. ’06]
Solution:
A = (3, 4, 5), B = (4, 6, 3), C = (-1, 2, 4), D = (1, 0, 5) are the given points.
Direction ratios of \(\overline{\mathrm{AB}}\) are (x₂ – x₁, y₂ – y₁, z₂ – z₁)
= (4 – 3, 6 – 4, 3 – 5)
= (1, 2, -2)
= (a₁, b₁, c₁)
Direction ratios of \(\overline{\mathrm{DC}}\) are (x₂ – x₁, y₂ – y₁, z₂ – z₁)
= (1 + 1, 0 – 2, 5 – 4)
= (2, -2, 1)
= (a₂, b₂, c₂)
If ‘θ’ is the angle between the lines \(\overline{\mathrm{AB}}\) & \(\overline{\mathrm{DC}}\) then,

Some More Maths 1B Direction Cosines and Direction Ratios Important Questions

Question 1.
Find the direction cosines of a line that makes equal angles with the axes.
Solution:
If α, β, γ be the angles made by the line with the axis.
Since the line is equally inclined to the axis, then α = β = γ then
cos α = cos β = cos γ
We know that,
cos²α + cos²β + cos²γ = 1
cos²α + cos²α + cos²α = 1
3 cos²α = 1
cos²α = \(\frac{1}{3}\)
cos α = \(\pm \frac{1}{\sqrt{3}}\)
∴ The direction cosines of the lines are \(\left(\pm \frac{1}{\sqrt{3}}, \pm \frac{1}{\sqrt{3}}, \pm \frac{1}{\sqrt{3}}\right)\)
The number of lines that are equally inclined to the axes is equal to the no.of different combinations of signs with l, m, n are possible = 4.

Question 2.
If the directions of a line are \(\left(\frac{1}{\mathrm{c}}, \frac{1}{\mathrm{c}}, \frac{1}{\mathrm{c}}\right)\), find ‘c’.
Solution:
Given that, the direction cosines of a line are (l, m, n) = \(\left(\frac{1}{\mathrm{c}}, \frac{1}{\mathrm{c}}, \frac{1}{\mathrm{c}}\right)\)
We know that,
l² + m² + n² = 1
\(\frac{1}{c^2}+\frac{1}{c^2}+\frac{1}{c^2}\)
\(\frac{3}{\mathrm{c}^2}\) = 1
c² = 3
c = ±√3

Question 3.
If a line makes angles α, β, γ with the positive directions of x, y, and z-axes, what is the value of sin²α + sin²β + sin²γ?
Solution:
Since α, β, γ are the angles made by a line with the positive direction of co-ordinates axes, then
cos²α + cos²β + cos²γ = 1
Now, sin²α + sin²β + sin²γ
= (1 – cos²α) + (1 – cos²β) + (1 – cos²γ)
= 3 – (cos²α + cos²β + cos²γ)
= 3 – 1
= 2

Question 4.
Show that the line joining the points P(0, 1, 2) and Q(3, 4, 8) is parallel to the line joining the points R(-2, \(\frac{3}{2}\), -3) and S(\(\frac{5}{2}\), 6, 6).
Solution:
P = (0, 1, 2), Q = (3, 4, 8), R = (-2, \(\frac{3}{2}\), -3), S = (\(\frac{5}{2}\), 6, 6) are the given points.
Direction ratios of \(\overline{\mathrm{PQ}}\) are (x₂ – x₁, y₂ – y₁, z₂ – z₁)
= (3 – 0, 4 – 1, 8 – 2)
= (3, 3, 6)
= (a₁, b₁, c₁)
Direction ratios of \(\overline{\mathrm{RS}}\) are (x₂ – x₁, y₂ – y₁, z₂ – z₁)

∴ \(\overline{\mathrm{PQ}}\) is parallel to \(\overline{\mathrm{RS}}\).

Question 5.
A(1, 8, 4), B(0, -11, 4), C(2, -3, 1) are three points and D is the foot of the perpendicular from A to BC. Find the coordinates of D.
Solution:
A(1, 8, 4), B(0, -11, 4), C(2, -3, 1) are the given points.
D is the foot of the perpendicular from A to BC.
Suppose D divides \(\overline{\mathrm{BC}}\) in the ratio m : n then the co-ordinate of D.

Question 6.
‘O’ is the origin, P(2, 3, 4) and Q(1, k, 1) are points such that \(\overline{\mathrm{OP}} \perp \overline{\mathbf{O Q}}\). Find k.
Solution:
O(0, 0, 0), P(2, 3, 4), Q(1, k, 1) are the given points.
Direction ratio’s of \(\overline{\mathrm{OP}}\) are (x₂ – x₁, y₂ – y₁, z₂ – z₁)
= (2 – 0, 3 – 0, 4 – 0)
= (2, 3, 4)
= (a₁, b₁, c₁)
Direction ratio’s of \(\overline{\mathrm{OQ}}\) are (x₂ – x₁, y₂ – y₁, z₂ – z₁)
= (1 – 0, k – 0, 1 – 0)
= (1, k, 1)
= (a₂, b₂, c₂)
Since \(\overline{\mathrm{OP}} \perp \overline{\mathbf{O Q}}\) then,
a₁a₂ + b₁b₂ + c₁c₂ = 0
2(1) + 3(k) + 4(1) = 0
2 + 3k + 4 = 0
6 + 3k = 0
3k = -6
k = -2

Question 7.
If (l₁, m₁, n₁), (l₂, m₂, n₂) are the direction cosines of two intersecting lines, show that the direction cosines of two lines bisecting the angles between them are proportional to l₁ ± l₂, m₁ ± m₂, n₁ ± n₂.
Solution:

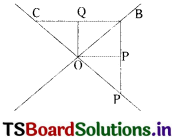
Let the two lines intersect at the origin ‘O’.
Let A and C be two different points on one line and B be a point on the other line such that
OA = OB = OC = 1
The co-ordinates of A, B, C are A(l₁, m₁, n₁), B(l₂, m₂, n₂), C(-l₁, -m₁, n₁)
Let P, Q be the midpoints of \(\overline{\mathrm{AB}} \& \overline{\mathrm{BC}}\) respectively.
Then OP & OQ are the required bisectors.
Since, P is the midpoint of \(\overline{\mathrm{AB}}\) then


∴The directions of the bisectors are proportional to (l₁ ± l₂, m₁ ± m₂, n₁ ± n₂)