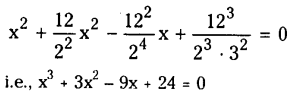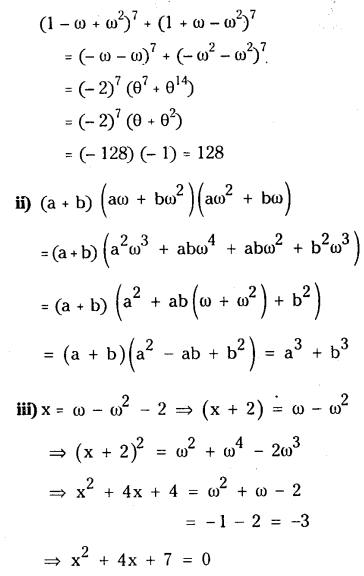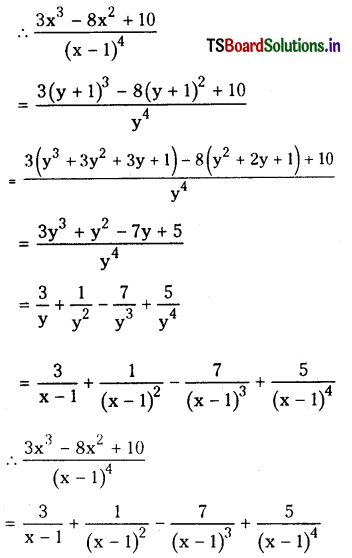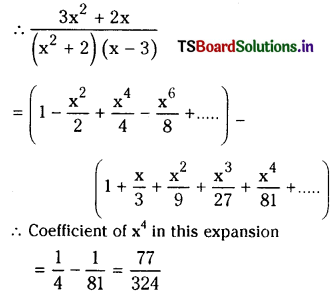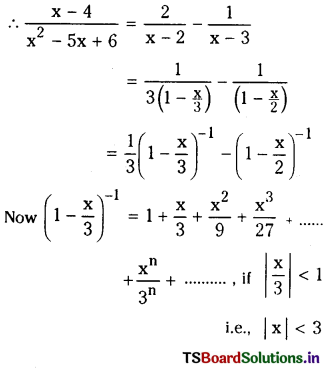TS Inter 2nd Year

Students must practice this TS Intermediate Maths 2B Solutions Chapter 8 Differential Equations Ex 8(a) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 8 Differential Equations Ex 8(a)

I.
Question 1.
Find the order of the differential equation obtained by eliminating the arbitrary constants b and c from xy = ce^x+ be^-x + x².
Solution:
Given equation is xy = ce^x + be^-x + x² ………….(1)
Differentiating (1) w.r.t x, we get
xy₁ + y = ce^x – be^-x + x²
Again differentiating w.r.t x, we get
xy₂ + y₁ + y₁ = ce^x + be^-x + 2
= (xy – x²) + 2
∴ xy₂ + 2y₁ – (xy – x²) – 2 = 0 ………………(2)
Arbitrary constants a and b are eliminated in the differential equation (2).
The order of the differential equation (2) is 2.

Question 2.
Find the order of the differential equation of the family of all circles with their cen¬tres at the origin.
Solution:
The equation of circle with centre 0 is given by x² + y² = a² where a is any constant.
Differentiating w.r.t x we get 2x + 2yy₁ = 0
⇒ x + yy₁ = 0
Which is the required differential equation of family of all circles with their centres at origin.
The order of the above differential equation is 1.

II.
Question 1.
Form the differential equations of the following family of curves where parameters are given in brackets.
(i) y = c (x – c)²; (c)
Given y = c(x – c)² ……………..(1)
Differentiating w.r.t ‘x’ we have
y₁ = 2c(x – c) ………….(2)

∴ y . y₁³ = (xy₁ – 2y) 4y²
⇒ y₁³ = (xy₁ – 2y) 4y
⇒ y₁³ = 4xyy₁ – 8y²
⇒ y₁³ – 4xyy₁ + 8y² = 0
⇒ \(\left(\frac{d y}{d x}\right)^3\) – 4xy \(\frac{d y}{d x}\) + 8y² = 0
This the differential equation in which c is eliminated.

ii) xy = ae^x + be^-x ; (a, b)
Solution:
Given xy = ae^x + be^-x and ………….(1)
Differentiating (1) w.r.t x
xy₁ + y = ae^x – be^-x
Again differentiating w.r.t x,
xy₂ + y₁ + y₁ = ae_x + be_-x = xy
= xy₂ + 2y₁ – xy = 0
which is the required equation obtained on the elimination of a and b.

(iii) y = (a + bx) e^kx; (a, b)
Solution:
Given y = (a + bx) e^kx …………(1)
and Differentiating (1) w.r.t x, we get
y₁ = (a + bx) ke^kx + e^kx . b
= ky + e^kx . b
∴ y₁ – ky = be^kx ………….(2)
Again differentiating w.r.t x,
y₂ – ky₁ = kbe^kx
= k(y₁ – ky)
⇒ y₂ – 2ky₁ + k²y = 0
⇒ \(\frac{d^2 y}{d x^2}-2 \mathrm{k} \frac{d y}{d x}\) + k²y = 0
is the required equation obtained on the elimination of a, b.

v) y = a cos (nx + b); (a, b)
Solution:
Given equation is y = a cos (nx + b)
∴ y₁ = – an sin (nx + b)
= – an² cos (nx + b)
= – n²y
∴ y₁ + n²y = 0
⇒ \(\frac{d^2 \mathrm{y}}{d x^2}\) + n²y = 0
is the required differential equation obtained on elimination of a and b.

Question 2.
Obtain the differential equation which corresponds to each of the following family of curves.
(i) The rectangular hyperbolas which have the coordinate axes as asymptotes.
Solution:
Equation of rectangular hyperbolas which have the coordinate axes as asymptotes is
xy = c².
Differentiating w.r.t x,
xy₁ + y = 0
⇒ x\(\frac{d y}{d x}\) + y = 0 is the required equation.

(ii) The ellipses with centres at the origin and having coordinate axes as axes.
Solution:
Equation of ellipse is \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1
Differentiating w.r.t x’ we get,

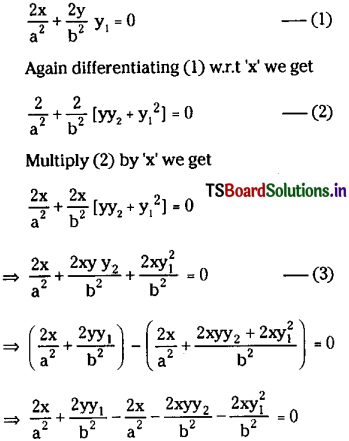
⇒ \(\frac{2}{\mathrm{~b}^2}\) [yy₁ – xyy₂ – xy₁²] = 0
⇒ yy₁ – xyy₂ – xy₁² = 0
⇒ xyy₂ + xy₁ – yy₁ = 0
⇒ \(x y \frac{d^2 y}{d x^2}+x\left(\frac{d y}{d x}\right)^2-y \frac{d y}{d x}=0\) is the required differential equation.

III.
Question 1.
Form the differential equations of the following family of curves whose parameters are given in brackets.
(i) y = ae^3x + be^4x; (a, b)
Solution:
Given y = ae^3x + be^4x
Differentiating w.r.t. ‘X’
y₁ = 3ae^3x + 4be^4x
⇒ y₁ – 3ae^3x = 4be^4x
= 4 [y – ae^3x]
⇒ y₁ – 4y = ae^3x ………….(1)
Again differentiating w.r.t. x,
y₂ – 4y₁ = – 3ae^3x
⇒ y₂ – 4y₁ = 3 (y₁ – 4y)
⇒ y₂ – 7y₁ + 12y = 0 is the required differential equation.

(ii) y = ax² + bx, (a, b)
Solution:
Given equation is
y = ax² + bx …………..(1)
and dill erentiating w.r.t. x
y₁ = 2ax + b …………(2)
Again differentiating w.r.t. x,
y₂ = 2a
⇒ x²y₂ = 2ax² …………..(3)
Also from (2)
– 2xy₁ = – 4x²a – 2bx …………..(4)
From (1)
2y = 2ax² + 2bx …………(5)
Adding (3), (4), (5) we get
x²y₂ – 2xy₁ + 2y = 2ax² – 4ax² – 2bx + 2ax² + 2bx = 0
∴ \(x^2 \frac{d^2 y}{d x^2}-2 x \frac{d y}{d x}+2 y=0\) is the required differential equation in which a, b are eliminated.

(iii) ax² + by² = 1; (a, b)
Solution:
Given equation of the curve is
ax² + by² = 1 ……………(1)
Differentiating (1) w.r.t. ‘x we get
2ax + 2by \(\frac{d y}{d x}\) = 0 and
by² = 1 – ax² from (1)
⇒ 2ax + 2byy₁ = 0 ……………(2)
⇒ b(2yy₁) = – 2ax …………….(3)
From (3) + (2) we get

⇒ – xay = y₁ (1 – ax²)
⇒ – axy = y₁ – ax²y₁
⇒ y₁ = ax (xy₁ – y)
⇒ a = \(\frac{y_1}{x\left(x y_1-y\right)}\)
Differentiating w.r.t x,
0 = \(\frac{d}{d x}\left[\frac{y_1}{x\left(x y_1-y\right)}\right]\)
= \(\frac{y_2\left(x^2 y_1-x y\right)-y_1\left(\frac{d}{d x}\left(x^2 y_1-x y\right)\right)}{x^2\left(x y_1-y\right)^2}\)
⇒ (x²y₁ – xy)y₂ – y₁(x²y₂ + 2xy₁ – xy₁ – y) = 0
⇒ x²y₁y₂ – xyy₁ – x²y₁y₂ – 2xy₁² + xy₁² + yy₁ = 0
⇒ xyy₂ + xy₁² – yy₁ = 0
⇒ \(x y \frac{d^2 y}{d x^2}+x\left(\frac{d y}{d x}\right)^2-y\left(\frac{d y}{d x}\right)\) = 0 is the required differential equation obtained on elimination of constants a and b.

(iv) xy = ax² + \(\frac{b}{x}\); (a, b)
Solution:
Given equation is x²y = ax³ + b ………….(1)
Differentiating (1) w.r.t. ‘x’
2xy + x²y₁ = 3ax² ………….(2)
Again differentiating w.r.t x,
x²y₂ + 2xy₁ + 2xy₁ + 2y = 6ax
⇒ x²y₂ + 4xy₁ + 2y = 6ax
⇒ x³y₂ + 4x2y₁ + 2xy = 6ax²
= 2(3ax²)
= 2 [2xy + x²y₁]
= 2x²y₁ + 4xy
⇒ x³y² + 2x²y₁ – 2xy = 0
⇒ x²y₂ + 2xy₁ – 2y = 0
⇒ \(x^2 \frac{d^2 y}{d x^2}+2 x \frac{d y}{d x}\) – 2y = 0 which is the required differential equation on elimination of constants a and b from (1).

Question 2.
Obtain the differential equation which corresponds to each of the following family of curves.
(i) The circles which touch the Y – axis at the origin.
Solution:
The cquation of circle which touch the Y-axis at the origin is x² + y² + 2gx = 0 ………..(1)
Differentiating wr.t. x we get
2x + 2yy₁ + 2g = 0
⇒ g = – (x + yy₁)
Hence from (1)
x² + y² + 2x [- (x + yy₁)] = 0]
x² + y² – 2x² – 2xyy₁ = 0
⇒ – y² – x² = 2xy . \(\frac{d y}{d x}\) which is the required differential equation obtained on elimination of ‘g’ from (1).

(ii) The parabola each of which has a laws rectum 4a and whose axis are parallel to X- axis.
Solution:
Equation of parabola which has latus rectum 4a and whose axes are parallel to X-axis is
(y – k)² = 4a(x – h) ………….(1)
Differentiating w.r.t ‘x’
2 (y – k) y₁ = 4a
⇒ (y – k) y₁ = 2a ……………(2)
Differentiating again w.r.t ‘x’
(y – k) y₂ + y₁² = 0
From (2)
y – k = \(\frac{2 a}{y_1}\)
∴ From (3)
\(\frac{2 a}{y_1}\) y₂ + y₁² = 0
⇒ 2ay₂ + y₁³ = 0
⇒ 2a \(\frac{d^2 y}{d x^2}+\left(\frac{d y}{d x}\right)^3\) = 0 which is the required differential equation obtained on elimination of constants h, k from (1).

(iii) The parabolas having their focli at the origin and axis along the X-axis.
Solution:
Equation of parabola having focii at origin and axis is along X-axis is given by
y² = 4a(x + a) ……….(1)
Differentiating w.r.t x
2yy₁ = 4a
a = \(\frac{\mathrm{yy}_1}{2}\)
∴ From (1)
y² = 4a(x + a)
= 4 \(\frac{\mathrm{yy}_1}{2}\) (x + \(\frac{\mathrm{yy}_1}{2}\))
= 2yy₁ (x + \(\frac{\mathrm{yy}_1}{2}\))
= 2xyy₁ + y²y₁²
⇒ y = 2xy₁ + yy₁²
⇒ yy₁² + 2xy₁ – y = 0
⇒ \(y\left(\frac{d y}{d x}\right)^2+2 x\left(\frac{d y}{d x}\right)\) – y = 0
which is the required differential equation obtained on elimination of ‘a’ from (1).

Students must practice this TS Intermediate Maths 2A Solutions Chapter 10 Random Variables and Probability Distributions Ex 10(b) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2A Solutions Chapter 10 Random Variables and Probability Distributions Ex 10(b)

I.
Question 1.
In the experiment of tossing a coin n times, If the variable X denotes the number of heads and P (X = 4), P (X = 5), p (X = 6) are in arithmetic progression then find n.
Solution:
X follows binomial distribution with p = \(\frac{1}{2}\), q = \(\frac{1}{2}\)
P (X = 4), P (X = 5), P (X = 6) are in A.P.
∴ 2P (X = 5) = P (X = 4) + P (X = 6)

⇒ n² – 21n + 98 = 0
⇒ (n – 7) (n – 14) = 0
⇒ n = 7 or 14.

Question 2.
Find the minimum number of times a fair coin must be tossed so that the probability of getting atleast one head is 0.8.
Solution:
When a coin is tossed we have p = \(\frac{1}{2}\), q = \(\frac{1}{2}\)
P(X = x) = ⁿC_x p^xq^n-x
P(X = 0) = ⁿC₀ p⁰q^n-0
Given probability 0f getting atleast one head is atleast 0.8
P(X ≥ 1 ) ≥ 0.8
⇒ 1 – P (X = 0) ≥ 0.8
⇒ 1 – \(\left(\frac{1}{2}\right)^{\mathrm{n}}\) ≥ 0.8
⇒ – \(\left(\frac{1}{2}\right)^{\mathrm{n}}\) ≥ – 0.2
⇒ \(\left(\frac{1}{2}\right)^{\mathrm{n}}\) < (0.2). Which is true for n = 3.

Question 3.
The probability of a bomb hitting a bridge is 1/2 and three direct hits (not necessarily consecutive) are needed to destroy it. Find the mmiinuni number of bombs required so that the probability of bridge being destroyed is greater than 0.9.
Solution:
Given probability of a bomb hitting a bridge is \(\frac{1}{2}\).
∴ p = \(\frac{1}{2}\);
q + p = 1 ⇒ q = 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\)
Let X represents the minimum number of bombs to be dropped so that the bridge can be destroyed. Given that P (X ≥ 3) > 0.9
⇒ 1 – P(X < 3) > 0.9
⇒ 1 – [ P(X = 0) + P(X = 1) + P (X = 2)] > 0.9
⇒ 1 – [\({ }^n \mathrm{C}_0\left(\frac{1}{2}\right)^{\mathrm{n}}+{ }^{\mathrm{n}} \mathrm{C}_1\left(\frac{1}{2}\right)^{\mathrm{n}-1}\left(\frac{1}{2}\right)\) + \({ }^{\mathrm{n}} C_2\left(\frac{1}{2}\right)^{\mathrm{n}-2}\left(\frac{1}{2}\right)^2\)] > 0.9

By substituting the values for ‘n’ we see that n = 9, 10, 11. satisfies the above in equation.
∴ The minimum number of bombs to be dropped so that the bridge Is to be destroyed is n = 9.

Question 4.
If the difference between the mean and the variance of a binomial variate is 5/9 then find the probability for the event of 2 successes when the experiment is conducted 5 times.
Solution:
Given n = 5 and
given that mean – variance of a Binomial variate is \(\frac{5}{9}\).
∴ np – npq = \(\frac{5}{9}\)
np(1 – q) = \(\frac{5}{9}\)
⇒ npq = \(\frac{5}{9}\)
⇒ 5p (1 – q) = \(\frac{5}{9}\)
⇒ 5p (p) = \(\frac{5}{9}\)
⇒ p² = \(\frac{5}{9}\)
⇒ p = \(\frac{1}{3}\)
∴ q = \(\frac{2}{3}\)
∴ P(X = 2) = ⁵C₂ \(\left(\frac{1}{3}\right)^2\left(\frac{2}{3}\right)^{5-2}\)
= 10 × \(\frac{1}{9} \times \frac{8}{27}=\frac{80}{243}\)

Question 5.
One in 9 ships is likely to be wrecked, when they are set on sail. When 6 ships set on sail, find the probability for
i) Atleast one will arrive safely
ii) Exactly three will arrive safely.
Solution:
Let q = Probability of one in 9 ships to be wrecked = \(\frac{1}{9}\)
p = 1 – q
= 1 – \(\frac{1}{9}\) = \(\frac{8}{9}\)
Here n = 6.

i) Probability ¡or atleast one will arrive safely
P (X ≥ 1) = 1 – P(X = 0)
= 1 – \({ }^6 C_0\left(\frac{8}{9}\right)^0\left(\frac{1}{9}\right)^{6-0}\)
= 1 – \(\frac{1}{9^6}\)

ii) Exactly, three will arrive safely
P (X = 3) = ⁶C₃ \(\left(\frac{8}{9}\right)^3\left(\frac{1}{9}\right)^{6-3}\)
= \({ }^6 C_3 \frac{8^3}{9^3} \frac{1}{9^3}={ }^6 C_3 \frac{8^3}{9^6}\)
= \(20\left(\frac{8^3}{9^6}\right)\).

Question 6.
If the mean and variance of a binomial variate X are 2.4 and 1.44 respectively, find P (1 < X ≤ 4).
Solution:
Mean = np = 2.4;
Variance = npq = 1.44
∴ \(\frac{\mathrm{npq}}{\mathrm{np}}=\frac{1.44}{2.4}\) = 0.6
⇒ q = 0.6
and p = 1 – 0.6 = 0.4
∴ np = 2.4
⇒ n (0.4) = 2.4
⇒ n = 6
∴ P(1 < X ≤ 4) = P (X = 2) + P(X = 3) + P (X = 4)

Question 7.
If is given that 10% of the electric bulbs manufactured by a company are defective. In a sample of 20 bulbs, find the probability that more than 2 are defective.
Solution:
Probability for an electric bulb to be defective, p = \(\frac{10}{100}\) = 0.1
∴ Probability for a non defective bulb
q = 1 – p = 1 – 0.1 = 0.9
Probability to have more than 2 are defectives
⇒ P(X > 2) = 1 – P(X ≤ 2)
1 – [P (X = 0) + P(X = 1) + P(X = 2)]
We have
P(X = x) = ⁿC_x p^xq^n-x

Question 8.
On an average, rain falls on 12 days in every 30 days, find the probability that, rain will fall on just 3 days of a given week.
Solution:
Given the probability for the day to be rainy = \(\frac{12}{30}=\frac{2}{5}\)
∴ p = \(\frac{2}{5}\) and
q = 1 – p
= 1 – \(\frac{2}{5}\) = \(\frac{3}{5}\)
Also, n = 7
∴ Probability for the rain to fall on just 3 days of a given week
P(X = 3) = ⁷C₃ \(\left(\frac{2}{5}\right)^3\left(\frac{3}{5}\right)^{7-3}\)
= ⁷C₃ \(\left(\frac{2}{5}\right)^3\left(\frac{3}{5}\right)^4\)
= \(\frac{35 \times 2^3 \times 3^4}{5^7}\)

Question 9.
For a binomial distribution with mean 6 and variance 2, find the first two terms of the distribution.
Solution:
Given mean = np = 6
and variance = npq = 2
∴ q = \(\frac{\mathrm{npq}}{\mathrm{np}}=\frac{2}{6}=\frac{1}{3}\)
∴ p = 1 – q
= 1 – \(\frac{1}{3}\) = \(\frac{2}{3}\)
∴ np = 6
⇒ \(\frac{2 n}{3}\) = 6
⇒ n = 9
We have P (X = x)
= ⁿC_x p^x q^n-x

Question 10.
In a city 10 accidents take place in a span of 50 days. Assuming that the number of accidents follows the Poisson distribution, find the probability that there will be 3 or more accidents in a day.
Solution:
Here λ = \(\frac{10}{50}=\frac{1}{5}\)
∴ The probability that there will be 3 or more accidents in a day using Poisson variate.
P (X = x) = \(\frac{c^{-\lambda} \lambda^x}{x !}\)
P (X ≥ 3) = 1 – [P (X = 0) + P(X = 1) + P(X = 2)]

II.
Question 1.
Five coins are tossed 320 times. Find the frequencies of the distribution of the number of heads and tabulate the result.
Solution:
When a coin is tossed we have p = \(\frac{1}{2}\) and q = \(\frac{1}{2}\).
Here n = 5;
The frequencies of distribution of the number of heads is given using binomial distribution given by
f_x = N. ⁿC_x p^x q^n-x,
x = 0,1, 2, 3, 4, 5, (Number of heads)
when x = 0

Question 2.
Find the probability of guessing atleast 6 out of 10 of answers in
(i) True or false type examination
(ii) Multiple choice with 4 possible answers.
Solution:
i) Probability of guessing atleast 6 out of 10 answers in
(i) True or false type examination is
P(X ≥ 6) = P(X = 6) P(X = 7) + P (X = 8) + P (X = 9)
Here P (X = x) = ⁿC_x p^x q^n-x and
probability for an answer to be true or false,
p = \(\frac{1}{2}\), q = \(\frac{1}{2}\), n = 10
p – q = n = 10

ii) Probability for a question to guess in multiple choice type with 4 answers is
p = \(\frac{1}{4}\), q = \(\frac{3}{4}\)
∴ P(X ≥ 6) = P(X = 6) + P(X = 7) + P(X = 8) + P (X = 9) + P(X = 10)
where P (X = x) = ⁿC_x p^x q^n-x
= ¹⁰C_x \(\left(\frac{1}{4}\right)^x\left(\frac{3}{4}\right)^{10-x}\)

In the above two cases (i) and (ii).

i) Probability to guess 6 out of 10 questions in true or false examination is = ¹⁰C₆ \(\left(\frac{1}{2}\right)^{10}\)

ii) Probability to guess 6 out of 10 questions in Multiple choice type with 4 answers = ¹⁰C₆ . \(\frac{3^4}{4^{10}}\).

Question 3.
The number of persons joining a cinema ticket counter in a minute has poisson distribution with parameter 6. Find the probability that
(i) no one joins the queue in a particular minute
(ii) two or more persons join in the queue in a minute.
Solution:
Given λ = 6, and poisson distribution function is given by
P (X = x) = \(\frac{\lambda^x e^{-\lambda}}{x !}\), x = 0, 1, 2, 3, ………..

i) Probability that no one joins the queue in a particular minute is
P (X = 0) = \(\frac{\lambda^0 \mathrm{e}^{-6}}{0 !}\) = e^-6.

ii) Probability for two or more persons join in the queue in a minute is
P (X ≥ 2) = 1 – [P (X = 0) + P (X = 1)]
= 1 – \(\left[\mathrm{e}^{-6}+\frac{\lambda \mathrm{e}^{-\lambda}}{1 !}\right]\)
= 1 – e^-6 – 6 e^-6.

Students must practice these TS Inter 2nd Year Maths 2A Important Questions Chapter 4 Theory of Equations to help strengthen their preparations for exams.

TS Inter 2nd Year Maths 2A Theory of Equations Important Questions

Question 1.
Form the monic polynomial eduation of degree 3 whose roots are 2, 3 and 6. Given roots of required polynomial are
2, 3 and 6.
Solution:
We know that monic polynomial those roots of α, β and γ is (x -α) (x -β) (x -γ) = 0.
∴ Equation of required monk polynomial is
(x – 2)(x – 3)(x – 6) = 0
on simplification, it becomes
x³ – 11x² + 36x – 36 = 0.

Question 2.
Find the relations between the roots and the coefficients of the cubic equation
3x² – 10x² + 7x + 10 = 6.
Solution:
Given cubic equation is
3x² – 10x² + 7x + 10 = 0
On dividing the equation by ‘3’ we get,

Question 3.
Write down the relations between the roots and the coefficients of the biquadratic equation :
x⁴– 2x³ + 4x² + 6x – 21 = 0.
Solution:
Given equation is x⁴– 2x³ + 4x² + 6x – 21 = O
On comparing (1) with

Question 4.
If 1,2,3 and 4 are the roots of x⁴+ax³+bx²+ cx + d = 0, then find the values of a, b, c and d.
Solution:
Given roots of the given polynomal equation are 1, 2, 3 and 4.
∴ x⁴+ax³+bx²+ cx + d ≡ (x-1)(x-2) (x – 3) (x – 4)
= x⁴ – 10x³ 35x² – 50x + 24
On comparing coellicients of like powers of we get,
a = – 10, b = 35, c = – 50, d = 24.

Question 5.
If a,b and c are the roots of x³-px²+qx – r = 0 and r ≠0 then find \(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\) in terms of p,q,r.
Solution:
Given a ,b and c are the roots of

Question 6.
Find the sum of the squares and the sum of the cubes of the roots of the equation
x³ – px² + qx – r = 0 in terms of p, q, r.
Solution:
Let α, β and γ be roots of the given equation x³ – px² + qx – r = 0 ……………..(1)

Question 7.
Obtain the monic cubic equation, whose roots are the squares of the roots of the equation x³ + p₁x³ + p₂x + p₃ = 0.
Solution:
Let α, β and γ be the roots of the given equation x³ + p₁x³ + p₂x + p₃ = 0 ………………… (1)

Question 8.
Let α, β and γ be the roots of x³+px²+qx+r = 0. Then find
(i) Σα²
(ii) \(\Sigma \frac{1}{\alpha}\) ,If α, β,γ are non-zero
(iii) Σα³
(iv) Σβ²γ²
(v) (α+β)(β+γ)(γ+α)
Solution:
Let α, β, and γ be the roots of equation  x³+px²+qx+r = 0 ……………….(1)

Question 9.
If α, β, γ are the roots of x³ + ax² + bx + c = 0, then find ∑α²β + ∑αβ².
Solution:
Given α, β and γ  are the roots of

Question 10.
If α, β, γ are the roots of x³ + px² + qx + r = 0, then form the monic cubic equation whose rools are
α(β+ γ),β(y+α), y(α+ β).
Solution:
Given a, and y are the roots of

Question 11.
Solve x³ – 3x² – 16x + 48 = 0.
Solution:
Let f(x) = x³ – 3x² – 16x + 48
By inspection, we see that
f(3)= 27- 27 – 48+48 = 0
Hence 3 is a root of f(x) = 0
Now we divide 1(x) by (x-3), using synthetic division.

Thus the quotient is (x² – 16) and the remainder is 0.
Therefore f(x) (x – 3) (x² – 16)
= (x – 3) (x – 4) (x 4)
Hence 3, – 4, 4 are the roots of the given equation.

Question 12.
Find the roots of x⁴ – 16x³ + 86x² – 176x + 105 = 0.
Solution:
Let f(x) = x⁴ – 16x³ + 86x² – 176x + 105
By inspection we see that,
f(1)= 1- 16+86 – 176+ 105=0
Hence 1 is a root of 1(x) = 0
Now we divide f(x) by (x – 1), using synthetic division.

Therefore
x⁴ – 16x³ + 86x² – 176x + 105
(x – 1)(x³-15x² + 71x – 105) ……………… (1)
Let g(x) = x³ – 15x² + 71x – 105
By inspection g(3) = 0.
Hence 3 is a root of g(x) = 0.
Now we divide g(x) by (x -3),
using synthetic division.

Therefore g(x) (x – 3) (x² – 12x + 35) ……………. (2)
From (1) and (2),
f(x) (x – 1) (x – 3) (x² – 12x + 35)
= (x – 1) (x – 3) (x – 5) (x – 7)
Hence 1, 3, 5 and 7 are the roots of the given equation.
Now we solve equations when a relation between some of the roots is given.

Question 13.
Solve x³ – 7x² +36 = 0 given one root being twice the other.
Solution:
Let α, β, γ be the three roots of the given equation and β = 2a.
Now we have α+β+γ = 7
αβ + βγ + γα = 0
αβγ = – 36
On substituting β =2α in the above equations, we obtain
3α + γ = 7 …………………… (1)
2α²+3αγ = 0 ……………………. (2)
2α² γ = – 36 ……………………. (3)
On eliminating γ from (1) and (2), we have
2α² + 3α (7 – 3α) = 0
i.e., α² -3α = 0 or α(α -3) = 0
Therefore α = 0 or α = 3
Since α = 0 does not satisfy the given equation, we ignore this value.
Therefore α = 3 is a root of the given equation.
So, β = 6 (since β = 2α) and γ = – 2
Hence 3, 6, – 2 are the roots of the given equation.

Question 14.
Given that 2 is a root of x³ – 6x²+3x+10 = 0, find the other roots.
Solution:
Let f(x) x³ – 6x²+3x+10
Since 2 is a root of f(x) 0,
we divide f(x) by (x – 2)

Therefore
x³ – 6x² – 3x + 10 = (x – 2) (x² – 4x – 5)
= (x – 2) (x+1) (x-5)
Thus – 1, 2 and 5 are the roots of the given equation.

Question 15.
Given that two roots of 4x³ + 20x²– 23x + 6 = 0 are equal, find all the roots of the given equation.
Solution:
Let α, β, γ, and δ are the roots of
4x³ + 20x²– 23x + 6 = 0 ………………… (1)
Given that two roots of (1) are equal. Let β = α
Since α, β, γ are the roots of (1), we have

Therefore
x³ – 6x² – 3x + 10 = (x – 2) (x² – 4x – 5)
=(x – 2) (x+ 1) (x – 5)
Thus – 1, 2 and 5 are the roots of the given equation.
Therefore α = \(\frac{1}{2}\) or α = \(-\frac{23}{6}\)
On verification we get that α = \(\frac{1}{2}\) is a root of (1)
On substituting this value in (2), we get γ = – 6
Therefore \(\frac{1}{2}, \frac{1}{2},-6\) are the roots of (1).

Question 16.
Given that the sum of two roots of x⁴ – 2x³+ 4x² + 6x – 21 = 0 is zero. Find the roots of the equation.
Solution:
Let α, β, γ, and δ be the roots of (1), and α + β = 0 ……………. (1)
From the relation between the coefficients and the roots, we have
α + β + γ +δ = 2 so γ + δ = 2 ……………… (2)
Therefore the quadratic equation having roots α and β is x² – 0, x + αβ=0
The quadratic equation having roots γ + δ is x²-2x +q =0

Question 17.
Solve 4x³ – 24x²+ 23x+ 18=0 given that the roots of this equation are in arithmetic progression.
Solution:
Let a – d, a, a + d be the roots of the given equation. These are in A.P. From the relation between the coefficients and the roots, we have

Question 18.
Solve x³-7x²+14x-8=0 given that the roots are in geometric progression.
Solution:

Hence the roots of the given equation are 1, 2 and 4.

Question 19.
Solve x⁴-5x³+5x²+ 5x – 6 = 0 given that the product of two of its roots is 3.
Solution:
Let α , β, γ be the roots of the given equation.

we get γ = 3 and δ = 1 or γ = 1 and δ = 3
Hence the roots of the given equation are 2,- 1, 3 and 1.

Question 20.
Solve x⁴+4x³– 2x⁴– 12x+ 9 = 0 given that it has two pairs of equal roots.
Solution:
Let the roots of the given equation be

Therefore 1, 1, -3, -3 are the roots of the given equation.

Question 21.
Prove that the sum of any two of the roots of the equation x⁴ +px³ + qx² + rx + s = 0 is equal to the sum of the remaining two roots of the equation if p³ – 4pq + Sr = 0.
Solution:
Suppose that the sum of two of the roots of the given equation is equal to the sum of the remaining two roots.
Let α, β, γ, δ be roots of the given equation such that α + β = γ + δ


Take \(b=\frac{p}{2}\)
Then equations (1), (2) and (4) are satisfied.
In view of (5), equation (3) is also satisfied.
Hence (x² + bx + c) (x² + bx + d)
=x⁴+ 2bx³+(b²+c+d)x²+h(c +d)x+cd
= x⁴ +px³ +qx² +rx+s
Hence the roots of the given equation are α₁, β₁,γ₁ and δ₁, where α₁ and β₁ are the roots of the equations
x² + bx + c = 0 and γ₁ and δ₁ are those of the equation x² + bx+ d = 0
We have α₁ + β₁ = -b = γ₁ + δ₁

Question 22.
Form the monic polynomial equation of degree 4 whose roots are \(4+\sqrt{3}, 4-\sqrt{3}\)
Solution:
The required equation is
\(\{\mathrm{x}-(4+\sqrt{3})\}\{\mathrm{x}-(4-\sqrt{3})\}\)
{x – (2+i)} {x – (2 – i)) =0
i.e., (x² – 8x + 13) (x² – 4x + 5) = 0
i.e., x² – 12x³ + 50x – 92x + 65 = 0

Question 23.
Solve 6x⁴ -13x² – 35x² – x+3 = 0 given that one of its roots is \(2+\sqrt{3}\)
Solution:
Since \(2+\sqrt{3}\) is a root of the giver equation, by Theorem 4.3.9, \(2+\sqrt{3}\) is also a root of it. The quadratic factor corresponding to these two roots is x² – 4x + 1.
On dividing 6x⁴ -13x¹ – 35x² –  x + 3 by x² – 4x + 1 (by synthetic division) weet the quotient 6x² + 11x + 3.
Therefore 6x – 13x³ – 35x² – x + 3 =(x²– 4x+ 1) (6x²+ 11x+3)
Hence the other roots are obtained from 6x² + 11x + 3 = 0
On solving this equation, we get
\(\mathrm{x}=-\frac{1}{3} \text { or }-\frac{3}{2}\)
Thus the roots of the given equation are
\(-\frac{1}{3},-\frac{3}{2}, 2 \pm \sqrt{3}\)

Question 24.
Find the polynomial equation of degree 4 whose roots are the negatives of the roots
of x⁴ – 6x³ +7x² – 2x + 1 = 0.
Solution:
Let f(x) = x⁴ – 6x³ +7x² – 2x + 1
By Theorem 4.4.1, the equation (- x) = 0 has the desired property.
We have
f(-x) = (-x)⁴ – 6(-x)³. 7(-x)² – 2(-x) + 1
= x⁴+6x³+7x²+2x+ 1
Hence x⁴ – 6x³ +7x² – 2x + 1 + 6x³ + 7x² + 2x+ 1 = 0 is the desired equation.

Question 25.
Find an algebraic equation of degree 4 whose roots are 3 times the roots of equation 6x⁴ – 7x³ + 8x² – 7x + 2 = 0.
Solution:
Let f(x) = 6x⁴ – 7x³ + 8x² – 7x + 2
By Theorem 4.4.3, the equation
\(f\left(\frac{x}{3}\right)=0\) has the desired properties. We have

Hence 6x⁴– 21x³+72x²-189x +162 = 0 is the desired equation.

Question 26.
Form the equation whose roots are m times the roots of the equation
\(x^3+\frac{1}{4} x^2-\frac{1}{16} x+\frac{1}{72}=0\) and deduce the case when m = 12.
Solution:
From the note 4.4.2 and note 4.4.4., it follows that

is a polynomial equation of degree 3, whose roots are m times those of the given equation. On taking m = 12, equation (1) reduces to

Question 27.
Find the polynomial equation of degree 5 whose roots are the translates of the roots of x⁵+4x³ -x²+11 = 0 by – 3.
Solution:
By Theorem 4.4.6, the equation
(x+3)⁵+4(x+3)³_(x+3)² +11 = 0 has the desired properties.
On simplifying the above equation, we get
x⁵ + 15x⁴ + 94x³ + 305x² + 507x + 353 = 0.
The transformed equation can also be object by synthetic division
Let f(x) =x⁵+4x³-x²+ 11
Suppose that f(x + 3) A₀x⁵ + A₁x⁴ + A₂x³ + A₃x² + A₄x + A₅
Then by note 4.4.8, the coefficients
A₀, A₁ , …………………………. A₅ can be obtained as follows

Therefore the roots of the equation
x⁵ + 15x⁴ + 94x³ + 305x² + 507x + 353 = 0 are the translates of the roots of the given equation by – 3.

Question 28.
Find the algebraic equation of degree 4 whose roots are the translates of the roots of 4x⁴ + 32x³ + 83x² + 76x + 21 = O by 2.
Solution:
By Theorem 4.4.6, the equation
4 (x – 2)⁴ + 32 (x – 2)³ + 83 (x – 2)⁴+76(x-2) + 21 =0 has desired properties.
On simplifying the above equation, we get 4x⁴– 13x²+90
Other mehod: The equation A₀x⁴ . A₁x³ +………… + A₄ = 0 whose coefficients are obtained by synthetic division as given below, has the desired properties

Hence the equation 4x⁴ – 13x² + 9 = 0 has the desired properties.

Question 29.
Find the polynomial equation whose roots are the reciprocals of the roots of the equation x⁴ + 3x³ – 6x² + 2x – 4 = 0.
Solution:
Let f(x) = x⁴ + 3x³ – 6x² + 2x – 4
By theorem 4.4.9, the equation
\(x^4 f\left(\frac{1}{x}\right)=0\) has the desired properties.
Therefore
\(x^4\left[\frac{1}{x^4}+3 \frac{1}{x^3}-6 \frac{1}{x^2}+\frac{2}{x}-4\right]=0\)
i.e., 4x⁴ – 2x³ + 6x² – 3x – 1 = 0 is the required equation.

Question 30.
Find the polynomial equation whose roots are the squares of the roots of x³– x² + 8x – 6 = 0.
Solution:
Let f(x) = x³– x² + 8x – 6 = 0.
Then as per the notation introduced in Note 4.413, we have

The equation x³+ 15x² + 52x -36 = 0 has the desired properties.

Question 31.
Show that 2x³+5x²+5x+2=0 is are reciprocal equation of class one.
Solution:
Let f(x) = 2x³+5x²+5x+2=0
Then 2 is the leading coefficient.

Therefore the given equation is a reciprocal equation of class one.

Question 32.
Solve the equation 4x³ -13x² – 13x + 4 = 0.
Solution:
The given equation is an odd degree reciprocal equation of class one.
By Note 4.4.24(1), – 1 is a root of this equation.
Therefore (x + 1) is a factor of
4x³ -13x² – 13x + 4
Hence on dividing this expression by(x + 1), we get
4x³ -13x² – 13x + 4 (x + 1)(4x² – 17x+ 4)
Now the roots of the equation
4x²– 17x+4=0 are \(\frac{1}{4}\) and 4.
Therefore -1,\(\frac{1}{4}\),4 are the roots of the given equation.

Question 33.
Solve the equation
– 5x⁴ + 9x³ – 9x² + 5x – 1 = 0.
Solution:
We observe that the given equation is an odd degree reciprocal equation of class two.
By Note 4.4.24(1), 1 is a root of this equation.
Therefore (x – 1) is a factor of x⁵ – 5x⁴ + 9x³– 9x² + 5x – 1.
On dividing this expression by (x – 1), we get
x⁴ – 4x³ + 5x² – 4x + 1 as the quotient.
Now we have to solve the equation
x⁴ – 4x + 5x² – 4x + 1 = 0
On dividing this equation by x², we get
x²– 4x+5 –\(\frac{4}{x}+\frac{1}{x^2}\) = 0

Question 34.
Solve the equation 6x⁴-35x³+62x²-35x+6=0.
Solution:
We observe that the given equation is an even degree reciprocal equation of class one.
On dividing both sides of the given equation by x², we get

Then the above equation reduces to
6 (y²-2) – 35y + 62 = 0
i.e., 6y² – 35y + 50 = 0
i.e., (2y – 5) (3y – 10) = 0
Hence the roots of

Question 35.
Solve the equation
6x⁶ – 25x⁵ + 31x⁴ -31x² + 25x – 6 = 0.
Solution:
We observe that the given equation is an even degree reciprocal equation of class two. By Note 4.4.24(2), + 1 and – 1 are the roots of this equation. Hence (x + 1) and (x – 1) are the factors of the given equation.
Let f(x) = 6x⁶ – 25x⁵ + 31x⁴ -31x² + 25x – 6 = 0
On dividing this expression by (x + 1) and then by (x – 1), we get
f(x) = (x² -1) (6x⁴ – 25x³ + 37x² – 25x + 6)
Now we have to solve the equation
6x⁴ – 25x³ + 37x² -25x + 6 = 0
On dividing both sides of this equation by x², we obtain

 

Students must practice this TS Intermediate Maths 2A Solutions Chapter 9 Probability Ex 9(a) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2A Solutions Chapter 9 Probability Ex 9(a)

I.
Question 1.
In the experiment of throwing a die, consider the following events A = {1, 3, 5}, B = {2, 4, 6}, C = {1, 2, 3}. Are these events equally likely?
Solution:
If the die is thrown there is a possibility of getting 1 or 2 or 3 or 4 or 5 or 6 on any face.
Hence the events A = {1, 3, 5}, B = {2, 4, 6} and C = {1, 2, 3} are equiprobable since there is no reason to expect one in preference to others.
Hence the events A, B, C are equally likely.

Question 2.
In the experiment of throwing a die, consider the following events A = {1, 3, 5}, B = {2, 4}, C = {6} . Are these events mutually exclusive?
Solution:
The three events A, B, C are mutually exclusive since the occurrence of one of the events prevents the happening of any one of the remaining events.
Since A ∩ B ∩ C = {1, 3, 5} ∩ {2, 4} ∩ {6}
We say that the events are A, B, C are mutually exclusive.

Question 3.
In the experiment of throwing a die, consider the events A = {2, 4, 6}, B = {(3, 6}, C = {1, 5, 6}. Are these events exhaustive?
Solution:
The three events A, B, C are exhaustive if A ∪ B ∪ C = S
A ∪ B ∪ C = {2, 4, 6} ∪ {3, 6} ∪ {15 6}
= {1, 2, 3, 4, 5, 6} = S.

II.
Question 1.
Give two examples of mutually exclusive and exhaustive events.
Solution:
In tossing a coin there are two exhaustive events Head (H) and Tail (T).
In throwing a die there are six exhaustive events of getting I or 2 or 3 or 4 or 5 or 6.
In tossing a coin either heads comes up or tail but both cannot happen at the same time. These two events are mutually exclusive because happening of one event prevents the happening of the other.
In a well shuffled pack of cards if a card is drawn from 52 cards then getting an ace and getting a king are mutually exclusive events.

Question 2.
Give examples of two events that are neither mutually exclusive nor exhaustive.
Solution:
If a coin is tossed twice or two coins are tossed a time, then the events of getting head or tail are not mutually exclusive nor exhaustive.
Since we get {HH, HT, TH, TT} as events.
From a well shuffled pack of cards if two cards are drawn one after other with replacement, then getting aces on two attempts are not mutually exclusive nor exhaustive.

Question 3.
Give two examples of events that are neither equally likely nor exhaustive.
Solution:
If a die is thrown then the event of getting ‘1’ and the event of getting a prime number are neither equally likely events nor exhaustive events.
In the experiment of throwing a pair of dice then the events
E₁ = A sum 7 ( of the numbers that appear on the uppermost faces of the dice ) and
E₃ = A sum > 7 ( of the number that appear on the uppermost faces of the dice ) are neither equally likely nor mutually exclusive.

Students must practice this TS Intermediate Maths 2A Solutions Chapter 8 Measures of Dispersion Ex 8(a) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2A Solutions Chapter 8 Measures of Dispersion Ex 8(a)

I.
Question 1.
Find the mean deviation about the mean for the following data.
i) 38, 70, 48, 40, 42, 55, 63, 46, 54, 44
ii) 3, 6, 10, 4, 9, 10
Solution:
i) Mean of the given data is \(\bar{x}=\frac{38+70+48+40+42+55+63+46+54+44}{10}\)
= \(\frac{500}{10}\) = 50
The absolute values of the deviations are \(\left|x_i-\bar{x}\right|\) =12, 20, 2, 10, 8, 5, 13, 4, 4, 6
∴ Mean Deviation about the Mean = \(\frac{\sum_{\mathrm{i}=1}^{10}\left|\mathbf{x}_{\mathrm{i}}-\overline{\mathrm{x}}\right|}{n}\)
= \(\frac{12+20+2+10+8+5+13+4+4+6}{10}\)
= \(\frac{84}{10}\) = 8.4.

ii) Mean of the given data (\(\bar{x}\)) = \(\frac{\sum_{\mathbf{i}=1}^6 x_i}{n}\)
∴ \(\bar{x}\) = \(\frac{3+6+10+4+9+10}{6}=\frac{42}{6}\) = 7
The absolute values of the deviations are |x_i – \(\bar{x}\)| = 4, 1, 3, 3, 2, 3
Mean Deviation about the Mean = \(\frac{\sum_{i=1}^6\left|x_i-\bar{x}\right|}{n}\)
= \(\frac{4+1+3+3+2+3}{6}=\frac{16}{6}\) = 2.67.

Question 2.
Find the mean deviation about the median for the following data.
i) 13, 17, 16, 11, 13, 10, 16, 11, 18, 12, 17
ii) 4, 6, 9, 3, 10, 13, 2
Solution:
i) Expressing the given data in the ascending order, we get 10, 11, 11,12,13, 13, 16, 16, 17, 17, 18
Median (M) of these 11 observations is 13.
The absolute values of deviations are |x_i – M| = \(\frac{3+2+2+1+0+0+3+3+4+4+5}{11}\)
= \(\frac{27}{11}\) = 2.45.

ii) Expressing the given data in the ascending order, we get 2, 3, 4, 6, 9, 10, 13.
Median (M) of given data = 6
The absolute values of deviations are |x_i – M | = 4, 3, 2, 0, 3, 4, 7
∴ Mean Deviation about the Median = \(\frac{\sum_{\mathrm{i}=1}^7\left|\mathrm{x}_{\mathrm{i}}-\mathrm{M}\right|}{\mathrm{n}}=\frac{4+3+2+0+3+4+7}{7}\)
= \(\frac{23}{7}\) = 3.29.

Question 3.
Find the mean deviation about the mean for the following distribution.
i)

ii)
Solution:
i)

∴ Mean (\(\bar{x}\)) = \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\mathrm{N}}=\frac{534}{45}\) = 11.87

∴ Mean Deviation about the Mean = \(\frac{\sum_{i=1}^4 f_i\left|x_i-\bar{x}\right|}{N}=\frac{31.95}{45}\) = 0.71.

ii)

∴ Mean (\(\bar{x}\)) = \(\frac{\sum \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\mathrm{N}}=\frac{4000}{80}\) = 50

∴ Mean Deviation about the Mean = \(\frac{\sum_{i=1}^5 f_i\left|x_i-\bar{x}\right|}{N}=\frac{1280}{80}\) = 16.

Question 4.
Find the mean deviation about the median for the following frequency distribution.

Solution:

Hence N = 26 and \(\frac{N}{2}\) = 13
Median (M) = 7
Median Deviation about Median = \(\frac{\sum_{\mathrm{i}=1}^6 \mathrm{f}_{\mathrm{i}}\left|\mathrm{x}_{\mathrm{i}}-\mathrm{M}\right|}{\mathrm{N}}=\frac{84}{26}\) = 3023.

Note:
We shall identify the observation whose cumulative frequency is equal to or just greater than N/2. This is the median of the data. Here median is “7”.

II.
Question 1.
Find the mean deviation about the median for the following continuous distribution.
i)

ii)
Solution:

i)

Hence L = 20, \(\frac{N}{2}\) = 25, f₁ = 14, f = 14, h = 10
Median (M) = L + \(\left[\frac{\left[\frac{\mathrm{N}}{2}-\mathrm{f}_1\right]}{\mathrm{f}}\right]\) h
= 20 + \(\frac{25-14}{14}\) × 10
= 20 + \(\frac{110}{14}\)
= 20 + 7.86 = 27.86.
∴ Mean Deviation about Median = \(\frac{\sum_{\mathrm{i}=1}^6 \mathrm{t}_{\mathrm{i}}\left|\mathrm{x}_{\mathrm{i}}-\mathrm{M}\right|}{\mathrm{N}}\)
= \(\frac{517.16}{50}\) = 10.34.

ii)

Here N = 100, \(\frac{N}{2}\) = 50, L = 40, f₁ = 32, f = 28, h = 10
Median (M) = L + \(\left\{\frac{\left[\frac{\mathrm{N}}{2}-\mathrm{f}_1\right]}{\mathrm{f}}\right\}\) h
= 40 + \(\frac{50-32}{28}\) × 10
= 40 + \(\frac{180}{28}\)
= 40 + 6.43 = 46.43.
∴ Mean Deviation about Median = \(\frac{\sum_{i=1}^8 f_i\left|x_i-M\right|}{N}=\frac{1428.6}{100}\) = 14.29.

Question 2.
Find the mean deviation about the mean for the following continuous distribution.

Solution:

Mean (\(\bar{x}\)) = A + \(\frac{\Sigma f_i \mathrm{~d}_{\mathrm{i}}}{\mathrm{N}}\) . h
= 130 + \(\left(\frac{-47}{100}\right)\) . 10
= 130 – 1.7 = 125.3.

∴ Mean Deviation about Mean = \(\frac{\sum_{i=1}^6 f_i\left|x_i-\bar{x}\right|}{N}\)
= \(\frac{1128.8}{100}\) = 11.29.

Question 3.
Find the variance for the discrete data given below.
i) 6, 7, 10, 12, 13, 4, 8, 12
ii) 350, 361, 370, 373, 376, 379, 385, 387, 394, 395.
Solution:
i) Mean (\(\bar{x}\)) = \(\frac{6+7+10+12+13+4+8+12}{8}=\frac{72}{8}\) = 9

Variance (σ²) = \(\frac{\sum_{\mathrm{i}=1}^8\left(x_i-\bar{x}\right)^2}{n}=\frac{74}{8}\) = 9.25.

ii)

Mean (\(\bar{x}\)) = \(\frac{350+361+370+373+376+379+385+387+394+395}{10}\)
= \(\frac{3770}{10}\) = 377.
Variance (σ²) = \(\frac{\sum_{i=1}^{10}\left(x_i-\bar{x}\right)^2}{n}=\frac{1832}{10}\) = 183.2.

Question 4.
Find the variance and standard deviation of the following frequency distribution.

Solution:

Mean (x) = \(\frac{760}{40}\) = 19
Variance (σ²) = \(\frac{\Sigma \mathrm{f}_{\mathrm{i}}\left(\mathrm{x}_{\mathrm{i}}-\overline{\mathrm{x}}\right)^2}{\mathrm{~N}}=\frac{1736}{40}\) = 43.4
Standard Deviation (σ) = \(\sqrt{43.4}\) = 6.59.

III.
Question 1.
Find the mean and variance using the step deviation method, of the following tabular data, giving the age distribution of 542 members.

Solution:

Question 2.
The coefficent of variation of two distributions are 60 and 70 and their standard deviations are 21 and 16 respectively. Find their arithmetic means.
Solution:
C.V = \(\frac{\sigma}{\overline{\bar{X}}}\) × 100

i) 60 = \(\frac{21}{\overline{\mathrm{X}}}\) × 100
\(\overline{\mathrm{X}}\) = \(\frac{21 \times 100}{60}\) = 35

ii) 70 = \(\frac{16}{\overline{\mathrm{Y}}}\) × 100
\(\overline{\mathrm{Y}}\) = \(\frac{16 \times 100}{70}\) = 22.857.

Question 3.
From the prices of shares X and Y given below, for 10 days of trading, find out which share is more stable?

Solution:
Variance is independent ol change of origin.

V(X) = \(\frac{\Sigma x_i^2}{n}-(\bar{x})^2\)
= \(\frac{360}{10}-\left(\frac{10}{10}\right)^2\)
= 36 – 1 = 35.

V(Y) = \(\frac{\Sigma Y_i^2}{n}-(\bar{Y})^2\)
= \(\frac{290}{10}-\left(\frac{50}{10}\right)^2\)
= 29 – 25 = 4.

Question 4.
The mean of 5 observations is 4.4. Their variance is 8.24. If three of the observations are 1, 2 and 6. Find the other
two observations.
Solution:

S.D = \(\sqrt{\frac{\Sigma \mathrm{m}^2}{\mathrm{n}}-(\overline{\mathrm{x}})^2}\)
\(\bar{x}\) = 4.4
⇒ 4.4 = \(\frac{1+2+6+x+y}{5}\)
⇒ 9 + x + y = 22
⇒ x + y = 13 …………..(1)
S.D² = \(\frac{1+4+36+x^2+y^2}{5}\) – (4.4)²
= \(\frac{41+x^2+y^2}{5}\) – 19.36
S.D² = Variance
Variance = \(\frac{41+x^2+y^2}{5}\) – 19.36
8.24 + 19.36 = \(\frac{41+x^2+y^2}{5}\)
41 + x² + y² = 5×27.6
x² + y² = 138 – 41
x² + y² = 97 …………..(2)
From (1) and (2),
x² + (13 – x)² = 97
x² + 169 + x² – 26x = 97
2x² – 26x + 72 = 0
x² – 13x + 36 = 0
x² – 9x – 4x + 36 = 0
x (x – 9) – 4 (x – 9) = 0
(x – 9) (x – 4) = 0
x = 4, 9
Put x = 4 in (1)
y = 13 – 4= 9
Put x = 9 in (1)
y = 13 – 9 = 4
∴ If x = 4, then y = 9.
If x = 9, then y = 4.

Question 5.
The arithmetic mean and standard deviation of a set of 9 items are 43 and 5 respectively. If an item of value 63 is added to that set, find the new mean and standard deviation of 10 items set given.
Solution:

Students must practice these TS Inter 2nd Year Maths 2A Important Questions Chapter 2 De Moivre’s Theorem to help strengthen their preparations for exams.

TS Inter 2nd Year Maths 2A De Moivre’s Theorem Important Questions

Question 1.
Simplify \(\frac{(\cos \alpha+i \sin \alpha)^4}{(\sin \beta+i \cos \beta)^8}\)
Solution:

Question 2.
If m,n are integers and x = cos α + i sin α, y = cos β + i sin β then prove that
x^m yⁿ + \(\frac{1}{x^m y^n}\) = cos (mα +nβ) and
x^m yⁿ – \(\frac{1}{x^m y^n}\) = 2i sin (mα +nβ)
Solution:

Question 3.
If n is a positive Integer, show that \((1+i)^n+(1-i)^n=2^{\frac{n+2}{2}} \cos \left(\frac{n \pi}{4}\right)\)
Solution:

Question 4.
If n is an Integer then show that
(1 + cos θ + i sin θ)ⁿ + (1 + cos θ – i sin θ)ⁿ \(=2^{n+1} \cos ^n\left(\frac{\theta}{2}\right) \cos \left(\frac{n \theta}{2}\right)\)
Solution:
L.H.S
(1 + cos θ + i sin θ)ⁿ + (1 + cos θ – i sin θ)ⁿ

Question 5.
If cos α+cos β + cos γ = 0 = sin α + sin β + sin γ, Prove that cos² α +cos² β +cos γ = \(\frac{3}{2}\) sin² α + sin² β + sin² γ.
Solution:

Question 6.
Find all the values of \((\sqrt{3}+i)^{1 / 4}\)
Solution:
The modulus amplitude form of

Question 7.
Find all the roots of the equation
x¹¹ – x⁷ + x⁴ -1 = 0
Solution:
x¹¹ – x⁷ + x⁴ -1  = x⁷(x⁴-1) +1 (x⁴– 1) = (x⁴-1)(x⁷. 1)
Therefore the roots of the given equations are precisely the roots of unity and 7th roots of – 1.
They are cis = \(\frac{2 \mathrm{k} \pi}{4} \) = cis \(\frac{\mathrm{k} \pi}{4}\) k∈{0,1,2,3} and

Question 8.
If 1, ω, ω² are the cube roots of unity, prove that

Solution:

Question 9.
If α, β are the roots of the equation x² + x + 1 = 0 then prove that α⁴ + β⁴ + α^-1 = β^-1
Solution:
Since α, β are the complex cube roots of unity,
we may take α = ω, β = ω²

Students must practice this TS Intermediate Maths 2A Solutions Chapter 7 Partial Fractions Ex 7(a) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2A Solutions Chapter 7 Partial Fractions Ex 7(a)

Resolve the following fractions into partial fractions.

I.
Question 1.
\(\frac{2 x+3}{(x+1)(x-3)}\)
Solution:
Let \(\frac{2 x+3}{(x+1)(x-3)}=\frac{A}{x+1}+\frac{B}{x-3}\)
⇒ A (x – 3) + B (x + 1) = 2x – 3 …………..(1)
Substituting x = 3 in (1),
weget 4B = 9 .
⇒ B = \(\frac{9}{4}\)
Substituting x = – 1 in (1),
we get – 4A = 1
⇒ A = \(\frac{-1}{4}\)
∴ \(\frac{2 x+3}{(x+1)(x-3)}=\frac{9}{4(x-3)}-\frac{1}{4(x+1)}\).

Question 2.
\(\frac{5 x+6}{(2+x)(1-x)}\)
Solution:
Let \(\frac{5 x+6}{(2+x)(1-x)}=\frac{A}{2+x}+\frac{B}{1-x}\)
⇒ A (1 – x) + B (2 + x) = 5x + 6 ……………..(1)
Substituting x = 1 in (I),
weget 3B = 11
⇒ B = \(\frac{11}{3}\)
Substituting x = – 2 in (1),
we get 3A = – 4
⇒ A = \(\frac{-4}{3}\)
∴ \(\frac{5 x+6}{(2+x)(1-x)}=\frac{11}{3(1-x)}-\frac{4}{3(2+x)}\).

II.
Question 1.
\(\frac{3 x+7}{x^2-3 x+2}\)
Solution:
We know that
\(\frac{3 x+7}{x^2-3 x+2}=\frac{3 x+7}{(x-2)(x-1)}\)
Let \(\frac{3 x+7}{(x-2)(x-1)}=\frac{A}{x-2}+\frac{B}{x-1}\)
⇒ A (x – 1) + B(x – 2) = 3x + 7 …………..(1)
SubstitutIng x = 2 in (1)
we get A = 13
Substituting x = 1 in (1)
we get – B = 10 i.e., B = – 10
∴ \(\frac{3 x+7}{x^2-3 x+2}=\frac{13}{x-2}-\frac{10}{x-1}\)

Question 2.
\(\frac{x+4}{\left(x^2-4\right)(x+1)}\)
Solution:
We know that
\(\frac{x+4}{\left(x^2-4\right)(x+1)}=\frac{x+4}{(x-2)(x+2)(x+1)}\)
Let \(\frac{x+4}{(x-2)(x+2)(x+1)}\) = \(\frac{A}{x-2}+\frac{B}{x+2}+\frac{C}{x+1}\)
A (x + 2) (x + 1) + B (x – 2) (x + 1) + C (x – 2) (x + 2) = x + 4 …………..(1)
Substituting x = 2 in (1), we have
12A = 6
A = \(\frac{1}{2}\)
Substituting x = – 2 in (1), we have
4B = 2
⇒ B = \(\frac{1}{2}\)
Substituting x = – 1 in (1), we have
– 3C = 3
⇒ C = – 1
∴ \(\frac{x+4}{\left(x^2-4\right)(x+1)}\) = \(\frac{1}{2(x-2)}+\frac{1}{2(x+2)}-\frac{1}{x+1}\)

Question 3.
\(\frac{2 x^2+2 x+1}{x^3+x^2}\)
Solution:
We know that
\(\frac{2 x^2+2 x+1}{x^3+x^2}=\frac{2 x^2+2 x+1}{x^2(x+1)}\)
Let \(\frac{2 x^2+2 x+1}{x^2(x+1)}=\frac{A}{x}+\frac{B}{x^2}+\frac{C}{x+1}\)
⇒ Ax (x + 1) + B (x + 1) + Cx2 = 2x + 2x + 1
Substituting x = 0 in (1), we have B = 1
Substituting x = – 1 in (1), we have C = 1
Equating coefficient of x² on both sides in (1), we have
A + C = 2
⇒ A = 1
∴ \(\frac{2 x^2+2 x+1}{x^3+x^2}=\frac{1}{x}+\frac{1}{x^2}+\frac{1}{x+1}\).

Question 4.
\(\frac{2 x+3}{(x-1)^3}\)
Solution:
Let \(\frac{2 x+3}{(x-1)^3}\) = \(\frac{A}{x-1}+\frac{B}{(x-1)^2}+\frac{C}{(x-1)^3}\)
⇒ A(x – 1)² + B(x – 1) + C = 2x + 3 ……………..(1)
Substituting x = 1 in (1).
we get C = 5
Equating coefficient of x² on both sides in (1)
We get A = 0
Equating coefficient of x on both sides in (1)
We get – 2A + B = 2
⇒ B = 2.

Alternate method:
Let x – 1 = y

Question 5.
\(\frac{x^2-2 x+6}{(x-2)^3}\)
Solution:
Let x – 2 = y

III.
Question 1.
\(\frac{x^2-x+1}{(x+1)(x-1)^2}\)
Solution:
Let \(\frac{x^2-x+1}{(x+1)(x-1)^2}\) = \(\frac{A}{x+1}+\frac{B}{x-1}+\frac{C}{(x-1)^2}\)
A (x – 1)² + B (x + 1) (x – 1) + C (x + 1) = x² – x + 1 ………..(1)
Substituting x = 1 in (1), we get
2C = 1
⇒ C = \(\frac{1}{2}\)
Substituting x = – 1 in (1), we get
4A = 3
⇒ A = \(\frac{3}{4}\)
Equating coefficient of x² on both sides in (1)
We get A + B = 1
\(\frac{3}{4}\) + B = 1
⇒ B = \(\frac{1}{4}\)
∴ \(\frac{x^2-x+1}{(x+1)(x-1)^2}\) = \(\frac{3}{4(x+1)}+\frac{1}{4(x-1)}+\frac{1}{2(x-1)^2}\)

Question 2.
\(\frac{9}{(x-1)(x+2)^2}\)
Solution:
Let \(\frac{9}{(x-1)(x+2)^2}\) = \(\frac{A}{x-1}+\frac{B}{x+2}+\frac{C}{(x+2)^2}\)
⇒ A (x + 2)² + B (x – 1) (x + 2) + C (x – 1) = 9 …………….(1)
Substituting x = 1 in (1), we get
9A = 9
⇒ A = 1
Substituting x = – 2 in (1), we get
– 3C = 9
⇒ C = – 3
Equating coefficient of x² on both sides in (1),
we get A + B = 0
⇒ B = – 1
∴ \(\frac{9}{(x-1)(x+2)^2}\) = \(\frac{1}{x-1}-\frac{1}{(x+2)}-\frac{3}{(x+2)^2}\).

Question 3.
\(\frac{1}{(1-2 x)^2(1-3 x)}\)
Solution:
Let \(\frac{1}{(1-2 x)^2(1-3 x)}\) = \(\frac{A}{(1-3 x)}+\frac{B}{(1-2 x)}+\frac{C}{(1-2 x)^2}\)
⇒ A (1 – 2x)² + B (1 – 3x) (1 – 2x) + C (1 – 3x) = 1 …………..(1)
Substituting x = \(\frac{1}{2}\) in (1),
we get \(\frac{-C}{2}\) = 1
⇒ C = – 2
Substituting x = \(\frac{1}{3}\) in (1),
we get \(\frac{\mathrm{A}}{9}\) = 1
⇒ A = 9
Substituting x = 0 in (1),
We get A + B + C = 1
⇒ 9 + B – 2 = 1
⇒ B = – 6
∴ \(\frac{1}{(1-2 x)^2(1-3 x)}\) = \(\frac{9}{1-3 x}-\frac{6}{1-2 x}-\frac{2}{(1-2 x)^2}\)

Question 4.
\(\frac{1}{x^3(x+a)}\)
Sol.
Let \(\frac{1}{x^3(x+a)}=\frac{A}{x+a}+\frac{B}{x}+\frac{C}{x^2}+\frac{D}{x^3}\)
⇒ Ax³ + Bx² (x + a) + Cx (x + a) + D (x + a) = 1 …………(1)
Substituting x = – a in (1),
we get – a³A = 1
⇒ A = \(\frac{-1}{a^3}\)
Equating coefficient of x³ on both sides,
we get A + B = 0
⇒ B = \(\frac{-1}{a^3}\)
Substituting x = 0 in (1),
we get aD = 1
Equating coefficient of x on both sides,
we get aC + D = 0
⇒ aC + \(\frac{1}{a}\) = 0
⇒ C = \(\frac{-1}{a^2}\)
∴ \(\frac{1}{x^3(x+a)}\) = \(\frac{-1}{a^3(x+a)}+\frac{1}{a^3 x}-\frac{1}{a^2 x^2}+\frac{1}{a x^3}\).

Question 5.
\(\frac{x^2+5 x+7}{(x-3)^3}\)
Solution:
Let x – 3 = y

Question 6.
\(\frac{3 x^3-8 x^2+10}{(x-1)^4}\)
Solution:
Let x – 1 = y

Students must practice this TS Intermediate Maths 2A Solutions Chapter 7 Partial Fractions Ex 7(d) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2A Solutions Chapter 7 Partial Fractions Ex 7(d)

Question 1.
Find the coefficietil of x³ in the power series expansion of \(\frac{5 x+6}{(x+2)(1-x)}\) specifying the region in which the expansion is valid.
Solution:
Given rational fraction \(\frac{5 x+6}{(x+2)(1-x)}\)
Let \(\frac{5 x+6}{(x+2)(1-x)}\) = \(\frac{A}{x+2}+\frac{B}{1-x}\)
⇒ A (1 – x) + B (x + 2) = 5x + 6 …………..(1)
Substituting x = 1 in (1), we get
3B = 11
⇒ B = \(\frac{11}{3}\)
Substituting x = – 2 in (1), we get
3A = – 4
⇒ A = \(\frac{-4}{3}\)

Question 2.
Find the coefficient of x⁴ in the power series expansion of \(\frac{3 x^2+2 x}{\left(x^2+2\right)(x-3)}\) specifying the Interval in which the expansion is valid.
Solution:
Let \(\frac{3 x^2+2 x}{\left(x^2+2\right)(x-3)}=\frac{A}{x-3}+\frac{B x+C}{x^2+2}\)
⇒ A (x² + 2) + (Bx + C) (x – 3) = 3x² + 2x ……………(1)
Substituting x = 3 ¡n (1), we get
11A = 33
⇒ A = 3
Equating coefficient of x² on both sides in (1), we get
A + B = 3
⇒ 3 + B = 3
⇒ B = 0
Substituting x = 0 in (1), we get
2A – 3C = 0
⇒ 3C = 2A
⇒ C = 2

The above expansions are valid for |x| < √2.

Question 3.
Find the coefficient of xⁿ in the power series expansion of \(\frac{x-4}{x^2-5 x+6}\) specifying the region in which the expansion is valid.
Solution:
We know that
\(\frac{x-4}{\left(x^2-5 x+6\right)}=\frac{x-4}{(x-2)(x-3)}\)
Let \(\frac{x-4}{x^2-5 x+6}=\frac{A}{(x-2)}+\frac{B}{(x-3)}\)
⇒ A(x – 3) + B(x – 2) = x – 4 …………(1)
Substituting x = 3 in (1), we get B = – 1
substituting x = 2 in (1), we get A = 2

Question 4.
Find the coefficient of xⁿ in the power series expansion of \(\frac{3 x}{(x-1)(x-2)^2}\)
Solution:
Let \(\frac{3 x}{(x-1)(x-2)^2}\) = \(\frac{A}{x-1}+\frac{B}{x-2}+\frac{C}{(x-2)^2}\)
A (x – 2)² + B (x – 1) (x – 2) + C (x – 1) = 3x
Substituting x = 1 in (1), we get A = 3
Substituting x = 2 in (2), we get C = 6
Equating coefficient of x² in (1) we get
A + B = 0
⇒ B = – A
⇒ B = – 3
∴ \(\frac{3 x}{(x-1)(x-2)^2}\) = \(\frac{3}{x-1}-\frac{3}{x-2}+\frac{6}{(x-2)^2}\)
= – 3 (1 – x)^-1 + \(\frac{3}{2}\left(1-\frac{x}{2}\right)^{-1}+\frac{3}{2}\left(1-\frac{x}{2}\right)^{-2}\)
Now
(1 – x)^-1 = 1 + x + x² + …………. + xⁿ + ……….., if |x| < 1

Students must practice this TS Intermediate Maths 2A Solutions Chapter 7 Partial Fractions Ex 7(c) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2A Solutions Chapter 7 Partial Fractions Ex 7(c)

Resolve the following fractions into partial fractions.

Question 1.
\(\frac{x^2}{(x-1)(x-2)}\)
Solution:
The given rational fraction \(\frac{x^2}{(x-1)(x-2)}\) is improper with degree of numerater is equal
to degree of denominator.
∴ \(\frac{x^2}{(x-1)(x-2)}\) = 1 + \(\frac{r(x)}{(x-1)(x-2)}\)
Let \(\frac{x^2}{(x-1)(x-2)}\) = 1 + \(\frac{A}{x-1}+\frac{B}{x-2}\)
⇒ (x – 1) (x – 2) + A (x – 2) + B (x – 1) = x² …………..(1)
Substituting x = 1 in (1), we get
– A = 1
⇒ A = – 1
Substituting x = 2 in (1), we get
B = 4
∴ \(\frac{x^2}{(x-1)(x-2)}\) = 1 – \(\frac{1}{x-1}+\frac{4}{x-2}\).

Question 2.
\(\frac{x^3}{(x-1)(x+2)}\)
Solution:
The given rational fraction \(\frac{x^3}{(x-1)(x+2)}\) is improper with degree of numerator is greater than degree of denominator.
Clearly
\(\frac{x^3}{(x-1)(x+2)}\) = (x – 1) + \(\frac{3 x-2}{(x-1)(x+2)}\)
Let \(\frac{3 x-2}{(x-1)(x+2)}\) = \(\frac{A}{(x-1)}+\frac{B}{x+2}\)
⇒ A (x + 2) + B(x – 1) = 3x – 2 …………..(1)
Substituting x = 1 in (1), we get
3A = 1
⇒ A = \(\frac{1}{3}\)
Substituting x = – 2 in (1), we get
– 3B = – 8
⇒ B = \(\frac{8}{3}\)
∴ \(\frac{x^3}{(x-1)(x+2)}\) = x – 1 + \(\frac{1}{3(x-1)}+\frac{8}{3(x+2)}\).

Question 3.
\(\frac{x^3}{(2 x-1)(x-1)^2}\)
Solution:
The given rational fraction \(\frac{x^3}{(2 x-1)(x-1)^2}\) is improper as degree of numerator is equal to degree of denominator.
Clearly \(\frac{x^3}{(2 x-1)(x-1)^2}=\frac{1}{2}+\frac{r(x)}{(2 x-1)(x-1)^2}\)
Let \(\frac{x^3}{(2 x-1)(x-1)^2}\) = \(\frac{1}{2}\) + \(\frac{A}{(2 x-1)}+\frac{B}{(x-1)}+\frac{C}{(x-1)^2}\)
⇒ (2x – 1) (x – 1)² + 2A (x – 1)² + 2B (2x – 1)(x – 1) + 2C (2x – 1) = 2x³ ………..(1)
Substituting x = 1 in (1), we get C = 1
Substituting x = \(\frac{1}{2}\) in (1), we get
\(\frac{\mathrm{A}}{2}=\frac{1}{4}\)
⇒ A = \(\frac{1}{2}\)
Substituting x = 0 in (I), we get
– 1 + 2A + 2B – C = 0
⇒ – 1 + 1 + 2B – 2 = 0
⇒ B = 1
∴ \(\frac{x^3}{(2 x-1)(x-1)^2}\) = \(\frac{1}{2}+\frac{1}{2(2 x-1)}+\frac{1}{x-1}+\frac{1}{(x-1)^2}\).

Question 4.
\(\frac{x^3}{(x-a)(x-b)(x-c)}\)
Solution:
The given rational fraction \(\frac{x^3}{(x-a)(x-b)(x-c)}\) is improper as degree of numerator is equal to degree of denominator.
Let \(\frac{x^3}{(x-a)(x-b)(x-c)}\) = 1 + \(\frac{A}{x-a}+\frac{B}{x-b}+\frac{C}{x-c}\)
⇒ (x – a) (x – b) (x – c) + A (x – b) (x – c) + B (x – a) (x – c) + C (x – a) (x – b) = x³ ………..(1)
Substituting x = a in (1), we get,
A (a – b) (a – c) = a³
⇒ A = \(\frac{a^3}{(a-b)(a-c)}\)
Substituting x = b in (1), we get.
B = \(\frac{b^3}{(b-c)(b-a)}\)
Substituting x= c in (1), we get

Students must practice this TS Intermediate Maths 2A Solutions Chapter 6 Binomial Theorem Ex 6(c) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2A Solutions Chapter 6 Binomial Theorem Ex 6(c)

I.
Question 1.
Find an approximate value of the following corrected to 4 decimal places.
i) \(\sqrt[5]{242}\)
ii) \(\sqrt[7]{127}\)
iii) \(\sqrt[5]{32.16}\)
iv) \(\sqrt{199}\)
v) \(\sqrt[3]{1002}-\sqrt[3]{998}\)
vi) \((1.02)^{3 / 2}-(0.98)^{3 / 2}\)
Solution:
i) \(\sqrt[5]{242}\) = (243 – 1)^{\(\frac{1}{5}\)}
= (243)^{\(\frac{1}{5}\)} (1 – \(\frac{1}{243}\))^{\(\frac{1}{5}\)}
= 3 \(\left[1-\frac{1}{5} \cdot \frac{1}{24.3}+\frac{\frac{1}{5}\left(\frac{1}{5}-1\right)}{2 !}\left(\frac{1}{243}\right)^2-\ldots .\right]\)
= 3 [1 – 0.000823 + ……………]
= 3 (0.999177)
⇒ \(\sqrt[5]{242}\) = 2.997531.

ii) \(\sqrt[7]{127}\)

= 2 (1 – 0.0011161 + ……………)
= 2 (0.99888) = 1.9977.

iii) \(\sqrt[5]{32.16}\)

iv) \(\sqrt{199}\)
= (196 + 3)^1/2
= (196)^1/2 (1 + \(\frac{3}{196}\))^1/2
= 14 (1 + 0.0153)^1/2
= 14 [1 + \(\frac{0.0153}{2}\) + \(\frac{\frac{1}{2}\left(\frac{1}{2}-1\right)}{2 !}(0.0153)^2\) + ……………..]
= 14 [1 + 0.00765]
= 14 (1.00765) = 14.1071.

v) \(\sqrt[3]{1002}-\sqrt[3]{998}\)

vi) \((1.02)^{3 / 2}-(0.98)^{3 / 2}\)
= (1 + 0.02)^3/2 – (1 – 0.02)^3/2

Question 2.
If |x| is so small that x² and higher powers of x may be neglected, then find approximate values of the following.
i) \(\frac{(4+3 x)^{\frac{1}{2}}}{(3-2 x)^2}\)
ii) \(\frac{\left(1-\frac{2 x}{3}\right)^{\frac{3}{2}}(32+5 x)^{\frac{1}{5}}}{(3-x)^3}\)
iii) \(\sqrt{4-x}\left(3-\frac{x}{2}\right)^{-1}\)
iv) \(\frac{\sqrt{4+x}+\sqrt[3]{8+x}}{(1+2 x)+(1-2 x)^{\frac{-1}{3}}}\)
v) \(\frac{(8+3 x)^{\frac{2}{3}}}{(2+3 x) \sqrt{4-5 x}}\)
Solution:
i) \(\frac{(4+3 x)^{\frac{1}{2}}}{(3-2 x)^2}\)

ii) \(\frac{\left(1-\frac{2 x}{3}\right)^{\frac{3}{2}}(32+5 x)^{\frac{1}{5}}}{(3-x)^3}\)

iii) \(\sqrt{4-x}\left(3-\frac{x}{2}\right)^{-1}\)

iv) \(\frac{\sqrt{4+x}+\sqrt[3]{8+x}}{(1+2 x)+(1-2 x)^{\frac{-1}{3}}}\)

v) \(\frac{(8+3 x)^{\frac{2}{3}}}{(2+3 x) \sqrt{4-5 x}}\)

Question 3.
Suppose s and t are positive and t is very small when compared to s. Then find an approximate value of \(\left(\frac{s}{s+t}\right)^{\frac{1}{3}}-\left(\frac{s}{s-t}\right)^{\frac{1}{3}}\).
Solution:
\(\left(\frac{s}{s+t}\right)^{\frac{1}{3}}-\left(\frac{s}{s-t}\right)^{\frac{1}{3}}\)

Question 4.
Suppose p, q are positive and p is very small when compared to q. Then find an approximate value of \(\left(\frac{q}{q+p}\right)^{\frac{1}{2}}+\left(\frac{q}{q-p}\right)^{\frac{1}{2}}\).
Solution:
\(\left(\frac{q}{q+p}\right)^{\frac{1}{2}}+\left(\frac{q}{q-p}\right)^{\frac{1}{2}}\)

Question 5.
By neglecting x⁴ and higher powers of x, find an approximate value of \(\sqrt[3]{x^2+64}-\sqrt[3]{x^2+27}\).
Solution:
\(\sqrt[3]{x^2+64}-\sqrt[3]{x^2+27}\)

Question 6.
Expand 3√3 in increasing powers of \(\frac{2}{3}\).
Solution:
3√3 = 3^{\(\frac{2}{3}\)}
= \(\left(\frac{1}{3}\right)^{\frac{-3}{2}}\)

Students must practice these TS Inter 2nd Year Maths 2A Important Questions Chapter 1 Complex Numbers to help strengthen their preparations for exams.

TS Inter 2nd Year Maths 2A Complex Numbers Important Questions

Question 1.
Express \(\frac{4+2 i}{1-2 i}+\frac{3 r 4 i}{2+3 i}\) in the form a + bi, a ∈ R, b ∈ R.
Solution:

Question 2.
Find the real and Imaginary parts of the complex number \(\frac{a+i b}{a-i b}\)
Solution:

Question 3.
Express (1 – i)³(1+i) in the of on a+ib.
Solution:
(1 – i)³ (1 + i) = (1 -i)² (1 – 1) (1 + 1)
– (1 +i² – 2i)(1²– i²)
(1 – 1 – 2i) (1 +1) 2(0 – 2i)
= 0  – 4i = 0 + (i – 4)

Question 4.
Find the multiplicative Inverse of 7 + 24i.
Solution:
Since \((x+i y)\left(\frac{x-i y}{x^2+y^2}\right)=1\) it follows that the multiplicative inverse of
(x+iy) is \(\frac{x-i y}{x^2+y^2}\)
Hence the multiplicative inverse of 7 + 24i is
\(\frac{7-24 i}{(7)^2+(24)^2}=\frac{7-24 i}{49+576}=\frac{7-241}{625}\)

Question 5.
Determine the locus of z, z ≠ 2i, such that Re \(\left(\frac{z-4}{z-2 i}\right)=0\)
Solution:
Let z = x + iy, then


The ratio on the R.H.S is zero
i.e., x² – 4x + y² – = 0 if and only if (x – 2)² (y – 1)² =5.
⇔ x,y≠(0, 2) and (x – 2)²+(y – 1)²=5
Hence the locus of the given point representing the complex number is the circle with (2, 1) as centre and \(\sqrt{5}\) units as radius except for the point (0, 2).

Question 6.
If 4x+i(3x – y) = 3 – 6i where x and y are real numbers, then find the values of x and y.
Solution:
We have 4x+i(3x-y)=3+i(-6).
Equating the real and imaginary parts in the above equation, we get
4x = 3, 3x  – y = – 6. Upon solving the simultaneous equations, we get
x = 3/4 and y = 33/4.

Question 7.
If z=2 – 3i, then show that z² – 4z+ 13=0.
Solution:
z = 2 – 3i ⇒ z – 2= – 3i = (z -2)²=(-3i)²
⇒ z² + 4 – 4z = – 9
⇒ z²– 4z+ 13=0

Question 8.
Find the complex conjugate of (3+4i) (2-3i).
Solution:
The given complex number
(3+4i) (2-3i) = 6 – 9i + 8i + 12 = 18 – i
Its complex conjugate = 18 + i.

Question 9.
Show that \(z_1=\frac{2+11 i}{25}, \quad z_2=\frac{-2+i}{(1-2 i)^2}\)
Solution:

Since this complex number is the conjugate of \(\frac{2+11 i}{25}\) the given complex numbers z₁, z₂ are conjugate to each other.

Question 10.
Find the square roots of (-5+ 12f).
Solution:
From 1.2.8, we have

Question 11.
Write \(z=-\sqrt{7}+i \sqrt{21}\) in the polar form.
Solution:

Question 12.
Express – 1 – i in polar form with principal value of the amplitude.
Solution:
Let  – 1  – 1 = r (cos θ + i sin θ).
Then – i = rcosθ,- 1 = r sinθ and tanθ = 1 …………….. (1)
∴ r² = 2, i.e., r = ± \(\sqrt{2}\)
Since r is positive, r = \(\sqrt{2}\)
Since ‘θ’ satisfies – π ≤ 0 < π, the value of θ satisfying the equation (1) is θ \(=\frac{-3 \pi}{4}\)
∴ \(-1-i=\sqrt{2}\left[\cos \left(-\frac{3 \pi}{4}\right)+i \sin \left(\frac{-3 \pi}{4}\right)\right]\)

Question 13.
If the amplitude of \(\left(\frac{z-2}{z-6 i}\right)=\frac{\pi}{2}\),find its locus.
Solution:

The points satisfying (1) and (2) constitute the arc of the circle x² + y² – 2x – Gy = 0 intercepted by the diameter
3x + y – 6 = 0 not containing the origin and excluding the points (0, 6) and (2, 0). Hence this arc is the required locus.

Question 14.
Show that the equation of any circle in the complex plane is of the form
\(\mathbf{z} \overline{\mathbf{z}}+\mathbf{b} \overline{\mathbf{z}}+\overline{\mathbf{b}} \mathbf{z}+\mathrm{c}=\mathbf{0},(\mathbf{b} \in \mathrm{C} ; c \in R)\)
Solution:
Assume the general form of the equation of a circle in Cartesian coordinates as
x²+y²+2gx+2fy+c=0, (g,f ∈ R) …………………. (1)
To write this equation in the complex variable form.
Let (x, y) = z. Then

Question 15.
Show that the complex numbers z satisfying \(z^2+\bar{z}^2=2\) constitute a hyperbola.
Solution:
Substituting z = x + ¡y in the given equation \(z^2+\bar{z}^2=2\) we obtain the Cartesian form of the given equation.
∴ (x+iy)²+(x-iy)²=2
i.e., x² – y² + 2 ixy + x² – y² – 2ixy = 2
or 2x² + 2(iy)² = 2
i.e., x² – y² = 1
Since this equation denotes a hyperbola, all the complex numbers satisfying \(z^2+\bar{z}^2=2\) constitute the hyperbola x² – y² = 1.

Question 16.
Show that the points In the Argand diagram represented by the complex numbers 1 + 3i, 4 – 3i, 5 – 5i are collinear.
Solution:
Let the three complex numbers be represented in the Argand plane by the points
P, Q, R respectively. Then P = (1, 3),Q = (4, – 3) and R = (5, – 5).
The slope of the line segment joining P, Q is \(\frac{3+3}{1-4}=\frac{6}{-3}=-2\)
Similarly, the slope of the line segment joining Q, R is \(\frac{-3+5}{4-5}=\frac{2}{-1}=-2\). Since the slope of PQ is the slope of QR, the points P, Q, R are collinear.

Question 17.
Find the equation of the straight line joining the points represented by (-4 + 3i), (2-3i) in the Argand plane.
Solution:
Take the given points as A= – 4 + 3i = (-4,3)  B=2-3i = (2,-3).
Then the equation of the straight line \(\overline{\mathrm{AB}}\) is
y – 3 = \(\frac{3+3}{-4-2}\) (x +4)
i.e, x + y +1 = 0

Question 18.
z=x+iy represents a point in the Argand plane. Find the locus of z such that lzl = 2.
Solution:
Let z = x + ¡y, Then |z|=2 if and only if
|x + iy| = 2 if and only if 4x² + y² = 2 if and only if x² + y² = 4.
x² + y² = 4 represents a circle with centre at (0,0) and radius 2.
∴ The locus of |z|=2 is the circle x²+ y² = 4.

Question 19.
The point P represents a complex number z in the Argand plane. If the amplitude of \(\mathrm{z} is \frac{\pi}{4}\), determine the locus of P.
Solution:
Let z=x+i y

Question 20.
If the point P denotes the complex number z=x+iy in the Argand plane and if \(\frac{z-i}{z-1}\) is a purely imaginary number, find the locus of P.
Solution:
We note that \(\frac{z-1}{z-1}\) is not defined If z = 1.

i.e., x² + y²– x- y = 0 and (x, y) ≠ (1, 0).
∴ The locus of P is the circle
x² + y²– x – y = 0 excluding the point (1, 0).

Question 21.
Describe geometrically the following subsets of C:
(i) { z ∈ C| | z – 1+i | = 1
(ii) { z ∈ C| | z + 1+i| ≤ 3
Solution:
(i) Let S = {z ∈ C| | z – 1+i | = 1)
If we write z (x, y), then

Hence S is a circle with centre (1, – 1) and radius 1 unit.

Hence s’ is the closed circular disc with centre at (0, – 1) and radius 3 units.