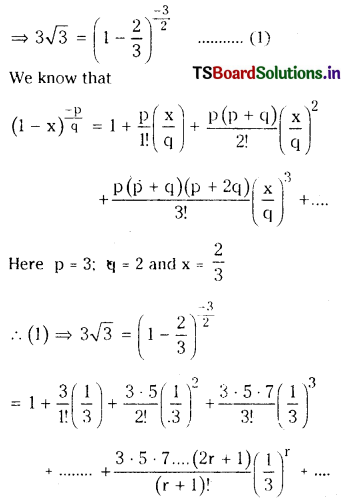TS Inter 2nd Year Maths 2A Solutions Chapter 6 Binomial Theorem Ex 6(c)

Students must practice this TS Intermediate Maths 2A Solutions Chapter 6 Binomial Theorem Ex 6(c) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2A Solutions Chapter 6 Binomial Theorem Ex 6(c)

I.
Question 1.
Find an approximate value of the following corrected to 4 decimal places.
i) \(\sqrt[5]{242}\)
ii) \(\sqrt[7]{127}\)
iii) \(\sqrt[5]{32.16}\)
iv) \(\sqrt{199}\)
v) \(\sqrt[3]{1002}-\sqrt[3]{998}\)
vi) \((1.02)^{3 / 2}-(0.98)^{3 / 2}\)
Solution:
i) \(\sqrt[5]{242}\) = (243 – 1)^{\(\frac{1}{5}\)}
= (243)^{\(\frac{1}{5}\)} (1 – \(\frac{1}{243}\))^{\(\frac{1}{5}\)}
= 3 \(\left[1-\frac{1}{5} \cdot \frac{1}{24.3}+\frac{\frac{1}{5}\left(\frac{1}{5}-1\right)}{2 !}\left(\frac{1}{243}\right)^2-\ldots .\right]\)
= 3 [1 – 0.000823 + ……………]
= 3 (0.999177)
⇒ \(\sqrt[5]{242}\) = 2.997531.

ii) \(\sqrt[7]{127}\)

= 2 (1 – 0.0011161 + ……………)
= 2 (0.99888) = 1.9977.

iii) \(\sqrt[5]{32.16}\)

iv) \(\sqrt{199}\)
= (196 + 3)^1/2
= (196)^1/2 (1 + \(\frac{3}{196}\))^1/2
= 14 (1 + 0.0153)^1/2
= 14 [1 + \(\frac{0.0153}{2}\) + \(\frac{\frac{1}{2}\left(\frac{1}{2}-1\right)}{2 !}(0.0153)^2\) + ……………..]
= 14 [1 + 0.00765]
= 14 (1.00765) = 14.1071.

v) \(\sqrt[3]{1002}-\sqrt[3]{998}\)

vi) \((1.02)^{3 / 2}-(0.98)^{3 / 2}\)
= (1 + 0.02)^3/2 – (1 – 0.02)^3/2

Question 2.
If |x| is so small that x² and higher powers of x may be neglected, then find approximate values of the following.
i) \(\frac{(4+3 x)^{\frac{1}{2}}}{(3-2 x)^2}\)
ii) \(\frac{\left(1-\frac{2 x}{3}\right)^{\frac{3}{2}}(32+5 x)^{\frac{1}{5}}}{(3-x)^3}\)
iii) \(\sqrt{4-x}\left(3-\frac{x}{2}\right)^{-1}\)
iv) \(\frac{\sqrt{4+x}+\sqrt[3]{8+x}}{(1+2 x)+(1-2 x)^{\frac{-1}{3}}}\)
v) \(\frac{(8+3 x)^{\frac{2}{3}}}{(2+3 x) \sqrt{4-5 x}}\)
Solution:
i) \(\frac{(4+3 x)^{\frac{1}{2}}}{(3-2 x)^2}\)

ii) \(\frac{\left(1-\frac{2 x}{3}\right)^{\frac{3}{2}}(32+5 x)^{\frac{1}{5}}}{(3-x)^3}\)

iii) \(\sqrt{4-x}\left(3-\frac{x}{2}\right)^{-1}\)

iv) \(\frac{\sqrt{4+x}+\sqrt[3]{8+x}}{(1+2 x)+(1-2 x)^{\frac{-1}{3}}}\)

v) \(\frac{(8+3 x)^{\frac{2}{3}}}{(2+3 x) \sqrt{4-5 x}}\)

Question 3.
Suppose s and t are positive and t is very small when compared to s. Then find an approximate value of \(\left(\frac{s}{s+t}\right)^{\frac{1}{3}}-\left(\frac{s}{s-t}\right)^{\frac{1}{3}}\).
Solution:
\(\left(\frac{s}{s+t}\right)^{\frac{1}{3}}-\left(\frac{s}{s-t}\right)^{\frac{1}{3}}\)

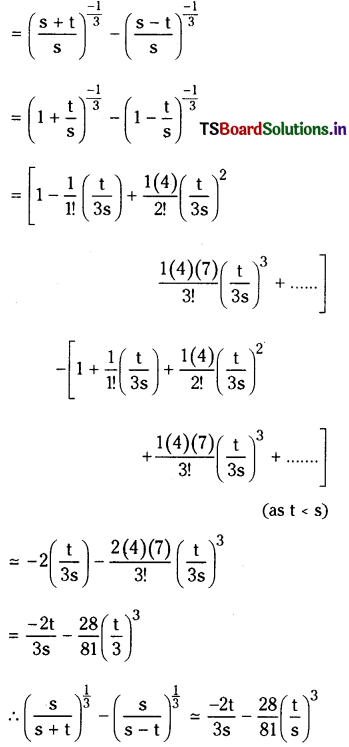
Question 4.
Suppose p, q are positive and p is very small when compared to q. Then find an approximate value of \(\left(\frac{q}{q+p}\right)^{\frac{1}{2}}+\left(\frac{q}{q-p}\right)^{\frac{1}{2}}\).
Solution:
\(\left(\frac{q}{q+p}\right)^{\frac{1}{2}}+\left(\frac{q}{q-p}\right)^{\frac{1}{2}}\)

Question 5.
By neglecting x⁴ and higher powers of x, find an approximate value of \(\sqrt[3]{x^2+64}-\sqrt[3]{x^2+27}\).
Solution:
\(\sqrt[3]{x^2+64}-\sqrt[3]{x^2+27}\)

Question 6.
Expand 3√3 in increasing powers of \(\frac{2}{3}\).
Solution:
3√3 = 3^{\(\frac{2}{3}\)}
= \(\left(\frac{1}{3}\right)^{\frac{-3}{2}}\)