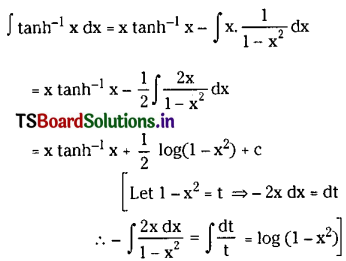TS Inter 2nd Year Maths 2B Solutions Chapter 6 Integration Ex 6(c)

Students must practice this TS Intermediate Maths 2B Solutions Chapter 6 Integration Ex 6(c) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 6 Integration Exercise 6(c)

I. Evaluate the following integrals.

Question 1.
∫x sec²x dx on I ⊂ R – {\(\frac{(2 n+1) \pi}{2}\) : n is an integer}.
Solution:
We use the formula for integration by parts which state that

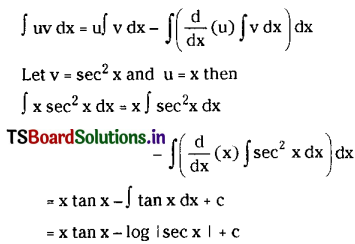
Question 2.
\(\int e^x\left(\tan ^{-1} x+\frac{1}{1+x^2}\right) d x\), x ∈ R.
Solution:

Question 3.
\(\int \frac{\log x}{x^2} d x\) on(0, ∞).
Solution:

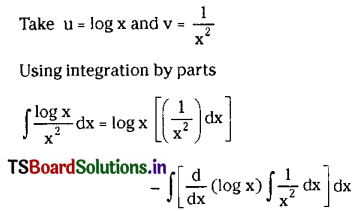
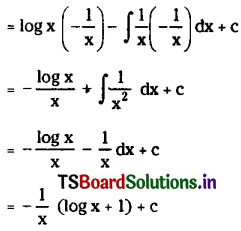
Question 4.
∫(log x)² dx on (0, ∞).
Solution:
Take (log x)² = u and 1 = v.
Then by integration by parts,
∫(log x)² . 1 . dx = (log x)² . x – ∫2 (log x) \(\frac{1}{x}\) . x dx
= x(log x)² – 2 ∫log x . 1 . dx
= x(log x)² – 2[logx . x – ∫\(\frac{1}{x}\) . x dx]
= x(log x)² – 2x[log x] + 2x + c

Question 5.
∫e^x (sec x + sec x tan x) dx on I ⊂ R – {(2n + 1)\(\frac{\pi}{2}\) : n ∈ Z}.
Solution:
Let f(x) = sec x then f'(x) = sec x tan x
∴ Using ∫e^x [f(x) + f'(x)] dx = e^x f(x) + c
we have ∫e^x (sec x + sec x tan x) dx = e^x sec x + c

Question 6.
∫e^x cos x dx on R.
Solution:
Let I = ∫e^x cos x dx
and take u = e^x and v = cos x.
Then using integration by parts,
I = e^x (sin x) – ∫e^x sin x dx
= e^x (sin x) – [e^x(-cos x) – ∫e^x (-cos x) dx]
= e^x sin x + e^x cos x – ∫e^x cos x dx
= e^x (sin x + cos x) – 1
2I = e^x (sin x + cos x)
I = \(\frac{1}{2}\) e^x (sin x + cos x) + c
∴ ∫e^x cos x dx = \(\frac{1}{2}\) e^x (sin x + cos x)

Question 7.
∫e^x (sin x + cos x) dx on R.
Solution:
Take f(x) = sin x then f'(x) = cos x
So by using formula ∫e^x [f(x) + f'(x)] dx = e^x f(x) + c
we have ∫e^x (sin x + cos x) dx = e^x sin x + c.

Question 8.
∫(tan x + log sec x) e^x dx on ((2n – \(\frac{1}{2}\))π, (2n + \(\frac{1}{2}\))π), n ∈ Z.
Solution:
Take f(x) = log|sec x| then f'(x) = \(\frac{1}{\sec x}\) (sec x tan x) = tan x
So by the formula ∫e^x [f(x) + f'(x)] dx = e^x f(x) + c
we have ∫(tan x + log sec x) e^x dx = e^x log|sec x| + c

II. Evaluate the following integrals.

Question 1.
∫xⁿ log x dx on (0, ∞), n is a real number and n ≠ -1.
Solution:
Take u = log x and v = xⁿ
applying integration by parts,

Question 2.
∫log(1 + x²) dx on R.
Solution:
Take log(1 + x²) = u and 1 = v then
using integration by parts, we get

Question 3.
∫√x log x dx on (0, ∞).
Solution:
Take u = log x and v = x^1/2 and
using integration by parts, we get

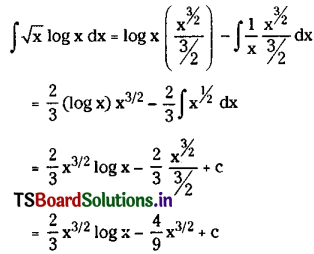
Question 4.
\(\int e^{\sqrt{x}} d x\) on (0, ∞).
Solution:

Question 5.
∫x² cos x dx on R.
Solution:
Take x² = u and cos x = v,
and using integration by parts, we get
∫x² cos x dx = x² (sin x) – ∫2x sin x dx
= x² sin x – [2x(-cos x) – ∫2 . (-cos x) dx]
= x² sin x + 2x cos x – 2∫cos x dx
= x² sin x + 2x cos x – 2 sin x + c

Question 6.
∫x sin²x dx on R.
Solution:

Question 7.
∫x cos²x dx on R.
Solution:

Question 8.
∫cos√x dx on R.
Solution:
∫cos√x dx = ∫\(\frac{1}{\sqrt{x}}\) √x cos√x dx
Taking √x = t, we get \(\frac{1}{2 \sqrt{x}}\) dx = dt
⇒ \(\frac{\mathrm{dx}}{\sqrt{\mathrm{x}}}\) = 2 dt
∴ ∫cos √x dx = 2∫t cos t dt
using Integration by parts,
= 2[t(sin t) – ∫1 . sin t dt]
= 2[t sin t + cos t + c]
= 2[√x sin √x + cos √x ] + c

Question 9.
∫x sec²2x dx on I ⊂ R \ {(2nπ + 1) \(\frac{\pi}{4}\) : n ∈ Z}
Solution:
Taking x = u and sec²2x = v,
and applying integration by parts we get
∫x sec²2x dx = x(\(\frac{1}{2}\) tan 2x – ∫1 . \(\frac{1}{2}\) tan 2x dx
= \(\frac{x}{2}\) tan 2x – \(\frac{1}{2}\) ∫tan 2x dx
= \(\frac{x}{2}\) tan 2x – \(\frac{1}{4}\) log|sec 2x| + c

Question 10.
∫x cot²x dx on I ⊂ R \ {nπ : n ∈ Z).
Solution:
∫x cot²x dx = ∫x(cosec²x – 1) dx = ∫x cosec²x dx – ∫x dx
Taking u = x and v = cosec²x on the first integral
and using integration by parts we get
∫x cot²x dx = x(-cot x) – ∫1 . (-cot x) dx – \(\frac{x^2}{2}\)
= -x cot x + ∫cot x dx – \(\frac{x^2}{2}\)
= -x cot x + log|sin x| – \(\frac{x^2}{2}\) + c

Question 11.
∫e^x (tan x + sec²x) dx on I ⊂ R \ {(2n + 1)\(\frac{\pi}{2}\) : n ∈ Z}.
Solution:
Let f(x) = tan x, then f'(x) = sec²x
So by the formula ∫e^x [f(x) + f'(x)] dx = e^x f(x) + c
we have ∫e^x (tan x + sec²x) dx = e^x tan x + c

Question 12.
∫\(e^x\left(\frac{1+x \log x}{x}\right) d x\) on (0, ∞). (Mar. ’13)
Solution:

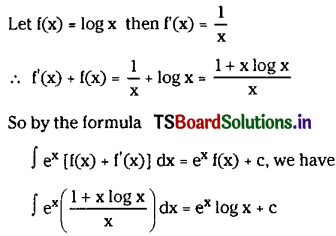
Question 13.
∫e^ax sin bx dx on R, a, b ∈ R.
Solution:
Let I = ∫e^ax sin bx dx
Taking u = e^ax and v = sin bx
and applying integration by parts

Question 14.
\(\int \frac{x e^x}{(x+1)^2} d x\) on I ⊂ R \ {-1}.
Solution:

Question 15.
\(\int \frac{d x}{\left(x^2+a^2\right)^2}\), (a > 0) on R.
Solution:
Take substitution x = a tan θ
so that dx = a sec²θ dθ

Question 16.
∫e^x log(e^2x + 5e^x + 6) dx on R.
Solution:

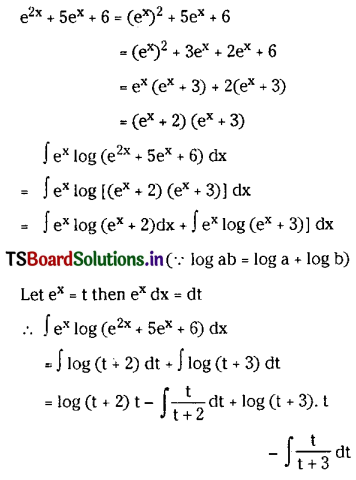
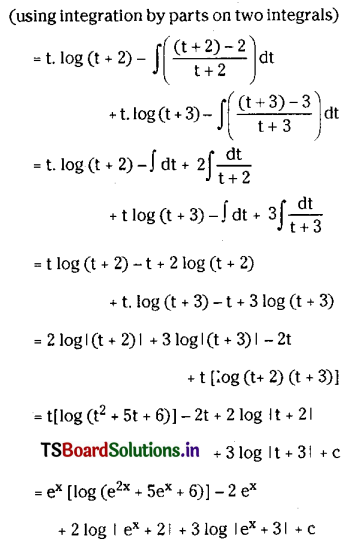
Question 17.
\(\int e^x \frac{(x+2)}{(x+3)^2} d x\) on I ⊂ R \ {-3}.
Solution:

Question 18.
∫cos(log x) dx on (0, ∞).
Solution:
Let I = ∫cos (log x) dx = ∫cos (log x) . 1 dx
Take u = cos (log x) and v = 1
and using integration by parts successively.
I = cos (log x) . x – ∫-sin (log x) \(\frac{1}{x}\) . x . dx
= x cos (log x) + ∫sin(log x) dx
= x cos (log x) + sin (log x) . x – ∫cos (log x) \(\frac{1}{x}\) . x . dx
= x cos (log x) + x . sin(log x) – ∫cos (log x) dx
= x [cos (log x) + sin (log x)] – ∫cos (log x) dx
= x [cos (log x) + sin (log x)] – I
∴ 2I = x [cos (log x) + sin (log x)]
⇒ I = \(\frac{x}{2}\) [cos (log x) + sin (log x)] + c
∴ ∫cos (log x) dx = \(\frac{x}{2}\) [cos (log x) + sin (log x)] + c

III. Evaluate the following integrals.

Question 1.
∫x tan^-1x dx, x ∈ R.
Solution:
Let u = tan^-1x and v = x then using integration by parts

Question 2.
∫x² tan^-1x dx, x ∈ R.
Solution:
Take u = tan^-1x and v = x²
and apply integration by parts we get

Question 3.
\(\int \frac{\tan ^{-1} x}{x^2} d x\), x ∈ I ⊂ R \ {0}.
Solution:

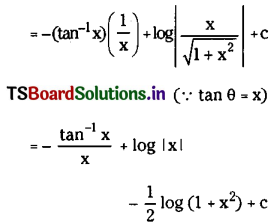
Question 4.
∫x cos^-1x dx, x ∈ (-1, 1).
Solution:
Let cos^-1x = θ then cos θ = x
⇒ dx = -sin θ dθ
∴ ∫x cos^-1x dx = ∫θ cos θ (-sin θ dθ) – \(\frac{1}{2}\) ∫θ sin 2θ dθ
Using integration by parts by taking u = θ, v = sin 2θ we get

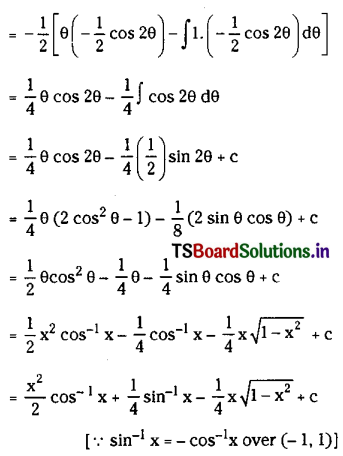
Question 5.
∫x² sin^-1x dx, x ∈ (-1, 1).
Solution:
Let sin^-1x = θ then sin θ = x
⇒ dx = cos θ dθ
∴ ∫x² sin^-1x dx = ∫θ sin²θ cos θ dθ
Using integration by parts
by choosing functions u = θ and v = sin²θ cos θ, we get

Question 6.
∫x log(1 + x) dx, x ∈ (-1, ∞).
Solution:
Take u = log(1 + x) and v = x
and apply integration by parts

Question 7.
∫sin√x dx on (0, ∞).
Solution:
\(\int \frac{\sqrt{x}}{\sqrt{x}} \sin \sqrt{x} d x\)
Let √x = t then \(\frac{1}{2 \sqrt{x}}\) dx = dt
⇒ \(\frac{d x}{\sqrt{x}}\) = 2 dt
∴ ∫sin √x dx = 2∫t sin t dt,
using Integration by parts by taking u = t and v = sin t, we get
= 2[t(-cos t) – ∫1 . (-cos t) dt]
= 2[-t cos t + ∫cos t dt]
= 2[-t cos t + sin t] + c
= 2[sin √x – √x cos √x ] + c

Question 8.
∫e^ax sin(bx + c) dx, (a, b, c ∈ R, b ≠ 0) on R.
Solution:
Let I = ∫e^ax sin (bx + c) dx, taking u = e^ax and v = sin (bx + c)
and applying integration by parts,

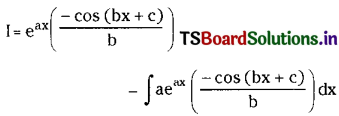
Question 9.
∫a^x cos 2x dx on R (a > 0 and a ≠ 1).
Solution:
Let I = ∫a^x cos 2x dx
using integration by parts by taking cos 2x = u and a^x = v, we have

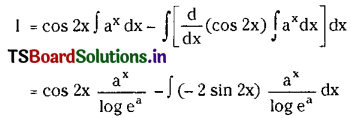
Question 10.
\(\int \tan ^{-1}\left(\frac{3 x-x^3}{1-3 x^2}\right) d x\) on I ⊂ R – \(\left\{-\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}\right\}\).
Solution:

Question 11.
∫sinh^-1x dx on R.
Solution:
Take sinh^-1x = u and v = 1,
Applying integration by parts we get

Question 12.
∫cosh^-1x dx on [1, ∞).
Solution:
∫cosh^-1x dx = ∫cosh^-1x . 1 . dx
Take u = cosh^-1x and v = 1 then

Question 13.
∫tanh^-1x dx on (-1, 1).
Solution:
∫tanh^-1x dx = ∫tanh^-1x . 1 . dx
Take u = tanh^-1x and v = 1
and apply integration by parts we get