Students can practice 10th Class Maths Solutions Telangana Chapter 4 Pair of Linear Equations in Two Variables Ex 4.2 to get the best methods of solving problems.
TS 10th Class Maths Solutions Chapter 4 Pair of Linear Equations in Two Variables Exercise 4.2
Question 1.
The ratio of incomes of two persons is 9: 7 and the ratio of their expenditures is 4 : 3. If each of them manages to save
₹ 2,000 per month, find their monthly income.
Solution:
Let the income of the first person be ₹ 9x and that of the second person be ₹ 7x.
Further, let the expenditure of the first person and the second person be ₹ 4y and 3y respectively.
Then, the saving of first person = 9x – 4y
By problem, 9x – 4y = 2,000 —— (1)
The saving of second person = 7x – 3y
Solving (1) and (2), we get
We equate the coefficients of ‘y’ in the equations.
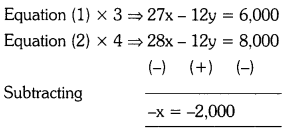
∴ x = 2,000
Substitute x = 2,000 in equation (1), we get
9 × 2,000 – 4y = 2,000
18,000 – 4y = 2,000
-4y = 2,000 – 18,000 = -16,000
∴ y = \(\frac{-16000}{-4}\) = 4,000
Therefore, monthly income of the first person = ?9x
= ₹ 9 × 2,000
= ₹ 18,000
Monthly income of the second person = ₹ 7x
= ₹ 7 × 2,000
= ₹ 14,000
Question 2.
The sum of a two digit number and the number obtained by reversing the digits is 66. If the digits of the number differ by 2, find the number. How many such numbers are there ?
Solution:
Let the digit at units place be x.
And the digit at tens place be y.
The number will be yx.
The value of the number = y × 10 + x × 1
= 10y + x
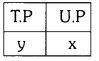
Number obtained by reversing the digits = xy
Then the value of the reversed number = 10 × x + y × 1
= 10x + y
By problem, we have
(10y + x) + (10x + y) = 66
⇒ 11x + 11y = 66
⇒ x + y = 6 —– (1)
It is given that the digits differ by 2.
So, x – y = 2 (or) y – x = 2 —- (2)
Solving (1) and (2), we get
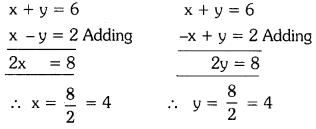
Substitute x = 4 in (1), we get
x + y = 6 ⇒ y = 6 – 4 = 2
Substitute y = 4 in (1),
x + y = 6 ⇒ x = 6 – 4 = 2
∴ The required number is 24.
∴ The required number is 42.
There are two numbers (i.e.,) 24 and 42.
![]()
Question 3.
The larger of two supplementary angles exceeds the smaller by 18°. Find the angles.
Solution:
Two angles are said to be supplementary if their sum is 180°.
Let the smaller supplementary angle be x°. and the larger supplementary angle be y°.
We know that sum of these two angles is 180°.
∴ x + y = 180° —- (1)
The larger angle exceeds the smaller by 18°. Then, y = x + 18
⇒ -x + y = 18 —- (2)
Solving (1) & (2), we get
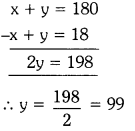
Substitute y = 99 in (1), we get
x + 99 = 180
⇒ x = 180 – 99 = 81
Therefore, the required angles are 81°, 99°.
Question 4.
The taxi charges in Hyderabad are fixed along with the charge for the distance covered. For a distance of 10 km., the charge paid is ₹ 220. For a journey of 15 km, the charge paid is ₹ 310.
i) What are the fixed charges and charge per km ?
ii) How much does a penon have to pay for travelling a distance of 25 km?
Solution:
Let the fixed charge be ₹ x.
And charge per km be ₹y.
For a distance of 10km, the charge paid is ₹ 220.
Then x + 10y = 220 —– (1)
For a distance of 15 km, the charge paid is ₹ 310.
Then, x + 15y = 310 —- (2) ;
Solving (1) & (2), we get
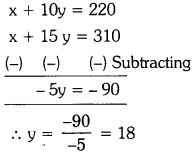
Substitute y = 18 in equation (1), we get
x + (10 × 18) = 220
x + 180 = 220
∴ x = 220 – 180 = 40
Fixed charge = ₹ 40
Charge per km = ₹ 18
∴ Charge for 25 km = ₹ 450
Question 5.
A fraction becomes if \(\frac{4}{5}\) is added to both numerator and denominator. If, however, 5 is subtracted from both numerator and denominator, the fraction becomes \(\frac{1}{2}\). What is the fraction ? (AP Mar. 15)
Solution:
Let the fraction be; \(\frac{x}{y}\)
If 1 is added to both numerator and denominator then the fraction = \(\frac{x+1}{y+1}\)
By problem, \(\frac{x+1}{y+1}\) = \(\frac{4}{5}\)
⇒ 5(x + 1)= 4(y + 1)
⇒ 5x + 5 = 4y +4
⇒ 5x – 4y = 4 – 5 = -1
⇒ 5x – 4y = -1 —- (1)
If 5 is subtracted from both numerator and denominator, then
the fraction = \(\frac{x-5}{y-5}\)
By problem, \(\frac{x-5}{y-5}\) = \(\frac{1}{2}\)
⇒ 2(x – 5) = 1(y – 5)
⇒ 2x – 10 = y – 5
⇒ 2x – y = -5 + 10 = 5
⇒ 2x – y = 5 —- (2)
Solving (1) & (2), we get
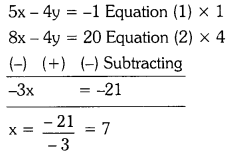
Substitute x = 7 in (2),
⇒ 2 × 7 – y = 5
⇒ 14 – y = 5
⇒ -y = 5 – 14 = -9
∴ y = 9
∴ The required fraction is \(\frac{7}{9}\).
![]()
Question 6.
Places A and B are 1oo km apart on a highway. One car starts from A and another from B at the same time at different speeds. if the cars travel in the same direction, they meet in 5 hours. If they travel towards each other, they meet in 1 hour. What are the speeds of the two cars?
Solution:
Let the speed of the car that starts from A be x kmph.
Let the speed of the car that starts from B be y kmph.
Distance between A and B is 1oo km.
![]()
∴ Speed × Time = Distance travelled
(x – y) × 5 = 100
5x – 5y = 100
⇒ x – y = 20 —- (1)
If the two cars travel in the opposite direction, their relative speed will be (x + y) kmph. It is also given that the cars will meet in 1 hour.
∴ Speed × Time = Distance travelled
(x + y) × 1 = 100
⇒ x + y = 100 —- (2)
Solving (1) & (2), we get

Substitute x = 60 in equation (2),
60 + y = 100
∴ y = 100 – 60 = 40
∴ The speeds of the cars are 60 kmph and 40 kmph.
Question 7.
Two angles are complementary. The larger angle is 3° less than twice the measure of the smaller angle. Find the
measure of each angle.
Solution:
Two angles are said to be complementary if their sum is 90°.
Let the smaller angle be x° and the larger angle y°.
∴ x + y = 90° —- (1)
Given that the larger angle is 30 less than twice the measure of the smaller angle.
∴ y = 2x – 3
⇒ 2x – y = 3 — (2)
Solving (1) & (2), we get
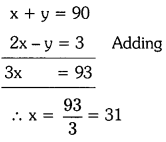
Substitute x = 31 in (1),
Then, 31 + y = 90
∴ y = 90 – 31 = 59
The two angles are 31° and 59°
Question 8.
An algebra textbook has a total of 1382 pages. It is broken up into two parts. The second part of the book has 64 pages
more than the first part. How many pages are in each part of the book ?
Solution:
Let the number of pages in the first part of algebra textbook be ‘x’ and that of second part be ‘y’. The textbook contains 1382 pages.
∴ x + y = 1382 —- (1)
It is given that the second part of the book has 64 pages more than the first part.
∴ y = x + 64
⇒ x – y = – 64 —- (2)
Solving (1) & (2), we get
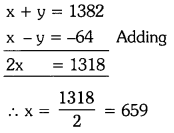
Substitute x = 659 in (1), we get
659 + y = 1382
∴ y = 1382 – 659 = 723
First part of the book has 659 pages whereas the second part has 723 pages.
Question 9.
A chemist has two solutions of hydrochloric acid in stock. One is 50% solution and the other is 80% solution. How much of each should be used to obtain 100 ml of a 68% solution ?
Solution:
Let 50% solution to be used be ‘x’ ml.
And 80% solution to be used be ‘y’ ml.
Quantity of solution to be obtained = 100 ml
∴ x + y = 100 —– (1)
50% of ‘x’ ml = \(\frac{x \times 50}{100}\) = \(\frac{1}{2} \mathrm{x}\)
80% of ‘y’ ml = \(\frac{\mathrm{y} \times 80}{100}\) = \(\frac{4}{5} \mathrm{y}\)
By problem, \(\frac{1}{2}\)x + \(\frac{4}{5}\)y = 68
Multiplying each terms by 10, we get
[\(\frac{1}{2}\)x × 10] + [\(\frac{4}{5}\)y × 10] = 68 × 10
5x + 8y = 680 —– (2)
Solving equation (1) & (2), we have

∴ y = \(\frac{180}{3}\) = 60
Substitute y = 60 in (1), we have
x + y = 100
x + 60 = 100
∴ x = 100 – 60 = 40
Therefore, 50% solution to be used = 40 ml.
80% solution to be used 60 ml
![]()
Question 10.
Suppose you have ₹ 12,000 to invest. You have to invest some amount at 10% and the rest at 15%. How much should be
invested at each rate to yield 12% on the total amount invested?
Solution:
Total amount to be invested = ₹ 12,000/-
Let the amount invested at 10% be ₹ x.
Let the amount invested at 15% be ₹ y.
∴ x + y = ₹ 12,000 —- (1)
Amount yielded at 10% of
x = \(\frac{x \times 10}{100}\) = \(\frac{x}{10}\)
Amount yielded at 15% of
y = \(\frac{y \times 15}{100}\) = \(\frac{3 \mathrm{y}}{20}\)
yielded at 12% of ₹ 12,000
= \(\frac{12000 \times 12}{100}\) = 1440
∴ \(\frac{x}{10}\) + \(\frac{3 y}{20}\) = \(\frac{1440}{1}\)
∴ 2x + 3y = 28800 —- (2)
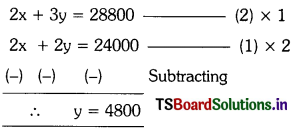
Substitute y = 4800 in (1), we get
x + 4800 = 12000
∴ x = 12000 – 4800 = 7200
The amounts to be invested at 10% and 15% are ₹ 7,200 and ₹ 4,800.