TS Inter 2nd Year Maths 2B Parabola Important Questions

Students must practice these TS Inter 2nd Year Maths 2B Important Questions Chapter 3 Parabola to help strengthen their preparations for exams.

TS Inter 2nd Year Maths 2B Parabola Important Questions

Very Short Answer Type Questions

Question 1.
Find the coordinates of the vertex and focus and the equations of the directrix and axis of the following parabolas.
(i) y² = 16x
Comparing with y² = 4ax, we have 4a = 16
a = 4
Vertex = (0, 0)
Focus = (a, 0) = (4, 0)
Equation of clirectrix is x + a = 0 ⇒ x + 4 = 0
Equation of axis is y = 0.

(ii) x² =-4y
Comparing with x² = – 4ay, we have 4a = 4 ⇒ a = I
∴ Vertex = (0. 0)
Focus =(0,-a)=(0,-1)
Equation of directrix is y-a=0=y-1 =0
Equation of axis is x – 0.

(iii) 3x- 9x + 5y – 2 = 0
Given equation is 3x² – 9x – 5y +2
= 3(x² – 3x) =- \(5\left(\mathrm{y}-\frac{2}{5}\right)\)

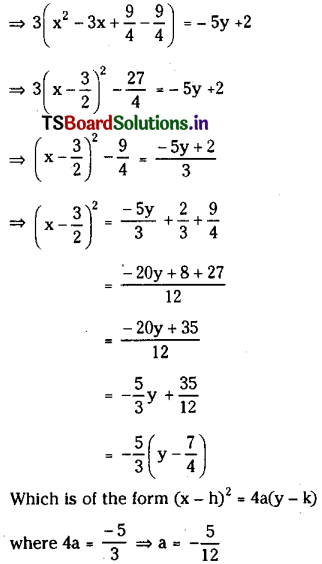
(i) Vertex (h, k) \(\left(\frac{3}{2}, \frac{7}{4}\right)\)
(ii) Focus=(h,k,-a) = \(\left(\frac{3}{2}, \frac{7}{4}-\frac{5}{12}\right)=\left(\frac{3}{2}, \frac{4}{3}\right)\)
(iii) Equation of directrix is y – k = 0
⇒ 6y – 13= 0
(iv) Equation of axis x – h = 0
= x = \(\frac{3}{2}\) – 0 ⇒ 2x – 3 = 0

(iv) y² – x + 4y + 5 = 0
The given equation can be written as
y² + 4y – x – 5
9 + 4y + 4 – x – 1
(y+2)² – (x-1)
Comparing with (y – k)² – 4a (x – h)
we have h=1, k = -2, a= \(\frac{1}{4}\)
(i) Vertex = (h, k) – (1, -2)
(ii) Focus = (h+a,k) = \(\left(\frac{5}{4},-2\right)\)
(iii) Directrix is x – h + a = 0 ⇒ 4x – 3 = 0
(Iv) Equation of axis is y-k=0 ⇒ y+2 = 0

Question 2.
Find the equation of parabola whose vertex is (3-2) and focus is (3,1)
Solution:
The abscissae of vertex and focus is ‘3’.
Hence the axis of the parabola is x -3, a line parallel to y-axis, focus is above the vertex.
a = SA = \(\sqrt{(3-3)^2+(1+2)^2}=3\)
(∵ A=(3,-2) S= (3,3))
∴ Equation of the parabola
(x-h)² =4a (y-k)
(x-3)²– 12(y+2)
(∵ A = (h,k) =3,-2 and S (h, k-a)]

Question 3.
Find the coordinates of the points on the parabola y² = 2x whose focal distance is \(\frac{5}{2}\)
Solution:
Let P(x₁, y₁) be any point on the parabola
y² = 2x whose focal distance is \(\frac{5}{2}\) then
\(y_1^2=2 x_1\) and \( x_1+a=\frac{5}{2} \Rightarrow \frac{5}{2}-\frac{1}{2}\)
Where 4a=2 ⇒ a = \(\frac{1}{2}\)
∴ x₁= 2, and since y_1² = 2x₁ we have
y_1² = 4 = y₁ = ± 2
∴ The required points are (2, 2), (2, -2).

Short Answer Type Questions

Question 1.
Find the equation of the parabola passing through the points (- 1, 2), (1, – 1) and (2, 1) and having its axis parallel to the x-axis.
Solution:
Since the axis is parallel to x – axis the equation of the parabola is in the form of
x – ly²+my+n ……………. (1)
Given that the parabola passes through the points (-1, 2), (1, -1) and (2, 1) we have
– 1 = 14l+2m+n ……………………. (2)
1= l – m+n ……………….. (3)
2=l+m+n …………………….. (4)
From (2) and (3), -2 = 3l + 3m

∴  Equation of required parabola is
\(x=-\frac{7}{6} y^2+\frac{1}{2} y+\frac{8}{3}\)

Question 2.
A double ordinate of the curve y² = 4ax is of length 8a. Prove that the lines from the vertex to its ends are at right angles.
Solution:

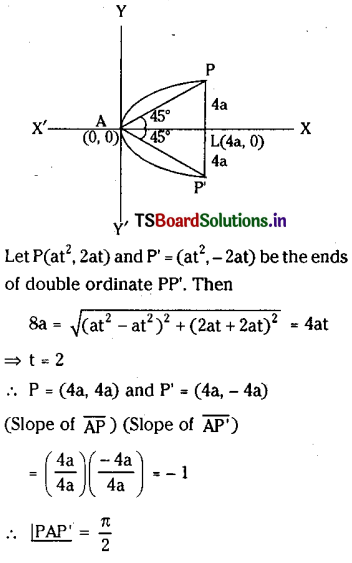
Question 3.
Find the condition for the straight line lx + my + n=0 to be a tangent to the parabola y² = 4ax and find the coordinates
of the point of contact.
Solution:
Let the line ix + my + n = 0 …………….. (1) touches
y² = 4ax …………….. (2) at the point (x₁, y₁).
Then the equation of tangent at (x₁, y₁) to the parabola
y²=4ax is yy₁– 2ax – 2ax₁=0 …………. (2)
Since (1) and (2) represent the same line, coefficients are proportional.

Question 4.
Show that the straight line 7x+6y=13 is a tangent to the parabola y²– 7x – 8y + 14 = 0 and find the point of contact
Solution:
Given line is 7x + 6y – 13 = 0 ……………….. (1)
and parabola is y² – 7x – 8y+ 14 = 0 ………………..(2)
From (1),

Point of contact is (1, 1) and this point satisfies (1) and (2). Hence (1) is tangent to the parabola (2).

Question 5.
From an external point P, tangents are drawn to the parabola y² = 4ax and these tangents make angles θ₁, θ₂ with its axis such that tan θ₁+ tan θ₂ is a constant b. Then show that P lies on the line y = bx.
Solution:
Let P(x₁, y₁) be the external point.
Any tangent to the parabola is of the form
y=mx+ \(\frac{\mathrm{a}}{\mathrm{m}}\) =mx₁– my₁+a = 0
Let the roots of (1) be 4 m₁, m₂ ………………  (1)
Then m₁ + m₂ = \(\frac{y_1}{x_1}\) and m₁ + m₂ = \(\frac{\mathrm{a}}{\mathrm{x}_1}\)
The tangents make angles θ₁ and θ₂ with the axis such that m₁ = tan θ₁ and m₂= tan θ₂
Given tan θ₁ + tan θ₂ = b
⇒ m₁ + m₂ = b
\(\frac{\mathrm{y}_1}{\mathrm{x}_1}\) = b ⇒ y₁ = bx₁
∴ Locus of (x₁, y₂) is y = bx.

Question 6.
Show that the common tangents to the parabola y² = 4ax and x² = 4by is xa^1/3 + yb^1/3 + xa^2/3 yb^2/3
Solution:
The equations of the parabolas are
y² = 4ax ………………….. (1)
and x² = 4by ………………… (2)
Equation of any tangent to (1) is of the form
y=mx+\(\frac{\mathrm{a}}{\mathrm{m}}\) ………….. (3)
lf the line (3) is tangent to (2) also the point of intersection of (2) and (3) coincide.
From (3) and (2)
x² = 4b \(\left(\mathrm{mx}+\frac{\mathrm{a}}{\mathrm{m}}\right)\)
⇒ mx² – 4bm²x – 4ab = 0
which should have equal roots.
∴ Therefore the discriminant is zero.

Long Answer Type Questions

Question 1.
Find the equation of a parabola in his standard form.
Solution:

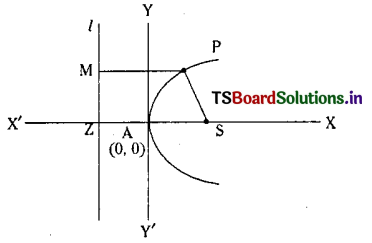
Let S be the focus, l be the directrix as shown in the figure. Let Z be the projection of S on I and A be the mid point of \(\overline{\mathrm{SZ}}\). A lies on the parabola since SA = AZ. A is the vertex of the parabola. YY’ is parallel to the clirectrix ‘l’.
Let S=(a,0), (a>0) then Z =(-a, 0) and the equation of the directrix is x + a = 0.
Let P(x, y) be a point on the parabola and PM is the perpendicular distance from P to x + a = 0.
Then by definition \(\frac{\mathrm{SP}}{\mathrm{PM}}\) = e = 1
= SP² = PM²
= (x- a)² +(y-0)² = (x+a)²
= y² =(x+a)²-(x-a)² = 4ax
Conversely also if P(x, y) is a point such that y² = 4ax then SP = PM.
∴ P(x, y) lies on the locus. Equation of parabola in standard form is y² = 4ax.

Question 2.
(i) If the coordinates of the ends of a focal chord of the parabola y² = 4ax are (x₁, y₁) and (x₂, y₂) then prove that
x₁x₂ = a² and y₁y₂ = – 4a².
(ii) For a focal chord PQ of the parabola y² = 4ax if SP =l and SQ = l’ then prove that \(\frac{1}{l}+\frac{1}{l}=\frac{1}{a}\)
Solution:
(i) Let P(x₁, y₁) = (at₁², 2at₁)
and Q(x₂, y₂) = (at₂², 2at₂)
be two end points of a focal chord and S(a, 0) be the focus of the parabola y² = 4ax. PSQ is a focal chord P, S, Q are collinear.

(ii) Let P(at²₁, 2at₁) and Q (at²₂, 2at₂) be the extremities of a focal chord of parabola such that t₁,t₂ = – 1.

Question 3.
If Q is the foot of the perpendicular from a points P on the parabola y² = 8(x -3) to its directrix. S is the focus of parabola and if SPQ is an equilateral triangle then find the length of side of triangle.
Solution:
Given equation of parabola is
(y – 0)² = 8(x – 3)
which is of the form (y – k)² = 4a (x – h)
where 4a = 8 ⇒ a = 2
∴ Vertex = (h, k) = (3,0)
and focus = (h + a, k) = (3 +2, 0) =  (5, 0)

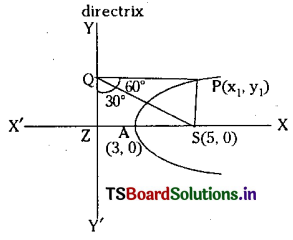
Since PQS is an equilateral triangle.
\(\angle \mathrm{SQP}=60^{\circ} \Rightarrow \angle \mathrm{SQZ}=30^{\circ}\)
Also in ΔSZQ , we have sin 30° = \(\frac{\mathrm{SZ}}{\mathrm{SQ}}\)

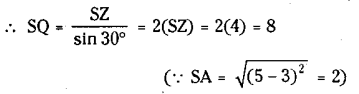
Hence length of each side of the triangle is 8

Question 4.
The cable of a uniformly loaded suspension bridge hangs In the form of a parabola. The roadway which is horizontal and 72mt. long is supported by vertical wires attached to the cable. The longest being 30 mts. and the shortest being 6 mts. Find the length of the supporting wire attached to the roadway 18 mts. from the middle.
Solution:

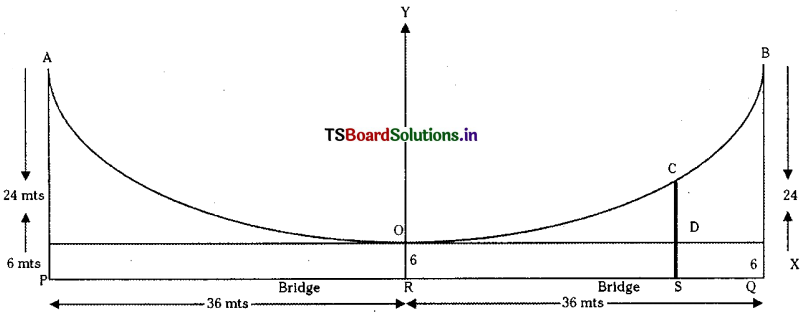
Let AOB be the cable [O is the lowest point and A, B are highest points). Let PRQ be the suspension bridge suspended with PR – RQ = 36 mts.
PA = QB = 30 mts (longest wire)
OR = 6 mts (shortest wire)
∴ PR = RQ = 36 mts. We take O as origin of coordinates at O, X-axis along the tangent \(\overline{\mathrm{RO}}\). So the equation of the cash is x² = 4ay for some a> 0.
∴ B(36,24) and B is a point on x²=4ay
We have (36)² = 4a(24)
⇒ 4a = \(\frac{36 \times 36}{24}\) = 54 mts
If RS = 18 mts and SC is the vertical through S meeting the cable at ‘C’ and the X- axis at D.
Then SC is the length of the required wire.
Let SC = l mts then DC = L – 6 mts.
∴ C = (18, 1 – 6) which lies on x² = 4ay
⇒ (18)² = 4a (l – 6)
⇒ (18)²= 54 (l -6)
⇒ l – 6 = \(\frac{18 \times 18}{54}\) = 6
⇒ l = 12.

Question 5.
Prove that the normal chord at the point other than origin whose ordinate is equal to Its abscissa subtends a right angle at the focus
Solution:
Let the equation of the parabola
y² = 4ax ……………. (1)
and P(at², 2at) be any point
Ordinate – abscissa
= 2at = at² = t=0 or t = 2
But t ≠ 0, Hence the point (4a, 4a) at which normal is
⇒  y + 2x = 2a(2) + a(2)³
⇒  y + 2x = 4a + 8a
⇒  y=12a -2x …………….. (2)
∴ From (1) we get
(12a – 2x)² – 4ax
⇒ 4x² – 48ax + 144a² = 4ax
⇒ 4x² – 52ax+ 144a²= 0
⇒ x² – 13ax + 36a² = 0
⇒ (x – 4a) (x – 9a) – 0
⇒ x = 4a, 9a
Correspondingly we get y = 12a – 8a = 4a and y = 12a – 18a= – 6a
Hence the other points of intersection of normal at P(4a, 4a) is Q(9a – 6a).
We have S = (a, 0)

Question 6.
Prove that the area of the triangle formed by the tangents at (x₁, y₁), (x₂, y₂) and (x₃,y₃) to the parabola y² = 4ax
\(\frac{1}{16 a}\left|\left(y_1-y_2\right)\left(y_2-y_3\right)\left(y_3-y_1\right)\right|\)  sq. unit
Solution:
Let A (x₁, y₁) = (at₂², 2at₁)
B (x₂, y₂) =  (at₂², 2at₂)
C (x₃, y₃) – (at₃², 2at₃) be the three points on the parabola y²=4ax.
The equations of tangents at A, B, C are

∴ Point of intersection of tangents at A and B is P(at₁t₂, a(t₁ + t₂)).
Similarly the points of intersection of tangents at B and C as well as A & C are

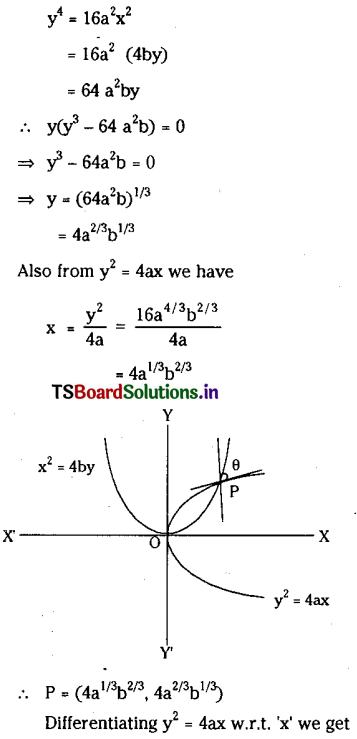
Question 7.
Prove that the two parabolas y² = 4ax and x² = 4by intersect other than the origin) at tan^-1
\(\left(\frac{3 a^{1 / 3} b^{1 / 3}}{2\left(a^{2 / 3}+b^{2 / 3}\right)}\right)\)
Solution:
Take a>0, b>0
and y²=4ax ………………….. (1)
and x² = 4by are ……………. (2)
the given parabolas.
Solving (1) and (2) we get the point of intersection other than the origin.

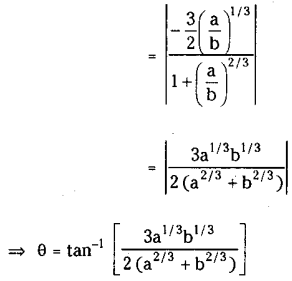
Question 8.
Prove that the orthocentre of the triangle formed by any three tangents to a parabola lies on the directrix of the parabola.
Solution:
Let y² = 4ax be the parabota and
A = (at₁², 2at₁), B = (at₂², 2at₂),
C = (at₃², 2at₃) be any three points on It.
If P, Q, R are the points of intersection of tangents at A and B, B and C, C and A then
P = [at₁t₂, a(t₁ + t₂)] Q = [at₂t₃, a(t₂ + t₃)] R = [at₁t₃, a(t₁ + t₃)]
Consider the ΔPQR then equation \(\overline{\mathrm{QR}}\) of (Tangent at C) is
x – yt₃ + at₃² = 0
∴ Altitude through P of Δ PQR is
t₃x + y = at₁t₂t₃ + a(t₁ + t₂) …………….. (1)
∴ Slope = \(\frac{1}{t_3}\) and equation is
y – a(t₁+ t₂) = – t₃ [x – at₁t₂]
y+xt₃ – at₁t₂t₃+a(t₁ +t₂)
Similarly the altitude through Q is
t₁x + y – at₁t₂t₃ + a(t₂+ t) …………… (2)
Solving (1) and (2)
x(t₃ – t₁) = a(t₁– t)
⇒ x = – a
Hence the orthocentre of ΔPQR with x coordinate as – ‘a’ lies on the directrix of the parabola.