TS Inter 2nd Year Maths 2B Definite Integrals Important Questions

Students must practice these TS Inter 2nd Year Maths 2B Important Questions Chapter 7 Definite Integrals to help strengthen their preparations for exams.

TS Inter 2nd Year Maths 2B Definite Integrals Important Questions

Very Short Answer Type Questions

Question 1.
Evaluate \(\int_1^2 x^5\) dx
Solution:
\(\int_1^2 x^5 d x=\left[\frac{x^6}{6}\right]_1^2=\frac{2^6}{6}-\frac{1}{6}=\frac{64}{6}-\frac{1}{6}=\frac{63}{6}=\frac{21}{2}\)

Question 2.
Evaluate \(\int_0^\pi \) sinx dx
Solution:

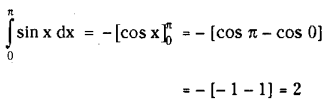
Question 3.
Evaluate \(\int_0^a \frac{d x}{x^2+a^2}\)
Solution:

Question 4.
Evaluate \(\int_1^4 x \sqrt{x^2-1}\) dx
Solution:
Let x² – 1 – t ⇒ 2x dx dt then
Upper limit when x = 4 is t = 15.
Lower Limit when x = 1 is t = 0.

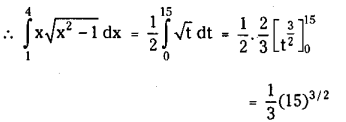
Question 5.
Evaluate \(\int_0^2 \sqrt{4-x^2}\) dx
Solution:
Let x= 2 sin θ = dx – 2cosθ dθ then

Question 6.
Show that \(\int_0^{\frac{\pi}{2}} \sin ^n x d x=\int_0^{\frac{\pi}{2}} \cos ^n x dx\)
Solution:

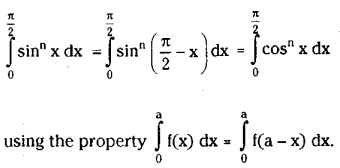
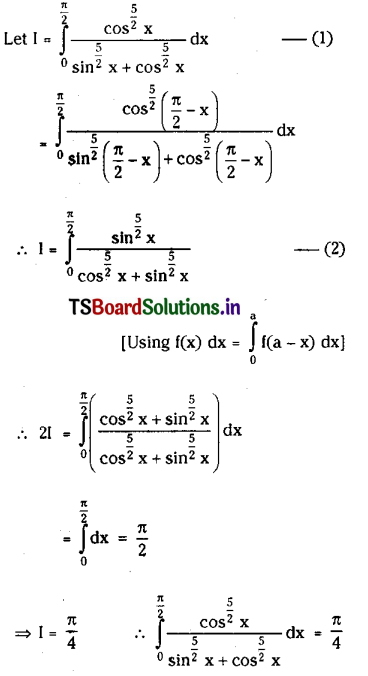
Question 7.
Evaluate \(\int_0^{\frac{\pi}{2}} \frac{\cos ^{\frac{5}{2}} x}{\sin ^{\frac{5}{2}} x+\cos ^{\frac{5}{2}} x}\) dx
Solution:

Question 8.
Evaluate \(\int_0^{\frac{\pi}{2}} \) x sin x dx
Solution:

Question 9.
Evaluate

Solution:

(iii) \(\int_0^{\frac{\pi}{2}} \sin ^6 x \cos ^4 x dx\)
Solution:

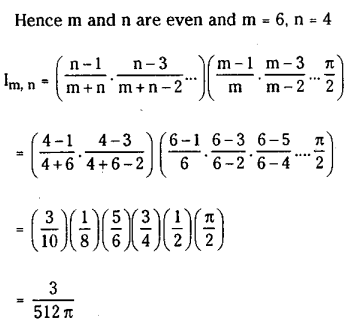
Question 10.
Find \(\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \sin ^2 x \cos ^4 x d x\)
Solution:

Short Answer Type Questions

Question 1.
Find \(\int_0^2\left(x^2+1\right) dx\) as the limit of a sum
Solution:

Question 2.
Evaluate \(\int_0^2 e^x dx\) as the limit of a sum.
Solution:

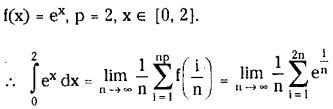
Question 3.
Lets define f : [0,1]→ R by
f(x) = 1 if x is rational
= 0 if x is irrational
then show that f is nor R Integrable over [0, 1].
Solution:
Let P = (x₀, x₁,…., x_n] be a partition of [0, 1].
Since between any two real numbers there exists rational and irrational numbers and
let t_i, s_i ∈ [X_i -i x_j] be the rational and irrational numbers.

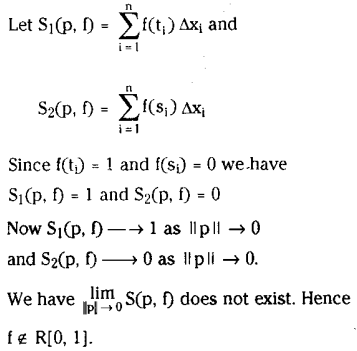
Question 4.
Evalute \(\int_0^{16} \frac{x^{\frac{1}{4}}}{1+x^{\frac{1}{2}}}\) dx
Solution:
Let x = t⁴ then dx – 4t³ dt
Upper limit when x = 16 is t = 2.
and Lower limit when x = 0 is t = 0.

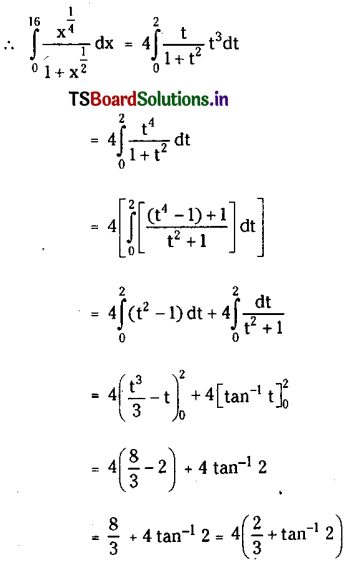
Question 5.
Evaluate \(\int_{-\frac{\pi}{2}}^\pi \sin\) |x| dx
Solution:
We have sin |x| = sin(-x) if x < 0
= sinx if x ≥ 0

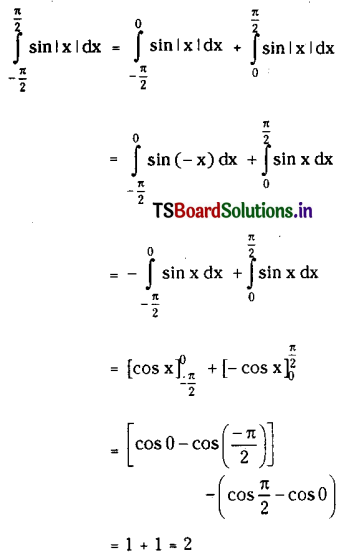
Question 6.
Evaluate by using the method of finding definite integral as the limit of a sum.
\(\lim _{n \rightarrow \infty} \sum_{i=1}^n \frac{1}{n}\left(\frac{n-1}{n+1}\right)\)
Solution:

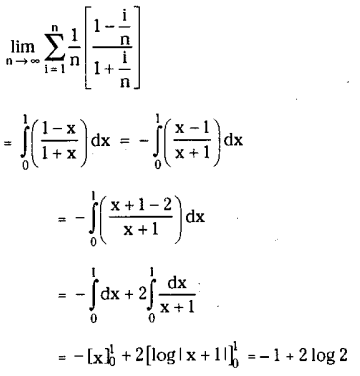
Question 7.
Evaluate \(\lim _{n \rightarrow \infty} \frac{2^k+4^k+6^k+\ldots+(2 n)^k}{n^{k+1}}\) using the method of finding definite integral as the limit of a sum.
Solution:

Question 8.
Evaluate \(\lim _{n \rightarrow \infty}\left[\left(1+\frac{1}{n}\right)\left(1+\frac{2}{n}\right) \ldots\left(1+\frac{n}{n}\right)\right]^{\frac{1}{n}}\)
Solution:

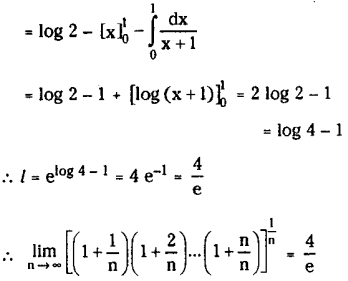
Question 9.
Obtain Reduction formula for \(\int_0^{\frac{\pi}{2}} \sin ^n x d x\) and hence find

Solution:

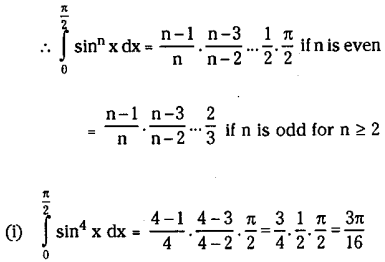
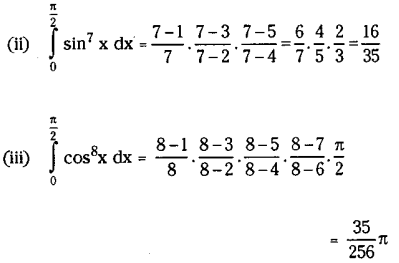
Question 10.
Evaluate \(\int_0^a \sqrt{a^2-x^2} dx\)
Solution:
Let x = a sinθ then dx = a cosθ dθ
Upper limit when x = a is θ = \(\frac{\pi}{2}\)
and Lower limit when x = 0 is θ = 0

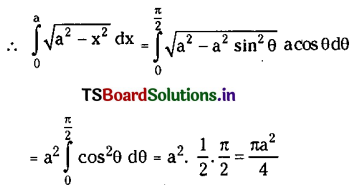
Question 11.
Find \(\int_{-a}^a x^2\left(a^2-x^2\right)^{3 / 2} dx\)
Solution:
Since f(x) = x² (a² – x²)^3/2 is an even function and f(- x) = f(x) we have
\(\int_{-a}^a x^2\left(a^2-x^2\right)^{3 / 2} d x=2 \int_0^a x^2\left(a^2-x^2\right)^{3 / 2} d x\)
Let x = a sin θ then dx = a cos θ dθ
∴ Upper limit when x = a is θ = \(\frac{\pi}{2}\)
Lower limit when x = 0 is θ = 0

Question 12.
Find \(\int_0^1 x^{3 / 2} \sqrt{1-x} dx\)
Solution:
Let x = sin²θ then dx = 2 sinθ cosθ dθ
Upper limit when x = 1 is θ = \(\frac{\pi}{2}\)
Lower Limit when x = θ is θ = 0.

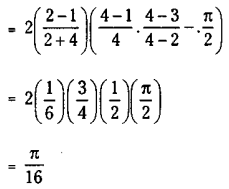
Question 13.
Find the area under the curve f(x) = sin x in (0, 2π).
Solution:
Consider the graph of the function f(x) = sinx in [0, 2π];
we have sin x ≥ 0 ∀ x ∈ [0,π] and sin x≤0∀x∈[π,2π].

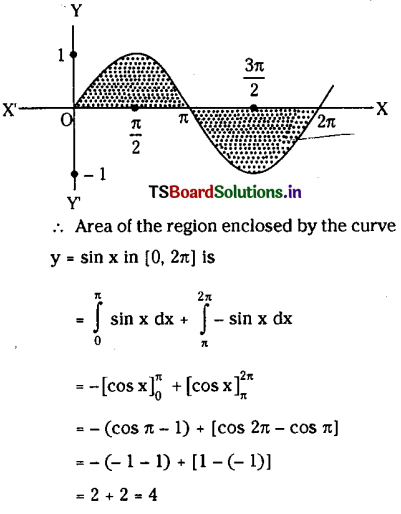
Question 14.
Find the area under the curve f(x) = cos x in [0, 2π].
Solution:

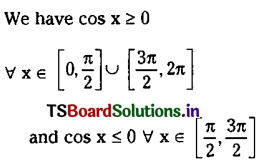
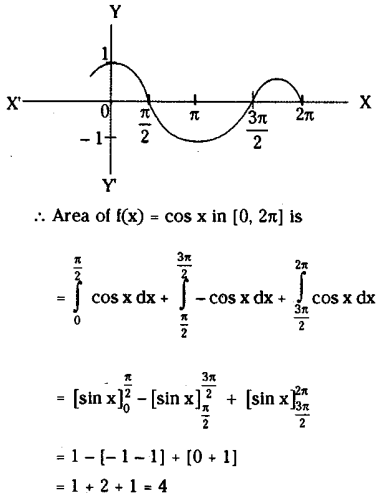
Question 15.
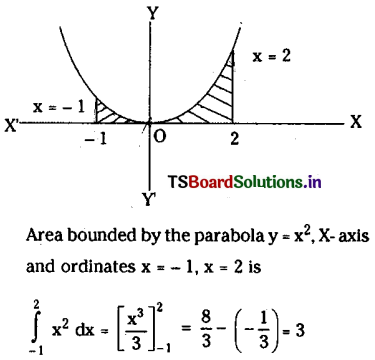
Find the bounded by the y = x² parabola the X- axis and the lines x = – 1, x = 2.
Solution:

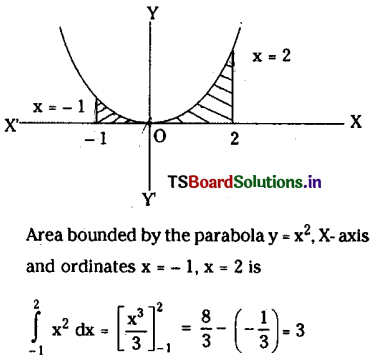
Question 16.
Find the area cut off between the line y = 0 and the parabola y = x²– 4x + 3.
Solution:
The point of intersection of y – 0 and y = x² – 4x + 3 is given by x² – 4x + 3 = 0
= (x – 3)(x-1) = 0 = x = 1 or 3
y=x²– 4x + 3 ⇒ y+1 =  x²– 4x + 4 (x-2)²
Hence the equation represents a parabola
with vertex (2, -1) lies in IV quadrant.

Question 17.
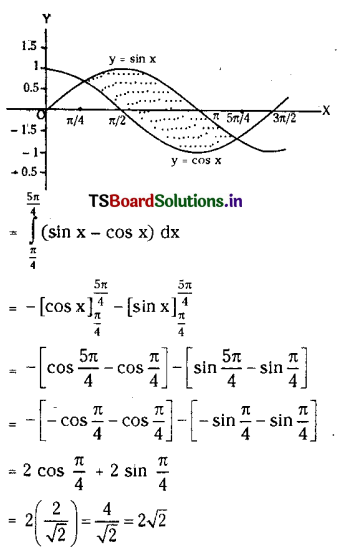
Find the area bounded by the curves y = sin x and y = cos x between any two consecutive points of intersection.
Solution:
The given curves y = sin x and y = cosx and
tan x = 1 ⇒ x = \(\frac{\pi}{4}\)
∴ x = \(\frac{\pi}{4}\) and x = \(\frac{5 \pi}{4}\) are the two consecutive points of intersection.
Taking f(x) = sin x and g(x) cos x over \(\left[\frac{\pi}{4}, \frac{5 \pi}{4}\right]\) we have
f(x)> g(x) ∀ x ∈\(\left[\frac{\pi}{4}, \frac{5 \pi}{4}\right]\).
Hence the area bounded by y = sin x, y = cos x and the two points of intersection is

Question 18.
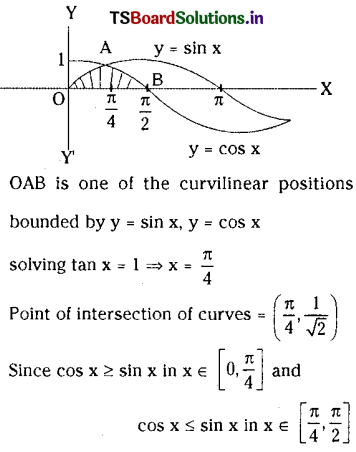
Find the area of one of the curvilinear rectangles bounded by y = sin x, y cos x and X-axis.
Solution:

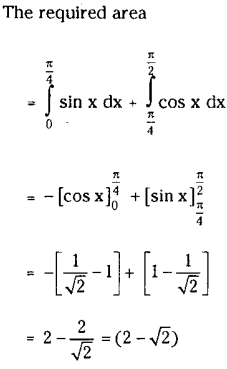
Question 19.
Find the area of the right angled triangle with base b and altitude ‘h’ using the fundamental theorem of integral calculus.
Solution:

Question 20.
Find the area bounded between the curves y² – 1 = 2x and x = 0.
Solution:
The given curves are
y²-1-2x-2(x-0) ……………. (1)
= (y-0)² 2(x)+1=2 \(\left[\mathrm{x}+\frac{1}{2}\right]\)
(1) represents parabola with vertex \(\left(-\frac{1}{2}, 0\right)\)
Solving (1) and x = 0 we get
y² -1 = 0 ⇒ y = ±1
∴ The points of intersection are (0, 1), (0, -1).
The parabola meets the X- axis and y = 1 and y = – 1 and the curve is symmetric with respect to X – axis

Question 21.
Find the area enclosed by the curves y = 3x and y = 6x-x².
Solution:
Given curves are y³x and y=6x – x²
Solving 6x – x² = 3x = 3x – x² = 0
= x(3- x)=0 =x=0 or x=3
Taking f(x) = 3x and g(x) = 6x – x²
then g(x) ≥ 1(x) in [0, 3] and area enclosed between the line y = 3x and the parabola y = 6x-x² is

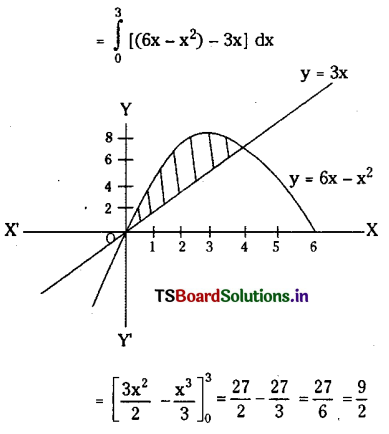
Long Answer Type Questions

Question 1.
Show that \(\int_0^{\frac{\pi}{2}} \frac{x}{\sin x+\cos x}\) dx =\(\frac{\pi}{2 \sqrt{2}} \log (\sqrt{2}+1)\)
Solution:

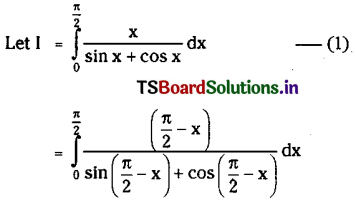
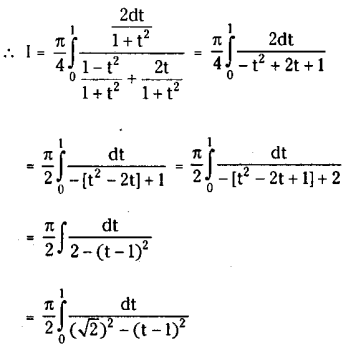
Question 2.
Evaluate \(\int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \frac{\sqrt{\sin x}}{\sqrt{\sin x}+\sqrt{\cos x}}\) dx
Solution:

Question 3.
Evaluate \(\int_{-a}^a\left(x^2+\sqrt{a^2-x^2}\right) dx\)
Solution:

Question 4.
Evaluate \(\int_0^\pi \frac{x \sin x}{1+\sin x}\) dx
Solution:

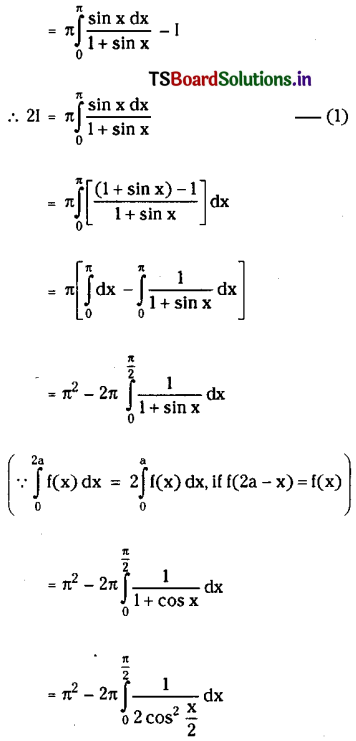
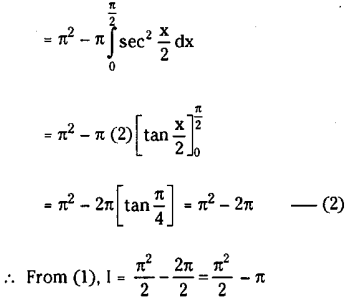
Question 5.
Find \(\int_0^\pi \mathbf{x}\) sin⁷ x cos ⁶ x dx.
Solution:

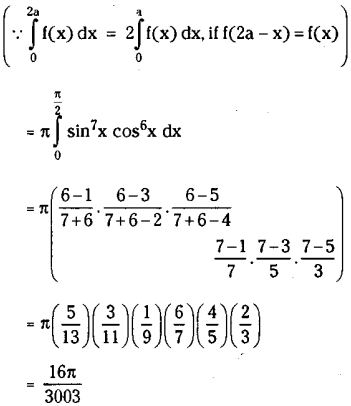
Question 6.
Find the area enclosed between y=x²-5x and y=4-2x.
Solution:
The graphs of curves are shown below.

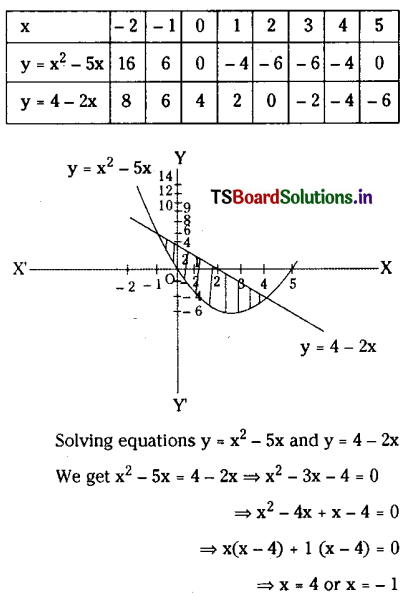
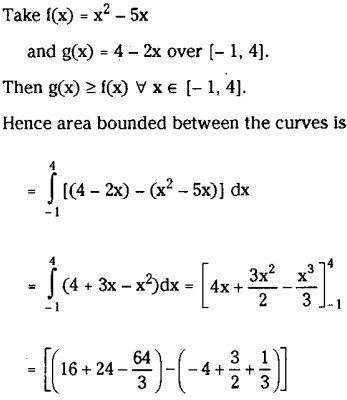
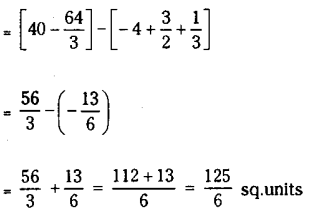
Question 7.
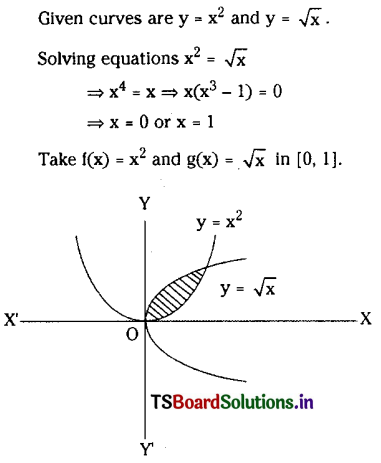
Find the area bounded between the curves y = x², y = \(\sqrt{\mathbf{x}} \)
Solution:

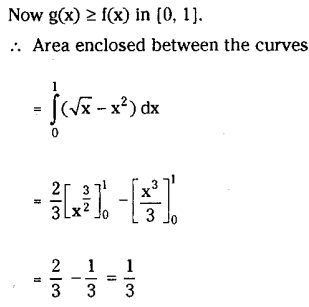
Question 8.
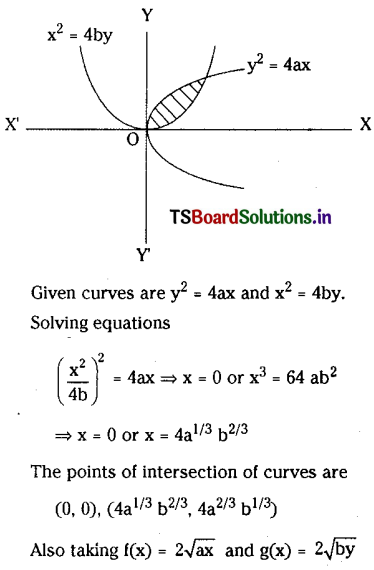
Find the area bounded between the curves y²=4ax, x²= 4by(a>0,b>0).
Solution: