TS Inter 1st Year Physics Study Material Chapter 2 ప్రమాణాలు, కొలత

Telangana TSBIE TS Inter 1st Year Physics Study Material 2nd Lesson ప్రమాణాలు, కొలత Textbook Questions and Answers.

TS Inter 1st Year Physics Study Material 2nd Lesson ప్రమాణాలు, కొలత

అతిస్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
యథార్థత, ఖచ్చితత్వాల మధ్య తేడాను రాయండి.
జవాబు:
యథార్థత (Accuracy) : మనం కొలిచిన విలువ మనం కొలవవలసిన భౌతికరాశి నిజమైన విలువకు ఎంత దగ్గరగా ఉన్నదో తెలియజేయు కొలమానాన్ని యథార్థత అంటారు.

ఖచ్చితత్వము (Precision) : ఖచ్చితత్వము అనేది మనం ఒక పరికరంతో ఎంత కనిష్ఠ అవధి వరకు ఇచ్చిన భౌతికరాశిని కొలవగలమో తెలియజేస్తుంది.
మనం కొలవగలిగిన కనిష్ఠ అవధి ఎంత తక్కువ ఐతే ఆ పరికరం ఖచ్చితత్వం అంత ఎక్కువ.

ప్రశ్న 2.
కొలతలో వచ్చే వివిధ రకాల దోషాలు ఏవి ?
జవాబు:
భౌతిక రాశుల కొలతలలో సంభవించగల దోషాలు రెండు రకాలు.

1. క్రమదోషాలు,
2. యాదృచ్ఛిక దోషాలు.

క్రమదోషాలను మరల 1) స్థిర దోషాలు, 2) వ్యక్తిగత దోషాలు, 3) పరిసర సంబంధిత దోషాలు, 4) ప్రయోగ విధాన కౌశలం లేక ప్రయోగ పద్ధతిలోని అసమగ్రత వలన కలుగు దోషాలుగా విభజించినారు.

ప్రశ్న 3.
క్రమదోషాలను ఏ విధంగా కనిష్ఠం చేయవచ్చు లేదా తొలగించవచ్చు ? (మార్చి 2014)
జవాబు:
1) ప్రయోగ టెక్నిక్లలను మెరుగుపరచుకొని, 2) శ్రేష్ఠమైన పరికరాలను వాడి, 3) అనేక రీడింగులను తీసుకొని కొలతలో సంభవించగల క్రమదోషాలను అంచనా వేసి తగిన సవరణ చేయడం వల్ల క్రమదోషాలను తగ్గించవచ్చు.

ప్రశ్న 4.
కొలత ఫలితాన్ని అందులో ఉండే దోషాన్ని సూచిస్తూ ఏ విధంగా నివేదిస్తారో ఉదాహరణలతో వివరించండి.
జవాబు:
కొలతల ఫలితాలను నివేదించే పద్ధతి : సాధారణ మీటరు స్కేలుతో 1 మి.మీ. వరకు కొలత ఖచ్చితంగా కొలవగలము. ఇటువంటి స్కేలుతో ఒక కడ్డీ పొడవు 62.5 సెం.మీ. అని కొలిచామనుకోండి. ఈ కొలతను 62.5 ± 0.1 అని చూపాలి. అంటే మన కొలత 0.1 సెం.మీ. లేదా 1 మి.మీ. వరకు ఖచ్చితమైనది అని తెలుపుతుంది.

ఇదే విధంగా లఘులోలకం ప్రయోగంలో డోలనావర్తన కాలము 2 సెకనులుగా కొలిస్తే దానిని 2.0 ± 0.1 గా చూపితే ఇందులో 0.1 మనం వాడిన ఆపు గడియారం కనీసపు కొలతను సూచిస్తూ మన ప్రయోగ విలువ మొదటి దశాంశము వరకు నమ్మదగినది అని తెలుపుతుంది.

ప్రశ్న 5.
సార్థక సంఖ్యలంటే ఏవి ? ఒక కొలత ఫలితాన్ని నివేదించేటప్పుడు అవి ఏమి సూచిస్తాయి ?
జవాబు:
ప్రయోగంలో నమోదు చేసిన కొలతల ఫలితం ఒక సంఖ్య. ఈ సంఖ్యలో మనం ప్రయోగం ద్వారా పొందిన నమ్మదగిన అంకెలతో పాటు అనిశ్చితత్వాన్ని తెలియజేసే మరొక సంఖ్యను కూడా కలిపి సార్థక సంఖ్యలు అంటారు.

ప్రయోగ ఫలితంలో సార్థక సంఖ్యల కన్నా ఎక్కువ అంకెల వల్ల ప్రయోజనం లేకపోగా అవి ఖచ్చితత్వానికి సంబంధించి తప్పుడు అభిప్రాయం కలుగచేస్తాయి.

ప్రశ్న 6.
ప్రాథమిక ప్రమాణాలు, ఉత్పన్న ప్రమాణాల మధ్య తేడాలు రాయండి. (మే 2014)
జవాబు:
ప్రాథమిక లేక మూల రాశులను కొలిచే ప్రమాణాలు ప్రాథమిక ప్రమాణాలు.
ఉదా : పొడవు – మీటరు, ద్రవ్యరాశి → కి.గ్రా.
ఉత్పన్న రాశులను కొలిచే ప్రమాణాలను ఉత్పన్న ప్రమాణాలు అంటారు. ఉత్పన్న ప్రమాణాలు ప్రాథమిక ప్రమాణాల కలయిక వల్ల ఏర్పడతాయి. ఉదా : వేగము మీటరు / సెకను

ప్రశ్న 7.
ఒకే భౌతికరాశికి వేరువేరు ప్రమాణాలు ఎందుకు ఉంటాయి ?
జవాబు:
భౌతిక రాశుల పరిమాణము అత్యల్ప విలువల నుండి అత్యధిక విలువల వరకు విస్తృత పరిధిలో మారే అవకాశం ఉండటం వల్ల ఒక రాశిని ఖచ్చితంగా కొలవడానికి వేరు వేరు ప్రమాణాలు అవసరమవుతాయి.

ఉదా : పరమాణువుల మధ్య దూరాన్ని కొలవడానికి ఆంగ్జామ్ యూనిట్ను వాడతారు. 1 Å = 10^-8 m. సుదూర నక్షత్రాల మధ్య దూరాలను కొలవడానికి కాంతి సంవత్సరాన్ని ప్రమాణంగా వాడతారు.

ప్రశ్న 8.
మితీయ విశ్లేషణ అంటే ఏమిటి ?
జవాబు:
భౌతిక రాశుల మధ్య ప్రవర్తన వివరించడానికి (1) ఒకే మితులు కలిగిన భౌతిక రాశులను కలపడం లేదా వ్యవకలనం చేయడం జరుగుతుంది. (2) భౌతిక రాశుల మధ్య నిర్దిష్ట సంబంధాలు రాబట్టడానికి, ఆ సమీకరణాల యథార్థత పరిశీలించడానికి మితుల ఆధారంగా ఉపయోగించే పద్ధతులను మితి విశ్లేషణ అంటారు.

ప్రశ్న 9.
కేంద్రకం వ్యాసార్ధంతో పోలిస్తే పరమాణు వ్యాసార్ధం పరిమాణ క్రమాలలో ఎంత ఎక్కువగా ఉంటుంది ?
జవాబు:
పరమాణు పరిమాణము 10^-10 m స్థాయిలో ఉంటుంది.
కేంద్రక పరిమాణము 10^-14 m స్థాయిలో ఉంటుంది.
కావున పరమాణు పరిమాణము, కేంద్రక పరిమాణ క్రమాల విలువ 10^-10 ÷ 10^-14 = 10⁴.
అనగా పరమాణు పరిమాణం, కేంద్రక పరిమాణము కన్నా సుమారు 10⁴ రెట్లు ఎక్కువ.

ప్రశ్న 10.
ఏకీకృత పరమాణు ద్రవ్యరాశి ప్రమాణాన్ని కి.గ్రా.లో వ్యక్తం చేయండి.
జవాబు:
ఏకీకృత పరమాణు ప్రమాణము (1 a.m.u.) కర్బన ఐసోటోపు ఐన \({ }_6^{12} \mathrm{C}\) పరమాణు ద్రవ్యరాశిలో \(\frac{1}{12}\)వ సమానము.
1 a.m.u. = \(\frac{1}{12}\) \({ }_6^{12} \mathrm{C}\) = 1.66 × 10^-27 కి.గ్రా.

స్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
ఒక పరికరం వెర్నియర్ స్కేలు 50 విభాగాలు కలిగి ఉంది. ఇవి ప్రధాన స్కేలుపై ఉండే 49 విభాగాలతో ఏకీభవిస్తాయి. ప్రధాన స్కేలులోని ప్రతి విభాగం విలువ 0.5 mm. అయితే ఈ పరికరంతో కొలిచే దూరంలో కనిష్ఠ యథార్థతారాహిత్యం ఎంత ఉంటుంది ?
జవాబు:
వెర్నియర్ కాలిపర్స్ కొలవగల కనీస కొలత L.C. = \(\frac{\mathrm{S}}{\mathrm{N}}\)
ప్రధాన స్కేలు విభాగాల మధ్య దూరము S = 0.5 మి.మీ.
వెర్నియర్ స్కేలు విభాగాల సంఖ్య N = 50
∴ వెర్నియర్ కాలిపర్స్ కనీస కొలత L.C. = \(\frac{\mathrm{S}}{\mathrm{N}}=\frac{0.5}{50}=\frac{0.1}{10}=\frac{1}{100}\) మి.మీ.

ప్రశ్న 2.
ప్రమాణాల ఒక వ్యవస్థలో బలానికి ప్రమాణం 100 N, పొడవుకు ప్రమాణం 10m, కాలానికి ప్రమాణం 100s. ఈ వ్యవస్థలో ద్రవ్యరాశికి ఉండే ప్రమాణం ఏది ?
జవాబు:
బలము (F) కు మితి ఫార్ములా F = MLT^-2 → 1
బల ప్రమాణము F = 100 N, పొడవు L = 10 మీ., కాలము T = 100 సె.
1వ సమీకరణము నుండి M = \(\frac{\mathrm{F}}{\mathrm{LT}^{-2}}\)
ద్రవ్యరాశి ప్రమాణము = \(=\frac{\mathrm{F}}{\mathrm{LT}^{-2}}\) = 10⁵ కి. గ్రా.

ప్రశ్న 3.
భూమి నుంచి ఒక గెలాక్సీ దూరం 10²⁵ m ల క్రమంలో ఉంది. గెలాక్సీ నుంచి కాంతి మనల్ని చేరేందుకు పట్టే కాలం పరిమాణక్రమాన్ని గణించండి.
జవాబు:
గెలాక్సీ దూరము d = 10²⁵ మీ., కాంతివేగము C = 3 × 10⁸ మీ/సె
కాంతి ప్రయాణించిన కాలము t = \(\frac{\mathrm{d}}{\mathrm{c}}=\frac{10^{25}}{3 \times 10^8}=\frac{1}{3}\) × 10¹⁷ = 0.333 × 10¹⁷ సెకనులు
కాలం క్రమం నిర్ణయించడంలో ’10’ యొక్క ఘాతం విలువ మాత్రమే లెక్కలోనికి తీసుకుంటారు.
∴ కాలం పరిమాణక్రమం = 10¹⁷.

ప్రశ్న 4.
భూమి-చంద్రుల మధ్య దూరం భూవ్యాసార్ధానికి సుమారు 60 రెట్లు. చంద్రుడి నుంచి చూస్తే భూమి వ్యాసం సుమారుగా ఎంత ఉంటుంది ?
జవాబు:
భూమి, చంద్రుల మధ్య దూరము D = 60 × భూమి వ్యాసార్ధము = 60r
భూమి వ్యాసము D = 2r

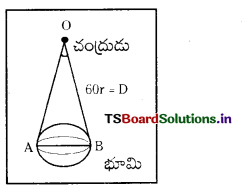
చంద్రుని నుంచి చూసినపుడు పారలాక్టిక్ కోణము θ =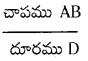
∴ చంద్రుని పరిమాణము = \(\frac{2 \mathrm{r}}{60 \mathrm{r}}=\frac{1}{30}\) రేడియన్ లేదా θ \(\frac{57^{\circ} 30^{\prime}}{30}\) ≃ 2°

ప్రశ్న 5.
లోలకం 20 డోలనాలకు పట్టే కాలానికి వచ్చిన మూడు కొలతలు వరుసగా t₁ = 39.6s, t₂ = 39.9s, t₃ = 39.5s. కొలతల్లోని ఖచ్చితత్వం ఎంత ? కొలతల్లోని యథార్థత ఎంత ?
జవాబు:
ఖచ్చితత్వము పరికరం కనీస కొలతపై ఆధారపడుతుంది. ఈ సందర్భంలో ఖచ్చితత్వము ± 0.1 సెకను. ఎందుకనగా కొలతలలోని చివరి అంకెలో మాత్రమే అనిశ్చితత్వం ఉంటుంది.
కొలతలలోని యథార్థత :
కొలతల సగటు విలువ = \(\frac{39.6+39.9+39.5}{3}=\frac{119}{3}\) = 39.67
ప్రతి కొలతలో దోషము ∆a₁ = 39.67 – 39.6 = 0.07
∆a₂ = 39.9 – 39.67 = 0.23
∆a₃ = 39.67 – 39.5= 0.17
∆а_సగటు = \(\frac{0.07+0.23+0.17}{3}\) = 0.156
∆а_సగటు ను సార్థక సంఖ్యల వరకు సవరించగా = 0.156 ను 0.2 గా సవరించినాము.
±0.2 కొలతలోని యథార్థత.
పరిశీలనల యథార్థత 39.67 ± 0.2, దీనిని సార్థక సంఖ్యలకు సవరించగా 39.7 ± 0.2 సెకనులు.

ప్రశ్న 6.
1 కెలోరి = 4.2J, 1J = 1 kg m²s². ద్రవ్యరాశికి ప్రమాణం α kg గా, పొడవుకు ప్రమాణం βm గా, కాలం ప్రమాణం γs గా ఉండే ఒక ప్రమాణ వ్యవస్థను వాడినపుడు, కొత్త వ్యవస్థలో కెలోరికి ఉండే పరిమాణం 4.2 α^-1 β² γ² అని చూపండి.
జవాబు:
1 కెలోరి = 4.2 J
= 4.2 kg m² / s² → (1); ద్రవ్యరాశి నూతన ప్రమాణం= α kg
∴ 1 kg = \(\frac{1}{\alpha}\) కొత్త ప్రమాణాలు = α^-1 కొత్త ప్రమాణము
ఇదే విధంగా మీటరు కొత్త ప్రమాణము 1 m = β^-1; కాలము కొత్త ప్రమాణము 1s = γ^-1
ఈ విలువలు సమీకరణం (1) లో రాయగా
1 కెలోరి = 4.2 (α^-1) (β^-1)² (γ^-1)^-2
శక్తి నూతన ప్రమాణము = 4.2 α^-1β^-2γ²

ప్రశ్న 7.
శూన్యంలో కాంతి వడి 1 ms^-2 అయ్యేవిధంగా పొడవుకు ఒక కొత్త ప్రమాణాన్ని ఎంచుకొన్నారు. సూర్యుడి నుంచి కాంతి భూమిని చేరేందుకు పట్టే కాలం 8 నిమిషాల 20 సెకన్లయితే కొత్త ప్రమాణాల్లో సూర్యుడు – భూమి మధ్య దూరం ఎంత ?
జవాబు:
శూన్యంలో కాంతి వడికి కొత్త ప్రమాణము C = 1 N.U./Sec.
కాంతి భూమిని చేరడానికి పట్టిన కాలము t = 8 ని. 20 సె.
= (8 × 60) + 20 = 500 సె
సూర్యుని నుంచి భూమి దూరము X = C × t
= 1 N.U. × 500 = 500 కొత్త ప్రమాణాలు

ప్రశ్న 8.
100 ఆవర్ధనం ఉండే సూక్ష్మదర్శినిని ఉపయోగించి ఒక విద్యార్థి మానవుడి వెంట్రుక మందాన్ని కొలుస్తున్నాడు. 20 పరిశీలనల వల్ల వెంట్రుకల సగటు మందాన్ని (సూక్ష్మదర్శినిలో చూసినదాని దృష్ట్యా) 3.5 mm గా కనుక్కొన్నాడు. అంచనాకు వచ్చే మందం ఎంత ?
జవాబు:

ప్రశ్న 9.
కొలవగలిగే నాలుగు రాశులు a, b, c, d లతో X అనే భౌతిక రాశి కింది విధంగా సంబంధాన్ని కలిగి ఉంది. X = a²b³ c^5/2 d^-2. a, b, c, d లను కొలవడంలో దోష శాతాలు వరుసగా 1%, 2%, 3%, 4% అయితే X లో దోషశాతం ఎంత ?
జవాబు:
దత్తాంశము X = a²b³ c^5/2 d^-2
\(\frac{\Delta \mathrm{a}}{\mathrm{a}}\) × 100 = 1%, \(\frac{\Delta \mathrm{b}}{\mathrm{b}}\) × 100 = 2%; \(\frac{\Delta \mathrm{c}}{\mathrm{c}}\) × 100 = 3%, \(\frac{\Delta \mathrm{d}}{\mathrm{d}}\) × 100 = 4%
\(\frac{\Delta \mathrm{X}}{\mathrm{X}}=\pm\left[2\left(\frac{\Delta \mathrm{a}}{\mathrm{a}}\right)+3\left(\frac{\Delta \mathrm{b}}{\mathrm{b}}\right)+\frac{5}{2}\left(\frac{\Delta \mathrm{c}}{\mathrm{c}}\right)+2\left(\frac{\Delta \mathrm{d}}{\mathrm{d}}\right)\right]\)
= ±[2(1%) + 3(2%) + \(\frac{5}{2}\) (3%) + 2(4%)] = ± 23.5%
‘X’ లో దోషశాతము = ± 23.5%

ప్రశ్న 10.
ఒక వస్తువు వేగం v = At² + Bt + C అని ఇవ్వడమైంది. v, t లను SI ప్రమాణాల్లో వ్యక్తం చేస్తే A, B, C లకు ప్రమాణాలు రాయండి.
జవాబు:
మితుల సజాతీయతను అనుసరించి At², Bt మరియు C ల మితి ఫార్ములాల వేగము ‘v’ మితి ఫార్ములాకు సమానము.
∴ V = వేగము = LT^-1
∴ LT^-1 = A [T²], ∴ A = \(\frac{\mathrm{LT}^{-1}}{\mathrm{~T}^2}\) = LT³. కావున A ప్రమాణము మీ/సె³
LT^-1 = BT ⇒ B = LT^-2 కావున B ప్రమాణము మీ/సె²
LT^-1 = C కావున C ప్రమాణము మీ/సె.

లెక్కలు

ప్రశ్న 1.
P = E l² m^-5 G^-2 అనే సమాసంలో E, l, m, G లు వరుసగా శక్తి, కోణీయ ద్రవ్యవేగం, ద్రవ్యరాశి, గురుత్వ స్థిరాంకాలను సూచిస్తే P ఒక మితిరహిత రాశి అని చూపండి.
సాధన:
దత్తాంశము, P = El²m^-5G^-2
= [M L²T^-2][M L²T^-1]² [M]^-5 [M^-1L³T^-2]^-2
= M^1+2-5+2 L^2+4-6 T^-2-2+4 = [M⁰ L⁰ T⁰]
P = [M⁰ L⁰ T⁰] అనగా P మితులు లేని రాశి.

ప్రశ్న 2.
కాంతివేగం C, ప్లాంక్ స్థిరాంకం h, విశ్వగురుత్వ స్థిరాంకం G లను ప్రాథమిక రాశులుగా తీసుకొంటే, ఈ రాశుల మితుల్లో ద్రవ్యరాశి, పొడవు, కాలాలను రాయండి.
సాధన:
దత్తాంశము నుండి c = [LT^-1]; h = [ML²T^-1]; G = [M^-1L³T^-2]
m = c^xh^yG^z → (1)
⇒ [M¹L⁰T⁰] = (LT^-1)^x (M L²T^-1)^y (M^-1L³T^-2)^z
⇒ [M¹L⁰T⁰] = M^y-zL^x+2y+2z T^-x-y-2z
సదిశల సజాతీయతా నియమం నుండి
y – z = 1 → (2)
x + 2y + 3z = 0 → (3)
-x – y – 2z = 0 → (4)
సమీకరణములు (2), (3), (4) లను కలుపగా
2y = 1 ⇒ y = \(\frac{1}{2}\)
సమీ. (2) నుండి z = y – 1 = \(\frac{1}{2}\) – 1 = \(\frac{-1}{2}\)
సమీ. (4) నుండి x = -y – 2z = \(\frac{-1}{2}\) + 1 = \(\frac{1}{2}\)
x, y మరియు Z విలువలు సమీ. (1) లో రాయగా
m = c^{\(\frac{1}{2}\)} h^{\(\frac{1}{2}\)} G^{\(\frac{-1}{2}\)} ;
⇒ m = \(\sqrt{\frac{\mathrm{ch}}{\mathrm{G}}}\)
m ను కనుక్కునే విధంగా సమీకరణాలు సాధిస్తే
L = \(\sqrt{\frac{\mathrm{hG}}{\mathrm{c}^3}}\) మరియు T = \(\sqrt{\frac{\mathrm{hG}}{\mathrm{c}^5}}\) అను సమీకరణాలు వస్తాయి.

ప్రశ్న 3.
M ద్రవ్యరాశి, R వ్యాసార్ధం కలిగి ఉండే గ్రహం చుట్టూ వ్యాసార్ధం ఉన్న వృత్తాకార కక్ష్యలో ఒక కృత్రిమ ఉపగ్రహం పరిభ్రమిస్తుంది. మితీయ విశ్లేషణ ఆధారంగా ఉపగ్రహ కక్ష్యావర్తన కాలం
T = \(\frac{k}{R} \sqrt{\frac{\mathrm{r}^3}{\mathrm{g}}}\) అని చూపండి. ఇక్కడ k మితిరహిత స్థిరాంకం, g గురుత్వ త్వరణం.
సాధన:
దత్తాంశం నుండి
T2 ∝ r³ or T ∝ r^3/2 మరియు కాలము T గురుత్వ త్వరణము ‘g’, కక్ష్యా వ్యాసార్ధము R లపై ఆధారపడును.
T ∝ r^3/2 g^a R^b ఇందులో a, bల మితులు g మరియు R ల మితులకు సమానము అనుకోండి.
(లేదా) T = k r^3/2 g^a R^b → (1)
ఇందులో k మితులు లేని స్థిరాంకము.
(1) వ సమీకరణం నుండి
[M⁰L⁰T¹] = L^3/2(LT^-2)^a (L)^b = M⁰L^{a+b+\(\frac{3}{2}\)} T^-2a
మితుల సజాతీయతా నియమం నుండి
a + b + \(\frac{3}{2}\) = 0 → (2),
-2a = 1 ⇒ a = \(\frac{-1}{2}\)
1వ సమీకరణం నుండి \(\frac{-1}{2}\) + b + \(\frac{3}{2}\) = 0 ⇒ b = -1
‘a’ మరియు ‘b’ విలువలు సమీ. (1) లో రాయగా
T = k r^3/2 g^-1/2 R^-1
∴ ఉపగ్రహం కక్ష్యావర్తనకాలము T = \(\frac{k}{R} \sqrt{\frac{r^3}{g}}\)

ప్రశ్న 4.
క్రింది సంఖ్యల్లో సార్థక సంఖ్యలు ఎన్ని ఉన్నాయో తెలపండి.
a) 6729
b) 0.024
c) 0.08240
d) 6.032
e) 4.57 × 10⁸
సాధన:
a) 6729 ఇందులో అన్ని సంఖ్యలు సార్థక సంఖ్యలే. కావున సార్థక సంఖ్యలు ^{నాలుగు}.
b) 0.024 ఇందులో దశాంశ స్థానానికి మొదటి సున్న కాని అంకెకు మధ్య గల సున్నలు సార్థక సంఖ్యలు కావు.
∴ సార్థక సంఖ్యలు ^{రెండు}.
c) 0.08240 ఇందులో సార్థక సంఖ్యల సంఖ్య ^{నాలుగు}. (చివరల గల సున్న సార్థక సంఖ్య కావున)
d) 6.032 రెండు సున్న కాని అంకెల మధ్య గల సున్న సార్థక సంఖ్య కావున సార్థక సంఖ్యలు ^{నాలుగు}.
e) 4.57 × 10⁸ ఫలితాన్ని 10 ఘాత రూపంలో రాసేటపుడు ఫలితాన్ని కనీస సార్థక సంఖ్యల వరకే తెలపాలి. కావున సార్థక సంఖ్యలు ^మూడు.

ప్రశ్న 5.
రెండు కర్రల పొడవులు వరుసగా 12.132 సెం.మీ., 12.4 సెం.మీ. ఈ కర్రలను ఒకదాని చివర మరొకదాని చివరకు తాకునట్లు అమర్చితే మొత్తం పొడవు ఎంత ? రెండింటిని ఒకదాని పక్క మరొకటి అమర్చితే పొడవుల్లో వ్యత్యాసం ఎంత?
సాధన:
పొడవు l₁ = 12.132 సెం.మీ., l₂ = 12.4 సెం.మీ. ఈ రెంటిలో దశాంశము తరువాత కనీస సార్థక సంఖ్య ^ఒకటి.

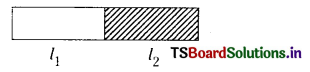
a) రెండు కర్రలను పక్కపక్కన పెడితే మొత్తం పొడవు 1 = l₁ + l₂
∴ l₁ + l₂ = 12.132 + 12.4 = 24.532 సెం.మీ.
సంకలనములో ఫలితాన్ని దశాంశ స్థానము పిమ్మట కనీస సార్థక సంఖ్యలకు సవరించాలి. కావున 24.532 ను సవరించగా 24.5 సెం.మీ.

b) కర్రల పొడవులో భేడము l = l₁ – l₂ ⇒ l = 12.4 – 12.132 = 0.268 సెం.మీ.
వ్యవకలనములో తుది జవాబును కనీస సార్థక సంఖ్యలకు సవరించగా 0.268 ని దశాంశ స్థానము పిమ్మట ఒక సార్థక సంఖ్యకు సవరించగా l₁ – l₂ = 0.3 సెం.మీ. అవుతుంది.

ప్రశ్న 6.
సమ ఘనం భుజం పొడవు 7.203 మీ. (i) ఘనం ఉపరితల వైశాల్యం, (ii) ఘనం ఘనపరిమాణాలను తగిన సార్థక సంఖ్యలకు లెక్కించండి.
సాధన:
ఘనము యొక్క ఒక భుజము a = 7.203 మీ. ఇందులో సార్థక సంఖ్యలు నాలుగు.

1. ఘనము ఉపరితల వైశాల్యము = 6a² = 6 × 7.203 × 7.203 = 311.299
   దీనిని నాలుగు సార్థక సంఖ్యలకు సవరించగా 311.3 m²
2. ఘన పరిమాణము V = a³ = (7.203)³ = 373.714
   దీనిని నాలుగు సార్థక సంఖ్యలకు సవరించగా V = 373.7 m³.

ప్రశ్న 7.
ఒక వస్తువు ద్రవ్యరాశి 2.42 g, ఘనపరిమాణం 4.7 cm³. వాటిలోని దోషాలు వరుసగా 0.01 g, 0.1 cm³ అయితే వస్తువు సాంద్రతలో గరిష్ట దోషాన్ని కనుక్కోండి.
సాధన:
ద్రవ్యరాశి m = 2.42 g;
ఘనపరిమాణము, V = 4.7 cm³,
దోషము, ∆m = 0.01 g.
దోషము, ∆V = 0.1 cc.
ద్రవ్యరాశి m లో దోషశాతము = \(\frac{\Delta \mathrm{m}}{\mathrm{m}}\) × 100 = \(\frac{0.01}{2.42}\) × 100 = \(\frac{1}{2.42}\)
ఘ.ప.లో దోషశాతము = \(\frac{0.1}{4.7}\) × 100 = \(\frac{10}{4.7}\) ;
సాంద్రత =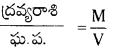
సాంద్రతలో గరిష్ఠ దోషశాతము = m లో దోషశాతము + V లో దోషశాతము
∴ సాంద్రతలో గరిష్ఠ దోషశాతము = \(\frac{1}{2.42}\) + \(\frac{10}{4.7}\) = 0.413 + 2.127 = 2.54 %

ప్రశ్న 8.
గోళం వ్యాసార్ధం కొలవడంలో దోషం 1% అయితే గోళం ఘనపరిమాణం కొలవడంలో దోషం ఎంత ?
సాధన:
వ్యాసార్ధంలో దోషశాతము 1% = \(\frac{\Delta \mathrm{r}}{\mathrm{r}}\) × 100
గోళము ఘ.ప. V ∝ r³ ⇒ ∆V = 3r²∆r ⇒ \(\frac{\Delta \mathrm{V}}{\mathrm{V}}=\frac{3 \mathrm{r}^2 \Delta \mathrm{r}}{\mathrm{r}^3}\)
ఘనపరిమాణంలో దోషశాతము \(\frac{\Delta \mathrm{V}}{\mathrm{V}}=3\left(\frac{\Delta \mathrm{r}}{\mathrm{r}}\times 100\right)\) = 3 × 1 = 3%

ప్రశ్న 9.
ద్రవ్యరాశి, వడిలో దోష శాతాలు వరుసగా 2%, 3% అయితే గతిజ శక్తిలో గరిష్ఠ దోష శాతం ఎంత ?
సాధన:
ద్రవ్యరాశిలో దోషశాతము = \(\frac{\Delta \mathrm{m}}{\mathrm{m}}\) × 100 = 2% ; వడిలో దోషశాతము = \(\frac{\Delta \mathrm{v}}{\mathrm{v}}\) × 100 = 3%
కాని గతిశక్తి K.E = \(\frac{1}{2}\) mv²
గతిశక్తిలో దోషశాతము = 1 ( ద్రవ్యరాశిలో దోషశాతము ) + 2 ( వడిలో దోషశాతము )
∴ గతిశక్తిలో దోషశాతము = 1(\(\frac{\Delta \mathrm{m}}{\mathrm{m}}\) × 100) + 2(\(\frac{\Delta \mathrm{v}}{\mathrm{v}}\) × 100) = 1 × 2 + 2 × 3 = 8%

ప్రశ్న 10.
ప్రామాణిక ఉష్ణోగ్రతా పీడనాల వద్ద ఒక మోల్ ఆదర్శవాయువు 22.4L (మోలార్ ఘనపరిమాణం) ఘనపరిమాణం ఆక్రమిస్తుంది. హైడ్రోజన్ అణు పరిమాణం సుమారుగా 1 Å, అయితే హైడ్రోజన్ మోలార్ ఘనపరిమాణానికి, పరమాణు ఘనపరిమాణానికి మధ్య నిష్పత్తి ఎంత ?
సాధన:
హైడ్రోజన్ పరమాణు పరిమాణము ≃ 1 Å = 10^-10 మీ = 10^-8 సెం.మీ.
V₁ = పరమాణు ఘనపరిమాణము = అణువుల సంఖ్య × పరమాణు ఘ.ప.
ఒక మోల్ వాయువులో అణువుల సంఖ్య = అవగాడ్రో సంఖ్య, n = 6.022 × 10²³
V₁ = \(\frac{4}{3}\)πr³ × n = \(\frac{4}{3}\) × \(\frac{22}{7}\) × [10^-8]³ × 6.022 × 10²³ = 25.23 × 10^-1 (లేదా) 2.523 సెం.మీ ³
V₂ = ఒక మోల్ వాయువు ఘ.ప. = 22.4 లీ = 2.24 × 10⁴ సెం.మీ³
∵ 1 లీ = 1000 సెం.మీ³
∴ వాయు మోలార్ ఘ.ప.కు, అణువుల ఘ.ప.కు గల నిష్పత్తి = V₂ : V₁
= 2.24 × 10⁴ : 2.523 = 10⁴.

ముఖ్యమైన అదనపు లెక్కలు

ప్రశ్న 1.
ఖాళీలను పూరించండి.
a) 1 cm భుజం పొడవు ఉండే సమఘనం ఘనపరిమాణం …………………. m³
b) 2.0cm : వ్యాసార్ధం, 10.0 cm ఎత్తు ఉండే ఘన స్థూపం ఉపరితల వైశాల్యం …………… (mm)²
c) 18 km h^-1వడితో చలిస్తున్న వాహనం 1 s లో ప్రయాణించే దూరం …………. m
d) సీసం సాపేక్ష సాంద్రత 11.3 అయితే దాని సాంద్రత …………. g cm^-3 లేదా ………… kg m^-3.
సాధన:
a) భుజము పొడవు L = 1 సెం.మీ. = 10^-2 సెం.మీ.
ఘనము ఘనపరిమాణము = L³ = (10^-2 మీ)³ = 10^-6 మీ³

b) ఇందులో, r = 2.0 సెం.మీ. = 20 మి.మీ., h = 10.0 సెం.మీ. = 100 మి.మీ.
స్థూపము ఉపరితల వైశాల్యము = (2πr) h = 2 × \(\frac{22}{7}\) × 20 × 100 మి.మీ.² = 1.26 × 10⁴ మి.మీ.²

c) వడి v = 18 km h^-1 = 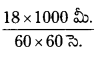= 5 మీ/సె ^-1
∴ 1 సెకనులో ప్రయాణించిన దూరము = 5 మీ.

d) సాపేక్ష సాంద్రత = 11.3
∴ సాంద్రత = 11.3 g/cc = \(\frac{11.3 \times 10^{-3} \mathrm{~kg}}{\left(10^{-2} \mathrm{~m}\right)^3}\) = 11.2 × 10³ kgm^-3

ప్రశ్న 2.
ప్రమాణాలను తగురీతిలో పరివర్తన చేయడం ద్వారా ఖాళీలను పూరించండి.
a) 1 kg m² s^-2 = ………… g cm² s^-2
b) 1 m = ………… ly (కాంతి సంవత్సరాలు)
c) 3.0 m s^-2 = ………… km h^-2
d) G = 6.67 × 10^-11 N m² (kg)^-2 = ……….. (cm)³ s^-2 g^-1.
సాధన:
a) 1 kg m² s^-2 = 1 × 10³ g (10² cm) ² s^-2 = 10⁷ g cm² s^-2

b) ఒక కాంతి సంవత్సరము = 9.46 × 10¹⁵ m
∴ 1m = \(\frac{1}{9.46 \times 10^{15}}\) కాంతి సంవత్సరం
= 1.053 × 10^-16 కాంతి సంవత్సరము

c) 3ms^-2 = 3 × 10^-3km(\(\frac{1}{60 \times 60}\)h)^-2 = = 3 × 10^-3 × 3600 × 3600 km h^-2 = 3.888 × 10⁴ km h^-2

d) G = 6.67 × 10^-11 Nm² kg^-2= 6.67 × 10^-11 (kg ms^-2)m² kg^-2
= 6.67 × 10^-11m³s^-2kg^-1
= 6.67 × 10^-11(100 cm)³ s^-2 (1000g)^-1
= 6.67 × 10^-8cm^-2s^-2g^-1

ప్రశ్న 3.
క్రింది ప్రవచనాన్ని స్పష్టంగా వివరించండి :
“పోలికకు అవసరమయ్యే ప్రామాణికాన్ని నిర్దేశించకుండా మితీయరాశిని పెద్దది లేదా చిన్నది అని పిలవడం అర్థరహితం.” దీన్ని దృష్టిలో ఉంచుకొని కింది ప్రవచనాలను అవసరమైన చోట సరిచేసి తిరిగి రాయండి.
a) పరమాణువులు అతిచిన్న వస్తువులు.
b) జెట్ విమానం ఎక్కువ వడితో చలిస్తుంది.
c) బృహస్పతి ద్రవ్యరాశి చాలా ఎక్కువ.
d) ఈ గదిలోని గాలి అధిక సంఖ్యలో అణువులను కలిగి ఉంది.
e) ఎలక్ట్రాన్ కంటే ప్రోటాన్ ద్రవ్యరాశి చాలా ఎక్కువ.
f) కాంతి వేగం కంటే ధ్వని వేగం చాలా తక్కువ.
సాధన:
ప్రవచనము సరియైనది. ఎందుకనగా పోలికకు అవసరమైన ప్రమాణం లేకుండా ఒక భౌతిక రాశి పరిమాణం పెద్దది లేదా చిన్నది అని నిర్ణయించలేము.
a) సూది మొనతో పోలిస్తే పరమాణువులు అతిచిన్న వస్తువులు అన్న ప్రవచనము సరియైనది.
b) రైలుకన్న జెట్ విమానం ఎక్కువ వడితో చలిస్తుంది అన్న ప్రవచనము సరియైనది.
c) భూమి కన్నా బృహస్పతి ద్రవ్యరాశి ఎక్కువ అన్న ప్రవచనము సరియైనది.
d) ఒక మోల్ వాయువులో గల అణువు కన్నా గదిలో గల వాయు అణువుల సంఖ్య ఎక్కువ అన్న ప్రవచనము సరియైనది.
e) ఇచ్చిన ప్రవచనము సరియైనది.
f) ఇచ్చిన ప్రవచనము సరియైనది.

ప్రశ్న 4.
పొడవును కొలవడానికి కింది వాటిలో ఏది చాలా ఖచ్చితమైన పరికరం ?
a) కదిలే స్కేలుపై 20 వెర్నియర్ విభాగాలు 19 ప్రధాన స్కేలు విభాగాలకు సమానంగా ఉండే కాలిపర్స్.
b) 1 mm పిచ్, 100 తలస్కేలు విభాగాలు ఉండే స్క్రూగేజి.
c) కాంతి తరంగదైర్ఘ్య విలువకు తక్కువ/సమానం వరకు పొడవును కొలిచే దృక్ సాధనం.
సాధన:
అతి తక్కువ కనీస కొలత గల పరికరం ఖచ్చితమైనది.
a) వెర్నియర్ కాలిపర్స్ సున్నితత్వము = 1 MSD – 1 VSD
కనీసపు కొలత = 1 MSD – \(\frac{19}{20}\) = \(\frac{1}{20}\) = 0.05 mm
(గమనిక : 1 MSD = 1 m.m అని భావించడమైనది.)

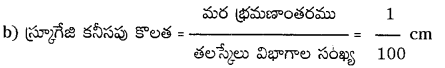
∴ కనీసపు కొలత = 0.01 మి.మీ.

c) కాంతి తరంగదైర్ఘ్యము 10^-5 cmలలో ఉంటుంది.
దీనిని కొలవడానికి కనీసం 10^-5 cm కనీస కొలత గల పరికరం కావాలి.
పైన చెప్పిన పరికరాలలో కాంతి తరంగ దైర్ఘ్యం కొలవ గల పరికరం అన్నిటికన్నా సున్నితమైనది.

ప్రశ్న 5.
క్రింది వాటికి సమాధానం వ్రాయండి.
a) నీకు ఒక దారం, మీటరు స్కేలును ఇస్తే దారం వ్యాసాన్ని ఏ విధంగా అంచనా వేస్తావు ?
b) ఒక స్క్రూగేజి పిచ్ 1.0 mm వృత్తాకార స్కేలుపై విభాగాలు 200. వృత్తాకార స్కేలుపై విభాగాల సంఖ్యను అనియతంగా పెంచడం ద్వారా స్క్రూగేజి యథార్థతను పెంచడం సాధ్యమని నీవు అనుకొంటున్నావా ?
c) వెర్నియర్ కాలిపర్స్ సహాయంతో పలుచని ఇత్తడి కడ్డీ సగటు వ్యాసాన్ని నిర్ణయించవలసి ఉంది. 5 కొలతల సమితి కంటే 100 కొలతల సమితితో వచ్చే అంచనా విలువ ఎక్కువ నమ్మదగినదని మనమెందుకు ఆశిస్తాం ?
సాధన:
a) దారము వ్యాసము చాలా తక్కువ కావున మామూలు స్కేలుతో కొలవలేము. ఇచ్చిన దారాన్ని స్కేలుపై ఒకదాని పక్కన ఒకటి ఆనుకొని ఉండే విధంగా ‘n’ చుట్లు చుట్టి ఆ చుట్ట పొడవు ‘l’ కొలవండి.
దారము వ్యాసము d = \(\frac{1}{n}\) అవుతుంది.
b) స్క్రూగేజి కనీసపు కొలత L.C. =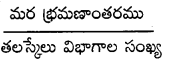
తలస్కేలు విభాగాలు పెంచితే కనీసపు కొలత తగ్గి సున్నితత్వం పెరుగుతుంది. కాని తలపరిమాణం దృష్ట్యా దానిపై ఒక పరిమితికి మించి విభాగాల సంఖ్య పెంచితే రీడింగులు ఖచ్చితంగా కొలవడం సాధ్యపడదు.

c) పరిశీలనల సంఖ్య పెంచితే కొలతలలో దోషానికి సంభావ్యత తక్కువ. ఫలితంగా 100 రీడింగుల (సగటు) అంకమధ్యమపు విలువ, 5 రీడింగుల అంకమధ్యమపు విలువ కన్నా ఖచ్చితమైనది. అందువలన రీడింగుల సంఖ్య పెరిగినకొలది సగటు విలువ ఎక్కువగా విశ్వసింపదగినదిగా ఉంటుంది.

ప్రశ్న 6.
35 mm స్లైడుపై ఒక ఇంటి ఛాయాచిత్రం వైశాల్యం 1.75 cm². ఆ స్లైడును తెరపై ప్రాజెక్ట్ చేసినపుడు ఇంటి వైశాల్యం 1.55 m² గా ఉంది. ప్రొజెక్టర్-తెర అమరిక రేఖీయ ఆవర్ధనం ఎంత ?
సాధన:
ప్రతిబింబ వైశాల్యము = 1.55 మీ² = 1.55 × 10⁴ సెం.మీ.²
ఛాయా చిత్ర వైశాల్యము = 1.75 సెం.మీ²

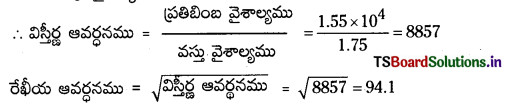
ప్రశ్న 7.
క్రింద ఇచ్చిన వాటిలో సార్థక సంఖ్యలు ఎన్ని ఉన్నాయి ?
a) 0.007 m²
b) 2.64 × 10²⁴ kg
c) 0.2370 g cm^-3‍
d) 6.320 J
e) 6.032 Nm^-2
f) 0.0006032 m²
సాధన:
a) 0.007 m² లో సార్థక సంఖ్య ఒకటి.
b) 2.64 × 10²⁴ kg లో సార్థక సంఖ్యలు మూడు.
c) 0.2370 g cm^-3 లో సార్థక సంఖ్యలు నాలుగు.
d) 6.320 J లో సార్థక సంఖ్యలు నాలుగు.
e) 6.032 Nm² లో సార్థక సంఖ్యలు నాలుగు.
f) 0.0006032 m³ లో సార్థక సంఖ్యలు నాలుగు.

ప్రశ్న 8.
దీర్ఘచతురస్రాకార లోహ పలక పొడవు, వెడల్పు, మందాలు వరుసగా 4.234 m, 1.005 m, 2.01 cm లు సరైన సార్థక సంఖ్యల వరకు ఆ పలక వైశాల్యం, ఘనపరిమాణాలను రాయండి.
సాధన:
పొడవు, 1 = 4.234 m
వెడల్పు, b = 1.005 m
మందము, t = 2.01 cm = 2.01 × 10^-2 m
పలక వైశాల్యము = 2 (l × b + b × t + t × l) = 2(4.234 × 1.005 + 1.005 × 0.0201 + 0.0201 × 4.234)
= 2(4.3604739) = 8.7209478 m²
పై కొలతలలో కనీస సార్థక సంఖ్యలు మూడు కావున తుది జవాబులో మూడు సార్థక సంఖ్యలు మాత్రమే ఉండాలి.
వైశాల్యము = 8.72 m².
ఘనపరిమాణము = l × b × t
V = 4.234 × 1.005 × 0.0201 = 0.0855289 = 0.0855 m³ (మూడు సార్థక సంఖ్యలకు సవరించగా)

ప్రశ్న 9.
ఒక పెట్టెను కిరాణా షాపుదారు వాడే త్రాసుతో తూస్తే వచ్చిన ద్రవ్యరాశి 2.300 kg. ఇప్పుడు ఈ పెట్టెకు 20.15g, 20.17g ద్రవ్యరాశులు గల రెండు బంగారు ముక్కలను కలిపారు. (a) పెట్టె మొత్తం ద్రవ్యరాశి, (b) ముక్కల ద్రవ్యరాశుల్లో వ్యత్యాసాన్ని సరైన సార్థక సంఖ్యల వరకు రాయండి.
సాధన:
పెట్టె ద్రవ్యరాశి_m = 2.3 kg
1వ బంగారు ముక్క ద్రవ్యరాశి m₁ = 20.15 g = 0.02015 kg
2వ బంగారు మొత్తం ద్రవ్యరాశి m₂ = 20.17 g = 0.02017 kg
a) మొత్తం ద్రవ్యరాశి = m + m₁ + m₂ = 2.3 + 0.02015 + 0.02017 = 2.34032 kg.
మొత్తం ద్రవ్యరాశి = 2.3 kg

b) ముక్కల ద్రవ్యరాశులలో భేదము = m₂ – m₁ = 20.17 – 20.15 = 0.02 g.

ప్రశ్న 10.
P అనే భౌతికరాశి a, b, c, d అనే నాలుగు పరిశీలించగలిగే రాశులతో కింది విధమైన సంబంధాన్ని కలిగి ఉంది:
P = a₃b₂/(\(\sqrt{c}\)d)
a, b, c, d ల కొలతల్లోని దోషశాతాలు వరుసగా 1%, 3%, 4%, 2% అయితే P లోని దోషశాతం ఎంత ? పై సంబంధం ఉపయోగించి లెక్కించిన P విలువ 3.763 అయితే, ఫలితాన్ని నీవు ఏ విలువ వరకు సవరిస్తావు ?
సాధన:

(ఇందులో సార్థక సంఖ్యలు రెండు) తుది జవాబు 3.763 ను రెండు సార్థక సంఖ్యలకు సర్దగా 3.8 అవుతుంది.

ప్రశ్న 11.
ముద్రణా దోషాలు అనేకంగా ఉండే పుస్తకంలో ఒక నిర్దిష్ట ఆవర్తన చలనం చేస్తున్న కణం స్థానభ్రంశానికి నాలుగు భిన్న ఫార్ములాలు ఉన్నాయి. అవి :
a) y = a sin 2 πt/T
b) y = a sin vt
c) y = (a/T) sin t/a
d) y = (a\(\sqrt{2}\)) (sin 2πt / T + cos 2πt / T)
(a = కణం పొందే గరిష్ఠ స్థానభ్రంశం, v = కణం వడి, T = ఆవర్తన కాలం) మితుల దృష్ట్యా తప్పు అయిన ఫార్ములాలను కొట్టి వేయండి.
సాధన:
త్రికోణమితి ప్రమేయాలలో ఆర్గుమెంట్ (ωt) పదం కోణాన్ని సూచిస్తుంది. ఇది మితి లేని రాశి.
(i) \(\frac{2 \pi \mathrm{t}}{\mathrm{T}}=\frac{\mathrm{T}}{\mathrm{T}}\) = 1= M⁰L⁰T⁰) ……………. మితి రహితము
(ii) vt= = (LT^-1)(T) = L=[M⁰ L¹ T⁰) ………….. ఈ సమీకరణ మితి రహితము కాదు
(iii) \(\frac{\mathrm{t}}{\mathrm{a}}=\frac{\mathrm{T}}{\mathrm{L}}\) = [L^-1T^-1] ……………….. ఈ సమీకరణ మితి రహితము కాదు
(iv) \(\frac{2 \pi \mathrm{t}}{\mathrm{T}}=\frac{\mathrm{T}}{\mathrm{T}}\) = 1 = [M⁰ L⁰ T⁰] ……………. మితి రహితము
∴ కావున ఇచ్చిన ఫార్ములాలలో (ii), (iii) సరియైనవి కావు.

ముఖ్యమైన ఉదాహరణ లెక్కలు

ప్రశ్న 1.
కోణాలు a) 1° (డిగ్రీ) b) 1′ (చాపం యొక్క నిమిషం లేదా ఆర్కిమిన్), c) 1″ (చాపం యొక్క సెకను, లేదా ఆర్క్ సెకను) రేడియన్లలో లెక్కించండి. 360 ° = 2π rad, 1° = 60′, 1′ = 60″ లను ఉపయోగించండి.
సాధన:
a) 360° = 2. rad నుంచి
1° = (π/180) rad = 1.745 × 10^-2 rad
b) 1° = 60′ = 1,745 × 10^-2 rad
1′ = 2.908 × 10 rad; 2.91 × 10^-4 rad
c) 1′ = 60″ = 2.908 × 10^-4 rad
1″ = 4.847 × 10^-6 rad; 4.85 × 10^-6 rad

ప్రశ్న 2.
భూమి వ్యాసంపై ఉండే రెండు వ్యతిరేక బిందువులు A, B ల నుంచి, చంద్రుడిని పరిశీలించారు. చంద్రుడి వద్ద రెండు పరిశీలనా దిశలు ఏర్పరిచే కోణం θ విలువ 1° 54′. భూమి వ్యాసం సుమారుగా 1.276 × 10⁷ m అయితే, భూమి నుంచి చంద్రుని దూరాన్ని లెక్కించండి.
సాధన:
దత్తాంశం నుంచి
θ = 1°54′ = 114′ = (114 × 60)” × (4.85 × 10^-6) rad
1″ = 4.85 × 10^-6 rad కాబట్టి,
θ = 3.32 × 10^-2 rad,
అంతేగాక, b = AB = 1.276 × 10⁷m
కాబట్టి, D = \(\frac{b}{\theta}\) సమీకరణం నుంచి భూమి-చంద్రుల మధ్య దూరం
= \(\frac{1.276 \times 10^7}{3.32 \times 10^{-2}}\) = 3.84 × 10⁸ m.

ప్రశ్న 3.
సూర్యుడి కోణీయ వ్యాసం 1920″ అని కొలిచారు. భూమి నుంచి సూర్యుడి దూరం D విలువ 1.496 × 10¹¹ m. అయితే సూర్యుడి వ్యాసం ఎంత ?
సాధన:
సూర్యుడి కోణీయ వ్యాసం, α = 1920″ = 1920 × 4.85 × 10^-6 rad = 9.31 × 10^-3 rad
సూర్యుడి వ్యాసం,
d = αaD
= (9.31 × 10^-3) × (1.496 × 10¹¹) m
= 1.39 x 10⁹m.

ప్రశ్న 4.
థర్మామీటరుతో రెండు వస్తువుల ఉష్ణోగ్రతలను t₁ = 20 °C ± 0.5 °C, t₂ = 50 °C ± 0.5 °C గా కొలిచారు. వాటి ఉష్ణోగ్రతా భేదాన్ని, దానిలోని దోషాన్ని లెక్కించండి.
సాధన:
t’ = t₂ – t₁ = (50 °C ± 0.5 °C) – (20 °C ± 0.5 °C) t’ = 30 °C ± 1 °C

ప్రశ్న 5.
నిరోధం R = V/I, ఇందులో V = (100 ± 5)V, I = (10 ± 0.2)A. అయితే R లోని దోష శాతాన్ని కనుక్కోండి.
సాధన:
V లోని దోష శాతం 5, అలాగే I లో దోష శాతం 2. కాబట్టి R లో మొత్తం దోషం 5 + 2 = 7%.

ప్రశ్న 6.
లఘులోలకం డోలనావర్తన కాలం T = 2π \(\sqrt{L / g}\).1 mm తెలిసిన యథార్థతతో కొలచిన L విలువ 20.0 cm. 100 డోలనాలకు పట్టిన కాలాన్ని 18 పృథక్కరణం ఉన్న చేతి గడియారంతో 90s అని కనుక్కొన్నారు. అయితే g విలువను నిర్ణయించడంలో యథార్థత ఎంత ?
సాధన:
g = 4π²L/T²
ఇక్కడ T = \(\frac{t}{n}\), ΔΤ = \(\frac{\Delta t}{n}\) కాబట్టి \(\frac{\Delta \mathrm{T}}{\mathrm{T}}=\frac{\Delta \mathrm{t}}{\mathrm{t}}\). ఈ L, t రెండింటిలోని దోషాలు కనీసపు కొలత దోషాలు. కాబట్టి
(Δg/g) = (ΔL/L) + 2(ΔT/T)
= \(\frac{0.1}{20.0}+2\left(\frac{1}{90}\right)\) = 0.027
అందువల్ల g లోని దోషశాతం
100 (Δg/g) = 100(ΔL/L) + 2 × 100 (ΔT/T)
= 3%.

ప్రశ్న 7.
ఒక ఘనం యొక్క ఒక్కొక్క భుజం పొడవును 7.203 mగా కొలిచారు. దాని మొత్తం ఉపరితల వైశాల్యం, ఘనపరిమాణాల విలువలను తగిన సార్థక సంఖ్యల వరకు, కనుక్కోండి.
సాధన:
కొలచిన పొడవులో నాలుగు సార్థక సంఖ్యలు ఉండటం వల్ల మనం లెక్కించే వైశాల్యం, ఘనపరిమాణాలను కూడా నాలుగు సార్థక సంఖ్యల వరకే సవరించవలసి ఉంటుంది.
ఘనం ఉపరితల వైశాల్యం = 6(7.203)²m²
= 311.299254 m²
= 311.3 m²
ఘనం ఘనపరిమాణం = (7.203)³ m³
= 373.714754 m³
= 373.7 m³

ప్రశ్న 8.
5.74 g పదార్థం 1.2 cm³ ఘనపరిమాణం ఆక్రమిస్తుంది. సార్థక సంఖ్యలను దృష్టిలో ఉంచుకొని దాని సాంద్రత విలువను వ్యక్తపరచండి.
సాధన:
కొలచిన ద్రవ్యరాశిలో మూడు సార్థక సంఖ్యలు ఉంటే కొలచిన ఘనపరిమాణంలో రెండే సార్ధక సంఖ్యలు ఉన్నాయి కాబట్టి, సాంద్రత విలువను 2 సార్థక సంఖ్యల వరకు మాత్రమే వ్యక్తపరచాలి.
సాంద్రత = \(\frac{5.74}{1.2}\) g cm^-3
= 4.8 g cm^-3.