TS Inter 1st Year Physics Notes Chapter 3 సరళరేఖాత్మక గమనం

Here students can locate TS Inter 1st Year Physics Notes 3rd Lesson సరళరేఖాత్మక గమనం to prepare for their exam.

TS Inter 1st Year Physics Notes 3rd Lesson సరళరేఖాత్మక గమనం

→ గమనము : పరిసరాలతో పోల్చినపుడు కాలానుగుణంగా వస్తువు స్థానంలో కలిగే మార్పును గమనము

→ శుద్ధగతి శాస్త్రము : గమనానికి కారణాలు ప్రస్తావించకుండా గమనాన్ని వర్ణించే పద్ధతులను వివరించే శాస్త్రము.

→ సరళరేఖాత్మక గమనము : వస్తువు యొక్క గమనము ఒక సరళరేఖకు మాత్రమే పరిమితమైతే ఆ గమనాన్ని సరళరేఖాత్మక గమనము అంటారు.

→ స్థానభ్రంశము (S) : వస్తువు స్థానంలో మార్పును స్థానభ్రంశము అంటారు. ఇది సదిశరాశి. అనగా దిశ, పరిమాణములను కలిగి ఉంటుంది.

→ పథం పొడవు (Path Length) : వస్తువు ప్రయాణమార్గం మొత్తం పొడవును పథం పొడవు అంటారు. గమనిక : వస్తువు స్థానభ్రంశపు పరిమాణం, దాని పథం పొడవు సమానం కావచ్చు, కాకపోవచ్చు. ఒక గమన మార్గానికి స్థానభ్రంశం సున్న అయినప్పటికి పథం పొడవు సున్న కాదు.

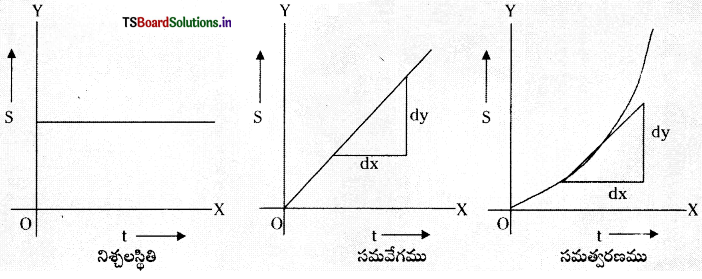
→ స్థానభ్రంశకాల వక్రాలు : వస్తువు స్థానభ్రంశము ‘S’ ను Y – అక్షం మీద, కాలము (t) ని X – అక్షం మీద తీసుకొని గీసిన రేఖాపటాన్ని స్థానభ్రంశకాల వక్రము అంటారు.
(a) నిశ్చల స్థితిలో ఉన్న వస్తువు స్థానభ్రంశకాల వక్రం X – అక్షానికి సమాంతరంగా గల సరళరేఖ.
(b) సమవేగంతో చలించే వస్తువుకు స్థానభ్రంశకాలవక్రము X- అక్షంతో కొంత కోణం చేయు సరళరేఖ. ఈ సరళరేఖ వాలు \(\left(\frac{d y}{d x}\right)\) వస్తువు సమవేగాన్ని ఇస్తుంది.
(c) సమత్వరణంతో చలించే వస్తువు స్థానభ్రంశకాల వక్రము ఒక వక్రరేఖ. దీని వాలు పైకి పోయిన కొద్ది పెరుగుతుంది. ఈ వక్రం యొక్క వాలు \(\left(\frac{d y}{d x}\right)\) ఆ క్షణం వద్ద వస్తువుకు గల వేగాన్ని తెలుపుతుంది.

→ సగటు వేగము : వస్తువు యొక్క మొత్తం స్థానభ్రంశము మరియు ప్రయాణించిన మొత్తం కాలముల నిష్పత్తిని సగటు వేగము అంటారు. ప్రమాణము మీ/సెకను. ఇది సదిశరాశి.
సగటు వేగము V̅ = \(\frac{X_2-X_1}{t_2-t_1}=\frac{\Delta X}{\Delta t}\)

→ సగటు వడి : నియమితకాలంలో వస్తువు ప్రయాణించిన పథం పొడవు మరియు కాలముల నిష్పత్తిని సగటు వడి అంటారు. ఇది అదిశరాశి. ప్రమాణము మీ/సె.

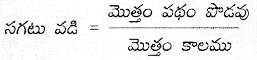
గమనిక : వడికి దిశ లేకపోవడం. వల్ల ఇది ఎల్లపుడూ ధనాత్మకము. కాని వేగం దిశను బట్టి ధనాత్మకము లేదా ఋణాత్మకంగా ఉండవచ్చు.

→ తత్కాల వేగము : కాలవ్యవధి Δt అత్యల్పమైనప్పుడు కాలవ్యవధి మరియు వస్తువు స్థానభ్రంశాల నిష్పత్తిని తత్కాల వేగము లేదా తాక్షణిక వేగము అంటారు.
తాక్షణిక వేగము \(\overline{\mathrm{V}}={Lt}_{\Delta t \rightarrow 0} \frac{\Delta \mathrm{X}}{\Delta \mathrm{t}}=\frac{\mathrm{dX}}{\mathrm{dt}}\)
గమనిక : తత్కాల వేగము సగటు వేగానికి సమానం కావచ్చు లేదా కాకపోవచ్చు.

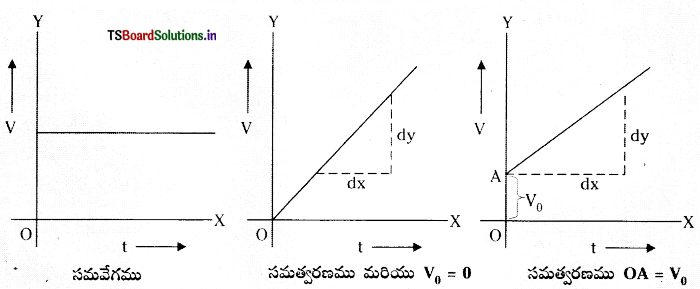
→ వేగ కాల వక్రాలు (V-t గ్రాఫ్) : వేగము Vని Y- అక్షం మీద, కాలము t ని X- అక్షం మీద తీసుకొని గీచిన రేఖా పటాన్ని వేగ కాల వక్రము అంటారు. వేగ కాల వక్రాలలో
(a) సమవేగంతో చలించే వస్తువు వేగ కాల వక్రం X- అక్షానికి సమాంతరంగా గల సరళరేఖ.
(b) నిశ్చలస్థితి నుండి బయలుదేరి సమత్వరణంతో చలించే వస్తువు వేగ – కాల వక్రం మూల బిందువు గుండా పోవు సరళరేఖ.
(c) తొలి వేగం ‘V₀‘ తో బయలుదేరి సమత్వరణంతో చలించు వస్తువు వేగకాలవక్రం కొంత Y అంతరఖండం కలిగి X- అక్షంతో కొంత కోణం చేయు సరళరేఖ. దీని Y అంతర ఖండం తొలి వేగం ‘V₀‘ ను ఇస్తుంది.
(d) వేగ కాల వక్రం వాలు వస్తువు సమత్వరణం ‘a’ ను ఇస్తుంది.
(e) వేగ కాల వక్రం కింద గల వైశాల్యం వస్తువు మొత్తం స్థానభ్రంశం ‘s’ ను తెలియజేస్తుంది.
(f) వేగ కాల వక్రాల నుండి గతి శాస్త్ర సమీకరణములు V = V₀ + at, X = V₀t + \(\frac{1}{2}\) at², V² – V₀² = 2ax లను ఉత్పాదించవచ్చు.

→ త్వరణము (a) : నిర్దిష్ట కాలవ్యవధిలో వేగంలోని మార్పును త్వరణం అంటారు. ఇది సదిశ. ప్రమాణము మీ/సె²
త్వరణము a̅ = \(\frac{V_2-V_1}{t_2-t_1}=\frac{\Delta V}{\Delta t}\) లేదా a̅ = \(\frac{V-V_0}{t-t_0}\)

→ తత్కాల త్వరణము (a) : కాలవ్యవధి Δt అత్యల్పమైనప్పుడు వస్తువు వేగంలో మార్పుకు, కాలమునకు గల నిష్పత్తిని తత్కాల లేదా తాక్షణిక త్వరణం అంటారు.
తాక్షణిక త్వరణము a̅ = \({Lt}_{\Delta t \rightarrow 0} \frac{\Delta \mathrm{V}}{\Delta \mathrm{t}}=\frac{\mathrm{dV}}{\mathrm{dt}}\)
గమనిక : త్వరణము సదిశరాశి కావడం వల్ల ఇది ధనాత్మకము లేదా ఋణాత్మకంగా ఉండవచ్చు. వస్తువుకు ఋణత్వరణము (-a) ఉంటే దాని వేగము క్రమంగా తగ్గుతుంది.

→ స్వేచ్ఛాపతనము : వస్తువును కొంత ఎత్తు నుండి జారవిడిస్తే అది స్వేచ్ఛాపతనంలో ఉంది అంటారు. ఇటువంటి వస్తువుకు a = g మరియు తొలివేగం V₀ = 0, స్థానభ్రంశము = Y.

→ స్వేచ్ఛాపతనంలోని వస్తువు సమీకరణాలు : (ఊర్ధ్వ దిశను ధనాత్మకంగా భావిస్తే)

• V = 0 – gt = -9,8t m/s
• Y = 0 – \(\frac{1}{2}\)gt² = -4.9121
• V² = 0 – 2gy = -19.6y m/s

గమనిక : వేగకాలవక్రాలతో వస్తువు వాస్తవ చలనాన్ని విశదీకరించడానికి వీలుగా ఊర్ధ్వ దిశలో త్వరణాన్ని ధనాత్మకంగా తీసుకుంటారు.

→ గెలీలియో బేసిసంఖ్యల నియమము: స్వేచ్ఛాపతనంలో ఉన్న వస్తువు వరుస సెకనులలో ప్రయాణించిన స్థానభ్రంశాల నిష్పత్తి 1:3:5:7 ……. గా గల బేసి సంఖ్యల గుణిజంగా ఉంటుంది.

→ వాహనాలను నిలిపే దూరము : వేగంగా చలించే వాహనానికి బ్రేకులు వేయడం వల్ల అది ఆగిపోయే దూరము వస్తువు తొలివేగము (V₀) మరియు బ్రేకుల ఋణత్వరణ సామర్థ్యం మీద ఆధారపడుతుంది.
ఆగిపోవు దూరము X = \(\frac{V_0^2}{2 a}\)

→ ప్రతిస్పందన కాలము : మనం ఏదైనా ఒక సంఘటనను చూచినపుడు పరిస్థితి అర్థం చేసుకొని ప్రతిచర్య ప్రారంభించడానికి పట్టే కాలము ప్రతిస్పందన కాలము.
ఉదా : చలిస్తున్న వాహనానికి ఒక బాలుడు అకస్మాత్తుగా అడ్డం వస్తే దానిని గ్రహించి వాహనానికి బ్రేకులు వేయడానికి తీసుకున్న సమయము.

→ సాపేక్ష వేగము : A, B అను రెండు వస్తువులు చలనంలో ఉంటే ఒక వస్తువు A దృష్ట్యా B చలనము లేదా B దృష్ట్యా వస్తువు A చలనాన్ని వివరించడాన్ని సాపేక్ష చలనం అంటారు.
ఉదా : A, B వస్తువుల వేగాలు V_A, V_B అయితే B దృష్ట్యా A యొక్క వేగము V_AB = V_A – V_B (A, B లు ఒకే దిశలో చలిస్తుంటే)
A దృష్ట్యా B వేగము V_BA = V_B – V_A (A, B లు ఒకే దిశలో చలిస్తుంటే)
ఈ సందర్భంలో V_AB = -V_BA
A, B లు వ్యతిరేక దిశలలో చలిస్తుంటే V_BA – V_AB = V_A + V_B.

→ ఏకరీతి లేదా సమవేగములో ప్రయాణిస్తున్న వస్తువుకు s = vt.

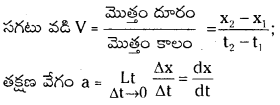
→ స్థానభ్రంశము మరియు కాలంల రేఖాపటపు వాలు వేగాన్నిస్తుంది.

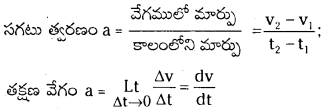
→ వేగము కాల వక్రము యొక్క వాలు త్వరణాన్ని సూచిస్తుంది.

→ వేగము – కాల వక్రము క్రింది వైశాల్యము, మొత్తం స్థానభ్రంశమునకు సమానము.

→ సమవేగముతో ప్రయాణిస్తున్న వస్తువు యొక్క v-t వక్రము, x – అక్షమునకు సమాంతరముగా ఉంటుంది.

→ సమ త్వరణంతో ప్రయాణిస్తున్న వస్తువు యొక్క v – t వక్రము X – అక్షంతో సమచాలు గల సరళరేఖను సూచిస్తుంది.

→ చలన సమీకరణాలు

• v = u + at
• s = ut + \(\frac{1}{2}\)gt²
• v² – u² = 2as

→ nవ సెకనులో వస్తువు ప్రయాణించిన దూరము S_n = u + a (n – \(\frac{1}{2}\)) లేదా u + \(\frac{a(2 n-1)}{2}\)

→ స్వేచ్ఛగా క్రిందికి పడుతున్న వస్తువు చలన సమీకరణాలు

• v = gt
• \(\frac{1}{2}\)gt²
• v² – u² = -2gh

→ నేల నుంచి నిట్టనిలువుగా పైకి ప్రక్షేపించిన వస్తువు చలన సమీకరణాలు

• v = u – gt
• h = ut – \(\frac{1}{2}\)gt²
• v² – u² = -2gh
• ఆరోహణ కాలము t_a = \(\frac{u}{g}\) అవరోహణ కాలము t_d = \(\frac{u}{g}\)
• మొత్తం ప్రయాణ కాలము T = t_a + t_d = 2t = \(\frac{2u}{g}\)

→ ఎత్తున్న శిఖరం నుండి నిలువుగా ‘u’ వేగంతో ప్రక్షేపించిన శిఖరం ఎత్తు h = – ut+ \(\frac{1}{2}\)gt² అను సమీకరణం నుండి వాడండి.
ఇందులో, t = మొత్తం ప్రయాణ కాలం.