TS Inter 1st Year Physics Notes Chapter 2 ప్రమాణాలు, కొలత

Here students can locate TS Inter 1st Year Physics Notes 2nd Lesson ప్రమాణాలు, కొలత to prepare for their exam.

TS Inter 1st Year Physics Notes 2nd Lesson ప్రమాణాలు, కొలత

→ ప్రాథమిక రాశి : ఇతర భౌతిక రాశులపై ఆధారపడక స్వేచ్ఛగా మనగలిగిన భౌతిక రాశులను ప్రాథమిక రాశులు అంటారు.
ఉదా : ద్రవ్యరాశి, పొడవు, కాలము వంటివి.

→ ఉత్పన్న రాశి : ప్రాథమిక రాశుల కలయిక వలన ఏర్పడిన భౌతిక రాశులను ఉత్పన్న రాశులు అంటారు. ఉదా : వేగము, బలము వంటివి.

→ ప్రమాణము : ఏదైనా భౌతికరాశిని కొలవడంలో అంతర్జాతీయంగా ఆమోదం పొందిన నిర్దేశిత ప్రమాణ విలువతో పోల్చడం జరుగుతుంది. దీనినే ప్రమాణము అంటారు.

→ ప్రాథమిక లేదా మూల ప్రమాణము : ప్రాథమిక భౌతిక రాశులను కొలవడానికి వాడే ప్రమాణాన్ని మూల ప్రమాణము అంటారు.
ఉదా : పొడవు → మీటరు, ద్రవ్యరాశి → కిలోగ్రాము, కాలము → సెకను వంటివి.

→ ఉత్పన్న ప్రమాణము : ఉత్పన్న రాశులను కొలవడానికి వాడే ప్రమాణాలను ఉత్పన్న ప్రమాణాలు అంటారు.
ఉదా : వైశాల్యము →చదరపు మీటరు, వేగము → మీటరు / సెకను వంటివి.

→ అంతర్జాతీయ ప్రమాణాలు (S.I. ప్రమాణము) – ప్రాథమిక రాశులు : అంతర్జాతీయ పధ్ధతి (S.I. పద్ధతి) లో ఏడు ప్రాథమిక రాశులు, రెండు సంపూరక రాశులు ఉన్నాయి. వీటిని కొలవడానికి ఏడు మూల ప్రమాణాలు, రెండు సంపూరక ప్రమాణాలు ఉన్నాయి.

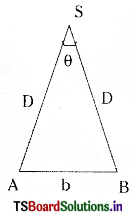
→ అధిక దూరాలను కొలవడం : అధిక దూరాలను కొలవడానికి దృష్టి విక్షేప పద్ధతి వాడతారు. ఈ పద్ధతిలో సుదూరంగా ఉన్న వస్తువును రెండు వేరు వేరు స్థానాల నుండి పరిశీలిస్తారు. ఆ స్థానముల మధ్య దూరము ‘b’, ఆ స్థానముల నుండి వస్తువును చూసిన కోణము ‘θ’ ల ఆధారంగా వస్తువు దూరాన్ని లెక్కిస్తారు. ఇందులో ‘θ’ ని పారలాక్టిక్ కోణము అంటారు.
వస్తువు దూరము D = \(\frac{b}{\theta}\)

→ అత్యల్ప దూరాలను కొలవడం : అత్యల్ప దూరాలను కొలవడానికి దృశా సూక్ష్మదర్శిని వాడతారు. ఇది కొలవ గల కనీస దూరము దృశ్యకాంతి తరంగదైర్ఘ్యం మీద ఆధారపడుతుంది. ఇది సుమారు 7000 Å నుండి 4000 Å ల మధ్య ఉంటుంది.
ఇంకా తక్కువ దూరాలను కొలవడానికి ఎలక్ట్రాన్ సూక్ష్మదర్శిని వాడతారు. ఇది కొలవగల కనీస దూరం ఎలక్ట్రాన్ తరంగదైర్ఘ్యంపై ఆధారపడుతుంది. ఈ పరికరం కొలవగల కనీస దూరం సుమారు 1Å.

→ ఓలిక్ ఆమ్ల అణుపరిమాణం అంచనా వేసే పద్ధతి : సుమారు 1 cm³ ఓలిక్ ఆమ్లాన్ని 20 cm³ ఆల్కహాల్లో కరిగించి దాని నుండి మరల 1 cm³ ద్రావణాన్ని తీసుకొని దీనిని మరల 20 cm³ ఆల్కహాల్లో కరిగిస్తారు. ఇపుడు ఈ ద్రావణంలో ఓలిక్ ఆమ్ల గాఢత \(\frac{1}{20 \times 20}\)/cm³.

ఒక నీటి తొట్టెలో కొంచెం లైకోపోడియం పొడి చల్లి దానిపై కొద్ది చుక్కలు (n) ఓలిక్ ఆమ్ల ద్రావణాన్ని వేస్తారు. ఇది దాదాపు అణుమందం గల పొరగా విస్తరిస్తుంది. ఈ పొర వ్యాసార్ధాన్ని, దాని నుండి పొర వైశాల్యాన్ని (A) లెక్కగడతారు. n చుక్కల ద్రావణం ఘనపరిమాణం లెక్కగడతారు.
ఓలిక్ ఆమ్లం పొర ఘనపరిమాణము = nv\(\frac{1}{20 \times 20}\)

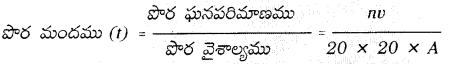
ఓలిక్ ఆమ్లం పొర అణుమందం కలిగి ఉన్నదని భావిస్తే ఈ విలువ ఓలిక్ ఆమ్లం అణువ్యాసానికి సమానము.

→ ఏకీకృత పరమాణు ద్రవ్యరాశి (united atomic mass unit) :
కార్బన్ ఐసోటోపు ఐన C-12 కర్బన పరమాణు ద్రవ్యరాశిలో \(\frac{1}{12}\) ప్రమాణంగా తీసుకున్నారు. దీని విలువ 1.66 × 10^-27 కి.గ్రా.
1 a.m.u. = \(\frac{1}{12}\)¹²₆C = 1.66 × 10^-27 కి.గ్రా.

→ పరమాణు గడియారాలు : కాలాన్ని ప్రామాణికంగా కొలవడానికి ఆధునిక పద్ధతిలో సీజియం గడియారాన్ని వాడుతున్నారు. దీనినే పరమాణు గడియారం అంటారు. దీనిలో సీజియం 133 ఐసోటోపు వాడతారు.

→ యథార్థత (Accuracy) : మనం కొలిచిన విలువ, మనం కొలవవలసిన భౌతికరాశి నిజమైన విలువకు ఎంత దగ్గరగా ఉన్నదో తెలియజేయు కొలమానాన్ని యథార్థత అంటారు.

→ ఖచ్చితత్వము (Precision) : ఖచ్చితత్వము అనేది మనం ఒక పరికరంతో ఎంత కనిష్ఠ అవధి వరకు ఇచ్చిన భౌతికరాశిని కొలవగలమో తెలియజేస్తుంది.
మనం కొలవగలిగిన కనిష్ఠ అవధి ఎంత తక్కువ ఐతే ఆ పరికరం ఖచ్చితత్వం అంత ఎక్కువ.
ఉదా :

• స్క్రూగేజి కనీసపు కొలత 0.01 మి.మీ.;
• వెర్నియర్ కాలిపర్స్ కనీసపు కొలత 0.1 మి.మీ.

ఈ రెండు పరికరాలలో స్క్రూగేజి సున్నితమైనది. కొన్ని సందర్భాలలో కొలతకు తక్కువ యథార్థత ఉన్నప్పటికి మెరుగైన ఖచ్చితత్వం ఉండవచ్చు.

→ దోషం : ఏదైనా భౌతికరాశి యొక్క కొలతలో గల అనిశ్చితత్వాన్ని దోషం అంటారు.

→ క్రమ దోషాలు (Systematic errors) : ఎల్లపుడూ ఒకే దిశలో వచ్చే దోషాలు క్రమ దోషాలు. ఇవి ఉంటే ఎల్లపుడూ ధనాత్మకంగాను లేదా ఎల్లపుడూ ఋణాత్మకంగాను ఉంటాయి.
ఉదా :

• స్క్రూగేజి యొక్క శూన్యాంశదోషము;
• తప్పుగా క్రమాంకనం చేసిన థర్మామీటరు వంటివి. తగిన సవరణలు చేయడం ద్వారా క్రమదోషాలను నివారించవచ్చు.

→ పరికరం వల్ల దోషాలు : అసమగ్ర రూపకల్పన లేదా పరికరాన్ని అసమగ్రంగా క్రమాంకనం చేయడం వల్ల పరికరంలో ఉండే శూన్యాంశ దోషము వంటివి.

→ వ్యక్తిగత దోషాలు : ఇది వ్యక్తి అనుసరించే విధానం, పరికరాలను సక్రమంగా అమర్చకపోవడం వంటి వాటిపై ఆధారపడుతుంది.
ఉదా : దృష్టి విక్షేప దోషం వంటివి.

→ యాదృచ్ఛిక దోషాలు : ఇవి క్రమరహితంగా ఏర్పడతాయి. వీటి సంజ్ఞ, పరిమాణములు కూడా యాదృచ్ఛికమైనవి. ఇవి ప్రయోగం జరుగుతున్నపుడు ఊహించని మార్పుల వలన కలుగుతాయి.
ఉదా : ఓల్టేజిలోని హెచ్చుతగ్గులు, వాతావరణంలోని మార్పులవంటివి.

→ కనీస కొలత దోషం : ఇది పరికరం కొలవగలిగే అత్యల్ప కొలతపై ఆధారపడి ఉంటుంది. ఒక పరికరంతో కొలిచిన విలువలు ఆ పరికరం కనీస కొలత వరకే ఖచ్చితంగా ఉంటాయి.

→ అంకమధ్యమము : అన్ని విలువల అంకగణిత సగటును ఖచ్చితమైన విలువగా తీసుకుంటాము. దీనిని అంకమధ్యమము అంటారు.

→ పరమదోషం : మనం కొలచిన నిజమైన విలువకు, వ్యక్తిగత కొలత యొక్క విలువకు గల తేడాను కొలతలోని పరమదోషం అంటారు.
పరమదోషం |Δa| = |a_mean – a_i| = |నిజమైన విలువ – కొలిచిన విలువ|

→ మధ్యమ పరమదోషం : పరమదోషాలు అన్నింటి యొక్క అంకమధ్యమాన్ని మధ్యమ పరమదోషం అంటారు.
Δа_సగట = \(\frac{\left|\Delta \mathrm{a}_1\right|+\left|\Delta \mathrm{a}_2\right|+\left|\Delta \mathrm{a}_3\right|+\ldots .\left|\Delta \mathrm{a}_{\mathrm{n}}\right|}{\mathrm{n}}=\frac{1}{\mathrm{n}} \sum_{\mathrm{i}=1}^{\mathrm{n}} \Delta \mathrm{a}_{\mathrm{i}}\)

→ సాపేక్ష దోషం : మధ్యమ పరమదోషానికి మరియు మధ్యమ విలువకు గల నిష్పత్తిని సాపేక్షదోషం అంటారు.

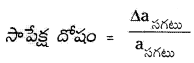
→ దోషశాతం : సాపేక్షదోషాన్ని 100చే గుణించి శాతం రూపంలో ప్రకటిస్తే దానినే దోషశాతం అంటారు.

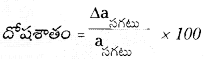
→ సంకలనం లేదా వ్యవకలనంలో దోషాల విభజన :
x = a + b గా తీసుకుంటే ‘a’ లో దోషం ‘Δa’ మరియు ‘b’ లో దోషం ‘Δb’ అయితే
సంకలనంలో దోషము Δx = Δa + Δb అనగా ‘a’ మరియు ‘b’ ల పరమదోషాల మొత్తం.

→ గుణకారం మరియు భాగహారములతో దోషాల వ్యాపనము :
x = ab లేదా x = లుగా తీసుకుంటే ‘a’ లో సాపేక్షదోషం \(\frac{\Delta a}{a}\) మరియు ‘b’ లో సాపేక్షదోషం \(\frac{\Delta b}{b}\) ‘b’ అయితే గుణకారం మరియు భాగహారంలో సాపేక్షదోషాన్ని \(\frac{\Delta \mathrm{x}}{\mathrm{x}}=\frac{\Delta \mathrm{a}}{\mathrm{a}}+\frac{\Delta \mathrm{b}}{\mathrm{b}}\) గా రాయవచ్చు. అనగా ‘a’ మరియు ‘b’ ల యొక్క సాపేక్ష దోషాల మొత్తం.

→ ఘాతాంక ప్రమేయాలతో కూడిన గుణకారాలు మరియు భాగహారాలలో దోషాల వ్యాపనము :
x = \(\frac{a^{p^p} b^q}{c^r}\) అయిన x = a^p b^q c^-r
x లోని గరిష్ఠ సాపేక్ష దోషం \(\frac{\Delta \mathrm{x}}{\mathrm{x}}=\mathrm{p}\left(\frac{\Delta \mathrm{a}}{\mathrm{a}}\right)+\mathrm{q}\left(\frac{\Delta \mathrm{b}}{\mathrm{b}}\right)+\mathrm{r}\left(\frac{\Delta \mathrm{c}}{\mathrm{c}}\right)\)

→ సార్థక సంఖ్యలు : ఏదైనా కొలతలో వాస్తవంగా కొలచిన విలువలో గల అంకెలతో పాటు ఒక అదనపు అంకెను కలిపి సార్థక సంఖ్యలు అంటారు.
ఈ అదనపు అంకె కొలతలోని అనిశ్చితత్వాన్ని తెలియజేస్తుంది.

→ సార్థక సంఖ్యలను నిర్ణయించే నియమాలు : ఏదైనా కొలతను శాస్త్రీయంగా వ్యక్తీకరించినపుడు సార్థక సంఖ్యలను నిర్ణయించడంలో ఈ క్రింది నియమాలు పాటిస్తారు.

• శూన్యేతర అంకెలన్నీ సార్థక సంఖ్యలే.
• శూన్యేతర అంకెల మధ్య దశాంశ బిందువు ఎక్కడ ఉన్నా అవి అన్నీ సార్థక సంఖ్యలే.
• ఒకటికన్న తక్కువ ఐన సంఖ్యలలో దశాంశ బిందువు కుడి వైపున గల మొదటి సున్న కాని అంకెకు, దశాంశ బిందువుకు మధ్య గల అంకెలు సార్థక సంఖ్యలు కావు.
  దశాంశ బిందువు లేని సంఖ్యలో చివరి శూన్యేతర అంకె తరువాత గల సున్నాలు సార్థక సంఖ్యలు కావు. దశాంశ బిందువు కలిగి ఉన్న సంఖ్యలలో చివరగల సున్నాలు సార్థక సంఖ్యలు.

→ సార్థక సంఖ్యలతో జరిపే అంకగణిత పరిక్రియలో పాటించే నియమాలు :

• గుణకారం లేదా భాగహారాలలో పాల్గొనే సంఖ్యలలో గల కనిష్ఠ సార్థక సంఖ్యల వరకు తుది ఫలితం సవరించాలి.
• కూడిక లేక తీసివేతలలో కనిష్ట దశాంశ స్థానాలలో ఉండే వాస్తవ సంఖ్యల వరకు చివరి ఫలితాన్ని సవరించాలి.

→ అనిశ్చిత అంకెలను సవరించడం : సార్థక సంఖ్యలలో చివరి సార్థక సంఖ్య తరువాత గల అంకెలను చివరి సార్థక సంఖ్య వరకు సర్దుబాటు చేయడంలో ఈ క్రింది నియమాలు పాటిస్తారు.

• సర్దుబాటు చేయవలసిన అంకె 5 కన్న చిన్నదైతే దానిని వదలివేస్తారు.
• సర్దుబాటు చేయవలసిన అంకె 5 కన్న పెద్దదైతే చివరి సార్థక సంఖ్య విలువ ఒకటి పెంచుతారు.
• సర్దుబాటు చేయవలసిన అంకె 5 ఐతే
  (ఎ) చివరి సార్థక సంఖ్య సరిసంఖ్య అయితే 5ను లెక్కలోకి తీసుకోకుండా వదలివేస్తారు.
  (బి) చివరి సార్థక సంఖ్య బేసిసంఖ్య అయితే దాని విలువ ఒకటి పెంచి సరిసంఖ్యగా చేస్తారు.

→ మితి : ఒక ఉత్పన్న భౌతికరాశిని సూచించడానికి ప్రాథమిక రాశులను ఏ ఘాతము వరకు పెంచుతారో ఆ ఘాతాన్ని మితి అంటారు.
ఉదా : వేగము LT^-1 లో పొడవు మితి ‘1’. కాలము మితి ‘-1’.

→ మితి ఫార్ములా : ఏదైనా ఉత్పన్నరాశిలో గల ప్రాథమిక రాశులను వాటి ఘాతములతో సహా తెలియజేయు భౌతిక శాస్త్ర సమీకరణమును మితిఫార్ములా అంటారు.
ఉదా :

• త్వరణము – LT^-2
• బలము MLT^-2

→ మితి విశ్లేషణ ఉపయోగాలు :

• ఇచ్చిన సమీకరణాల సుసంగతిని సరిచూడటం. దీని కొరకు మితుల సజాతీయత అన్న సూత్రం వాడతారు.
• వేరు వేరు భౌతికరాశుల మధ్య సంబంధాలు రాబట్టుట.