TS Inter 1st Year Maths 1B Solutions Chapter 5 Three Dimensional Coordinates Ex 5(b)

Students must practice these TS Intermediate Maths 1B Solutions Chapter 5 Three Dimensional Coordinates Ex 5(b) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1B Three Dimensional Coordinates 5(b)

I.
Question 1.
Find the ratio in which the XZ – plane divides the line joining A (-2, 3, 4) and B(l, 2, 3). (V.S.A.Q.)
Answer:
Ratio in which XZ – plane divides the AB
= – y₁ : y₂
= – 3 : 2

Question 2.
Find the coordinates of the vertex C of ∆ABC if its centroid is the origin and the vertices A, B are (1, 1, 1) and (-2, 4, 1) respectively. (V.S.A.Q.)
Answer:
Given A (1,1,1) and B (-2, 4, 1) as two vertices of a ∆ABC and suppose C (x, y, z) is the third vertex. Given O(0, 0, 0) is the centroid.
Then 0 = \(\frac{x+1-2}{3}\) ⇒ x – 1 = 0 ⇒ x = 1
o = \(\frac{y+1+4}{3}\) ⇒ y = -5
0 = \(\frac{z+1+1}{3}\) ⇒ z = -2
∴ Coordinates of third vertex C = (1, – 5, – 2)

Question 3.
If (3, 2, -1), (4, 1, 1) and (6, 2, 5) are the three vertices and (4, 2, 2) is the centroid of a tetrahedron, find the fourth vertex. (V.S.A.Q.) (May 2011, 2005)
Answer:
Let A (3, 2, -1), B (4, 1, 1), C (6, 2, 5) and D (x, y, z) be the coordinates of vertices of a tetrahedron.
Given G = (4, 2, 2) is the centroid. Then

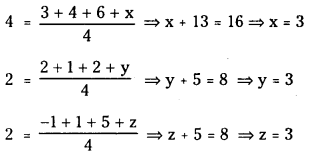
∴ Coordinates of fourth vertex D = (3, 3, 3)

Question 4.
Find the distance between the mid point of the line segment \(\overline{\mathrm{AB}}\) and the point (3, -1, 2) where A (6,3, -4) and B (-2, -1,2). (V.S.A.Q.)
Answer:
Mid point of the line AB where A (6, 3, -4) and B (-2, -1, 2) is
P = \(\left(\frac{6-2}{2}, \frac{3-1}{2}, \frac{-4+2}{2}\right)\)
= (2, 1,-1)
Suppose Q (3, -1, 2) then
PQ = \(\sqrt{(3-2)^2+(-1-1)^2+(2+1)^2}\)
= \(\sqrt{1+4+9}\) = √14 units.

II.
Question 1.
Show that the points (5, 4, 2), (6, 2, -1) and (8, -2, -7) are collinear. (V.S.A.Q.)
Answer:
Let A (5,4, 2), B (6, 2, -1) and C (8, -2, -7) be the given points.

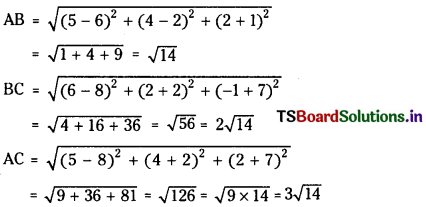
Since AB + BC = AC, the points A, B,.C are collinear.

Question 2.
Show that the points A (3, 2, -4), B( 5, 4, -6) and C (9, 8, -10) are collinear and find the ratio in which B divides \(\overline{\mathbf{A C}}\). (S.A.Q.)
Answer:
Given A (3, 2, -4), B (5, 4, -6), C (9, 8, -10) and

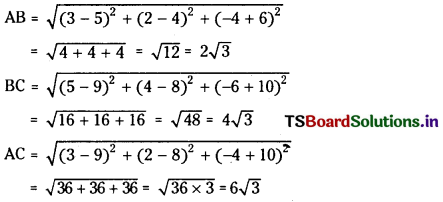
Since AB + BC = 2√3 + 4√3 = 6√3 = AC
We have the points A, B, C are collinear.
The ratio in which B divides AC is
AB : BC = 2√3 : 4√3 = 2 : 4 = 1 : 2

III.
Question 1.
If A (4, 8, 12), B (2, 4, 6), C (3, 5, 4) and D (5, 8, 5) are four points. Show that the lines \(\overleftrightarrow{\mathbf{A B}}\) and \(\overleftrightarrow{\mathbf{CD}}\) intersect. (E.Q.)
Answer:
Given A (4, 8, 12), B (2, 4, 6), C (3, 5, 4) and D (5, 8, 5) are the given points.
Coordinates of the points dividing AB in the ratio λ : 1 is
= \(\left(\frac{2 \lambda+4}{\lambda+1}, \frac{4 \lambda+8}{\lambda+1}, \frac{6 \lambda+12}{\lambda+1}\right)\) …………………….. (1)
Coordinates of the point dividing CD in the ratio μ : 1 is
= \(\left(\frac{5 \mu+3}{\mu+1}, \frac{8 \mu+5}{\mu+1}, \frac{5 \mu+4}{\mu+1}\right)\) …………………….. (2)
If the given lines intersect then these two points are same
∴ \(\frac{2 \lambda+4}{\lambda+1}=\frac{5 \mu+3}{\mu+1}\) …………………….. (3)
⇒ (2λ + 4) (μ + 1) = (5μ + 3) (λ + 1)
⇒ 2λμ + 4μ + 2λ + 4 = 5λμ + 3λ + 5μ + 3
⇒ 3λμ + λ + μ – 1 = 0
⇒ λ = – (3μ + 1) = – (μ – 1)
⇒ λ = – \(\left(\frac{\mu-1}{3 \mu+1}\right)\) ………………….. (4)
Also \(\frac{4 \lambda+8}{\lambda+1}=\frac{8 \mu+5}{\mu+1}\)
⇒ (4λ + 8) (μ + 1) = (8μ + 5) (λ + 1)
⇒ 4λμ + 8μ + 4λ + 8 = 8λμ + 5λ + 8μ + 5
⇒ 4λμ + λ – 3 = 0
⇒ (4μ + 1)λ = 3
⇒ (4μ + 1)\(\left(\frac{-(\mu-1)}{3 \mu+1}\right)\) = 3 (∵ from (4))
⇒ 4μ² – 4μ + μ – 1 = – 9μ – 3
⇒ 4μ² + 6μ + 2 = 0
⇒ 2μ² + 3μ + 1 = 0
⇒ (2μ + 1) (μ + 1) = 0
⇒ μ = – \(\frac{1}{2}\) (or) μ = – 1
μ = – 1 is not admissible
∴ μ = – \(\frac{1}{2}\)
Hence from (2)

Since the two points coincide, the given lines intersect.

Question 2.
Find the point of intersection of the lines \(\overleftrightarrow{\mathbf{A B}}\) and \(\overleftrightarrow{\mathbf{C D}}\) where
A = (7, -6, 1), B = (17, -18, -3)
C = (1, 4, -5) and D = (3, -4, 11) (E.Q.)
Answer:
Given A = (7, -6, 1), B = (17, -18, -3), C = (1, 4, -5) and D = (3, -4, 11)
Coordinates of the point dividing AB in the ratio λ : 1 are
= \(\left(\frac{17 \lambda+7}{\lambda+1}, \frac{-18 \lambda-6}{\lambda+1}, \frac{-3 \lambda+1}{\lambda+1}\right)\) …………………. (1)
Coordinates of the point dividing CD in the ratio μ : 1 are
= \(\left(\frac{3 \mu+1}{\mu+1}, \frac{-4 \mu+4}{\mu+1}, \frac{11 \mu-5}{\mu+1}\right)\) …………………. (2)
∴ \(\frac{17 \lambda+7}{\lambda+1}=\frac{3 \mu+1}{\mu+1}\)
⇒ (17λ + 4) (μ + 1) = (3μ + 1) (λ + 1)
⇒ 17λμ + 17λ + 7μ + 7 = 3λμ + 3μ + λ + 1
⇒ 14λμ + 16λ + 4μ + 6 = 0 …………………. (3)
Also \(\frac{-18 \lambda-6}{\lambda+1}=\frac{-4 \mu+4}{\mu+1}\)
⇒ – 18λμ – 6μ – 18λ – 6 = – 4λμ + 4λ – 4μ + 4
⇒ 14λμ + 22λ + 2μ + 10 = 0 ………………….. (4)
From (3) and (4)
– 6λ + 2μ – 4 = 0
⇒ 2μ = 6λ + 4 = 0
⇒ μ = 3λ + 2 ……………………… (5)
Substituting in (3) we get
⇒ 14λ (3λ + 2) + 16λ + 4(3λ + 2) + 6 = 0
⇒ 42λ² + 28λ + 16λ + 12λ + 8 + 6 = 0
⇒ 42λ² + 56λ + 14 = 0
⇒ 3λ² + 4λ + 1 = 0
⇒ (λ + 1) (3λ + 1) = 0
⇒ λ = – 1 or λ = – \(\frac{1}{3}\)
(λ = – 1 is not admissible)
∴ λ = – \(\frac{1}{3}\)

∴ These two points coincide
∴ The given lines \(\overleftrightarrow{\mathrm{AB}}\) and \(\overleftrightarrow{\mathrm{CD}}\) intersect
∴ Point of intersection = (2, 0, 3)

Question 3.
A (3, 2, 0), B(5, 3, 0, C (- 9, 6, – 3) are the vertices of a triangle. \(\overline{\mathbf{A D}}\), the bisector of ∠BAC meets \(\overline{\mathbf{B C}}\) at D. Find the coordinates of D. (E.Q.)
Answer:

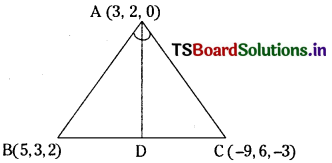
Given A = (3, 2, 0), B = (5, 3, 2), C = (-9, 6, -3) are the vertices of ∆ABC

Question 4.
Show that the points O (0, 0, 0), A (2, -3, 3), B (-2, 3, -3) are collinear. Find the ratio in which each point divides the segment joining the other two. (S.A.Q.)
Answer:
Given points are O(0, 0, 0), A (2, -3, 3) B (-2, 3, -3)

Since OA + OB = AB, the points O, A, B are collinear. Ratio in which O divides AB =
OA : OB = √22 : √22 = 1 : 1
Ratio in which A divides OB
= OA : AB = -√22 : 2√22 = – 1 : 2
Ratio in which B divides OA = AB : BO
= – 2√22 : √22 = -2 : 1
∴ A and B divide externally.