TS Inter 1st Year Maths 1A Solutions Chapter 3 Matrices Ex 3(c)

Students must practice these TS Intermediate Maths 1A Solutions Chapter 3 Matrices Ex 3(c) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1A Matrices Solutions Exercise 3(c)

Question 1.
If A = \(\left[\begin{array}{rrr}
2 & 0 & 1 \\
-1 & 1 & 5
\end{array}\right]\) and B = \(\left[\begin{array}{rrr}
-1 & 1 & 0 \\
0 & 1 & -2
\end{array}\right]\) then find (AB’)’
Answer:
We have (AB)’ = B’A’
and (AB’)’ = (B’)’ A’ = BA’ (∵ (B )’ = B)

Question 2.
If A = \(\left[\begin{array}{rr}
-2 & 1 \\
5 & 0 \\
-1 & 4
\end{array}\right]\) and B = \(\left[\begin{array}{rrr}
-2 & 3 & 1 \\
4 & 0 & 2
\end{array}\right]\) then find 2A + B’ and 3B’ – A.
Answer:

Question 3.
If A = \(\left[\begin{array}{cc}
2 & -4 \\
-5 & 3
\end{array}\right]\) then find A + A’ and A. A’ (May 2007) (Board Model Paper)
Answer:

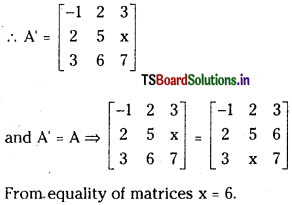
Question 4.
If A = \(\left[\begin{array}{ccc}
-1 & 2 & 3 \\
2 & 5 & 6 \\
3 & x & 7
\end{array}\right]\) is a symmetric matrix then find x.
Answer:
A matrix ‘A’ is said to be symmetric if A’ = A

Question 5.
If A = \(\left[\begin{array}{ccc}
0 & 2 & 1 \\
-2 & 0 & -2 \\
-1 & x & 0
\end{array}\right]\) is a skew symmetric matrix, find x. (May 2014, 11)
Answer:
A matrix A is said to be skew symmetric if A’ = – A
\(\left[\begin{array}{ccc}
0 & -2 & -1 \\
2 & 0 & \mathrm{x} \\
1 & -2 & 0
\end{array}\right]=\left[\begin{array}{ccc}
0 & -2 & -1 \\
2 & 0 & 2 \\
1 & -\mathrm{x} & 0
\end{array}\right]\)
from equality of matrix x = 2

Question 6.
Is \(\left[\begin{array}{ccc}
0 & 1 & 4 \\
-1 & 0 & 7 \\
-4 & -7 & 0
\end{array}\right]\) a symmetric or skew symmetric?
Answer:
Let A = \(\left[\begin{array}{ccc}
0 & 1 & 4 \\
-1 & 0 & 7 \\
-4 & -7 & 0
\end{array}\right]\) then A is symmetric if A’ = A and skew symmetric if A’ = – A
i.e., A’ = \(\left[\begin{array}{ccc}
0 & -1 & -4 \\
1 & 0 & -7 \\
4 & 7 & 0
\end{array}\right]=\left[\begin{array}{ccc}
0 & 1 & 4 \\
-1 & 0 & 7 \\
-4 & -7 & 0
\end{array}\right]\) = -A
∴ The matrix A is a skew symmetric matrix.

II.
Question 1.
If A = \(\left[\begin{array}{cc}
\cos \alpha & \sin \alpha \\
-\sin \alpha & \cos \alpha
\end{array}\right]\), show that A . A’ = A’ . A = I₂. (March 2007)
Answer:

Question 2.
If A = \(\left[\begin{array}{ccc}
1 & 5 & 3 \\
2 & 4 & 0 \\
3 & -1 & -5
\end{array}\right]\) and B = \(\left[\begin{array}{ccc}
2 & -1 & 0 \\
0 & -2 & 5 \\
1 & 2 & 0
\end{array}\right]\), then find 3A – 4B’.
Answer:

Question 3.
If A = \(\left[\begin{array}{rr}
7 & -2 \\
-1 & 2 \\
5 & 3
\end{array}\right]\) and B = \(\left[\begin{array}{rr}
-2 & -1 \\
4 & 2 \\
-1 & 0
\end{array}\right]\) then find AB’ and BA’.
Answer:

Question 4.
For any square matrix A; show that A A’ is symmetric. (March 2015-A.P)
Answer:
By definition a matrix is said to be symmetric if A’ = A.
∴(A A’)’ = (A’)’ A’ = A A’
[(∵ (AB)’ = B’A’ and (A’)’ = A]
Hence AA’ is a symmetric matrix.