TS 10th Class Maths Solutions Chapter 6 Progressions Ex 6.5

Students can practice TS Class 10 Maths Solutions Chapter 6 Progressions Ex 6.5 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 6 Progressions Exercise 6.5

Question 1.
For each geometric progression find the common ratio ‘r’, and then find a_n.

i) 3, \(\frac{3}{2}\), \(\frac{3}{4}\), \(\frac{3}{8}\),………..
Solution:

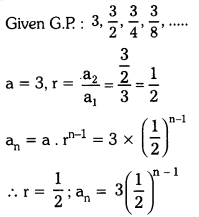
ii) 2, -6, 18, -54,…………
Solution:
Given
G.P. 2, -6, 18, -54,…………
a = 2, r = \(\frac{a_2}{a_1}\) = \(\frac{-6}{2}\) = -3
a_n = a. r^n-1 = 2 × (-3)^n-1
∴ r = -3; a_n = 2(-3)^n-1

iii) -1, -3, -9, -27,………..
Solution:
Given G.P. = – 1, – 3, – 9, – 27, ….
a = -1, r = \(\frac{a_2}{a_1}\) = \(\frac{-3}{-1}\) = 3
a_n = a . r^n-1 = (-1) × 3^n-1
∴ r = 3, a_n = (-1) × 3^n-1

iv) 5, 2, \(\frac{4}{5}\), \(\frac{8}{25}\),……….
Solution:
Given G.P: 5, 2, \(\frac{4}{5}\), \(\frac{8}{25}\),…………
a = 5, r = \(\frac{\mathrm{a}_2}{\mathrm{a}_1}\) = \(=\frac{2}{5}\)
a_n = a . r^n-1 = 5 × \(\left(\frac{2}{5}\right)^{\mathrm{n}-1}\)
∴ r = \(\frac{2}{5}\) ; a_n = 5\(\left(\frac{2}{5}\right)^{\mathrm{n}-1}\)

Question 2.
Find the 10^th and n^th term of G.P.:
5, 25, 125,……..
Solution:
Given G.P. = 5, 25, 125,……….
a = 5, r = \(\frac{a_2}{a_1}\) = \(\frac{25}{5}\) = 5
a_n = a. r^n-1 = 5 × 5^n-1 = 5^1+n-1 = 5ⁿ
∴ a₁₀ = a . r⁹ = 5 × 5⁹ = 5¹⁰
∴ a₁₀ = 5¹⁰; a_n = 5ⁿ

Question 3.
Find the indicated term of each geometric progression.

i) a₁ = 9 ; r = \(\frac{1}{3}\) ; find a₇.
Solution:
a_n = a . r^n-1
a₇ = 9 × \(\left(\frac{1}{3}\right)^{7-1}\) = 3² \(\left(\frac{1}{3}\right)^6\) = \(\frac{3^2}{3^6}\) = \(\frac{1}{3^4}\)
∴ a₇ = \(\frac{1}{3^4}\)

ii) a₁ = -12 ; r = \(\frac{1}{3}\) ; find a₆.
Solution:
a_n = a. r^n-1
a₆ = (-12) × \(\left(\frac{1}{3}\right)^{6-1}\)
= (-12) × \(\frac{1}{3^5}\) = \(\frac{-4 \times 3}{3^5}\) = \(\frac{-4}{3^4}\)
∴ a₆ = \(\frac{-4}{3^4}\)

Question 4.
Which term of the G.P.

i) 2, 8, 32,………. is 512?
Solution:
Given GP. :2, 8, 32,………. is 512
a = 2; r = \(\frac{a_2}{a_1}\) = \(\frac{8}{2}\) = 4
Let the n^th term of G.P. be 512
a_n = a . r^n-1
512 = 2 × (4)^n-1
2⁹ = 2 × (2²)^n-1
2⁹ = 2¹ × 2^2(n-1)
2⁹ = 2^2n-2+1
2⁹ = 2^2n-1
[∵ bases are equal, exponents are also equal]
∴ 2n = 9 + 1
n = \(\frac{10}{2}\) = 5
∴ 512 is the 5^th term of the given G.P

ii) \(\sqrt{3}\), 3, 3\(\sqrt{3}\),……. is 729?
Solution:

[∵ bases are equal, exponents are also equal]
\(\frac{1}{2}\)(n-1) = 6 – 1
⇒ n – 1 = 5 × 2
⇒ n = 10 + 1 = 11
∴ 729 is the 11^th term of the given G.P

iii) \(\frac{1}{3}\), \(\frac{1}{9}\), \(\frac{1}{27}\),……….. is \(\frac{1}{2187}\) ?
Solution:
Given

[∵ bases are equal, exponents are also equal]
∴ 7^th term of GP is \(\frac{1}{2187}\)

Question 5.
Find the 12^th term of a G.P whose 8^th term is 192 and the common ratio is 2.
Solution:
Given a G.P such that a₈ = 192 and
r = 2
a_n = a . r^n-1
∴ a₈ = a(2)^8-1 = 192
a.2⁷ = 192
⇒ a = \(\frac{192}{2^7}\) = \(\frac{192}{128}\) = \(\frac{12}{8}\) = \(\frac{3}{2}\)
∴ a₁₂ = a. r¹¹ = \(\frac{3}{2}\) × (2)¹¹
= 3 × 2¹⁰ = 3 × 1024 = 3072.

Question 6.
The 4^th term of a geometric progressions is \(\frac{2}{3}\) and the seventh term is \(\frac{16}{81}\). Find the geometric series.

Now substituting r = \(\frac{2}{3}\) in equation (1) we get,
a\(\left(\frac{2}{3}\right)^3\) = \(\frac{2}{3}\) ⇒ a = \(\frac{2}{3}\) × \(\frac{3}{2}\) × \(\frac{3}{2}\) × \(\frac{3}{2}\) = \(\frac{9}{4}\) ×
∴ The G.P is a, ar, ar², ar³,…………..
\(\frac{9}{4}\), \(\frac{9}{4}\) × \(\frac{2}{3}\) ; \(\frac{9}{4}\) × \(\left(\frac{2}{3}\right)^2\) …….. = \(\frac{9}{4}\), \(\frac{3}{2}\), 1,……..

Question 7.
If the geometric progressions 162, 54, 18 …. and \(\frac{2}{81}\), \(\frac{2}{27}\), \(\frac{2}{9}\),……….. have their n^th term equal, find the value of n.?
Solution:
Given G.P. :
162, 54, 18,…….. and \(\frac{2}{81}\), \(\frac{2}{27}\), \(\frac{2}{9}\),………

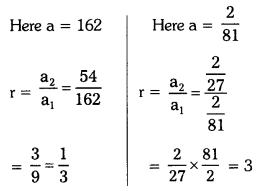
Given that n^th terms are equal
a_n = a. r^n-1
⇒ 162 × \(\left(\frac{1}{3}\right)^{\mathrm{n}-1}\) = \(\frac{2}{81}\) × (3)^n-1
⇒ 3^n-1 × 3^n-1 = 162 × \(\frac{81}{2}\)
⇒ 3^n-1+n-1 = 81 × 81
⇒ 3^2n-2 = 3⁸ [a^m . aⁿ = a^m+n]
⇒ 2n – 2 = 8
[∵ bases are equal, exponents are also equal]
2n = 8 + 2
∴ n = \(\frac{10}{2}\) = 5
The 5^th terms of the two G.Ps are equal.