TS 10th Class Maths Solutions Chapter 4 Pair of Linear Equations in Two Variables Optional Exercise

Students can practice TS 10th Class Maths Solutions Chapter 4 Pair of Linear Equations in Two Variables Optional Exercise to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 4 Pair of Linear Equations in Two Variables Optional Exercise

Question 1.
Solve the following equations :

i) \(\frac{2 x}{a}\) + \(\frac{\mathbf{y}}{\mathbf{b}}\) = 2
\(\frac{x}{a}\) – \(\frac{y}{b}\) = 4
Solution:
Given
\(\frac{2 x}{a}\) + \(\frac{\mathbf{y}}{\mathbf{b}}\) = 2 —- (1)
\(\frac{x}{a}\) – \(\frac{y}{b}\) = 4 — (2)
Adding eq.(1) & (2) \(\frac{3 x}{a}\) = 6 ⇒ x = \(\frac{6 a}{3}\) = 2a
Substituting x = 2a in the equation (1), we get
\(\frac{2}{a}\)(2a) + \(\frac{\mathrm{y}}{\mathrm{b}}\) = 2
⇒ 4 + \(\frac{\mathrm{y}}{\mathrm{b}}\) = 2
⇒ \(\frac{\mathrm{y}}{\mathrm{b}}\) = -2 ⇒ y = -2b
∴ The solution (x, y) = (7, 13)

ii) \(\frac{x+1}{2}\) + \(\frac{y-1}{3}\) = 8
\(\frac{x-1}{3}\) + \(\frac{y+1}{2}\) = 9
Solution:

Substituting y = 13 in equation (1), we get
3x + 2(13) = 47 ⇒ 3x = 47 – 26
⇒ 3x = 21 ⇒ x = \(\frac{21}{3}\) = 7
∴ The solution (x, y) = (7, 13)

iii) \(\frac{x}{7}\) + \(\frac{y}{3}\) = 5
\(\frac{x}{2}\) – \(\frac{y}{9}\) = 6
Solution:

Substituting y = 9 in equation (1) we get
3x + 7(9) = 105
⇒ 3x = 105 – 63
⇒ 3x = 42
⇒ x = \(\frac{42}{3}\) = 14
∴ The solution (x, y) = (14, 9)

iv) \(\sqrt{3}\)x – \(\sqrt{2}\)y = \(\sqrt{3}\)
\(\sqrt{5}\)x + \(\sqrt{3}\)y = \(\sqrt{3}\)
Solution:

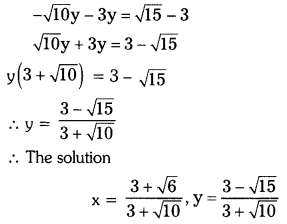
v) \(\frac{a x}{\mathbf{b}}\) – \(\frac{b y}{a}\) = a + b
ax – by = 2ab
Solution:
Given \(\frac{a x}{\mathbf{b}}\) – \(\frac{b y}{a}\) = a + b —- (1)
ax – by = 2ab —- (2)

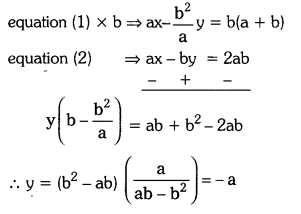
Substituting y = -a in equation (2), we get
ax – b(-a) = 2ab
⇒ ax + ab = 2ab
⇒ ax = 2ab – ab
∴ x = \(\frac{a b}{a}\) = b
∴ The solution (x, y) = (b, -a)

vi) 2^x + 3^y = 17
2^x+2 – 3^y+1 = 5
Solution:
Given, 2^x + 3^y = 17 and
2^x+2 – 3^y+1 = 5
Take 2^x = a and 3^y = b then the give equations reduce to
2^x + 3^y = 17 —- (1)
2^x.2² – 3^y. 3 = 5 ⇒ 4a – 3b = 5 —– (2)

Substituting b = 9 in equation (1), we get
a + 9 = 17 ⇒ a = 17 – 9 = 8
But a = 2^x = 8 and b = 3^y = 9
⇒ 2^x = 2³
⇒ x = 3

⇒ 3^y = 3²
⇒ y = 2
∴ The solution (x, y) is (3, 2).

Question 2.
Animals in an experiment are to be kept on a strict diet. Each animal is to receive among other things 20g of protein and 6g of fat. The laboratory technicians purchased two food mixes, A and B. Mix A has 10% protein and 6% fat. Mix B has 20% protein and 2% fat. How many grams of each mix should be used?
Solution:
Let x gms of mix A and y gms of mix B are to be mixed, then


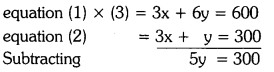
∴ y = \(\frac{300}{5}\) = 60 gm
Substituting y = 60 in equation (1), we get
x + 2 × 60 = 200 ⇒ x + 120 = 200
⇒ 200 – 120 = 80 gm
∴ Quantity of mix. A = 80 gms.
Quantity of mix. B = 60 gms.