TS 10th Class Maths Solutions Chapter 4 Pair of Linear Equations in Two Variables InText Questions

Students can practice 10th Class Maths Solutions Telangana Chapter 4 Pair of Linear Equations in Two Variables InText Questions to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 4 Pair of Linear Equations in Two Variables InText Questions

Think – Discuss

Question 1.
Two situations are given below. (Page No. 73)
i) The cost of 1 kg potatoes and 2 kg tomatoes was ₹ 30 on a certain day. After two days, the cost of 2 kg potatoes and 4 kg tomatoes was found to be ₹ 66.
ii) The coach of a cricket team of M.K. Nagar High School buys 3 bats and 6 balls for ₹ 3900. Later he buys one more bat and 2 balls for ₹ 1300.
Identify the unknowns in each situation. We observe that there are two unknowns in each case.
Solution:
i) Let the cost of 1 kg potatoes be ₹ x.
The cost of 1 kg tomatoes be ₹ y.
Given the cost of 1 kg potatoes and 2 kg tomatoes = ₹ 30
∴ x + 2y = 30
Given the cost of 2 kg potatoes and 4 kg tomatoes = ₹ 66
∴ 2x + 4y = 66
The pair of linear equations in two variables are x + 2y = 30 and 2x + 4y = 66.
We observe that there are two unknowns in this case.

ii) Let the cost of one bat be ₹ x.
The cost of one ball be ₹ y.
Given the cost of 3 bats and 6 balls = ₹ 3,900
3x + 6y = 3,900
Given 4 bats and 2 balls cost = ₹ 1,300
∴ 4x + 2y = 1,300
The pair of linear equations in two variables are 3x + 6y = 3,900 and 4x + 2y = 1300
We observe that there are two unknowns in this case.

Question 2.
Is a dependent pair of linear equations always consistent ? Why or why not ? (Page No. 79)
Answer:
If the lines intersect at a point gives the unique solution of the equations.
If the lines coincide then there are infinitely many solutions each point on the line being a solution. No, a dependent pair of linear equations are always consistent.

Try This

Mark the correct option in the following questions :

Question 1.
Which of the following equations is not a linear equation ?
a) 5 + 4x = y + 3
b) x + 2y = y – x
c) 3 – x = y² + 4
d) x + y = 0 (Page No. 75)
Solution:
a) 5 + 4x = y + 3
4x + 5 = y + 3
4x + 5 – y – 3 = 0
4x – y + 2 = 0
This equation is in the form of ax + by + c = 0 where a, b, c are real numbers.
So, the given equation is a linear equation.

b) x + 2y = y – x
x + 2y – y + x = 0
2x + y = 0
This equation is in the form of ax + by + c = 0 where a, b, c are real numbers.
So, the given equation is a linear equation.

c) 3 – x = y² + 4
3 – x – y² – 4 = 0
– x – y² – 1 = 0
x + y² + 1 = 0
This equation is not in the form of ax + by + c = 0 where a, b, c are real numbers.
∴ The given equation is not a linear equation.

d) x + y = 0
This equation is in the form of ax + by + c = 0 where a, b, c are real numbers.
So, the given equation is a linear equation.

Question 2.
Which of the following is a linear equation in one variable ? ( b )
a) 2x + 1 = y – 3
b) 2t – 1 = 2t + 5
c) 2x – 1 = x²
d) x² – x + 1 = 0 (Page No. 76)
Solution:
a) 2x + 1 = y – 3
⇒ 2x + 1 – y + 3 = 0
⇒ 2x – y + 4 = 0
Is a linear equation in two variables.
They are x and y.

b) 2t – 1 = 2t + 5
⇒ 2t – 1 – 2t – 5 = 0
⇒ -6 = 0 (False)
Is not a linear equation in one variable.

c) 2x – 1 = x² ⇒ x² – 2x + 1 = 0
Is a linear equation in one variable i.e., ‘x’.

d) x² – x + 1 = 0
Is a linear equation in one variable.
i.e., ‘x’.

Question 3.
Which of the following numbers is a solution for the equation
2(x + 3) = 18 ? ( b )
a) 5
b) 6
c) 13
d) 21 (Page No. 76)
Solution:
Given equation 2(x + 3) = 18
a) At x = 5; 2 (5 + 3) = 18
2 × 8 = 18
16 = 18 (False) Not a solution.

b) At x = 6; 2(6 + 3) = 18
2 × 9 = 18
18 = 18 (True)
x = 6 is a solution for the given equation.

c) At x = 13; 2(13 + 3) = 18
2 × 16 = 18
32 = 18 (False) Not a solution.

d) At x = 21; 2(21 + 3) = 18
2 × 24 = 18
48 = 18 (False) Not a solution.

Question 4.
The value of x which satisfies the equation 2x – (4 – x) = 5 – x is
a) 4.5
b) 3
c) 2.25
d) 0.5 ( c ) (Page No. 76)
Solution:
Given equation 2x – (4 – x) = 5 – x
a) At x = 4.5; 2 (4.5) – (4 – 4.5) = 5 – 4.5
9 – (-0.5) = (0.5)
9 + 0.5 = 0.5
9.5 = 0.5 (False)
∴ Value of x does not satisfies the equation.

b) At x = 3 ; 2(3) – (4 – 3) = 5 – 3
6 – 1 = 2
5 = 2 (False)
∴ Value of x does not satisfies the equation.

c) At x = 2.25 ; 2(2.25) – (4 – 2.25)
= 5 – 2.25
4.50-1.75 = 2.75
2.75 = 2.75 (True)
∴ Value of x satisfies the equation.

d) At x = 0.5 ; 2(0.5) – (4 – 0.5) = 5 – 0.5
1 – 3.5 = 4.5
– 2.5 = 4.5 (False)
∴ Value of x does not satisfies the equation.

Question 5.
The equation x – 4y = 5 has
a) no solution
b) unique solution
c) two solutions
d) infinitely many solutions (d) (Page No. 76)
Solution:
Only one equation with two unknowns (variables) we can find many solutions.

Question 6.
In the example above can you find the cost of each bat and ball ? (Page No. 79)
Solution:
No, we cannot find the cost of each bat and ball because the equations are geometrically shown by a pair of coincident lines. Every point on the line is a common solution to both the equations.

Question 7.
For what value of ‘p’ for the following pair of equations has a unique solution.
2x + py = -5 and 3x + 3y = -6 (Page No. 83)
Solution:
Given equations are 2x + py = -5 and 3x + 3y = -6
a₁ = 2 ; b₁ = p; c₁ = -5
a₂ = 3; b₂ = 3 ; c₂ = -6
\(\frac{\mathrm{a}_1}{\mathrm{a}_2}\) = \(\frac{2}{3}\) ; \(\frac{\mathrm{b}_1}{\mathrm{b}_2}\) = \(\frac{p}{3}\) ; \(\frac{\mathrm{c}_1}{\mathrm{c}_2}\) = \(\frac{-5}{-6}\)
Given the pair of equations has a unique solution.
∴ \(\frac{\mathrm{a}_1}{\mathrm{a}_2}\) ≠ \(\frac{\mathrm{b}_1}{\mathrm{b}_2}\) (∵ p ≠ 2)
If p = except 2 then the given pair of equations has a unique solution.

Question 8.
Find the value of ‘k’ for which the pair of equations 2x – ky + 3 = 0, 4x + 6y – 5 = 0 represent parallel lines. (Page No. 83)
Answer:
Given pair of equations
2x – ky + 3 = 0 and 4x + 6y – 5 = 0
a₁ = 2; b₁ = -k; c₁ = 3
a₂ = 4; b₂ = 6; c₂ = -5
Given the pair of lines are parallel.
∴ \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) ≠ \(\frac{c_1}{c_2}\)
\(\frac{a_1}{a_2}\) = \(\frac{\mathrm{b}_1}{\mathrm{~b}_2}\) ⇒ \(\frac{2}{4}\) = \(\frac{-\mathrm{k}}{6}\)
-4k = 2 × 6
-4k = 12
∴ k = \(\frac{12}{-4}\) = -3

Question 9.
For what value of ‘k’ for the pair of equations 3x + 4y + 2 = 0 and 9x + 12y + k = 0 represent coincident lines. (Page No. 83)
Solution:
Given pair of equations 3x + 4y + 2 = 0 and 9x + 12y + k = 0 (A.P.Mar.’16) (A.P. Jun.’15)
Given the pair of lines are coincident.
∴ \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) = \(\frac{c_1}{c_2}\)
\(\frac{a_1}{a_2}\) = \(\frac{c_1}{c_2}\) ⇒ \(\frac{3}{9}\) = \(\frac{2}{\mathrm{k}}\) ⇒ \frac{1}{3}\(\) = \(\frac{2}{k}\)
∴ k = 3 × 2 = 6

Question 10.
For what Positive values of ‘p’ the following pair of linear equations have infinitely many solutions ? (Page No. 83)
px + 3y – (p – 3) = 0
12x + py – p = 0
Solution:
Given pair of equations are px + 3y – (p – 3) = 0 and 12x + py – p = 0
a₁ = p; b₁ = 3; c₁ = -(p – 3);
a₂ = 12; b₂ = p; c₂ = -p
Given equations has infinitely many solutions.
∴ \(\frac{\mathrm{a}_1}{\mathrm{a}_2}\) = \(\frac{\mathrm{a}_1}{\mathrm{a}_2}\) = \(\frac{\mathrm{c}_1}{\mathrm{c}_2}\)
⇒ \(\frac{\mathrm{p}}{12}\) = \(\frac{3}{p}\) = \(\frac{-(p-3)}{-p}\)
⇒ \(\frac{\mathrm{p}}{12}\) = \(\frac{3}{p}\) = \(\frac{-\mathrm{p}+3}{-\mathrm{p}}\) ⇒ \(\frac{\mathrm{p}}{12}\) = \(\frac{3}{p}\) = \(\frac{\mathrm{p}-3}{\mathrm{p}}\)
⇒ p × p = 3 × 12
⇒ p² = 36
⇒ p = \(\sqrt{36}\) = 6

Do This

Question 1.
Solve the following systems of equations : (Page No. 79)

i) x – 2y = 0
3x + 4y = 20
Solution:
i) x – 2y = 0
-2y = -x
y = \(\frac{x}{2}\)

3x+ 4y = 20
4y = 20 – 3x
y = \(\frac{20-3 x}{4}\)

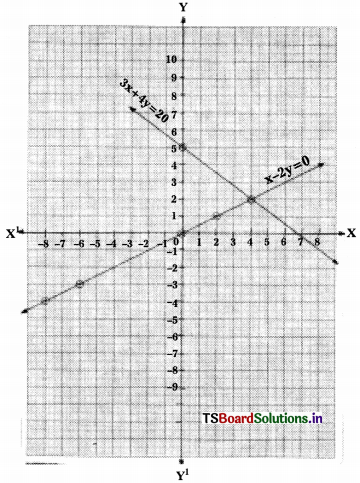
Scale :X-axis – 1 unit = 1 cm
Y – axis – 1 unit = 1 cm

The two lines are intersecting lines, meet at (4, 2).
The solution set is {(4, 2)}.

ii)
x + y = 2
2x + 2y = 4
Solution:
x + y = 2
y = 2 – x

2x + 2y = 4
2y = 4 – 2x
y = \(\frac{4-2 x}{2}\)

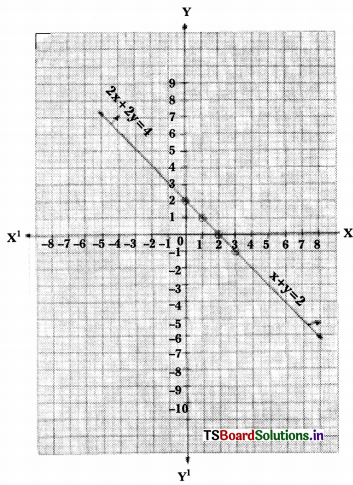
Scale : X – axis – 1 unit = 1 cm
Y – axis – 1 unit = 1 cm

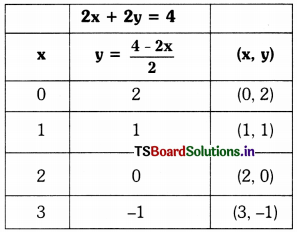
Scale : X – axis – 1 unit = 1 cm
Y – axis – 1 unit = 1 cm
These two lines are coincident lines.
∴ There are infinitely many solutions.

iii) 2x – y = 4; 4x – 2y = 6
Solution:
2x – y = 4 ⇒ y = 2x – 4

4x – 2y = 6 ⇒ 2y = 4x – 6
⇒ y = 2x – 3

These two are parallel lines.
∴ The pair of linear equations has no solution

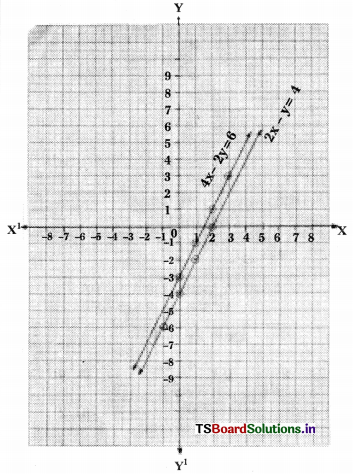
Scale: X – axis – 1 unit = 1 cm
Y – axis – 1 unit = 1 cm

Question 2.
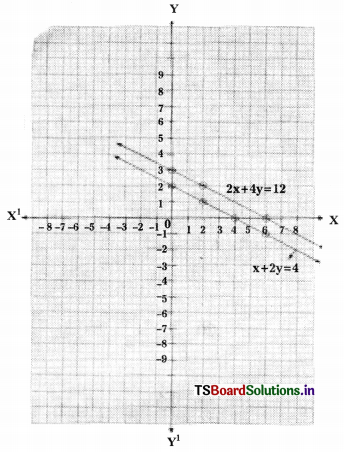
Two rails on a railway track are represented by the equations.
x + 2y – 4 = 0 and 2x + 4y – 12 = 0.
Represent this situation graphically. (Page No. 79)
Solution:
x + 2y – 4 = 0; 2y = 4 – x
y = \(\frac{4-x}{2}\)
x + 2y – 4 = 0

2x + 4y – 12 = 0
⇒ 4y = 12 – 2x ⇒ 4y = 2(6 – x)
⇒ y = \(\frac{6-x}{2}\)

∴ These lines are parallel and hence no solution.

Question 3.
Check each of the given systems of equations to see if It has a unique solution, infinitely many solutions or no solution. Solve them graphically. (A.P. Mar.16’) (Page No. 83)

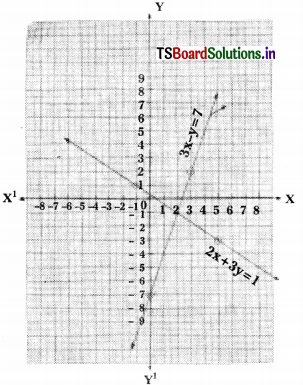
i) 2x + 3y = 1
3x – y = 7
Solution:
Let a₁x + b₁y + c₁ = 0 \(\simeq\) 2x + 3y – 1 = 0
a₂x + b₂y + c₂ = 0 \(\simeq\) 3x – y – 7 = 0
Now comparing their coefficients i.e.,
\(\frac{a_1}{a_2}\) and \(\frac{b_1}{b_2}\) ⇒ \(\frac{2}{3}\) ≠ \(\frac{3}{-1}\)
∴ The given lines are intersecting lines.


Scale: X – axis – 1 unit = 1 cm
Y – axis – 1 unit = 1 cm
2x + 3y = 1
⇒ 3y = 1 – 2x
⇒ y = \(\frac{1-2 x}{3}\)
∴ The system of equation has a unique solution (2, -1).

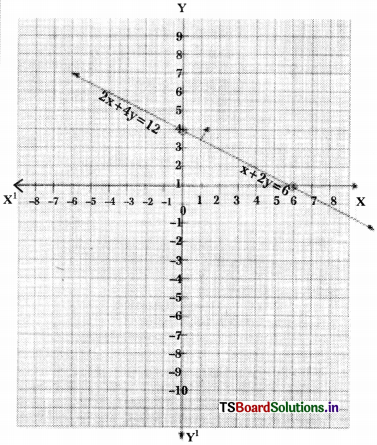
ii) x + 2y = 6
2x + 4y = 12
Solution:
From the given pair of equations,
\(\frac{\mathrm{a}_1}{\mathrm{a}_2}\) = \(\frac{1}{2}\) ; \(\frac{\mathrm{b}_1}{\mathrm{b}_2}\) = \(\frac{2}{4}\) ; \(\frac{\mathrm{c}_1}{\mathrm{c}_2}\) = \(\frac{6}{12}\) = \(\frac{1}{2}\)
∴ \(\frac{\mathrm{a}_1}{\mathrm{a}_2}\) = \(\frac{\mathrm{b}_1}{\mathrm{b}_2}\) = \(\frac{\mathrm{c}_1}{\mathrm{c}_2}\)
∴ The lines are dependent and have infinitely many solutions.
x + 2y = 6 ⇒ 2y = 6 – x
⇒ y = \(\frac{6-x}{2}\)

2x + 4y = 12
⇒ 4y = 12 – 2x ⇒ y = \(\frac{12-2 \mathrm{x}}{4}\)


Scale: X – axis – 1 unit = 1 cm
Y – axis – 1 unit = 1 cm

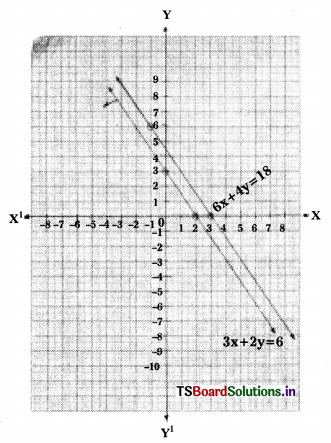
iii) 3x + 2y = 6
6x + 4y = 18
Solution:
From the given equations
\(\frac{\mathrm{a}_1}{\mathrm{a}_2}\) = \(\frac{3}{6}\) = \(\frac{1}{2}\) ; \(\frac{\mathrm{b}_1}{\mathrm{b}_2}\) = \(\frac{2}{4}\) = \(\frac{1}{2}\); \(\frac{\mathrm{c}_1}{\mathrm{c}_2}\) = \(\frac{6}{18}\) = \(\frac{1}{3}\)
∴ \(\frac{\mathrm{a}_1}{\mathrm{a}_2}\) = \(\frac{\mathrm{b}_1}{\mathrm{b}_2}\)
⇒ The lines are parallel and hence no solution.
3x + 2y = 6 ⇒ 2y = 6 – 3x
⇒ y = \(\frac{6-3 x}{2}\)

6x + 4y = 18 ⇒ 4y = 18 – 6x
⇒ y = \(\frac{18-6 \mathrm{x}}{4}\)


Scale : X – axis – 1 unit = 1 cm
Y – axis – 1 unit = 1 cm

Do Thiš

Question 1.
Solve each pair of equations by using the substitution method. (Page No. 88)
i) 3x – 5y = -1
x – y = -1
Solution:
Given: 3x – 5y = -1 —– (1)
x – y = -1 —– (2)
From Equation (2),
x – y = -1
x = y – 1
Substituting x = y – 1 in equation (1), we get
3(y – 1) – 5y = -1
⇒ 3y – 3 – 5y = -1
⇒ -2y = -1 + 3
⇒ 2y = -2
⇒ y = -1
Substituting y = – 1 in equation (1), we get
3x – 5(-1) = -1
3x + 5 = -1
3x = -6
x = -2
∴ The solution is (-2, -1)

ii) x + 2y = -1
2x – 3y = 12
Solution:
Given x + 2y = -1 —- (1)
2x – 3y = 12 —– (2)
From Equation (1), x + 2y = -1
⇒ x = -1 – 2y
Substituting x = -1 – 2y in equation (2), we get
2(-1 – 2y) – 3y = 12
– 2 – 4y – 3y = 12
-2 – 7y = 12
7y = -2 – 12
∴ y = \(\frac{-14}{7}\) = -2
Substituting y = -2 in equation (1), we get
x + 2(-2) = -1
x = -1 + 4
∴ x = 3
∴ The solution is (3, -2).

iii) 2x + 3y = 9
3x + 4y = 5
Solution:
Given : 2x + 3y = 9 —– (1)
3x + 4y = 5 —– (2)
From equation (1),
2x = 9 – 3y
⇒ x = \(\frac{9-3 y}{2}\)
Substituting x = \(\frac{9-3 y}{2}\) in equation (2), we get
3(\(\frac{9-3 y}{2}\)) + 4y = 5
⇒ \(\frac{27-9 y+2 \times 4 y}{2}\) = 5
⇒ 27 – 9y + 8y = 5 × 2
⇒ -y = 10 – 27
∴ y = 17
Substituting y = 17 in equation (1), we get
2x + 3 (+ 17) = 9
⇒ 2x = 9 – 51 ⇒ 2x = -42
⇒ x = -21
∴ The solution is (-21, 17).

iv) x + \(\frac{6}{y}\) = 6
3x – \(\frac{8}{y}\) = 5
Solution:
Given
x + \(\frac{6}{y}\) = 6 —- (1)
3x – \(\frac{8}{y}\) = 5 — (2)
From equation (1), x = 6 – \(\frac{6}{y}\)
Substituting x = 6 – \(\frac{6}{y}\) in equation (2), we get

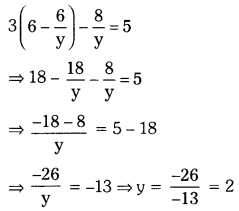
Substituting y = 2 in equation (1), we get
x + \(\frac{6}{2}\) = 6
⇒ x + 3 = 6
∴ x = 3
∴ The solution is (3, 2).

v) 0.2x + 0.3y = 1.3
0.4x + 0.5y = 2.3
Solution:
Given:
0.2x + 0.3y = 1.3 ⇒ 2x + 3y = 13 —- (1)
0.4x + 0.5y = 2.3 ⇒ 4x + 5y = 23 —- (2)
From equation (1),
2x = 13 – 3y = x = \(\frac{13-3 y}{2}\)
Substituting x = \(\frac{13-3 y}{2}\) in equation (2), we get
4(\(\frac{13-3 y}{2}\)) + 5y = 23
⇒ 26 – 6y + 5y = 23
⇒ -y + 26 = 23
⇒ y = 26 – 23 = 3
Substituting y = 3 in equation (1). we get
⇒ 2x + 3(3) = 13
⇒ 2x + 9 = 13
⇒ 2x = 13 – 9
⇒ 2x = 4
⇒ x = 2
∴ The solution is (2, 3).

vi) \(\sqrt{2}\)x + \(\sqrt{3}\)y = 0
\(\sqrt{3}\)x – \(\sqrt{8}\)y = 0
Solution:
Given:
\(\sqrt{2}\)x + \(\sqrt{3}\)y = 0 —–(1)
\(\sqrt{3}\)x – \(\sqrt{8}\)y = 0 —— (2)

∴ The solution is x = 0, y = 0.
Note: a₁x + b₁y + c = 0
a₂x + b₂y + c₂ = 0
then, x = 0, y = 0 is a solution.

Question 2.
Solve each of the following pairs of equations by the elimination method. (Page No. 89)
i) 8x + 5y = 9
3x + 2y = 4
Solution:
Given : 8x + 5y = 9 —- (1)
3x + 2y = 4 —- (2)

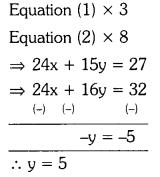
Substituting y = 5 in equation (1), we get
8x + 5 × 5 = 9
⇒ 8x = 9 – 25
x = \(\frac{-16}{8}\)
∴ The solution is (-2, 5).

ii) 2x + 3y = 8
4x + 6y = 7
Solution:
Given: 2x + 3y = 8 —- (1)
4x + 6y = 7 —- (2)

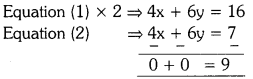
The lines are parallel.
∴ The pair of lines has no solution.

iii) 3x + 4y = 25
5x – 6y = -9
Solution:
Given: 3x + 4y = 25 — (1)
5x – 6y = -9 — (2)

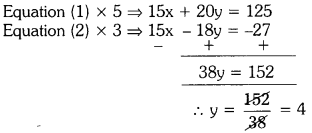
Substituting y = 4 in equation (1), we get
3x + 4 × 4 = 25
3x = 25 – 16
∴ x = \(\frac{9}{3}\) = 3
∴ (3, 4) is the solution for given pair of lines.

Question 3.
In a competitive exam, 3 marks are to be awarded for every correct answer and for every wrong answer, 1 mark will be deducted. Madhu scored 40 marks in this exam. Had 4 marks been awarded for each correct answer and 2 marks deducted for each incorrect answer, Madhu would have scored 50 marks. How many questions were there in the test ? (Madhu attempted all the questions). Use the elimination method. (Page No. 91)
Solution:
The equations formed are
3x – y = 40 — (1)
4x – 2y = 50 — (2)

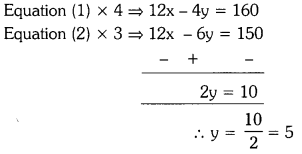
Substituting y = 5 in equation (1), we get
3x – 5 = 40
3x = 40 + 5
x = \(\frac{45}{3}\) = 15
Total number of questions = Number of correct questions + Number of wrong answers
= x + y
= 15 + 5 = 20

Question 4.
Mary told her daughter, Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be. Find the present age of Mary and her daughter. Solve by the substitution method.
(Page No. 92)
Solution:
The Equation formed are
x – 7y + 42 = 0 —- (1)
x – 3y – 6 = 0 — (2)
From (1), x = -42 + 7y
Substituting in equation (2), we get
x = -42 + 7y
⇒ -42 + 7y – 3y – 6 = 0
⇒ 4y – 48 = 0
⇒ y = \(\frac{48}{4}\) = 12
Substituting y = 12 in equation (2), we get
x – 3 × 12 – 6 = 0
x – 36 – 6 = 0
∴ x = 42