TS 10th Class Maths Solutions Chapter 1 Real Numbers Ex 1.5

Students can practice TS 10th Class Maths Solutions Chapter 1 Real Numbers Ex 1.5 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 1 Real Numbers Exercise 1.5

Question 1.
Determine the value of the following.

(i) log₂₅5
Solution:
Let log₂₅5 = x ∵ log_aN = x ⇒ a^x = N
25^x = 5; 5^2x = 5¹ ⇒ a^x = N
⇒ 2x = 1 ⇒ x = \(\frac{1}{2}\)
log₂₅5 = \(\frac{1}{2}\)

(ii) log₈₁3
Solution:
log₈₁3 = x ∵ log<sub.aN = x
81^x = 3 ⇒ (3⁴)^x = 3¹ ⇒ a^x = N
⇒ 4x = 1 ⇒ x = \(\frac{1}{4}\)
log₈₁3 = \(\frac{1}{4}\)

(iii) log₂ \(\left(\frac{1}{16}\right)\)
Solution:
log₂\(\frac{1}{16}\) = x ∵ log_aN = x ⇒ a^x = N
⇒ Then 2^x = \(\frac{1}{16}\) ⇒ 2^x = \(\frac{1}{2^4}\) = 2^-4
⇒ x = – 4
los₂(\(\frac{1}{16}\)) = -4

(iv) log₇1
Solution:
log₇1 = x ∵ log_aN = x ⇒ a^x = N
⇒ Then 7^x = 1 ⇒ 7^x – 7⁰ ⇒ x = 0
⇒ log₁a = 0

(v) log_x \(\sqrt{x}\)
Solution:
log_x \(\sqrt{x}\) ∵ log_aN = x ⇒ a^x = N
⇒ Then x^y = \(\sqrt{x}\) ⇒ x^y = x^1/2
⇒ y = \(\frac{1}{2}\)
log_x \(\sqrt{x}\) = \(\frac{1}{2}\)

(vi) log₂512
Solution:
log₂ 512 ∵ log_aN = x ⇒ a^x = N
⇒ Then 2^x = 512 ⇒ 2^x = 2⁹
⇒ x = 9
log₂512 = 9

(vii) log₁₀0.01
Solution:
log₁₀0.01 = x ∵ log_aN = x ⇒ a^x = N
Then 10^x = 0.01
⇒ 10^x = 10^-2
⇒ x = -2
log₁₀0.01 = -2

(viii) \(\log _{\frac{2}{3}}\left(\frac{8}{27}\right)\)
Solution:
\(\log _{\frac{2}{3}}\left(\frac{8}{27}\right)\) ∵ log_aN = x ⇒ a^x = N
\(\left(\frac{2}{3}\right)^x\) = \(\frac{8}{27}\)
\(\left(\frac{2}{3}\right)^2\) = \(\left(\frac{2}{3}\right)^3\) ⇒ x = 3
\(\log _{\frac{2}{3}}\left(\frac{8}{27}\right)\) = 3

(ix) \(2^{2+\log _2^3}\)
Solution:
\(2^{2+\log _2^3}\) ∵ \(a^{\log _a^m}\) = m
= 2² × \(2^{\log _2^3}\)
= 4 × 3 = 12

Question 2.
Write the following expressions as log N and find their values.

(i) log 2 + log 5
Solution:
log 2 + log 5
∵ log x + log y = log xy
log 2 + log 5 = log (2 × 5)
= log (2 × 5)
= log 10

(ii) log 16 – log 2
Solution:
log 16 – log 2
∵ log x – log y = log \(\left(\frac{x}{y}\right)\)
log 16 – log 2 = log \(\left(\frac{16}{2}\right)\) = log 8

(iii) 3 log 4
Solution:
3 log 4
∵ m log_ax = log_ax^m
3 log 4 = log 4³ = log 64

(iv) 2 log 3 – 3 log 2
Solution:
2 log 3 – 3 log 2 ∵ m log a = log a^m
log x – log y = log\(\frac{x}{y}\)

log 3² – log 2³
log \(\frac{3^2}{2^3}\) = log \(\frac{9}{8}\)

(v) log 243 + log 1
Solution:
log 243 + log 1 ∵ log x + log y = log xy
= log 243 × 1
= log 243

(vi) log 10 + 2 log 3 – log 2
Solution:
log 10 + 2 log 3 – log 2
= log 10 + log 3² – log 2
= log 10 + log 9 – log 2
= log 90 – log 2
= log \(\frac{90}{2}\) = log 45

Question 3.
Evaluate each of the following in terms of x and y, if it is given that x = log₂3 and y = log₂5
(i) log₂ 15
(ii) log₂ 7.5
(iii) log₂60
(iv) log₂6750
Solution:

Question 4.
Expand the following.

(i) log 1000
Solution:

= 3 log 2 + 3 log 5
= 3 [log 2 + log 5]

(ii) log₂\(\left(\frac{128}{625}\right)\)
Solution:
log \(\left(\frac{128}{625}\right)\)

(iii) log x²y³z⁴
Solution:
log x²y³z⁴
= log x² + log y³ + log z⁴
= 2 log x + 3 log y + 4 log z

(iv) log \(\frac{p^2 q^3}{r}\)
Solution:
log \(\frac{p^2 q^3}{r}\)
log (p²q³) – log r
= log p² + log q³ – log r
= 2 log p + 3 log q – log r

(v) \(\log \sqrt{\frac{x^3}{y^2}}\)
Solution:
log \(\sqrt{\frac{x^3}{y^2}}\) ∵ log x^m = m log x
= log \(\left(\frac{x^3}{y^2}\right)^{1 / 2}\) = \(\frac{1}{2} \log \left(\frac{x^3}{y^2}\right)\)
= \(\frac{1}{2}\)[log x³ – log y²]
= \(\frac{1}{2}\)[3 log x – 2 log y]

Question 5.
If x² + y² = 25xy, then prove that 2 log(x + y) = 3log3 + logx + logy.
Solution:
Given x² + y² = 25xy
Adding ‘2xy’ on both sides.
x² + y² + 2xy = 25xy + 2xy
(x + y)² = 27xy
Applying ‘log’ on both sides
log(x + y)² = log 27xy
2log(x + y) = log(3³ × x × y)
= log3³ + log x + log y
∴ 2log(x + y) = 31og3 + logx + logy

Question 6.
If log\(\left(\frac{x+y}{3}\right)\) = \(\frac{1}{2}\)log(x + y) = 3log3 + logx + logy.
Solution:

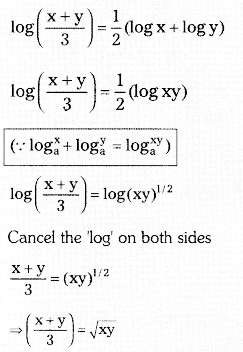
Squaring on both sides

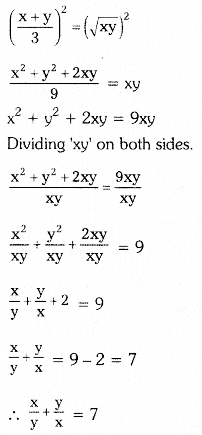
Question 7.
If (2.3)^x = (0.23)^y = 1000, then find the value of \(\frac{1}{x}\) – \(\frac{1}{y}\).
Solution:
Given : (2.3)^x = (0.23)^y = 1000
(2.3)^x = 1000 = 10³
∴ 2.3 = \(10^{\frac{3}{x}}\)
Also (0.23)^y = 10³
∴ 0.23 = \(10^{\frac{3}{y}}\)
Now 0.23 = \(\frac{2.3}{10}\)

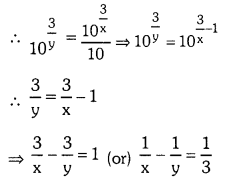
Question 8.
If 2^x+1 = 3^1-x then find the value of x.
Solution:
Given : 2^{x + 1} = 3^{1 – x}
Taking log on b.t.s
log 2^{x + 1} = log 3^{1 – x}
(x + 1) log 2 = (1 – x) log 3
x log 2 + log 2 = log 3 – x log 3
x log 2 + x log 3 = log 3 – log 2
x (log 3 + log 2) = log 3 – log 2
∴ x = \(\frac{\log 3-\log 2}{\log 3+\log 2}\) = \(\frac{\log \frac{3}{2}}{\log 6}\)

Question 9.
Is (i) log 2 rational or irrational? Justify your answer.
(ii) log 100 rational or irrational? Justify your answer.
Solution:
i) log2 is rational. Since the value of log₁₀2
= 0.3010

(ii) log 100 rational or irrational? Justify your answer.
Solution:
log 100 is rational
∴ log₁₀100 = log₁₀10²
= 2 log₁₀10 = 2