TS Inter 2nd Year Maths 2A Solutions Chapter 2 De Moivre’s Theorem Ex 2(b)

Students must practice this TS Intermediate Maths 2A Solutions Chapter 2 De Moivre’s Theorem Ex 2(b) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2A Solutions Chapter 2 De Moivre’s Theorem Exercise 2(b)

I.
Question 1.
Find all the values of
i) (1 – i√3)^1/3
ii) (- i)^1/6
iii) (1 + i)^2/3
iv) (- 16)^1/4
v) (- 32)^1/5
Solution:
z = 2^1/3 \(\left(\frac{1}{2}-\frac{i \sqrt{3}}{2}\right)^{1 / 3}\)
= 2^1/3 \(\left[\cos \frac{\pi}{3}-i \sin \frac{\pi}{3}\right]^{1 / 3}\)
= 2^1/3 \(\left(\cos \frac{\pi}{9}-i \sin \frac{\pi}{9}\right)\)
General solution be = 2^1/3 cis (6k – 1) \(\frac{\pi}{9}\), k = 0, 1, 2, ……………

ii) (- i)^1/6

iii) z = (1 + i)^2/3

iv) z = (- 16)^1/4
= (2) [(- 1)]^1/4
= (2) [cos 2nπ + π) + i sin (2nπ + π)]^1/4
= 2 [cis (2n + 1)π]^1/4
= 2 [cis (2n + 1) \(\frac{\pi}{5}\)]

v) z = (- 32)^1/5
z = 2 (- 1)^1/5
= 2 [cos (2n + 1)π + i sin (2n + 1)π]^1/5
= 2 [cis (2n+ 1) \(\frac{\pi}{5}\)].

Question 2.
If ABC arc angles of a triangle such that x = cis A, y = cis B, z = cis C then find the value of xyz.
Solution:
A + B + C = π
Now xyz = e^iA . e^iB . e^iC
= e^{i(A + B + C)}
= e^i(π)
cos π + i sin π
xyz = – 1 + 0

Question 3.
i) If x = cis θ then find the value of (x⁶ + \(\frac{1}{x^6}\))
ii) Find cube roots of 8.
Solution:
i) x⁶ = e^iθ
\(\frac{1}{x^6}\) = e^{– 6iθ}
x⁶ + \(\frac{1}{x^6}\) = e^iθ + e^{– 6θi}
= cos 6θ + i sin 6θ + cos 6θ – isin 6θ
= 2 cos 6θ.

ii) x = (8)^1/3
x³ – 8 = 0
(x – 2) (x² + 2x + 4)
x = 2, x = \(\frac{-2 \pm \sqrt{4-16}}{2}\)
x = \(\frac{-2 \pm 2 \sqrt{3} \mathbf{i}}{2}\)
x = – 1 ± √3i
Roots are 2, 2ω, 2ω².

Question 4.
If 1, ω, ω² are cube roots of unity, then prove that
i) \(\frac{1}{2+\omega}+\frac{1}{1+2 \omega}=\frac{1}{1+\omega}\)
ii) (2 – ω) (2 – ω²) (2 – ω¹⁰) (2 – ω¹¹) = 49
iii)(x + y + z) (x + yω + zω) (x + yω + zω) = x³ + y³ + z³ – 3xyz
Solution:
\(\frac{1}{2+\omega}+\frac{1}{1+2 \omega}=\frac{1}{1+\omega}\)

ii) (2 – ω) (2 – ω²) (2 – ω¹⁰) (2 – ω¹¹) = 49
L.H.S = (4 – 2(ω + ω²) + ω³) (4 – 2 (ω¹⁰ + ω¹¹) + ω²¹)
= (4 – 2 (- 1) + 1) (4 – 2 (ω + ω²) + (ω³)⁷)
= (7) (4 + 2 + 1) = 49.

iii) (x + y + z) (x + yω + zω) (x + yω + zω) = x³ + y³ + z³ – 3xyz
LH.S = (x + y + z) (x + yω + zω²) (x + yω² + zω)
= [x² + xyω + xzω + yx + y2ω + yzω2 + zx + zyω + z2ω] (x + yω + zω)
= [x + xy(1 + ω) + yz (ω + ω²) + zx (w² + 1) + z² (ω²) + y²ω] (x + yω² + zω)
= [x³ + x²y (1 + ω) + xyz(- 1) + zx²(1 + ω²) + z²xω² + xy²ω + yx²ω² + 2ω(- ω) – y²zω² – xyz + z²yω + y³ + x²zω – zxy – yz²ω – z²xω² + z³ + zy²ω²]
= x³ + y³ + z³ – 3xyz.

Question 5.
Prove that – ω and – ω² are roots of z² – z + 1 = 0 where ω and ω² are the complex cube roots of unity.
Solution:
z² – z + 1 = 0
z = \(\frac{1 \pm \sqrt{1-4}}{2}\)
z = \(\frac{1 \pm \sqrt{3} i}{2}\)
z = \(\frac{-[-1 \mp \sqrt{3} i]}{2}\)
z = – ω, – ω²

Question 6.
If 1, ω, ω² are the cube roots of unity, then find the values of the following.:
i) (a + b)³ + (aω + bω²)³ + (aω² + bω)³
ii) (a + 2b)² + (aω² + 2bω)² + (aω + 2bω²)²
iii) (1 – ω + ω²)³
iv) (1 – ω) (1 – ω²) (1 – ω⁴) (1 – ω⁸)
v) \(\left(\frac{a+b \omega+c \omega^2}{c+a \omega+b \omega^2}\right)+\left(\frac{a+b \omega+c \omega^2}{b+c \omega+a \omega^2}\right)\)
vi) (1 + ω)³ + (1 + ω²)³
viij (1 – ω + ω²)⁵ + (1 + ω – ω²)⁵
Solution:
i)(a + b)³ + (aω + bω²)³ + (aω² + bω)³
= a³ + b³ + 3a²b + 3ab² + a³ω³ + b³ω⁶ + 3a²ω² . bω² + 3aω . b²ω⁴ + a³ω⁶ . b³ω³ + 3a²bω⁴ . ω + 3b²ω² . aω²
= a³ + b³ . 3a²b (1 + ω + ω) + a³ + b³ + 3b²a (ω² + ω + 1) + a³ . b³
= 3 (a³ + b³)

ii) (a + 2b)² + (aω² + 2bω)² + (aω + 2bω²)²
= a² + 4b² + a²ω⁴ + 4b²ω² + 4abω³ + a²ω² + 4b²ω⁴ + 4abω³
= a² (1 + ω + ω²) + 4b² (1 + ω² + ω) + 4ab (1 + ω + ω²)
= 12ab

iii) (1 – ω + ω²)³
Now, 1 + ω + ω² = 0
1 + ω² = – ω
= (- ω – ω)³
= (- 2)³ ω³
= – 8.

iv) (1 – ω) (1 – ω²) (1 – ω⁴) (1 – ω⁸)
= (1 – ω – ω² + ω³) (1 – ω) (1 – ω²)
= (1 – ω – ω² + ω³) (1 – ω – ω² + ω³)
= (1 + 1 + 1) (1 + 1 + 1)
=9

v) \(\left(\frac{a+b \omega+c \omega^2}{c+a \omega+b \omega^2}\right)+\left(\frac{a+b \omega+c \omega^2}{b+c \omega+a \omega^2}\right)\)
= \(\frac{\omega^2\left(a+b \omega+c \omega^2\right)}{\left(c \omega^2+a \omega^3+b \omega^4\right)}+\frac{\left(a \omega^2+b \omega^3+c \omega^4\right)}{\omega^2\left(b+c \omega+a \omega^2\right)}\)
= ω² + \(\frac{1}{\omega^2}\)
= ω² + \(\frac{\omega}{\omega^3}\)
= ω² + ω = – 1

vi) (1 + ω)³ + (1 + ω²)³
= (- ω²)³ + (- ω)³
= – 1 + (- 1) = – 2.

vii) (1 – ω + ω²)⁵ + (1 + ω – ω²)⁵
1 + ω² = – ω
= (- 2ω)⁵ + (- 2ω²)⁵
= (- 2)⁵ (ω² + ω)
= (- 2)⁵ (- 1) = 32.

II. Question 1.
Solve the following equations.
i) x⁴ – 1 = 0
ii) x⁵ + 1 = 0
iii) x⁹ – x⁵ + x⁴ – 1 = 0
iv) x⁴ + 1 = 0
Solution:
i) x⁴ – 1 = 0
(x² – 1) (x² + 1) = 0
(x – 1) (x + 1) (x – i) (x + i) = 0
x = 1, – 1, i, – i.

ii) x⁵ = – 1
x = (- 1)^1/5
x = [cos (2n + 1) π + i sin (2n + 1) π]^1/5 n = 0, 1, 2, 3, 4
= cos(2n + 1) \(\frac{\pi}{5}\) + i sin(2n + 1) \(\frac{\pi}{5}\)

iii) x⁹ – x⁵ + x⁴ – 1 = 0
x⁵ (x⁴ – 1) + (x⁴ – 1) = 0
(x⁴ – 1) (x⁵ + 1) = 0
(x – 1) (x + 1) (x – i) (x + 1) (x⁵ + 1) = 0
x = ± 1, ± i, cis (2n + 1) \(\frac{\pi}{5}\).

iv) x⁴ + 1 = 0
x = (- 1)^1/4
x = [cos (2n + 1)π + isin(2n + 1)π]^1/4
x = cos (2n + 1)\(\frac{\pi}{4}\) + i sin(2n + 1)\(\frac{\pi}{4}\)
n = 0, 1, 2, 3.

Question 2.
Find the common roots of x¹² – 1 = 0 and x⁴ + x² + 1 = 0.
Solution:
x¹² – 1 = 0
(x⁴)³ – 1 = o
(x⁴ – 1) [x⁸ – x⁴ + 1] = 0
(x – 1) (x + 1) (x – i) (x + i) (x⁸ + x⁴ + 1) = 0 (or)
x = (1)^1/12
x = [cos 2nπ + i sin2nπ]^1/12 n = 0, 1, 2, …………. 11 ……………(1)
x⁴ + x² + 1 = 0
(x² – 1) (x⁴ + x² + 1) = 0
x⁶ – 1 = 0
x = (1)^1/6
x = [cos 2nπ + i sin 2nπ]^1/6
= \(\cos \frac{2 n \pi}{6}+i \sin \frac{2 n \pi}{6}\), n = 0, 1, 2, 3, 4, 5 …………..(2)
Common roots to (1) and (2)
cis \(\frac{\pi}{3}\), cis \(\frac{2 \pi}{3}\), cis \(\frac{4 \pi}{3}\), cis \(\frac{5 \pi}{3}\).

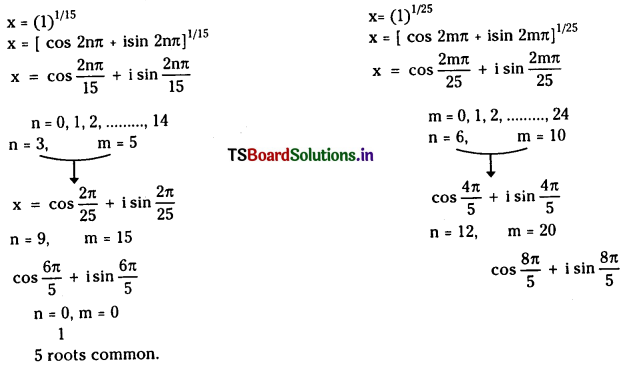
Question 3.
Find the number of 15th roots of unity, which are also 25th roots of unity.
Solution:

Question 4.
If the cube roots of unity are 1, ω, ω, then find the roots of the equation (x – 1)3 + 8 = 0.
Solution:
(x – 1)³ = – 8
(x – 1) = (- 8)^1/3
x – 1 = – 2
x – 1 = – 2ω
x – 1 = – 2ω²
∴ x = – 1
x = – 2ω + 1
x = – 2ω² + 1

Question 5.
Find the roduct of all values of (1 + i)\(\frac{4}{5}\).
Solution:

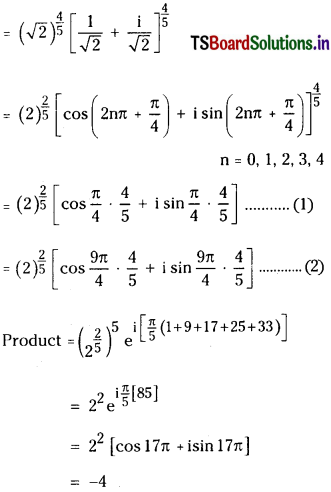
Question 6.
If z² + z + 1 = 0, where z is a complex number, prove that
\(\left(z+\frac{1}{z}\right)^2+\left(z^2+\frac{1}{z^2}\right)^2+\left(z^3+\frac{1}{z^3}\right)^2\) + \(\left(z^4+\frac{1}{z^4}\right)^2+\left(z^5+\frac{1}{z^5}\right)^2+\left(z^6+\frac{1}{z^6}\right)^2\) = 12.
Solution:
z = ω satisfy
L.H.S = \(\left(z+\frac{1}{z}\right)^2+\left(z^2+\frac{1}{z^2}\right)^2+\left(z^3+\frac{1}{z^3}\right)^2\) + \(\left(z^4+\frac{1}{z^4}\right)^2+\left(z^5+\frac{1}{z^5}\right)^2+\left(z^6+\frac{1}{z^6}\right)^2\)
= (- 1)² + (- 1)² + (2)² + (- 1)² + (- 1)² + (2)² = 12.

III.
Question 1.
1, α, α², α³, ……………. α^{n – 1} be the nth roots of unity then prove that 1^p + α^p + (α²)^p + (α³)^p + ………….. + (α^{n – 1})^p = {0 if p ≠ kn, n if p = kn. where p, k ∈ N.
Solution:
Now xⁿ – 1 = 0
x = (1)^1/n
x = [cos 2nπ + i sin 2nπ]^1/n
x = \(\cos \frac{2 m \pi}{n}+i \sin \frac{2 m \pi}{n}\)
α = \(\cos \frac{2 m \pi}{n}+i \sin \frac{2 m \pi}{n}\)
α^p = \(\cos \frac{2 m p \pi}{n}+i \sin \frac{2 m p \pi}{n}\)
Now p = kn
1 + 1 + 1 + …………. nterms = n
If p ≠ kn value then1^p + α^p + (α²)^p + (α³)^p + ………….. + (α^{n – 1})^p = 0.

Question 2.
Prove the sum of 99th powers of the roots of the equation x⁷ – 1 = 0 is zero and hence deduce the roots of x⁶ + x⁵ + x⁴ + x³+ x² + x + 1 = 0.
Solution:
x⁷ – 1 = 0
x = (1)^1/7
x = (cos 2kπ + sin 2kπ)^1/7
k = 0, 1, 2, ………., 6
x₁ = 1, x₂ = \(e^{\frac{2 \pi}{7} i}\), x₂ = \(e^{\frac{4 \pi}{7} i}\), x₃ = \(e^{\frac{6 \pi}{7} i}\), ………….. x₆ = \(\frac{12 \pi}{7} \mathrm{i}\)
x₁⁹⁹ + x₂⁹⁹ + x₃⁹⁹ + …………..
1⁹⁹ + \(\mathrm{e}^{\frac{2 \pi}{7} \cdot 99 \mathrm{i}}+\mathrm{e}^{\frac{4 \pi}{7} \cdot 99 \mathrm{i}}+\ldots \ldots . \mathrm{e}^{\frac{12 \pi}{7} \cdot 99 \mathrm{i}}\) = 0
Roots of x⁶ + x⁵ + x⁴ + x³+ x² + x + 1 = 0 be \(\cos \frac{2 k \pi}{7}+i \sin \frac{2 k \pi}{7}\); k = 1, 2, 3, 4, 5, 6.
∵ (x⁷) – 1 = (x – 1) (x⁶ + x⁵ + x⁴ + x³+ x² + x + 1) = 0
x = 1 is one root
⇒ cis \(\frac{2 k \pi}{7}\); k = 1, 2, 3, 4, 5, 6.

Question 3.
If n is a positive integer, show that (P + iQ)^1/n + (P – iQ)^1/n = 2 (P² + Q²)^1/2n cos(\(\frac{1}{n}\) tan^-1 \(\frac{Q}{P}\))
Solution:
P = r cos θ
Q = r sin θ
(P + iQ)^1/n = [r cos θ + i sin θ]^1/n
= r^1/n \(\left[\cos \frac{\theta}{n}+i \sin \frac{\theta}{n}\right]\)
(P – iQ)^1/n = [r cos θ – i sin θ]^1/n
= r^1/n \(\left[\cos \frac{\theta}{n}-i \sin \frac{\theta}{n}\right]\)
(P + iQ)^1/n + (P – iQ)^1/n = r^1/n [2 cos \(\frac{\theta}{n}\)]
= 2r^1/n cos \(\frac{\theta}{n}\)
Now P² + Q² = r²
r = (P² + Q²)^1/2
tan θ = \(\frac{Q}{P}\); θ = tan^-1 \(\frac{Q}{P}\)
= 2 (P² + Q²)^1/2n cos(\(\frac{1}{n}\) tan^-1 \(\frac{Q}{P}\)).

Question 4.
Show that one value of \(\left[\frac{1+\sin \frac{\pi}{8}+i \cos \frac{\pi}{8}}{1+\sin \frac{\pi}{8}-i \cos \frac{\pi}{8}}\right]^{\frac{8}{3}}\) is – 1.
Solution:
\(\left[\frac{1+\cos \left(\frac{\pi}{2}-\frac{\pi}{8}\right)+i \sin \left(\frac{\pi}{2}-\frac{\pi}{8}\right)}{1+\cos \left(\frac{\pi}{2}-\frac{\pi}{8}\right)-i \sin \left(\frac{\pi}{2}-\frac{\pi}{8}\right)}\right]^{\frac{8}{3}}\)

= \(\left[\frac{2 \cos ^2 \frac{3 \pi}{16}+2 i \sin \frac{3 \pi}{16} \cos \frac{3 \pi}{16}}{2 \cos ^2 \frac{3 \pi}{16}-2 i \sin \frac{3 \pi}{16} \cos \frac{3 \pi}{16}}\right]^{\frac{8}{3}}\)

= \(\left[\frac{\cos \frac{3 \pi}{16}+i \sin \frac{3 \pi}{16}}{\cos \frac{3 \pi}{16}-i \sin \frac{3 \pi}{16}}\right]^{\frac{8}{3}}\)

= \(\frac{\mathrm{e}^{\frac{\mathrm{i} \pi}{2}}}{\mathrm{e}^{\frac{-\mathrm{i} \pi}{2}}}\) = e^iπ = – 1.

Question 5.
Solve (x – 1)ⁿ = xⁿ, n is a positive integer.
Solution: