TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(e)

Students must practice this TS Intermediate Maths 2B Solutions Chapter 1 Circle Ex 1(e) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Exercise 1(e)

I.

Question 1.
Discuss the relative position of the following pair of circles.
(i) x² + y² – 4x – 6y – 12 = 0, x² + y² + 6x + 18y + 26 = 0
Solution:
Let S ≡ x² + y² – 4x – 6y – 12 = 0 ……..(1) and S’ ≡ x² + y² + 6x + 18y + 26 = 0 ……..(2) be the given circles.
The Centre of the circle (1) is C₁ = (2, 3)
Centre of circle (2) is C₂ = (-3, -9)
Radius of circle (1) is \(\sqrt{4+9+12}\) = 5 = r₁
Radius of circle (2) is \(\sqrt{9+81-26}\) = 8 = r₂
Now C₁C₂ = \(\sqrt{(2+3)^2+(3+9)^2}\) = 13
and r₁ + r₂ = 5 + 8 = 13
Since C₁C₂ = r₁ + r₂, the two circles touched each other externally.

(ii) x² + y² + 6x + 6y + 14 = 0, x² + y² – 2x – 4y – 4 = 0
Solution:
Taking S ≡ x² + y² + 6x + 6y + 14 = 0 ……….(1) and S’ ≡ x² + y² – 2x – 4y – 4 = 0 ………(2)
The Centre of the circle (1) is C₁1 = (-3, -3)
and the Centre of the circle (2) is C₂ = (1, 2)
Radius of circle (1) is r₁ = \(\sqrt{9+9-14}\) = 2
Radius of circle (2) is r₂ = \(\sqrt{1+4+4}\) = 3
Now C₁C₂ = \(\sqrt{(1+3)^2+(2+3)^2}\) = √41
r₁ + r₂ = 5
Since C₁C₂ > r₁ + r₂, each circle lies on the exterior of the other circle.

(iii) (x – 2)² + (y + 1)² = 9, (x + 1)² + (y – 3)² = 4
Solution:
The equation of the given circles are
(x – 2)² + (y + 1)² = 9 ………(1)
(x + 1)² + (y – 3)² = 4 ……….(2)
Centre of circle (1) is C₁ = (2, -1)
The Centre of the circle (2) is C₂ = (-1, 3)
The radius of the circle (1) is r₁ = 3
The radius of the circle (2) is r₂ = 2
C₁C₂ = \(\sqrt{(2+1)^2+(-1-3)^2}\) = 5
and r₁ + r₂ = 3 + 2 = 5
∴ Since C₁C₂ = r₁ + r₂, the two circles touch each other externally.

(iv) x² + y² – 2x + 4y – 4 = 0, x² + y² + 4x – 6y – 3 = 0
Solution:
Given equations of circles are
x² + y² – 2x + 4y – 4 = 0 ……….(1)
x² + y² + 4x – 6y – 3 = 0 ……….(2)
Centre of circle (1) is C₁ = (1, -2)
The Centre of the circle (2) is C₂ = (-2, 3)
Radius of circle (1) is r₁ = \(\sqrt{1+4+4}\) = 3
Radius of circle (2) is r₂ = \(\sqrt{4+9+3}\) = 4
Distance between centres C₁C₂ = \(\sqrt{(1+2)^2+(-2-3)^2}=\sqrt{9+25}=\sqrt{34}\)
r₁ + r₂ = 3 + 4 = 7 and |r₁ – r₂| = |3 – 4| = 1
∴ |r₁ – r₂| < C₁C₂ < r₁ + r₂
∴ The two given circles (1) and (2) intersect each other in two points.

Question 2.
Find the number of possible common tangents that exist for the following pairs of circles.
(i) x² + y² + 6x + 6y + 14 = 0, x² + y² – 2x – 4y – 4 = 0
Solution:
The given equations of circles are
x² + y² + 6x + 6y + 14 = 0 ………(1)
and x² + y² – 2x – 4y – 4 = 0 ……..(2)
Centre of circle (1) is C₁ = (-3, -3)
The Centre of the circle (2) is C₂ = (1, 2)
Radius of circle (1) is r₁ = \(\sqrt{9+9-14}\) = 2
Radius of circle (2) is r₂ = \(\sqrt{1+4+4}\) = 3
C₁C₂ = \(\sqrt{(-3-1)^2+(-3-2)^2}=\sqrt{16+25}\) = √41
and r₁ + r₂ = 2 + 3 = 5
Since C₁C₂ > r₁ + r₂ the given circles do not intersect each other.
The number of possible common tangents that can be drawn to the above circles is ‘4’.

(ii) x² + y² – 4x – 2y + 1 = 0, x² + y² – 6x – 4y + 4 = 0
Solution:
The given equations of circles are
x² + y² – 4x – 2y + 1 = 0 ………(1)
and x² + y² – 6x – 4y + 4 = 0 ……….(2)
The Centre of the circle (1) is C₁ = (2, 1)
The Centre of the circle (2) is C₂ = (3, 2)
Radius of circle (1) is r₁ = \(\sqrt{4+1-1}\) = 2
Radius of circle (2) is r₂ = \(\sqrt{9+4-4}\) = 3
C₁C₂ = \(\sqrt{(2-3)^2+(1-2)^2}=\sqrt{1+1}=\sqrt{2}\)
and r₁ + r₂ = 2 + 3 = 5
∴ |r₁ – r₂| = |2 – 3| = 1
∴ |r₁ – r₂| < C₁C₂ < r₁ + r₂
∴ The two given circles intersect each other in two points.
The number of possible common tangents that can be drawn to the circles is ‘2’.

(iii) x² + y² – 4x + 2y – 4 = 0, x² + y² + 2x – 6y + 6 = 0
Solution:
The given equations of circles are
x² + y² – 4x + 2y – 4 = 0 ……….(1)
and x² + y² + 2x – 6y + 6 = 0 …………(2)
Centre of circle (1) is C₁ = (2, -1)
The Centre of the circle (2) is C₂ = (-1, 3)
Radius of circle (1) is r₁ = \(\sqrt{4+1+4}\) = 3
Radius of circle (2) is r₂ = \(\sqrt{1+9-6}\) = 2
C₁C₂ = \(\sqrt{(2+1)^2+(-1-3)^2}=\sqrt{9+16}\) = 5
and r₁ + r₂ = 3 + 2 = 5
Since C₁C₂ = r₁ + r₂, the two circles touch externally and the number of possible common tangents is ‘3’.

(iv) x² + y² = 4, x² + y² – 6x – 8y + 16 = 0
Solution:
The equations of given circles are x² + y² = 4 ………(1) and x² + y² – 6x – 8y + 16 = 0 ……….(2)
The Centre of the circle (1) is C₁ = (0, 0)
The Centre of the circle (2) is C₂ = (3, 4)
The radius of the circle (1) is r₁ = 2
Radius of circle (2) is r₂ = \(\sqrt{9+16-16}\) = 3
C₁C₂ = \(\sqrt{9+16}\) = 5 = r₁ + r₂
Hence the two circles touch externally and the number of possible common tangents is ‘3’.’

(v) x² + y² + 4x – 6y – 3 = 0, x² + y² + 4x – 2y + 4 = 0
Solution:
The equations of circles are
x² + y² + 4x – 6y – 3 = 0 ……….(1)
and x² + y² + 4x – 2y + 4 = 0 ……….(2)
The Centre of the circle (1) is C₁ = (-2, 3)
The Centre of the circle (2) is C₂ = (-2, 1)
Also radius of circle are r1 = \(\sqrt{4+9+3}\) = 4
Radius of circle (2) are r2 = \(\sqrt{4+1-4}\) = 1
Now C₁C₂ = \(\sqrt{(-2+2)^2+(3-1)^2}\) = 4
and |r₁ – r₂| = |4 – 1| = 3
∴ C₁C₂ < |r₁ + r₂|, one circle lies completely inside the other circle.
∴ The number of common tangents that can be drawn to the circles S = 0 and S’ = 0 is zero.

Question 3.
Find the internal centre of similitude of the circles x² + y² + 6x – 2y + 1 = 0 and x² + y² – 2x – 6y + 9 = 0.
Solution:
Equations of given circles are
x² + y² + 6x – 2y + 1 = 0 ……….(1)
x² + y² – 2x – 6y + 9 = 0 ……….(2)
The Centre of the circle (1) is C₁ = (-3, 1)
The Centre of the circle (2) is C₂ = (1, 3)
Also radius of circle (1) is r₁ = \(\sqrt{9+1-1}\) = 3
radius of circle (2) is r₂ = \(\sqrt{1+9-9}\) = 1
Now C₁C₂ = \(\sqrt{(-3-1)^2+(1-3)^2}=\sqrt{16+4}\) = √20
and r₁ + r₂ = 3 + 1 = 4
Since C₁C₂ > r₁ + r₂, the two circles do not touch or do not intersect each other but each circle lies in the exterior of the other.
∴ Number of common tangents = 4
Both internal and external centres of similitude exist.

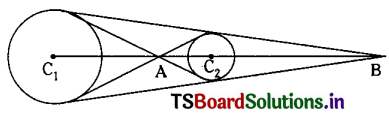
Let A be the internal centre of similitude and r₁ : r₂ = 3 : 1.
∴ A divides \(\overline{\mathrm{C}_1 \mathrm{C}_2}\) in the ratio 3 : 1 internally.

∴ The internal centre of similitude is (0, \(\frac{5}{2}\))

Question 4.
Find the external centre of similitude for the circles x² + y² – 2x – 6y + 9 = 0, x² + y² = 4.
Solution:
The equations of given circles are x² + y² – 2x – 6y + 9 = 0 ……..(1) and x² + y² = 4 ……..(2)
Centre of circles are C₁ = (1, 3) and C₂ = (0, 0)
Radius of circles are r₁ = \(\sqrt{1+9-9}\) = 1 and r₂ = √4 = 2
Now C₁C₂ = \(\sqrt{1+9}=\sqrt{10}\) and r₁ + r₂ = 1 + 2 = 3
Since C₁C₂ > r₁ + r₂, each circle lies in the exterior of the other circle, and the number of common tangents = 4
∴ Both internal and external centres of similitudes do exist in this case.
C₁ = (1, 3) = (x₁, y₁) and C₂ = (0, 0) = (x₂, y₂)

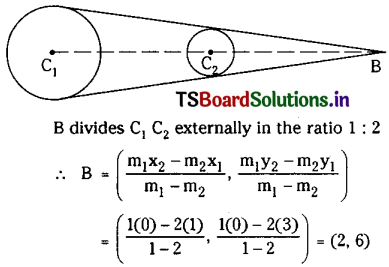
∴ The external centre of the similitude of the circle is (2, 6).

II.

Question 1.
(i) Show that the circles x² + y² – 6x – 2y + 1 = 0, x² + y² + 2x – 8y + 13 = 0 touch each other. Find the point of contact and the equation of the common tangent at their point of contact. (Mar. ’11, ’10, ’09)
Solution:
Let S = x² + y² – 6x – 2y + 1 = 0 and S’ = -x² + y² + 2x – 8y + 13 = 0 be the given circles.
The centre of circles are C₁ = (3, 1) and C₂ = (-1, 4)
Radius of circles are r₁ = \(\sqrt{9+1-1}\) = 3 and r₂ = \(\sqrt{1+16-13}\) = 2
Distance between centres C₁C₂ = \(\sqrt{(3+1)^2+(1-4)^2}=\sqrt{16+9}\) = 5 and r₁ + r₂ = 3 + 2 = 5
Since C₁C₂ = r₁ + r₂, the two circles touch externally at a point.

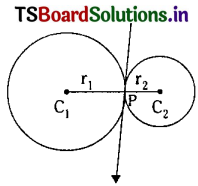
Let P be the point of contact of circles such that r₁ : r₂ = 3 : 2.
Since P divides C₁, C₂ internally in the ratio 3 : 2,
the coordinates of the point of contact

The equation of common tangent is S – S’ = 0
⇒ x² + y² – 6x – 2y + 1 – x² – y² – 2x + 8y + 13 = 0
⇒ -8x + 6y – 12 = 0
⇒ 4x – 3y + 6 = 0
∴ The equation of the common tangent at the point of contact is 4x – 3y + 6 = 0.

(ii) Show that x² + y² – 6x – 9y + 13 = 0, x² + y² – 2x – 16y = 0 touch each other. Find the point of contact and the equation of the common tangent at their point of contact.
Solution:
Given equations of circles are S = x² + y² – 6x – 9y + 13 = 0 and S’ = x² + y² – 2x – 16y = 0
Centre of circles are C₁ = (3, \(\frac{9}{2}\)) and C₂ = (1, 8)

The point P divides C₁C₂ externally in the ratio of their radius \(\frac{\sqrt{65}}{2}\) : √65 = 1 : 2

The equation of the common tangent at P(5, 1) to the circles S = 0 and S’ = 0 is S – S’ = 0.
⇒ x² + y² – 6x – 9y + 13 – x² – y² + 2x + 16y = 0
⇒ -4x + 7y – 13 = 0
⇒ 4x – 7y + 13 = 0
∴ The equation of the required common tangent is 4x – 7y + 13 = 0.

Question 2.
Find the equation of the circle which touches the circle x² + y² – 2x – 4y – 20 = 0 externally at (5, 5) with radius ‘5’.
Solution:

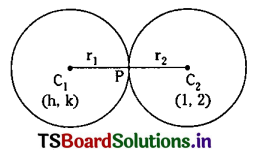
Let C₁ = (h, k) be the centre and r1 be the radius of the required circle.
Given r₁ = 5
Equation of the given circle is x² + y² – 2x – 4y – 20 = 0 ……….(1)
Centre of the circle C₂ = (1, 2) and radius r₂ = \(\sqrt{1+4+20}\) = 5
∴ r₁ : r₂ = 5 : 5 = 1 : 1
Point P(5, 5) divides C₁C₂ in the ratio 1 : 1 internally.
∴ \(\left(\frac{\mathrm{h}+1}{2}, \frac{\mathrm{k}+2}{2}\right)\) = (5, 5)
⇒ \(\frac{\mathrm{h}+1}{2}\) = 5 and \(\frac{\mathrm{k}+2}{2}\) = 5
⇒ h = 9 and k = 18
∴ C1 = (h, k) = (9, 8)
∴ The equation of a required circle with centre (9, 8) and radius ‘5’ is (x – 9)² + (y – 8)² = 25
⇒ x² + y² – 18x – 16y + 120 = 0

Question 3.
Find the direct common tangents of the circles x² + y² + 22x – 4y – 100 = 0 and x² + y² – 22x + 4y + 100 = 0. (New Model Paper)
Solution:
Let S = x² + y² + 22x – 4y – 100 = 0 ……….(1) and S’ = x² + y² – 22x + 4y + 100 = 0 …….(2) be the given circles.
Then centres of the circles are C₁ = (-11, +2) and C₂ = (11, -2)
The radius of the circles are

and r₁ + r₂ = 15 + 5 = 20
Since C₁C₂ > r₁ + r₂, the two circles are such that each lies on the exterior of the other.
Hence both internal and external centre of similitude exists.

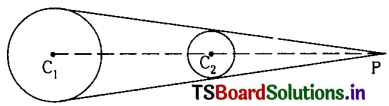
Now r₁ : r₂ = 15 : 5 = 3 : 1
Point P divides C₁, C₂ externally in the ratio of radii 3 : 1.

The equation of direct common tangent passing through (22, -4) having slope ‘m’ is y + 4 = m(x – 22)
⇒ mx – y – 4 – 22m = 0 …….(1)
Since the line is tangent to S’ = 0.
Perpendicular distance from C₂ = (11, -2) to the line (1) = radius of the circle S’ = 0
∴ \(\left|\frac{m(11)+2-4-22 m}{\sqrt{m^2+1}}\right|\) = 5
⇒ \(\left|\frac{-(11 m+2)}{\sqrt{m^2+1}}\right|\) = 5
⇒ (11m + 2)² = 25(m² + 1)
⇒ 121m² + 44m + 4 = 25m² + 25
⇒ 96m² + 44m – 21 = 0
⇒ 96m² + 72m – 28 m – 21 = 0
⇒ 24m(4m + 3) – 7(4m + 3) = 0
⇒ (24m – 7) (4m + 3) = 0
⇒ m = \(\frac{-3}{4}\) or m = \(\frac{7}{24}\)
∴ Equations of direct common tangents from (1) are y + 4 = \(\frac{-3}{4}\)(x – 22)
⇒ 4y + 16 = -3x + 66
⇒ 3x + 4y – 50 = 0
and y + 4 = \(\frac{7}{24}\)(x – 22)
⇒ 24y + 96 = 7x – 154
⇒ 7x – 24y – 250 = 0
∴ The equations of direct common tangents are given by 3x + 4y – 50 = 0 and 7x – 24y – 250 = 0.

Question 4.
Find the transverse common tangents of the circles x² + y² – 4x – 10y + 28 = 0 and x² + y² + 4x – 6y + 4 = 0.
Solution:
Let S = x² + y2 – 4x – 10y + 28 = 0 ………(1)
S’ = x² + y2 + 4x – 6y + 4 = 0 ……….(2)
be the given circles.
Centres of the circles are C₁ = (2, 5) and C₂ = (-2, 3)
Also, the radius of circles are r₁ = \(\sqrt{4+25-28}\) = 1 and r₂ = \(\sqrt{4+9-4}\) = 3
Also C₁C₂ = \(\sqrt{(2+2)^2+(5-3)^2}\) = √20 = 2√5 and r₁ + r₂ = 4
Since C₁C₂ > r₁ + r₂, we have each circle lying in the exterior of other circles.
Hence we get 2 direct common tangents and 2 transverse common tangents that can be drawn.

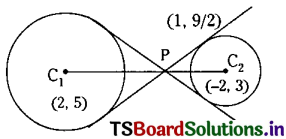
Point P divides C₁C₂ internally in the ratio r₁ : r₂ = 1 : 3.
Let P be the internal centre of similitude.

Let the equation of transverse common tangent be y – \(\frac{9}{2}\) = m(x – 1) ……(1)
⇒ 2y – 9 = 2mx – 2m
⇒ 2mx – 2y + (9 – 2m) = 0 ……….(2)
Since line (2) is a tangent to the circle S = 0, the perpendicular distance from C₁ (2, 5) to line (2) is equal to the radius of the circle S = 0.
∴ \(\left|\frac{2 m(2)-2(5)+9-2 m}{\sqrt{4 m^2+4}}\right|\) = 1
⇒ |2m – 1| = \(2 \sqrt{m^2+1}\)
⇒ 4m² – 4m + 1 = 4(m² + 1)
⇒ 4m² – 4m + 1 – 4m² – 4 = 0
⇒ -4m – 3 = 0
⇒ m = \(\frac{-3}{4}\)
∴ Equation of tangent is y – \(\frac{9}{2}\) = \(\frac{-3}{4}\)(x – 1)
⇒ \(\frac{2 y-9}{2}=-\frac{3}{4}(x-1)\)
⇒ 2(2y – 9) = -3(x – 1)
⇒ 4y – 18 = -3x + 3
⇒ 3x + 4y – 21 = 0
Since the m² term is canceled, the slope of one of the transverse common tangents is not defined.
One transverse common tangent is passing through P(1, \(\frac{9}{2}\)) and parallel to y-axis.
∴ The equation of other transverse common tangents is x = 1.
∴ The equations of transverse common tangents are x = 1 and 3x + 4y – 21 = 0.

Question 5.
Find the pair of tangents from (4, 10) to the circle x² + y² = 25.
Solution:
Let P(x₁, y₁) be the given point.
The equation to the pair of tangents drawn from P(4, 10) to S = 0 is \(\mathrm{S}_1^2=\mathrm{SS}_{11}\).
Given S = x² + y² – 25 = 0
(xx₁ + yy₁ – 25)² = (x² + y² – 25) (\(x_1^2+y_1^2\) – 25)
⇒ (4x + 10y – 25)² = (x² + y² – 25) (16 + 100 – 25)
⇒ (4x + 10y – 25)² = (x² + y² – 25) (91)
⇒ 16x² + 100y² + 625 + 80xy – 500y – 200x = 91x² + 91y² – 2275
⇒ 75x² – 9y² – 80xy + 200x + 500y – 2900 = 0

Question 6.
Find the pair of tangents drawn from (0, 0) to x² + y² + 10x + 10y + 40 = 0.
Solution:
Let P(x₁, y₁) be the given point.
The equation to the pair of tangents drawn from P(0, 0) to S = 0 is \(\mathrm{S}_1^2=\mathrm{SS}_{11}\).
Given S = x² + y² + 10x + 10y + 40 = 0
∴ The equation to the pair of tangents from (0, 0) to S = 0 is [xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c]² = (x² + y² + 2gx + 2fy + c) (\(x_1^2+y_1^2\) + 2gx₁ + 2fy₁ + c)
⇒ (5x + 5y + 40)² = (x² + y² + 10x + 10y + 40) (40)
⇒ 25x² + 25y² + 1600 + 50xy + 400xy + 400x = 40(x² + y² + 10x + 10y + 40)
⇒ 15x² + 15y² – 50xy = 0
⇒ 3x² + 3y² – 10xy = 0

III.

Question 1.
Find the equation of the circle which touches x² + y² – 4x + 6y – 12 = 0 at (-1, 1) internally with a radius of ‘2’.
Solution:
The given circle is x² + y² – 4x + 6y – 12 = 0
The centre of the circle is (2, -3) and radius = \(\sqrt{4+9+12}\) = 5
Let the centre of the required circle be (h, k), and given that 2 is the radius with the point of contact of circles internally as (-1, 1).
Suppose (x₁, y₁) = (2, -3), (x₂, y₂) = (h, k), r₁ = 5, r₂ = 2
point of contact (x, y) = (-1, 1)
using the formula for the external division since two circles touch internally.

⇒ (5x – 1)² + (5y – 3)² = 100
⇒ 25x² + 25y² – 10x – 30y – 90 = 0
⇒ 5x² + 5y² – 2x – 6y – 18 = 0

Question 2.
Find all common tangents of the following pairs of circles.
(i) x² + y² = 9 and x² + y² – 16x + 2y + 49 = 0
Solution:
Let S = x² + y² – 9 = 0 and S’ = x² + y² – 16x + 2y + 49 = 0 be the given circles.
Centre of the circle S = 0 is C₁ (0, 0) and radius = 3
Centre of the circle S’ = 0 is C₂ (8, -1) and radius r2 = \(\sqrt{64+1-49}\) = 4
r₁ + r₂ = 3 + 4 = 7 and C₁C₂ = \(\sqrt{64+1}=\sqrt{65}\) > 7
Since C₁C₂ > r₁ + r₂ we get each circle lies completely in the exterior of the other.
∴ Two direct and two transverse common tangents can be drawn to S = 0 and S’ = 0.
r₁ : r₂ = 3 : 4
Let A be the internal centre of similitude and A divides C₁C₂ in the ratio 3 : 4 internally

⇒ 64x² + y² + 441 – 16xy + 42y – 336x = 16(x² + y² – 9)
⇒ 48x² – I6xy – 15y² + 42y – 336x + 585 = 0
⇒ 48x² – 36xy + 20xy – 15y² + 42y – 336x + 585 = 0
⇒ 12x(4x – 3y) + 5y(4x – 3y) + 42y – 336x + 585 = 0
⇒ (12x + 5y)(4x – 3y) – 336x + 42y + 585 = 0
Let 48x² – 16xy – 15y² + 42y – 336x + 585 = (12x + 5y + l) (4x – 3y + m)
= 48x² – 36xy + 12mx + 20xy – 15y² + 5ym + 4lx + 3ly + lm
= 48x² – 16xy – 15y² + (4l + 12m)x + (-3l + 5m)y + lm
Equating coefficients of x, y, and the constant term
4l + 12m = -336
⇒ l + 3m = -84 ………(1)
-3l + 5m = 42
⇒ 3l – 5m = -42 ……..(2)
and lm = 585 …….(3)
From (1), 5l + 15m = -420
From (2), 9l – 15m = -126
∴ 14l = -546
⇒ l = -39
From (1), -39 + 3m = -84
⇒ 3m = -45
⇒ m = -15
∴ 48x² – 16xy – 15y² + 42y – 336x + 585 = (12x + 5y – 39) (4x – 3y – 15)
∴ The transverse common tangents are 12x + 5y – 39 = 0 and 4x – 3y – 15 = 0
Let B be the external centre of the similitude of circles.
∴ B divides C1C2 in the ratio 3 : 4 externally
∴ B = \(\left(\frac{3(8)-4(0)}{3-4}, \frac{3(-1)-4(0)}{3-4}\right)\) = (-24, 3)
The equation is the pair of direct common tangents to the circle S = 0 from (-24, 3) is \(S_1^2=S S_{11}\)
⇒ [x(-24) + y(3) – 9]² = (x² + y² – 9) (576 + 9 – 9)
⇒ (-24x + 3y – 9)² = (576) (x² + y2 – 9)
⇒ 9(-8x + y – 3)² = 9 × 64 (x² + y2 – 9)
⇒ (-8x + y – 3)² = 64(x² + y2 – 9)
⇒ 64x² + y² + 9 – 16xy – 6y + 48x = 64x² + 64y² – 576
⇒ 63y² + 16xy – 48x + 6y – 585 = 0
⇒ y(63y + 16x) – 48x + 6y – 585 = 0
∴ 63y² + 16xy – 48x + 6y – 585 = (y + l) (63y + 16x + m)
Equating coefficients of x, y, and constants
16l = 48 ……..(4)
63l + m = 6 ………(5)
lm = -585 ……….(6)
∴ l = -3 and from (6), m = 195
∴ 63y² + 16xy – 48x + 6y – 585 = (y – 3) (63y + 16x + 195)
∴ The equations of direct common tangents to the circles S = 0, S’ = 0 are y – 3 = 0, 63y + 16x + 195 = 0.
Hence equations of all common tangents to the circles S = 0 and S’ = 0 are 4x – 3y – 15 = 0, 12x + 5y – 39 = 0 and y – 3 = 0, 16x + 63y + 195 = 0.

(ii) x² + y² + 4x + 2y – 4 = 0 and x² + y² – 4x – 2y + 4 = 0
Solution:
Let S = x² + y² + 4x + 2y – 4 = 0 and S’ = x² + y² – 4x – 2y + 4 = 0
Centre of S = 0 is C₁ (-2, 1) and the radius is r₁ = \(\sqrt{4+1+4}\) = 3
Centre of S’ = 0 is C₂ (2, 1) and the radius r₂ = \(\sqrt{4+1-4}\) = 1
Also C₁C₂ = \(\sqrt{(2+2)^2+(1+1)^2}=\sqrt{16+4}\) = √20 = 2√5 and r₁ + r₂ = 3 + 1 = 4
Since C₁C₂ > r₁ + r₂, each circle lies in the exterior of the other circle.
∴ Two direct and two transverse common tangents can be drawn to the circles S = 0 and S’ = 0.
Let A, B be the internal and external centres of similitudes of circles S = 0 and S’ = 0
A divides \(\overline{\mathrm{C}_1 \mathrm{C}_2}\) in the ratio r₁ : r₂ = 3 : 1 internally
∴ A = \(\left(\frac{m_1 x_2+m_2 x_1}{m_1+m_2}, \frac{m_1 y_2+m_2 y_1}{m_1+m_2}\right)\)


⇒ -(2x + y – 1)² = (x² + y² + 4x + 2y – 4)
⇒ (2x + y – 1)² = (x² + y² + 4x + 2y – 4)
⇒ 4x² + y² + 1 + 4xy – 2y – 4x = x² + y² + 4x + 2y – 4
⇒ 3x² + 4xy – 8x – 4y + 5 = 0
⇒ x(3x + 4y) – 8x – 4y + 5 = 0
⇒ 3x² + 4xy – 8x – 4y + 5 = (x + l) (3x + 4y + m)
Comparing the coefficients of x, y, and constants
3l + m = -8 ………(1)
4l = -4 ……….(2)
lm = 5 ……….(3)
∴ From (2), l = -1 and From (3), m = -5
∴ 3x² + 4xy – 8x – 4y + 5 = (x – 1) (3x + 4y – 5)
The equations of transverse common tangents are x – 1 = 0, 3x + 4y – 5 = 0.
The equation of pair of direct common tangents to the circle S = 0 is \(\mathrm{s}_1^2=\mathrm{S} \mathrm{S}_{11}\).
⇒ [x(4) + y(2) + 2(x + 4) + 1(y + 2) – 4]² = (x² + y² + 4x + – 2y – 4) (16 + 4 + 16 + 4 – 4)
⇒ (6x + 3y + 6)² = (x² + y² + 4x + 2y – 4)(36)
⇒ 9(2x + y + 2)² = 36(x² + y² + 4x + 2y – 4)
⇒ (2x + y + 2)² = 4(x² + y² + 4x + 2y – 4)
⇒ 4x² + y² + 4 + 4xy + 4y + 4x = 4x² + 4y² + 16x + 8y – 16
⇒ 3y² – 4xy + 8x + 4y – 20 = 0
⇒ y(3y – 4x) + 8x + 4y – 20 = 0
∴ 3y² – 4xy + 8x + 4y – 20 = (y + l) (3y – 4x + m)
Comparing coefficients of x, y, and constants we get
-4l = 8 ………(4)
3l + m = 4 ………(5)
lm = -20 ………(6)
From (4), l = -2 and from (6), m = 10
∴ 3y² – 4xy + 8x + 4y – 20 = (y – 2) (3y – 4x + 10)
Hence the equations of direct common tangents are y – 2 = 0, 3y – 4x + 10 = 0.
∴ The equations of all common tangents to the circles S = 0, S’ = 0 are x – 1 = 0, 3x + 4y – 5 = 0 and y – 2 = 0, 4x – 3y – 10 = 0

Question 3.
Find the pair of tangents drawn from (3, 2) to the circle x² + y² – 6x + 4y – 2 = 0.
Solution:
Let S ≡ x² + y² – 6x + 4y – 2 = 0 be the given circle.
The equation of pair of tangents drawn from (3, 2) to the circle S = 0 is \(S_1^2=S . S_{11}\)
⇒ [x(3) + y(2) – 3(x + 3) + 2(y + 2) – 2]² = (x² + y² – 6x + 4y – 2) (3² + 2² – 18 + 8 – 2)
⇒ (4y – 7)² = 1 . (x² + y² – 6x + 4y – 2)
⇒ 16y² – 56y + 49 = x² + y² – 6x + 4y – 2
⇒ x² – 15y² – 6x + 60y – 51 = 0

Question 4.
Find the pair of tangents drawn from (1, 3) to the circle x² + y² – 2x + 4y – 11 = 0 and also find the angle between them.
Solution:
Denote S ≡ x² + y² – 2x + 4y – 11 = 0
The equation of pair of tangents from (1, 3) to the circle S = 0 is by the formula \(S_1^2=S . S_{11}\)
⇒ [x(1) + y(3) – (x + 1) + 2(y + 3) – 11]² = (x² + y² – 2x + 4y – 11) (1² + 3² – 2 + 12 – 11)
⇒ (5y – 6)² = (x² + y² – 2x + 4y – 11) (9)
⇒ 25y² – 60y + 36 = 9x² + 9y² – 18x + 36y – 99
⇒ 9x² – 16y² – 18x + 96y – 135 = 0
If θ is the angle between the above pair of tangents to S = 0, then

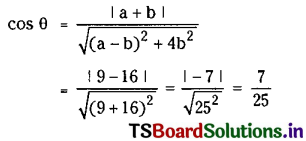
(or) θ = \(\cos ^{-1}\left(\frac{7}{25}\right)\) is the angle between pair of tangents to S = 0.

Question 5.
Find the pair of tangents from the origin to the circle x² + y² + 2gx + 2fy + c = 0 and hence deduce a condition for these tangents to the perpendicular.
Solution:
Let S ≡ x² + y² + 2gx + 2fy + c = 0 be the given circle.
Then the equation of the pair of tangents drawn from (0, 0) to S = 0 is by the formula \(S_1^2=S . S_{11}\)
⇒ [x(0) + y(0) + g(x + 0) + f(y + 0) + c]² = (x² + y² + 2gx + 2fy + c) (c)
⇒ (gx + fy + c)² = cx² + cy² + 2gcx + 2fcy + c²
⇒ (g²x² + f²y² + c² + 2fgxy + 2fcy + 2cgx) = cx² + cy² + 2gcx + 2fcy + c²
⇒ x²(g² – c) + y²(f² – c) + 2fgxy = 0
Given that pair of tangents represented by this equation are perpendicular we have
coefficient of x² + coefficient of y² = 0
⇒ g² – c + f² – c = 0
⇒ g² + f² = 2c

Question 6.
From a point on the circle x² + y² + 2gx + 2fy + c = 0 two tangents are drawn to the circle x² + y² + 2gx + 2fy + c sin²α + (g² + f²) cos²α = 0 (0 < α < π/2). Prove that the angle between them is 2α.
Solution:
Let S = x² + y² + 2gx + 2fy + c = 0 and S’ = x² + y² + 2gx + 2fy + c sin²α + (g² + f²) cos²α = 0 be the given circles.
Let P(x₁, y₁) be any point on S = 0 then

Let θ be the angle between the tangents drawn from P(x₁, y₁) to S’ = 0 then

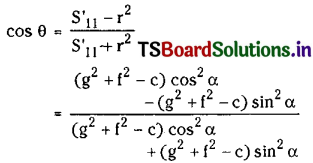
= \(\frac{\left(g^2+f^2-c\right)\left(\cos ^2 \alpha-\sin ^2 \alpha\right)}{\left(g^2+f^2-c\right)\left(\cos ^2 \alpha+\sin ^2 \alpha\right)}\)
= cos 2α
∴ cos θ = cos 2α ⇒ θ = 2α
∴ The angle between the tangents drawn from P(x1, y1) to the circle S’ = 0 is 2α.