Students can practice TS 6th Class Maths Solutions Chapter 4 Basic Geometrical Ideas InText Questions to get the best methods of solving problems.
TS 6th Class Maths Solutions Chapter 4 Basic Geometrical Ideas InText Questions
Do This
Question 1.
Four points are marked in the given rectangle. Name them.

Answer:
Their names taken as P, Q, R, S.

Question 2.
Take a geo-board. Select any two nails and tie tightly a thread from one end to the other. The thread you have fixed is a line which can extend in both directions and only in these two directions.
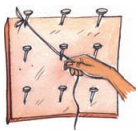
Answer:
Student activity
Think: Discuss And Write
Question 1.
Here is a ray \(\overrightarrow{\mathrm{O A}}\). It starts at O and passes through the points A and B.
Can you name ray \(\overrightarrow{\mathrm{O A}}\) as \(\overrightarrow{\mathrm{O B}}\)? Why?
![]()
Can you write the ray \(\overrightarrow{\mathrm{O A}}\) as \(\overrightarrow{\mathrm{A O}}\) ? Why ? Give reasons.
Answer:

The above ray starts from the point ‘O’ towards B so, it is named as \(\overrightarrow{\mathrm{O B}}\).
\(\overrightarrow{\mathrm{OA}} \neq \overrightarrow{\mathrm{AO}}\) since the ray starts from 0 i.e., it should be represented by only \(\overrightarrow{\mathrm{O A}}\).
![]()
Think. Discuss And Write
Question 1.
Move your pencil along the following English letters and state which are open and which are closed?

Answer:
D and O are closed letters
G, L, M are open letters.
Question 2.
Tell which letter is an example of simple curve.
Answer:
O is an example of simple curve.
Try These
Question 1.
Identify which are simple curves and which are not?

Answer:
(i) and(ii) are simple curves.
(iii) and (iv) are not simple curves.
Do This
Question 1.
Take some match sticks and try to make simple figures. Identify closed figures in them.
Answer:
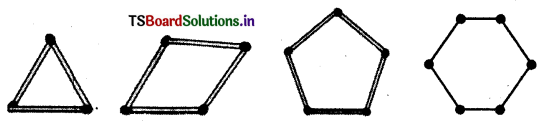
Question 2.

What is the least number of sticks needed to form a closed figure ? Obviously three. Can you explain why two match sticks can not make a closed figure.
Answer:
Minimum number of sticks that are needed to form a closed figure are 3. If we take less than 3 sticks it will become a open figure.
Question 3.
Take some straw pieces of diffrent size. Pass thread into any 3 pieces and make different triangles. Draw figures for the tiangles in your notebook.
Answer:
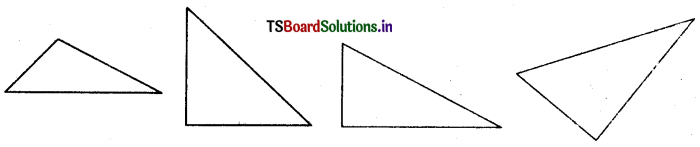
Think, Discuss And Write
Question 1.
Take four points A, B, C and D such that A, B, C lie on the same line and D is not on it. Can the four line segments \(\overline{\mathrm{A B}}, \overline{\mathrm{B C}}, \overline{\mathrm{C D}}\) and \(\overline{\mathrm{AD}}\) form a quadrilateral? Give reason.
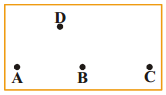
Answer:
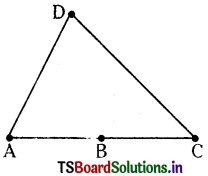
No, the given four line segments \(\overline{\mathrm{A B}}, \overline{\mathrm{B C}}, \overline{\mathrm{C D}}\) and \(\overline{\mathrm{AD}}\)
Can not form a quadrilateral.
To form a quadrilateral maximum two points should be collinear.
![]()
Do This
Question 1.
Draw a circle on a paper and cut ¡t along its edge. Fold it Into half and again fold it to one fourth to make folding marks as shown.

You will observe a point in the middle. Mark this O. This is the centre of the circle. You can also indicate its radius. How many radii can you draw in a circle ?
Answer:
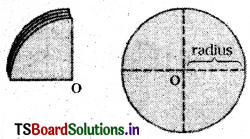
Infinite number of radii we can draw in a circle.
Because infinite number of points are there on the circumference of the circle.
Question 2.
Draw a circle and draw at least 5 chords in it. Make sure at least one of them passes through the centre. Name them and fill the table.
| S.No. | Chord | Length | Passes through the centre (Yes/No) |
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 |
What do you notice?
Answer:
| S.No | Chord | Length | Passes through the centre (Yes/No) |
| 1 | AB | 5 | Yes |
| 2 | CD | 2 | No |
| 3 | EB | 1.5 | No |
| 4 | GH | 2.7 | No |
| 5 | FT | 2 | No |
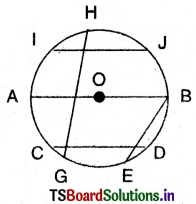
I notice that a chord which passes through the centre of the circle is the largest chord of all the chords.
![]()
Think And Discuss
Question 1.
Is it possible to draw more than one diameter in a circle ? Are all the diameters equal in length ? Discuss with your friends and find the answer.
Answer:
We can draw infinite number of diameters in a circle.

All the lengths of diameters are equal in a circle.
Since \(\overline{\mathrm{AF}}=\overline{\mathrm{BG}}=\overline{\mathrm{CH}}\) = 2.5 cm