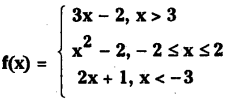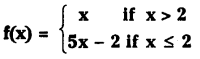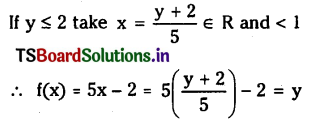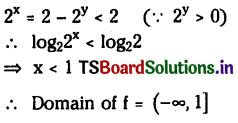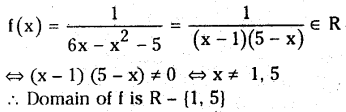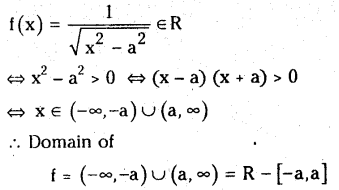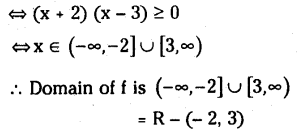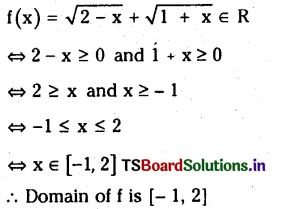obul

Solving these TS 10th Class Maths Bits with Answers Chapter 1 Real Numbers Bits for 10th Class will help students to build their problem-solving skills.

Real Numbers Bits for 10th Class

Question 1.
\(\sqrt{4}\) is
A) a rational number
B) an irrational number
C) an odd number
D) none of these
Answer:
A) a rational number

Question 2.
The logarithmic form of 64 = 2⁶ is
A) log₂64 = 6
B) log₆64 = 2
C) log₄64 = 2
D) log₃64 = 6
Answer:
A) log₂64 = 6

Question 3.
The exponential form of \(\log _4 1024\) = 5 is = 5 is
A) 5⁴ =1024
B) 6⁴ = 1024
C) 4⁵ = 1024
D) 2⁸ = 1024
Answer:
C) 4⁵ = 1024

Question 4.
If log₂8 = y, then y =
A) 3
B) 4
C) 6
D) 10
Answer:
A) 3

Question 5.
log₃729 = x, then x =
A) 243
B) 81
C) 9
D) 6
Answer:
D) 6

Question 6.
log 15 =
A) log 1 + log 5
B) log 10 + log 5
C) log 3 + log 5
D) log 3 × log 5
Answer:
C) log 3 + log 5

Question 7.
The HCF of the least prime number and the least composite number is
A) 1
B) 3
C) 4
D) 2
Answer:
A) 1

Question 8.
The L.C.M of 36 and 54 is
A) 18
B) 108
C) 36
D) 54
Answer:
B) 108

Question 9.
The sum of the exponents of the prime factor in the prime factorisation of 108 is
A) 5
B) 6
C) 4
D) 1
Answer:
A) 5

Question 10.
\(1 . \overline{23}\) is
A) a rational number
B) an irrational number
C) an integer
D) a natural number
Answer:
A) a rational number

Question 11.
The HCF of 6, 72 and 120 is
A) 12
B) 15
C) 6
D) 3
Answer:
C) 6

Question 12.
The LCM of 8, 9 and 25 is
A) 200
B) 1800
C) 225
D) 72
Answer:
B) 1800

Question 13.
The rational number in between and \(\sqrt{1}\) and is
(A) \(\frac{9}{4}\)
(B) \(\frac{3}{4}\)
(C) \(\frac{5}{4}\)
(D) \(\frac{5}{4}\)
Answer:
(B) \(\frac{3}{4}\)

Question 14.
Set of Rational and irrational numbers are called
A) Real numbers
B) Natural numbers
C) Whole numbers
D) Integers
Answer:
A) Real numbers

Question 15.
log form of 3⁵ = 243 is …..
A) \(\log _3^{243}\) = 5
B) \(\log _5^{243}\) = 3
C) \(\log _3^{243}\) = 5
D) \(\log _5^{243}\) = 5
Answer:
A) \(\log _3^{243}\) = 5

Question 16.
the symbol of “implies” is ……….
A) ⇔
B) ⇒
C) ∀
D) ∃
Answer:
B) ⇒

Question 17.
The prime factorisation of 729 is ………..
A) 36
B) 35
C) 34
D) 38
Answer:
A) 36

Question 18.
If ‘x’ and ‘y’ are two prime numbers then their HCF
A) 3⁶
B) 3⁵
C) xy
D) x + y
Answer:
B) 3⁵

Question 19.
\(\log _{10}^{0.01}\) = ……..
A) -1
B) 1
C) -2
D) 2
Answer:
C) -2

Question 20.
The number of odd numbers in between O’ and 100 is …. ( )
A) 100
B) 51
C) 49
D) 50
Answer:
D) 50

Question 21.
The exponential form of \(\log _4^8\) = x is …………..
A) x⁸ = 4
B) x⁴ = 8
C) 4^x = 8
D) 8^x = 4
Answer:
C) 4^x = 8

Question 22.
The value of \(\frac{36}{2^3 \times 5^3}\) in decimal form is ………
A) 0.036
B) 0.36
C) 0.0036
D) 3.6
Answer:
A) 0.036

Question 23.
LCM of two numbers is 108 and their HCF is 9 and one of them is 54. So the second one is ( )
A) 9
B) 18
C) 6
D) 12
Answer:
B) 18

Question 24.
The number of prime factors of 36 is
A) 4
B) 3
C) 2
D) 1
Answer:
C) 2

Question 25.
The exponential form of \(\log _{10}^{0.001}\) = – 3 is ……
A) (0.001)¹⁰ = -3
B) (-3)¹⁰ = 0.001
C) 10³ = -0.001
D) 10^-3 = 0.001
Answer:
D) 10^-3 = 0.001

Question 26.
Which of the following in not a rational number …… ( )
A) \(\log _{10}^3\)
B) \(5 . \overline{23}\)
C) 12.123
A) \(\frac{10}{19}\)
Answer:
A) \(\log _{10}^3\)

Question 27.
LCM of 24 and 36 is ……. ( )
A) 24
B) 36
C) 72
D) 864
Answer:
C) 72

Question 28.
H.C.F. of 324 and 360 is …… ( )
A) 9
B) 1
C) 63
D) 36
Answer:
B) 1

Question 29.
\(\log _x \sqrt[3]{x}\) = …… ( )
A) 3
B) \(\frac{1}{3}\)
C) \(0 . \overline{3}\)
D) B and C
Answer:
D) B and C

Question 30.
\(\log _4 8^2\) …………………..
A) 4
B) 8
C) 2
D) 3
Answer:
A) 4

Question 31.
Last digit of 5¹⁰⁰ is ………..
A) 5
B) 6
C) 0
D) Cannot say
Answer:
C) 0

Question 32.
log₁₀0 …….
A) does not exist
B) 1
C) 0
D) exist
Answer:
B) 1

Question 33.
If log 2 = 0.30103, then log 32 = ( )
A) 4.81648
B) 1.50515
C) 9.63296
D) 9.0309
Answer:
A) 4.81648

Question 34.
If log₁₀ 0.00001 = x, then x =
A) 4
B) -4
C) 5
D) -5
Answer:
D) -5

Question 35.
If log_aax² – 5x + 8 = 2, then x = ….
A) 2 or 3
B) 5 or 7
C) -2 or -3
D) 8 or -2
Answer:
D) 8 or -2

Question 36.
log₃x² = 2 then x =
A) 2
B) -2
C) 3
D) -3
Answer:
C) 3

Question 37.
\(\log _9 \sqrt{3 \sqrt{3 \sqrt{3}}}\) = ……….
A) \(\frac{7}{8}\)
B) \(\frac{7}{16}\)
C) \(\frac{7}{16}\)
D) \(\frac{1}{8}\)
Answer:
A) \(\frac{7}{8}\)

Question 38.
log₈128 =
(A) 7/3
(B) 16
(C) 2048
(D) 136
Answer:
(D) 136

Question 39.
Which of the following is an irrational number ? ( )

Answer:
(D) \(\sqrt{25+16}\)

Question 40.
The prime factorization of 144 is ( )
A) 4² × 3²
B) 2⁷ × 3⁴
C) 12 × 12
D) 2⁴ × 3²
Answer:
D) 2⁴ × 3²

Question 41.
L.C.M of the numbers 2⁷ × 3⁴ × 7 and 2³ × 3⁴ × 11 is ( )
A) 2³ × 3⁴
B) 2⁷ × 3⁴
C) 2⁷ × 3⁴ × 7 × 11
D) 2³ × 3⁴ × 7 × 11
Answer:
D) 2³ × 3⁴ × 7 × 11

Question 42.
The H.C.F. of the numbers 3⁷ × 5³ × 2⁴ and 3² × 7⁴ × 2⁸ is
A) 2⁴ × 3²
B) 2⁸ × 3⁷ × 5³ × 7⁴
C) 2⁸ × 3⁷
D) 2 × 3 × 5 × 7
Answer:
C) 2⁸ × 3⁷

Question 43.
The decimal expansion of 0.225 in its rational form is
A) 225
B) \(\frac{225}{10^4}\)
C) \(\frac{225}{10^2}\)
D) \(\frac{9}{40}\)
Answer:
C) \(\frac{225}{10^2}\)

Question 44.
Which of the following is a rational number ?
A) \(\sqrt{3}\)
B) \(\sqrt{5}\)
C) \(\sqrt{7}\)
D) \(\sqrt{9}\)
Answer:
A) \(\sqrt{3}\)

Question 45.
What is the L.C.M of greatest 2 digit num-ber and the greatest 3 digit number ?
A) 99 × 999
B) 999
C) 99 × 9 × 111
D) 9 × 11 × 111
Answer:
B) 999

Question 46.
What is the H.C.F of n and n + 1, where n is a natural number ? ( )
A) n
B) n + 1
C) n/2
D) 1
Answer:
D) 1

Question 47.
What is the L.C.M of least prime and the least composite number ?
A) least prime × least composite
B) 2
C) least composite
D) 6
Answer:
D) 6

Question 48.
The product of L.C.M. and H.C.F. of the least prime and least composite number is ( )
A) 4
B) 6
C) 8
D) 16
Answer:
D) 16

Question 49.
n² – 1 is divisible by 8, if n is ( )
A) an odd number
B) an even number
C) prime number
D) integer
Answer:
B) an even number

Question 50.
If x and y are any two co-primes, then their L.C.M. is ( )
A) x + y
B) x . y
C) x/y
D) x – y
Answer:
C) x/y

Question 51.
If x and y are any two relatively prime numbers, then their H.C.F is ( )
A) x . y
B) x
C) y
D) 1
Answer:
D) 1

Question 52.
If m and n are co-primes, the H.C.F. of m² and n² is ( )
A) m
B) n²
C) m²
D) 1
Answer:
A) m

Question 53.
If n is a natural number, then which of the following expression ends in zero ?
A) (3 × 2)ⁿ
B) (5 × 7)ⁿ
C) (9 × 3)ⁿ
D) (2 × 5)ⁿ
Answer:
A) (3 × 2)ⁿ

Question 54.
The number of prime factors of 72 is
A) 12
B) 2
C) 3
D) 6
Answer:
C) 3

Question 55.
How many prime factors are there in the prime factorization of 240 ? ( )
A) 20
B) 5
C) 3
D) 6
Answer:
B) 5

Question 56.
After how many digits will the decimal expansion of 11/32 terminates ? ( )
A) 5
B) 4
C) 3
D) Never
Answer:
D) Never

Question 57.
p, q are co-primes and q = 2ⁿ.5^m where m > n, then the decimal expansion of p/q terminates after places.
A) m
B) n
C) m . n
D) m + n
Answer:
A) m

Question 58.
The decimal expansion of \(\frac{9}{17}\) is
A) terminating
B) non-terminating & non-repeating
C) non-terminating & repeating
D) none
Answer:
D) none

Question 59.
The decimal expansion of \(\frac{27}{14}\) is ( )
A) \(1 . \overline{9285714}\)
B) \(1.9 \overline{285714}\)
C) 1.9285714
D) \(0.19 \overline{285714}\)
Answer:
A) \(1 . \overline{9285714}\)

Question 60.
\(5.6789 \overline{1}\) is a ……. number ( )
A) prime
B) composite
C) irrational
D) rational
Answer:
C) irrational

Question 61.
0.12112 1112 11112 ….. is …… number
A) irrational
B) rational
C) composite
D) prime
Answer:
C) composite

Question 62.
\(\sqrt{2}\) – 2 is …….. number ( )
A) natural
B) rational
C) whole
D) an irrational
Answer:
D) an irrational

Question 63.
3 × 5 × 7 × 11 + 35 is …… number.
A) composite
B) natural
C) negative
D) none
Answer:
B) natural

Question 64.
The decimal expansion of \(\frac{209}{80}\) terminates after ….. places. ( )
A) 5
B) 6
C) 4
D) 9
Answer:
A) 5

Question 65.
7 × 11 × 17 + 34 is divisible by ………
A) 7 or 10
B) 7 or 19
C) 17 or 79
D) 8 or 231
Answer:
C) 17 or 79

Question 66.
\(\frac{73}{625}\) has a …… decimal expansion.
A) Non-terminal
B) Terminal
C) Non-terminating, repeating
D) None
Answer:
D) None

Question 67.
The number of prime factors of 1024 is ………..
A) 12
B) 9
C) 7
D) 1
Answer:
B) 9

Question 68.
The decimal expansion of \(\frac{199}{99}\) is ……….
A) \(1 . \overline{02}\)
B) \(1 . \overline{07}\)
C) \(1 . \overline{39}\)
D) \(1 . \overline{14}\)
Answer:
D) \(1 . \overline{14}\)

Question 69.
The period of the decimal expansion of \(\frac{19}{21}\) is ……
A) 917461
B) 904761
C) 940761
D) None
Answer:
A) 917461

Question 70.
If a rational number p/q has a terminating decimal, then the prime factorisation q is of the form
A) 3^m5ⁿ
B) 3^m
C) 3^m5ⁿ3^p
D) 2^m5ⁿ
Answer:
C) 3^m5ⁿ3^p

Question 71.
The prime factorisation of 20677 is
A) 13 × 29 × 71
B) 23 × 29 × 31
C) 19 × 23 × 17
D) None
Answer:
C) 19 × 23 × 17

Question 72.
The LCM of 208 and 209 is …..
A) 208 × 109
B) 19 × 218
C) 104 × 20
D) 208 × 209
Answer:
A) 208 × 109

Question 73.
The HCF of 1001 and 1002 is ….
A) 1
B) 7
C) 9
D) 11
Answer:
B) 7

Question 74.
If p₁, p₂, p₃,…… p_n are co-primes then their LCM is …….
A) p₃p₅p₇
B) p₆p₇…. p_n
C) p₁p₂…….. p_n
D) p₂p₄…..p_n
Answer:
C) p₁p₂…….. p_n

Question 75.
In the above problem HCF is ….
A) p₁
B) 9
C) 1
D) 7
Answer:
D) 7

Question 76.
The decimal expansion of \(\frac{7}{16}\) without actual division is …….
A) 0.4375
B) 4.375
C) 43.75
D) 0.0004375
Answer:
C) 43.75

Question 77.
The expansion of \(\frac{87}{625}\) terminates after …. places.
A) 6
B) 4
C) 14
D) 9
Answer:
A) 6

Question 78.
The expansion of \(\frac{123}{125}\) terminates after ……. places.
A) 9
B) 7
C) 3
D) None
Answer:
C) 3

Question 79.
The decimal form of \(\frac{80}{81}\) repeats after …….. places.
A) 16
B) 12
C) 7
D) None
Answer:
D) None

Question 80.
\(\frac{70}{71}\) is a …… decimal.
A) terminating
B) non-terminating
C) non-terminating, repeating
D) none
Answer:
B) non-terminating

Question 81.
\(\frac{123}{125}\) is a … decimal.
A) terminating
B) non-terminating
C) non-terminating, repeating
D) none
Answer:
C) non-terminating, repeating

Question 82.
14.381 may certain the denominator when expressed in p/q form is ….
A) 8³ × 6³
B) 12³ × 4³
C) 2³ × 5³
D) 7³ × 8³
Answer:
C) 2³ × 5³

Question 83.
5\(\sqrt{5}\) + 6\(\sqrt{5}\) – 2 \(\sqrt{5}\) = ……
A) 6 \(\sqrt{5}\)
B) 7 \(\sqrt{5}\)
C) 2 \(\sqrt{5}\)
D) 9 \(\sqrt{5}\)
Answer:
D) 9 \(\sqrt{5}\)

Question 84.
9 \(\sqrt{2}\) × \(\sqrt{2}\) = ……
A) 16
B) 18
C) 19
D) 20
Answer:
D) 20

Question 85.
log₁₀10 = ……………
A) 0
B) -1
C) 1
D) 7
Answer:
D) 7

Question 86.
log_a\(\frac{1}{a}\) = ……
A) 4
B) 3
C) -1
D) 12
Answer:
A) 4

Question 87.
log_ba . log_ab = ……
A) 7
B) 3
C) 4
D) 1
Answer:
A) 7

Question 88.
log₁1 = …………
A) 1
B) -1
C) 0
D) not defined
Answer:
D) not defined

Question 89.
log_0.10.01 = ……..
A) 8
B) 6
C) 9
D) None
Answer:
B) 6

Question 90.
log 2 + log 5 = …….
A) 1
B) 2
C) 9
D) 12
Answer:
A) 1

Question 91.
16 × 64 = 4^k then k = ……..
A) 9
B) 12
C) 5
D) 19
Answer:
C) 5

Question 92.
a + b = b + a is called …….. property.
A) Associative
B) Identity
C) Inverse
D) Commutative
Answer:
B) Identity

Question 93.
log₅125 = ……..
A) 5
B) 3
C) 15
D) 12
Answer:
C) 15

Question 94.
Exponential form of log₄64 = 3 is ……..
A) 4³ = 64
B) 3⁴ = 64
C) 4² = 81
D) None
Answer:
A) 4³ = 64

Question 95.
log 15 = ……..
A) log 5 + log 10
B) log 3 + log 12
C) log 5 + log 3
D) all the above
Answer:
D) all the above

Question 96.
\(\frac{1}{\sqrt{2}}\) is a ………. number.
A) rational
B) an irrational
C) natural
D) whole
Answer:
B) an irrational

Question 97.
Q ∪ Q’ = ………..
A) P
B) C
C) R
D) None
Answer:
A) P

Question 98.
……….. is called the additive identity.
A) 0
B) 1
C) 2
D) None
Answer:
B) 1

Question 99.
\(\sqrt{2}\) = 1.414 then 3 \(\sqrt{2}\) = ………..
A) 2.42
B) 13.42
C) 42.42
D) 4.242
Answer:
D) 4.242

Question 100.
\(\frac{23}{2^3 \cdot 5^2}\) = ……….
A) 11.5
B) 0.115
C) 1.15
D) 115.1
Answer:
A) 11.5

Question 101.
0.9375 = ……….
A) \(\frac{15}{16}\)
B) \(\frac{5}{16}\)
C) \(\frac{16}{15}\)
D) \(\frac{18}{1199}\)
Answer:
A) \(\frac{15}{16}\)

Question 102.
4\(\frac{1}{5}\) = ……….
A) 4.12
B) 4.2
C) 0.42
D) 4.02
Answer:
B) 4.2

Question 103.
\(\frac{5}{11}\) = ……….
A) \(0 . \overline{43}\)
B) \(0 . \overline{44}\)
C) \(0 . \overline{31}\)
D) \(0 . \overline{45}\)
Answer:
D) \(0 . \overline{45}\)

Question 104.
LCM of 12, 15 and 21 is ………
A) 420
B) 440
C) 820
D) 110
Answer:
A) 420

Question 105.
0.4 = ……..
A) \(\frac{2}{5}\)
B) \(\frac{5}{2}\)
C) \(\frac{1}{9}\)
D) None
Answer:
A) \(\frac{2}{5}\)

Question 106.
\(\sqrt{\frac{4}{9}}\) = …………
A) \(\frac{3}{2}\)
B) \(\frac{2}{3}\)
C) \(\frac{\sqrt{2}}{3}\)
D) \(\frac{2}{\sqrt{3}}\)
Answer:
B) \(\frac{2}{3}\)

Question 107.
HCF of 12, 18 is …………
A) 12
B) 9
C) 2
D) 6
Answer:
D) 6

Question 108.
2² × 5 × 7 = ………..
A) 240
B) 144
C) 140
D) 909
Answer:
C) 140

Question 109.
loga_a 1 ……. a > 0
A) a²
B) 2
C) 1
D) 0
Answer:
D) 0

Question 110.
log₂₀₁₅2015 = ………
A) 15
B) 1
C) 5
D) 0
Answer:
B) 1

Question 111.
Multiplicative inverse of 3\(\frac{1}{3}\) is ……..
A) 3\(\frac{1}{3}\)
B) \(\frac{3}{13}\)
c) \(\frac{3}{10}\)
d) \(\frac{3}{14}\)
Answer:
c) \(\frac{3}{10}\)

Question 112.
(ab)c = a(bc) is called …….. property.
A) Associative
B) Inverse
C) Identity
D) None
Answer:
A) Associative

Question 113.
\(\frac{41}{75}\) = ………..

Answer:

Question 114.
log 64 – log 4 = ………..
A) 4
B) 7
C) 1
D) None
Answer:
D) None

Question 115.
LCM of 306 and 657 is …….
A) 22338
B) 23238
C) 11128
D) None
Answer:
A) 22338

Question 116.
\(\frac{1167}{50}\) = ……….
A) 1.675
B) 23.34
C) 81.45
D) None
Answer:
B) 23.34

Question 117.
6ⁿ can not end with ………
A) 6
B) 0
C) 2
D) None
Answer:
B) 0

Question 118.
\(\sqrt{\mathbf{2 0 2 5}}\) = ………..
A) 405
B) 54
C) 45
D) 55
Answer:
C) 45

Question 119.
5⁵ = ……….
A) 1325
B) 1125
C) 3125
D) 1859
Answer:
C) 3125

Question 120.
\(\frac{3}{8}\) = ………
A) 0.375
B) 3.75
C) 8.175
D) None
Answer:
A) 0.375

Question 121.
\(\sqrt{5}\) = ……..
A) 1.414
B) 2.236
C) 1.73
D) 2.998
Answer:
B) 2.236

Question 122.
log₂16 = ………….
A) 2
B) 8
C) 4
D) 12
Answer:
C) 4

Question 123.
2 log 3 + 3 log 5 – 5 log 2 = ………
A) log \(\frac{1125}{32}\)
B) log \(\frac{125}{23}\)
C) log \(\frac{1025}{16}\)
D) None
Answer:
A) log \(\frac{1125}{32}\)

Question 124.
log₂ 1024 = ……….
A) 16
B) 20
C) 19
D) 10
Answer:
D) 10

Question 125.
log₁₈ 324 = ………
A) 2
B) 16
C) 19
D) 12
Answer:
A) 2

Question 126.
log₃ \(\frac{1}{27}\) = ………
A) 3
B) 6
C) -3
D) -7
Answer:
C) -3

Question 127.
log₆ 1 = ………….
A) 12
B) 19
C) 7
D) 0
Answer:
D) 0

Question 128.
128 + 32 = ……
A) 9
B) 6
C) 4
D) None
Answer:
C) 4

Question 129.
log₁₀ 10000 = ……
A) 4
B) 3
C) 2
D) None
Answer:
A) 4

Question 130.
log₂₇ 9 ……….
A) \(\frac{3}{2}\)
B) \(\frac{2}{3}\)
C) 1
D) A) \(\frac{1}{2}\)
Answer:
B) \(\frac{2}{3}\)

Question 131.
log₇ \(\sqrt{49}\) = ……..
A) 1
B) 10
C) 11
D) 12
Answer:
A) 1

Question 132.
Expanded form of log 1000 is
A) 3 log 2 + 3 log 5
B) 2 log 2 + log 5
C) log 2 – log 5
D) None
Answer:
A) 3 log 2 + 3 log 5

Question 133.
\(\frac{3}{2}\) (log x) – (log y) = ………….
A) log \(\frac{\sqrt{x^3}}{y^2}\)
B) log \(\sqrt{\frac{x^3}{y^2}}\)
C) log \(\frac{x^3}{y^2}\)
D) None
Answer:
B) log \(\sqrt{\frac{x^3}{y^2}}\)

Question 134.
\(\frac{13}{4}\) = ………….
A) 3.1251
B) 1.15
C) 3.25
D) None
Answer:
C) 3.25

Question 135.
(\(\sqrt{7}\) + \(\sqrt{5}\)) (\(\sqrt{7}\) – \(\sqrt{5}\)) = ……
A) 12
B) 10
C) 9
D) 2
Answer:
D) 2

Question 136.
2 \(\sqrt{3}\) + 7 \(\sqrt{3}\) + \(\sqrt{3}\)
A) 110 \(\sqrt{3}\)
B) 7 \(\sqrt{3}\)
C) 9 \(\sqrt{3}\)
D) 10 \(\sqrt{3}\)
Answer:
D) 10 \(\sqrt{3}\)

Question 137.
log₂ 512 = ……
A) 9
B) 10
C) 3
D) 12
Answer:
A) 9

Question 138.
Logarithmic form of a^x = b is ………..
A) log_b x = a
B) log_x b = a
C) log_b a = x
D) log_a b = x
Answer:
D) log_a b = x

Question 139.
10⁴ = ………
A) 10009
B) 10090
C) 10000
D) None
Answer:
C) 10000

Question 140.
……….. has no multiplication inverse.
A) \(\frac{9}{7}\)
B) \(\frac{2}{3}\)
C) \(\frac{9}{14}\)
D) 0
Answer:
D) 0

Question 141.
|-203| = ………….
A) 101
B) -203
C) 302
D) 203
Answer:
D) 203

Question 142.
log₃\(\frac{1}{9}\) = …….
A) 6
B) 4
C) 2
D) None
Answer:
D) None

Question 143.
HCF of 1 and 143 = …….
A) 1
B) 43
C) 34
D) 10
Answer:
A) 1

Question 144.
a(b + c) = ………
A) ab + c
B) bc + d
C) ab + ac
D) a + bc
Answer:
C) ab + ac

Question 145.
a + (-a) = 0 = (-a) + a is called ……. property.
A) Inverse
B) Identity
C) Commutative
D) None
Answer:
A) Inverse

Question 146.
log₃\(\frac{1}{9}\) = ……….
A) \(\frac{1}{4}\)
B) \(\frac{1}{2}\)
C) \(\frac{-5}{2}\)
D) \(\frac{-2}{5}\)
Answer:
D) \(\frac{-2}{5}\)

Question 147.
log₁₀100 = ………..
A) 2
B) 6
C) 0.1
D) None
Answer:
A) 2

Question 148.
\(\sqrt{12544}\) = ………
A) 161
B) 122
C) 112
D) 113
Answer:
C) 112

Question 149.
\(\sqrt{a}\) – \(\sqrt{b}\) = …………
A) ab
B) b\(\sqrt{a}\)
C) a\(\sqrt{b}\)
D) \(\sqrt{ab}\)
Answer:
D) \(\sqrt{ab}\)

Question 150.
Which of the following is a correct one
A) N ⊂ Z ⊂ W
B) N ⊂ W ⊂ Z
C) R ⊂ N ⊂ W
D) All the above
Answer:
B) N ⊂ W ⊂ Z

Question 151.
log_x \(\frac{\mathbf{a}}{\mathbf{b}}\) = …………..
A) log_x a – log_x b
B) log_x a + log_x b
C) logx ab
D) None
Answer:
A) log_x a – log_x b

These TS 10th Class Maths Chapter Wise Important Questions Chapter 1 Real Numbers given here will help you to solve different types of questions.

TS 10th Class Maths Important Questions Chapter 1 Real Numbers

Previous Exams Questions

Question 1.
Insert 4 rational numbers between \(\frac{3}{4}\) and 1 without using \(\frac{a+b}{2}\) formula. (T.S. Mar. ’15)
Solution:
\(\frac{3}{4}\) and 1 = \(\frac{3}{4}\) and \(\frac{4}{4}\)
\(\frac{3}{4}\) = \(\frac{30}{40}\) and \(\frac{4}{4}\) = \(\frac{40}{40}\)
So, in between \(\frac{30}{40}\) and \(\frac{40}{40}\) any 4 rational numbers to be noted.
\(\frac{30}{40}\), \(\frac{31}{40}\), \(\frac{32}{40}\), \(\frac{33}{40}\), \(\frac{34}{40}\) …………… , \(\frac{39}{40}\), \(\frac{40}{40}\)
So from \(\frac{31}{40}\) to \(\frac{39}{40}\) any four we can take.

Question 2.
Write any three numbers of two digits. Find the LCM and HCF for the above numbers by the Prime Factorization method. (T.S. Mar.’15)
Solution:
Take any three two digit numbers. Say 8, 10 and 12.
Prime factorization of these numbers are
8 = 2 × 2 × 2 = 2³
10 = 2 × 5 = 2 × 5
12 = 2 × 2 × 3 = 2² × 3
L.C.M of 8, 10 and 12 is 2 × 2² × 5 × 3 = 120
H.C.F of 8, 10 and 12 = 2

Question 3.
Give an example for each of the following :
i) The product of two irrational numbers is a rational number.
ii) The product of two irrational numbers is an irrational number. (T.S. Mar.’15)
Solution:
i) Let us consider two irrational numbers
\(\sqrt{2}\), \(\sqrt{50}\)
Their product is
= (\(\sqrt{2}\)) (\(\sqrt{50}\)) = \(\sqrt{100}\) = 10
which is a rational number.

ii) Again let us consider two irrational numbers = \(\sqrt{3}\), \(\sqrt{7}\)
Their product = (\(\sqrt{3}\)) (\(\sqrt{7}\)) = \(\sqrt{21}\)
which is an irrational number.

Question 4.
Find the value of \(\log _5^{125}\) (T.S. Mar.’16)
Solution:
We have the rule
if \(\log _a^N\) = x then a^x = N.
Let us consider \(\log _5^{125}\) = x
then 5^x = 125 = 5³
⇒ x = 3. So \(\log _5^{125}\) = 3.

Question 5.
If x² + y² = 7xy then show that 2 log (x + y) = log x + log y + 2 log 3. (T.S. Mar. ’15 )
Solution:
x² + y² = 7xy (given)
Add 2xy in both sides of above equation.
⇒ x² + y² + 2xy = 7xy + 2xy = 9xy
So (x + y)² = 9xy (Consider logarithm on both sides)
We get log (x + y)² = log 9xy
⇒ 21og (x + y) = log 9 + log x + log y
= log x + log y + log 3²
= log x + log y + 2 log 3
∴ 2 log (x + y) = log x + log y + 2 log 3
∴ Hence proved.

Question 6.
Use Eculid’s division lemma to show that the cube of any positive integer is of the form 7 m or 7m + 1 or 7m + 6.
Solution:
From the Euclid’s lemma we can consider a positive integer ‘a’
a = bq + r (r is the remainder)
Let us now consider a positive integer ‘a’ and
b = 7 then ‘a’ is in the form of
a = 7q + r
(r = either 0, 1,2, 3, 4, 5 or 6)
If r = 0 then a = 7q
r = 1 then a = 7q + 1
r = 2 then a = 7q + 2
r = 6 then q = 7q + 6
So ‘a’ will be in the form of anyone of the above
Then abc of the positive integer a is a³
So a = 7q + r
⇒ a² = (7q + r)²
(∵ (a + b)³ = a³ + b³ + 3a²b + 3ab²)
⇒ a³ = 343q³ + 49q²r + 7qr² + r³
= 7 [49q³ + 7q²r + qr²] + r³
= 7m + r³
[where 49q³ + 7q²r + qr² = m ]
a³ = 7m + r³
If r = 0 then a³ = 7m + 0³ = 7m
r = 1 then a³ = 7m + 1³ = 7m + 1
r = 2 then a³ = 7m + 2³
= 7m + 8
= 7 (m + 1) + 1
So it is m the form of 7m + 1
If r = 3 then a³ = 7m + 3³
= 7m + 27
= 7m + 21 + 6
= 7(m + 3) + 6
It is in the form of 7m + 6
If r = 4 then a³ = 7m + 4³
= 7m + 64
= 7m + 63 + 1
= 7(m + 9) + 1
= 7m + 1 form
if r = 5 then a³ = 7m + 5³
= 7m + 125
= 7m + 119 + 6
= 7(m + 17) + 6
= 7m + 6 form
If r = 6 then a³ = 7m + 6³
= 7m + 216
= 7m + 210 + 6
= 7(m + 30) + 6
= 7m + 6 form
So, cube of a positive integer will be either in the form of 7m, 7m, +1 or 7m + 6.

Question 7.
Show that \(\sqrt{2}\) – 3\(\sqrt{5}\) is a irrational number. (T.S. Mar. ’15)
Solution:
Consider \(\sqrt{2}\) – 3\(\sqrt{5}\) is not an irrational one. Then it will be a rational number. That means it will be in the form of \(\frac{\mathrm{p}}{\mathrm{q}}\) (q ≠ 0) (p, q are mutual prime)
∴ \(\sqrt{2}\) – 3\(\sqrt{5}\) = \(\frac{\mathrm{p}}{\mathrm{q}}\)
⇒ \(\sqrt{2}\) = \(\frac{\mathrm{p}}{\mathrm{q}}\) + 3\(\sqrt{5}\)
(squaring on both sides)

Since p and q are integers the RHS part of above equation (1) becomes a rational and RHS part \(\sqrt{5}\) is an irrational one which is unfair.
So our assumption is wrong.
Then \(\sqrt{2}\) – 3\(\sqrt{5}\) is an irrational number.

Additional Questions

Question 1.
Use Euclid’s division algorithm to find the HCF of
(i) 500 and 150
(ii) 194 and 35890
(iii) 1550 and 3150
Solution:
Theorem : Euclid’s Division Lemma a = bq + r, q > 0 and 0 < r < b
(i) 500 and 150
When 500 is divided by 150, then the remainder is 50 to get
500 = 150 × 3 + 50
Now consider division of 150 with the remainder 50 in the above and division algorithm to get
150 = 50 × 3 + 0
Then the remainder is zero. When we can not proceed further, we conclude that the
HCF of (500, 150) = 50

(ii) 194 and 35890
When 35890 is divided by 194, the remainder is zero to get
35890 = 194 × 185 + 0
The remainder is zero. When we can not proceed further, we conclude that the
HCF of (35890, 194) = 194

(iii) 1550 and 3150
When 1550 is divided by 3150 then the remainder is 50 to get
3150 = 1550 × 2 + 50
Now consider the division of 150 with the remainder 50 in the above and division algorithm to get
1550 = 50 × 31 + 0
The remainder is zero. When we can not proceed further we conclude that the
HCF of 3150, 1550 = 50

Question 2.
Use Euclid division Lemma to show that any positive even integer is of the form 4q or 4q + 2 or 4q + 4 when q is some integer.
Solution:
Let ‘a’ be any positive even integer. We apply the division algorithm with a and b = 4 since 0 ≤ r < 4, the possible remainder are 0, 1, 2, 3 and 4 (∵ a = bq + r)
i.e., a can be 4q or 4q + 1 or 4q + 2 or 4q + 3 or 4q + 4 where q is the quotient.
However since a is even, a cannot be 4q + 1 and 4q + 3 (∵ They are not divisible by 2)
∴ Any positive even integer in the form of 4q or 4q + 2 or 4q + 4.

Question 3.
Use Euclid division Lemma to show that any positive odd integer is of the form 2q + 1, 2q + 3 or 2q +5 when q is some integer.
Solution:
Let ‘a’ be any positive odd integer. We apply the division algorithm with a and b = 2
Since 0 ≤ r < 5, the possible remainders are
0, 1, 2, 3, 4 and 5 i.e., a can be 2q or 2q + 1 or 2q + 2 or 2q + 3 or 2q + 4 or 2q + 5 when q is the quotient.
However since ‘a’ is odd ‘a’ cannot be 2q or 2q + 2 or 2q + 4 (∵ They are divisible by 2)
Any odd integer is of the form 2q + 1 or 2q + 3 or 2q + 5

Question 4.
Use Euclid division Lemma to show that any positive even integer is of the form. 2q or 2q + 2 or 2q + 4 where q is some integer.
Solution:
Let a be and positive even integer. We apply the division algorithm with a and b = 2. Since 0 ≤ r < 4, the possible remainders are 0, 1,2, 3 and 4 (∵ a = bq + r)
1. e., a can be 2q or 2q + 1 or 2q + 2 or 2q + 3 or 2q + 4 where q is the quotient.
However, since a is even, a cannot be 2q + 1 and 2q + 3 (They are not divisible by 2)
∵ Any positive even integer is of the form 2q or 2q + 2 or 2q + 4

Question 5.
Express each number as a product of its prime factors.
(i) 540
(ii) 882
(iii) 1764
(iv) 1080
(v) 6292
Solution:
(i) 540 = 2 × 270
= 2 × 2 × 135
= 2² × 5 × 27
= 2² × 5 × 3 × 9
= 2² × 5 × 3 × 3²
= 2² × 5 × 3³

(ii) 882 = 2 × 441
= 2 × 3 × 147
= 2× 3 × 3 × 49
= 2 × 3² × 7 × 7
= 2 × 3² × 7²

iii) 1764 = 2 × 882
= 2 × 2 × 441
= 2² × 3 × 147
= 2² × 3 × 3 × 49
= 2² × 3² × 7²

iv) 1080 = 2 × 540
= 2 × 2 × 270
= 2² × 2 × 135
= 2³ × 5 × 27

v) 6292 = 2 × 3146
= 2 × 2 × 1573
= 2² × 11 × 143
= 2³ × 11 × 11 × 13
= 2² × 11² × 13

Question 6.
Find the LCM and HCF of the following integers by the prime factorisation method.
(i) 10, 15 and 35
(ii) 13, 17 and 23
(iii) 7, 9 and 25
(iv) 84 and 108
(v) 234 and 747
Solution:
HCF : Product of the smallest power of each common prime factors in the numbers.
LCM : Product of the greatest power of each prime factor in the numbers.

(i) 10, 15 and 35
10 = 5 × 2
15 = 5 × 3
35 = 5 × 7
HCF = 5,
LCM = 2 × 3 × 5 × 7
= 210

(ii) 13, 17 and 23
13 = 1 × 13
17 = 1 × 17
23 = 1 × 23
HCF = 1, LCM = 13 × 17 × 23 = 5083

(iii) 7, 9 and 25
7 = 1×7
9 = 1 × 3 × 3 = 1 × 3²
25 = 1 × 5 × 5 = 1 × 5²
HCF = 1, LCM = 7 × 3² × 5²
= 7 × 9 × 25 = 1575

(iv) 84 and 108
84 = 2 × 42 = 2 × 2 × 21 = 2² × 3 × 7
108 = 2 × 54 = 2 × 2 × 27 = 2² × 3³
HCF = 2² × 3 = 4 × 3 = 12
LCM = 2² × 3³ × 7 = 756

(v) 234 and 747
234 = 2 × 117 = 2 × 3 × 39 = 2 × 3 × 3 × 13
= 2 × 3² × 13
747 = 3 × 249
= 3 × 3 × 83
= 3² × 83
HCF = 3² = 9
LCM = 2 × 3² × 13 × 83 = 19422

Question 7.
Explain why 5 × 11 × 12 + 12 is a composite number.
Solution:
Note : Every composite number can be expressed as a product of primes.
Given numbers is 5 × 11 × 12 + 12
= 12(5 × 11 + 1)
= 12(55 + 1)
= 12 (56)
= 12 × 2 × 28
= 4 × 3 × 2 × 4 × 7
= 2² × 3 × 2 × 2² × 7
= 2⁵ × 3 × 7
= Product of prime factors Hence the given number is a composite number.

Question 8.
How will you show that 41 × 17 × 61 × 3 + 41 × 17 × 31 × 5 is a composite number ? Explain.
Solution:
Given number is 41 × 17 × 61 × 3 + 41 × 17 × 31 × 5
= 41 × 17 (61 × 3 + 31 × 5)
= 41 × 17(183 + 155)
= 41 × 17 (338)
= 41 × 17 × 2 × 169
= Product of prime factors
Since given number is a product of primes
∴ Given number is a composite number.

Question 9.
Expenses each member as a product of its prime factors.
(i) 504
(ii) 756
(iii) 1800
(iv) 8228
(v) 6084
Solution:
(i) 504
= 2 × 252
= 2 × 2 × 126
= 2² × 2 × 63
= 2³ × 9 × 7
= 2³ × 3² × 7

(ii) 756
= 2 × 378
= 2 × 2 × 189
= 2² × 3 × 63 ⇒ 2² × 3 × 3 × 21
= 2² × 3² × 3 × 7
= 2² × 3³ × 7

(iii) 1800
= 2 × 900
= 2 × 2 × 450
= 2² × 2 × 225
= 2³ × 3 × 75 ⇒ 2³ × 3 × 3 × 25
= 2³ × 3² × 5²

(iv) 8228
= 2 × 4114
= 2 × 2 × 2057
= 2² × 11 × 187
= 2² × 11 × 11 × 17
= 2² × 11² × 17

(v) 6084
= 2 × 3042
= 2 × 2 × 1521
= 2² × 3 × 507
= 2² × 3 × 3 × 169
= 2² × 3² × 13 × 13
= 2² × 3² × 132

Question 10.
Explain why 31 × 17 × 13 × 12 + 31 × 17 × 5 a composite number.
(Note : Every composite number can be expressed as a product of primes.
Solution:
Given number is 31 × 17 × 13 × 12 + 31 × 17 × 5
= 31 × 17(13 × 12 + 5)
= 31 × 17 (156 + 5)
= 31 × 17(161)
= 31 × 17 × 7 × 23
= Product of prime factors
Since given number is a product of primes.
∴ Given number is a composite number.

Question 11.
Write the following rational numbers in their decimal form and also state which are terminating and which have non-terminating, a repeating decimal.
(i) \(\frac{5}{8}\)
(ii) \(\frac{17}{200}\)
(iii) \(\frac{21}{125}\)
(iv) \(\frac{7}{11}\)
Solution:
(i) \(\frac{5}{8}\) = \(\frac{5}{2.2 .2}\) = \(\frac{5}{2^3}\) is a terminating decimal.
∵ Denominator consists of only 2’s
= \(\frac{5 \times 5^3}{2^3 \times 5^3}\) = \(\frac{5 \times 125}{10^3}\) = \(\frac{625}{1000}\)
= 0.625

(ii) \(\frac{17}{200}\) = \(\frac{17}{2.2 .2 .5 .5}\) = \(\frac{17}{2^3 \times 5^2}\) is a terminating decimal
∵ Denominator consists of only 2’s and 5’s

(iii) \(\frac{21}{125}\) = \(\frac{21}{5^3}\) is a terminating decimal
∵ Denominator consists of only 5’s

(iv) \(\frac{7}{11}\) is a non-terminating, repeating 2’s or 5’s or both
∵ Denominator doesn’t contain 2’s and 5’s or both ‘
\(\frac{7}{11}\) = 0.636363

Question 12.
Without actually performing division. State whether the following rational numbers will have a terminating decimal form or a non – terminating, repeating decimal form.
(i) \(\frac{14}{625}\)
(ii) \(\frac{13}{12}\)
(iii) \(\frac{74}{455}\)
(iv) \(\frac{76}{200}\)
Solution:
(i) \(\frac{14}{625}\) : It is the form of \(\frac{\mathrm{P}}{\mathrm{q}}\) .
\(\frac{14}{625}\) = \(\frac{14}{5.5 .5 .5}\) = \(\frac{14}{5^4}\)
∵ q = 5⁴ which is of the form 2ⁿ.5^m (n = 0, m = 4)
∴ Given rational number has a terminating decimal expansion.

(ii) \(\frac{13}{12}\) : It is of the form \(\frac{\mathrm{P}}{\mathrm{q}}\).
\(\frac{13}{12}\) = \(\frac{13}{2 \times 2 \times 3}\) = \(\frac{13}{2^2 \times 3}\) = 1 083333
∴ q = 2² × 3 which is not of the form 2ⁿ × 5^m
∴ Given rational number has a non-terminating repeating decimal expansion.

(iii) \(\frac{74}{455}\) : It is the form of \(\frac{\mathrm{P}}{\mathrm{q}}\).
\(\frac{74}{455}\) = \(\frac{74}{5 \times 7 \times 13}\)
∴ q = 5 × 7 × 13 which is not in the form 2ⁿ . 5^m
∴ Given rational number has a non terminating repeating decimal expansion.

(iv) \(\frac{76}{200}\) : It is of the form \(\frac{\mathrm{P}}{\mathrm{q}}\).
\(\frac{76}{200}\) = \(\frac{76}{2^3 \times 5^2}\)
∴ q = 2³ × 5² which is of the form 2ⁿ . 5^m (n = 3, m = 2)
∴ Given number has a terminating decimal expansion.

Question 13.
Write the decimal expansion of the following :
(i) \(\frac{27}{25}\)
(ii) \(\frac{35}{32}\)
(iii) \(\frac{43}{2^3 \cdot 5^2}\)
(iv) \(\frac{729}{3^2 \cdot 5^2}\)
Solution:
Hint: Convert the denominator into the form 10ⁿ or 2ⁿ.5^m.

Question 14.
Write the decimal expansion of the following.
(i) \(\frac{17}{25}\)
(ii) \(\frac{35}{16}\)
(iii) \(\frac{33}{2^3 \cdot 5^2}\)
(iv) \(\frac{243}{3^2 \cdot 5^2}\)
Solution:
Hint : Convert the denominator into the form 10ⁿ or 2ⁿ.5^m.

Question 15.
Prove the following are irrational.
(i) \(\sqrt{2}\) + \(\sqrt{5}\)
(ii) \(\sqrt{7}\)
(iii) 7 + \(\sqrt{3}\)
(iv) 6 – \(\sqrt{2}\)
Solution:
(i) \(\sqrt{2}\) + \(\sqrt{5}\)
Let us assume to the contrary that \(\sqrt{2}\) + \(\sqrt{5}\) is a rational number.
Then, there exist co-prime positive integers ‘a’ and ‘b’ such that

\(\frac{a^2-3 b^2}{2 a b}\) = \(\sqrt{2}\)
But \(\sqrt{2}\) is a rational number.
i.e., \(\frac{a^2-3 b^2}{2 a b}\) is rational.
This contracts the fact that \(\sqrt{2}\) is irrational.
So our assumption is wrong.
∴ Hence \(\sqrt{2}\) + \(\sqrt{5}\) is irrational.

(ii) \(\sqrt{7}\)
Let us assume, to the contrary, that \(\sqrt{5}\) is rational. Then there exist co-prime positive integer a and b such that
\(\sqrt{7}\) = \(\frac{a}{b}\)
\(\sqrt{7}\) b = a
SB.S., we get
7b² = a² …………….. (1)
7 divides a²
Hence 7 divides a
We can write a = 7c for same integer ‘c’. Substitute a = 7c in (1), we get
7b² = (7c)²
b² = \(\frac{49 c^2}{7}\) 7c²
7 divides b² and 7 divide b
‘a’ and ‘b’ have atleast as a common factor. This contradicts the fact that ‘a’ and ‘b’ have no common factor other than 1.
So our assumption is wrong.
∴ \(\sqrt{7}\) is irrational.

(iii) 7 + \(\sqrt{3}\)
Let us assume on the contrary that 7 + \(\sqrt{3}\) = is a rational. Then there exist co-prime positive integers ‘a’ and ‘b’ such that 7 + \(\sqrt{3}\) = \(\frac{a}{b}\)
\(\sqrt{3}\) = \(\frac{a}{b}\) – 7
⇒ \(\sqrt{3}\) = \(\frac{a-7 b}{b}\)
∴ \(\sqrt{3}\) is rational ⇒ \(\frac{a-7 b}{b}\) is rational.
This contradicts the fact that \(\sqrt{3}\) is irrational, so our assumption is wrong
∴ 7 + \(\sqrt{3}\) is irrational.

(iv) 6 – \(\sqrt{2}\)
Let us assume on the contrary that 6 – \(\sqrt{2}\) is rational. Then there exist co-prime positive in-tegers ‘a’ and ‘b’ such that
6 – \(\sqrt{2}\) = \(\frac{a}{b}\)
⇒ 6 – \(\frac{a}{b}\) = \(\sqrt{2}\)
⇒ \(\frac{6 b-a}{b}\) = \(\sqrt{2}\)
\(\sqrt{2}\) is rational \(\frac{6 b-a}{b}\) is rational. This contradicts the fact that \(\sqrt{2}\) is irrational. So our assumption is wrong.
∴ 6 – \(\sqrt{2}\) is irrational.

Question 16.
Prove that \(\sqrt{\mathrm{p}}\) – \(\sqrt{\mathrm{q}}\) is irrational when p, q are primes.
Solution:
Let us assume to the contrary that \(\sqrt{\mathrm{p}}\) – \(\sqrt{\mathrm{q}}\) is rational. Then exist co-prime positive integers ‘a’ and ‘b’

We know that square root of any prime number in irrational. We get \(\sqrt{\mathrm{q}}\) is a rational.
This contradicts the fact that \(\sqrt{\mathrm{q}}\) is irrational. So, our assumption is wrong.
∴ \(\sqrt{\mathrm{q}}\) is irrational
∴ Hence \(\sqrt{\mathrm{p}}\) – \(\sqrt{\mathrm{q}}\) is irrational.

Question 17.
Prove that the following are irrational
(i) \(\sqrt{5}\) + \(\sqrt{3}\)
(ii) \(\sqrt{3}\)
(iii) 7 + \(\sqrt{2}\)
Solution:
(i) \(\sqrt{5}\) + \(\sqrt{3}\)
Let us assume to the contrary that \(\sqrt{5}\) + \(\sqrt{3}\) is a rational number.
Then exist co-prime positive integers ‘a’ and ‘b’ such that
\(\sqrt{5}\) + \(\sqrt{3}\) = \(\frac{a}{b}\)

This contradicts the fact that \(\sqrt{3}\) is irrational. So our assumption is wrong.
∴ Hence \(\sqrt{5}\) + \(\sqrt{3}\) is irrational.

(ii) \(\sqrt{3}\)
Let us assume to the contrary, that \(\sqrt{3}\) is rational. Then there exist co-prime positive integers a and b such that
\(\sqrt{3}\) = \(\frac{a}{b}\)
\(\sqrt{3}\)b = a
S.B.S. We get
3b² = a² ………………. (1)
3 divides a²
We can write a = 3c for same integer c substitute a = 3c in (1), we get
3b² = (3c)²
b² = \(\frac{9 c^2}{3}\) = 3c²
3 divides b² and 3 divide b.
‘a’ and ‘b’ have atleast as a common factor. This contradicts the fact that ‘a’ and ‘b’ have no common factor other than 1.
So, our assumption is wrong.
∴ \(\sqrt{3}\) is irrational.

(iii) 7 + \(\sqrt{2}\)
Let us assume on the contrary that 7 + \(\sqrt{2}\) is a rational. Then there exist co-prime positive integers ‘a’ and ‘b’ such that
7 + \(\sqrt{2}\) = \(\frac{a}{b}\)
\(\sqrt{2}\) = \(\frac{a}{b}\) – 7
\(\sqrt{2}\) = \(\frac{a-7 b}{b}\)
\(\sqrt{2}\) is rational ⇒ \(\frac{a-7 b}{b}\) is rational.
This contradicts the fact that \(\sqrt{2}\) is irrational. So our assumption is wrong.
∴ 7 + \(\sqrt{2}\) is irrational

Question 18.
Determine the value of the following.

Solution:

Question 19.
Write each of the following expressions! as log N. Determine the value of N. (Take the base as 10).
(i) log 2 + log 50
(ii) log 50 – log 2
(iii) 4 log 3
(iv) 3 log 2 – 2 log 3
(v) log 343 + log 1
(vi) 3 log 2 + 2 log 5 – 4 log 2
Solution:
(i) log 2 + log 50
∵ log x + log y = log xy
log 2 + log 50 = log (2 × 50)
= log 100
= \(\log _{10}^{10^2}\) = 2 . \(\log _{10}^{10}\)
= 2 × 1 = 2
∵ log a^m = m log a and \(\log _a^a\) = 1

(ii) log 50 – log 2
∵ log x – log y = log \(\left(\frac{x}{y}\right)\)
log 50 – log 2 = log\(\left(\frac{50}{2}\right)\) = log 25

(iii) 4 log 3
(∵ m log a = log a^m)
4 log 3 = log 3⁴ = log 81

(iv) 3 log 2 – 2 log 3
3 log 2 – 2 log 3 (∵ m log a = log a^m)
⇒ log 2³ – log 3²
∵ log x – log y = log \(\left(\frac{x}{y}\right)\)
= log 8 – log 9 = log \(\left(\frac{8}{9}\right)\)

(v) log 343 + log 1
log 343 + log 1
∵ log x + log y = log (xy)
= log (343 × 1) = log 343

(vi) 3 log 2 + 2 log 5 – 4 log 2
3 log 2 + 2 log 5 – 4 log 2
∵ m log a = log a^m
= log 2³ + log 5² – log 2⁴
= log 8 + log 25 – log 16
= log \(\left(\frac{8 \times 25}{16}\right)\) = log \(\left(\frac{25}{2}\right)\)

Question 20.
Evaluate each of the following in terms of x and y, if it is given x = \(\log _2^3\) and \(\log _2^5\).
(i) \(\log _2^75\)
(ii) \(\log _2^4.5\)
(iii) \(\log _2^90\)
Solution:

Question 21.
Expand the following.
(i) Log 10000
(ii) log \(\left(\frac{243}{625}\right)\)
(iii) log (x³y²z⁵)
(iv) log \(\left(\frac{p^3 \mathrm{q}^4}{r}\right)\)
(v) log \(\sqrt{\frac{x^5}{y^3}}\)
Solution:
(i) Log 10000
log (10000) = log (2⁴ × 5⁴)
∵ log(xy) = log x + log y
∵ log a^m = m log a
= log2⁴ + log5⁴
= 4 log 2 + 4 log 5
= 4(log 2 + log 5)

(ii) \(\left(\frac{243}{625}\right)\)
log 243 – log 625
= log3⁵ – log5⁴
= 5 log3 – 4 log5

(iii) log (x³y²z⁵)
= log (x³y²z⁵)
= log x³ + log y² + log z⁵
= 3 log x + 2 log y + 5 log z

(iv) log \(\left(\frac{p^3 \mathrm{q}^4}{r}\right)\)
log \(\left(\frac{p^3 \mathrm{q}^4}{r}\right)\) = log p³ + log q⁴ – log r
log p³ + log q⁴ – log r
= 3 log p + 4 log q – log r

(v) log \(\sqrt{\frac{x^5}{y^3}}\)
log \(\sqrt{\frac{x^5}{y^3}}\) = log \(\left(\frac{x^5}{y^3}\right)^{\frac{1}{2}}\)
= \(\frac{1}{2}\) log \(\left(\frac{x^5}{y^3}\right)\)
= \(\frac{1}{2}\) [log(x⁵) – log(y³)]
= \(\frac{1}{2}\) [5 log x – 3 log y]

Question 22.
Determine the value of the following

Solution:
(i) \(\log _{64}^4\)
Let \(\log _{64}^4\) = x
∵ \(\log _a^N\) = x
⇒ N = a^x
4 = (64)^x
4 = (4³)^x ⇒ 4 = 4^3x
⇒ 4^3x = 4¹ ⇒ 3x = 1 ⇒ x = \(\frac{1}{3}\)

(ii) \(\log _{216}^6\)
Let \(\log _{216}^6\) = x
∵ \(\log _a^N\) = x
⇒ N = a^x
6 = (216)^x
⇒ (216)^x = 6 ⇒ (6³)^x = 6¹
⇒ 6^3x = 6¹ ⇒ 3x = 1 ⇒ x = \(\frac{1}{3}\)

(vii) \(\log _{10}^{0.0001}\)
Let \(\log _{10}^{0.0001}\) = x
0.0001 = 10^x ⇒ 10^x = 0.0001
= \(\frac{1}{10000}\) = \(\frac{1}{10^4}\)
10^x = 10^-4 ⇒ x = -4

(viii) \(3^{2+\log _3^7}\)
= \(3^{2+\log _3^7}\)
∵ a^{m + n} = a^m × aⁿ
= 3ⁿ × 3 \(\log _3^7\) (∵\(a^{\log _a^m}\) = m)
= 9 × 7 = 63

Question 23.
Write each of the following expressions as below. Determine the value of N. (Take the base as 10)
(i) log 4 + log 25
(ii) log 100 – log 2
(iii) 3 log 5
(iv) 2 log 4 – 3 log 2
(v) log 625 + log 1
(vi) 2 log 3 + 3 log 4 – 2 log 5
Solution:
(i) log 4 + log 25
log 4 + log 25 (∵ log x + log y = log xy)
= log (4 × 25)
= log 100 = \(\log _{10}^{10^2}\) = 2.\(\log _{10}^{10}\) = 2 × 1 = 2
(∵ log a^m = m log a and \(\log _{a}^{a}\) = 1)

(ii) log 100 – log 2
log 100 – log 2 (∵ log x – log y = log \(\left(\frac{x}{y}\right)\))
= log \(\left(\frac{100}{2}\right)\) = log 50

(iii) 3 log 5
(∵ m log x = log a^m)
3 log 5 = log 5³ = log 125

(iv) 2 log 4 – 3 log 2
(∵ m log a = log a^m)
2 log 4 – 3 log 2 = log 4² – log 2³
= log 16 – log 8
(∵ log x – log y = log \(\left(\frac{x}{y}\right)\))
= log latex]\left(\frac{16}{8}\right)[/latex] = log 2

(v) log 625 + log 1
(∵ log x + log y = log xy)
= log (625 × 1)
= log 625

(vi) 2 log 3 + 3 log 4 – 2 log 5
(∵ m log a = log a^m)
= log 3² + log 4³ – log 5²
= log 9 + log 64 – log 25
= log \(\left(\frac{9 \times 64}{25}\right)\) = log \(\left(\frac{576}{25}\right)\)

Question 24.
Find the value of Log₁₀ 0.001
Solution:
Let Log₁₀ 0.001 = x
10^x = o.001 = \(\frac{1}{1000}\)
10^x = \(\frac{1}{10^3}\) = 10^-3
10^x = 10^-3 ⇒ x = -3

Question 25.
Find the LCM and HCF of the following integers by the prime factorization method. 72 and 108
Solution:
72 and 108
72 = 2 × 36 = 2 × 2 × 18 = 2² × 2 × 9
= 2³ × 3²
108 = 2 × 54 = 2 × 2 × 27 = 2² × 2³
L.C.M = 2³ × 2³ = 8 × 27 = 216
H.C.F. = 2² × 3² = 4 × 9 = 36

Question 26.
Write 2log3 + 3log5 – 5log 2 as single logarithm.
Solution:
2log 3 + 3log 5 – 5log 2 (∵ mloga = loga^m)
= log 3² + log 5³ log 2⁵
= log 9 + log 125 – log 32 [∵ log x + log y = log(xy)]
= log \(\left(\frac{9 \quad 125}{32}\right)\) = log \(\left(\frac{1125}{32}\right)\)
(∵ log x – log y = log \(\left(\frac{x}{y}\right)\))

Question 27.
Prove that the \(\frac{1}{\sqrt{3}}\) is irrational.
Solution:
Let us consider \(\frac{1}{\sqrt{3}}\) is a rational number.
Then take \(\frac{1}{\sqrt{3}}\) = \(\frac{\mathrm{p}}{\mathrm{q}}\) form (where p, q are integers)
⇒ \(\frac{\mathrm{p}}{\mathrm{q}}\) = \(\sqrt{3}\)
i.e. \(\sqrt{3}\) is a rational number and it is a \(\frac{1}{\sqrt{3}}\) contradiction Hence is an irrational number.

Question 28.
Prove that the 3 + 2\(\sqrt{5}\) is irrational
Solution:
Let us assume that 3 + 2\(\sqrt{5}\) is a rational number
3 + 2\(\sqrt{5}\) = \(\frac{\mathrm{p}}{\mathrm{q}}\) (q ≠ 0)
2\(\sqrt{5}\) = \(\frac{\mathrm{p}}{\mathrm{q}}\) – 3 = \(\frac{\mathrm{p – 3q}}{\mathrm{q}}\)
\(\sqrt{5}\) = \(\frac{p-3 q}{2 q}\)
Here p, q being intergers we can say that \(\frac{p-3 q}{2 q}\) is a rational number.
This contradicts that fact that \(\sqrt{5}\) is an irrational number.
Hence our assumption is wrong.
∴ 3 + 2\(\sqrt{5}\) is an irrational number.

Question 29.
Determine the value of

Solution:

∵ \(\log _a^N\) = x
⇒ N = a^x
⇒ \(\left(\frac{3}{5}\right)^x\) = \(\frac{243}{3125}\) = \(\left(\frac{3}{5}\right)^x\)
∵ Bases are equal
∵Powers are equal
x = 5

Question 30.
Solve 7^x = 9^x-2
Solution:
Given 7^x = 9^x-2
Taking log an both sides
log 7^x = log 9^x-2
⇒ x log 7 = (x – 2) log 9
x log 7 = x log 9 – 2 log 9
⇒ 2 log 9 = x log 9 – x log 7
2 log 9 = x (log 9 – log 7)
∴ x = \(\frac{2 \log 9}{\log 9-\log 7}\)

Question 31.
Establish the relation among the sets of Real Numbers, Rational, Irrational, Integers, whole numbers and Natural Numbers using Venn diagrams.
Solution:

N = the set of natural number
W = the set of whole number
Z = the set of integers
Q = the set of rational number
S = the set of irrational number
R = the set of real number

Question 32.
Prove that 2\(\sqrt{5}\) + \(\sqrt{7}\) is an Irrational Number. Also check whether (2\(\sqrt{5}\) + \(\sqrt{7}\)) (2\(\sqrt{5}\) – \(\sqrt{7}\)) is rational or Irrational.
Solution:
Let us consider 2\(\sqrt{5}\) + \(\sqrt{7}\) be a rational number.
Then 2\(\sqrt{5}\) + \(\sqrt{7}\) = \(\frac{p}{q}\)
Squaring on both sides, we get

LHS is an irrational number.
RHS = p, q being integers, \(\frac{p^2-69 q^2}{4 q^2}\) is a rational number.
This is a contradiction to the fact that \(\sqrt{35}\) is an irrational. Hence our assumption is wrong, and 2 \(\sqrt{5}\) + \(\sqrt{7}\) is an irrational number.
Also
(2\(\sqrt{5}\) + \(\sqrt{7}\)) (2\(\sqrt{5}\) – \(\sqrt{7}\)) = (2\(\sqrt{5}\))² – (\(\sqrt{5}\))²
= 20 – 7
= 13, a rational number

Telangana SCERT 10th Class Physics Study Material Telangana 1st Lesson Reflection of Light at Curved Surfaces Textbook Questions and Answers.

TS 10th Class Physical Science 1st Lesson Questions and Answers Reflection of Light at Curved Surfaces

Improve Your Learning
I. Reflections on concepts

Question 1.
Where will the image be formed when we place an object, on the principal axis of a concave mirror at a point between focus and centre of curvature?
Answer:
1. When we place an object on the principal axis of concave mirror at a point between focus and centre of curvature, the image is formed beyond centre of curvature.

2. The image so formed is real, inverted and magnified.

Question 2.
State the differences between convex and concave mirrors.
Answer:

Question 3.
Distinguish between real and virtual images.
Answer:

Question 4.
How do you get a virtual image using a concave mirror?
Answer:
A. When an object is kept between pole and focus of a concave mirror virtual image is formed behind the mirror.

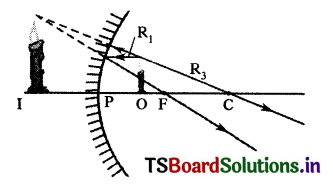
Question 5.
What do you know about the terms given below related to spherical mirrors?
(a) pole
(b) centre of curvature
(c) focus
(d) Radius of curvature
(e) Focal length
(f) principal axis
(g) object distance
(h) image distance
(i) Magnification.
Answer:
(a) Pole: The point on the principal axis of spherical mirror with respect to which all the measurements are made. Usually, it is the mid point of the curvature of mirror.

(b) Centre of curvature: The centre of the sphere of which the curved surface of the mirror is a part.

(c) Focus: The light rays coming from a source parallel to the principal axis converge at a point after reflection. This point is called focus or focal point.

(d) Radius of curvature: The radius of the sphere of which the curved surface is a part is called radius of curvature.

(e) Focal length: The distance between the pole of the mirror and focus is called focal length of mirror.

(f) Principal axis: The straight line passing through the centre of curvature and pole of curved mirror is called principal axis.

(g) Object distance: The distance between the pole of the mirror and object position of object is known as object distance.

(h) Image distance: The distance between the pole of the mirror and position of image is called image distance.

(i) Magnification: Magnification of a spherical mirror is the ratio between size (height) of image to the size (height) of object. Also, m= v/u.

Question 6.
What do you infer from the experiment which you did to measure the object distance and image distance?
Answer:
Inference from the experiment which I did with concave mirror :

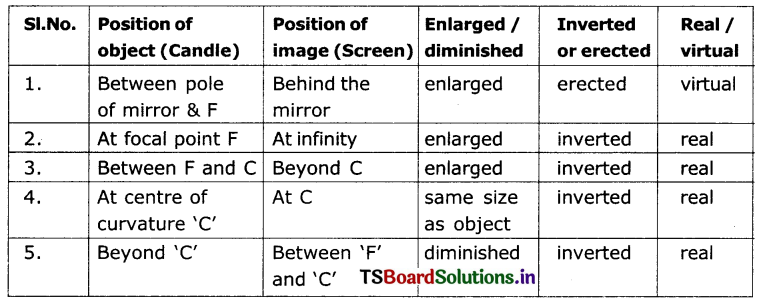
Inference:

1. As the object moves away from the mirror the image approaches the mirror.
2. As the object moves away from mirror the size of the image becomes smaller.

Question 7.
Write the rules for sign convention.
Answer:
Rules for sign convension:

1. AN distances should be measured from the pole.
2. The distances measured in the direction of incident light, are taken positive and the opposite direction of incident light are taken negative.
3. Height of object (H₀) and height of image (H₁) are positive if measured upward
   from the axis and negative if measured downward.
4. For a concave mirror ‘f’ and ‘R’ are negative and for a convex mirror these are positive.

II. Application of concepts

Question 1.
Find the distance of the image, when an object is placed on the principal axis, at a distance of 10 cm in front of a concave mirror whose radius of curvature is 8 cm.
Answer:
Object distance u = -10 cm
Radius of curvature (r) = -8cm
Image distance v=?

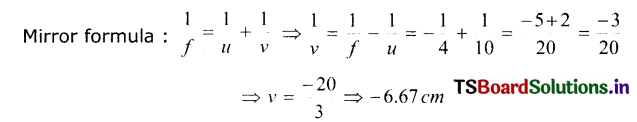
The image distance (v) = 6.7 cm.
i.e., Real image is formed at same side of the mirror.

Question 2.
The magnification product by a plane mirror is +1. What does it mean?
Answer:

1. Magnification = \(\frac{\text { height of the image }}{\text { height of the object }}=\frac{\text { distance of the image }}{\text { distance of the object }}\)
2. The magnification produced by a plane mirror is +1 means then the size of the image is equal to the size of the object.
3. + sign indicates that the image is erect. Magnification ‘+1’ indicates the image is erect and size of the image is equal to size of the object.

Question 3.
If the spherical mirrors were not known to human beings, guess the consequences.
Answer:
If spherical mirrors are not known to human beings

1. Many optical instruments would not have been invented.
2. We cannot increase the size of images of the objects.
3. The problem of lateral inversion of images will not be solved.
4. Now a days spherical mirrors are used as shaving mirrors, head mirrors for ENT specialists, in headlights of motor vehicles, in solar furnaces and as rearview mirror. If spherical mirrors are not known all these are not possible.

Question 4.
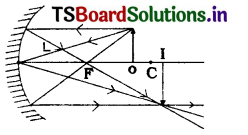
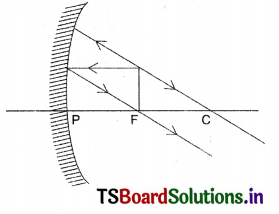
Draw suitable rays by which we can guess the position of the imge formed by a concave mirror.
Answer:
The following rays are used to guess the position of the image formed by a concave mirror.
(i) A ray parallel to the principal axis passes through principal focus (F) after reflection from a concave mirror.

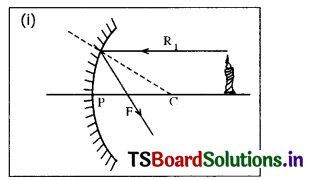
(ii) A ray passing through ‘F’ becomes parallel to principal axis after reflection from a concave mirror.

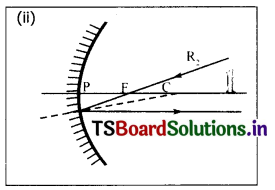
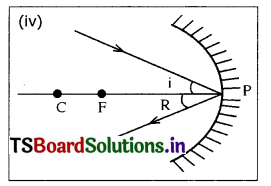
(iii) A ray passing through ‘C’ is reflected back along the same path after reflection from a concave mirror.

(iv) A ray incident obliquely to the principal axis towards the pole P, on the concave mirror is reflected obliquely, following the laws of reflection.

Question 5.
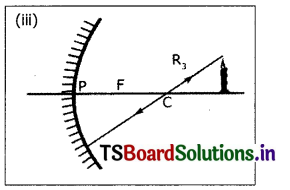
Show the formation of image with a ray diagram, when an object is placed on the principal axis of a concave mirror away from the centre of curvature.
Answer:
When an object is placed on the principal axis of a concave mirror and beyond (away from) its centre of curvature ‘C’, the image is formed between the focus (F) and the centre of curvature (C). The ray which is parallel to principle axis will pass through focus after reflection and the ray which passes through focus will travels parallel to principal axis after reflection. These two rays will converge between F and C of the mirror.

The image is real, inverted and diminished in size.

Question 6.
Why do we prefer a convex mirror as a rear-view mirror in the vehicles?
Answer:
We use convex mirror as a rear-view mirror in the vehicles because

1. Convex mirror always forms virtual, erect, and diminished images irrespective of distance of the object.
2. A convex mirror enables a driver to view large area of the traffic behind him.
3. Convex mirror forms very small image than the object. Due to this reason convex mirrors are used as rear-view mirrors in vehicles.

III. Higher Order Thinking Questions

Question 1.
A convex mirror with a radius of curvature of 3 m is used as a rearview mirror for a vehicle. If a bus is located at 5m from this mirror, find the position, nature, and size of the image.
Answer:
According to the sign convention :
Radius of curvature = R = + 3m
Object distance = u = -5 m (negative sign)
Image distance = v =?
Focal length, f = \(\frac{R}{2}=\frac{3}{2} m\) = 1.5 m
Formula : \(\frac{1}{f}=\frac{1}{u}+\frac{1}{v}\)

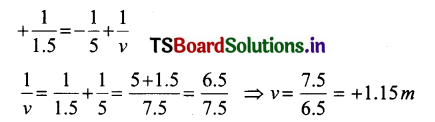
The image is formed at a distance of 1.15 m at the back of the mirror.
Magnification, m = \(\frac{h_i}{h_o}=-\frac{v}{u}=\frac{-1.15 m}{-5 m}=\frac{1.15}{5}\) = 0.23
The image is virtual, erect, and diminished to 0.23 times of the size of the object.

Question 2.
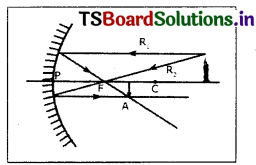
To form the image on the object itself, how should we place the object in front of a concave mirror? Explain with a ray diagram.
Answer:
To form the image on the object itself, the object should be kept at center of curvature of a concave mirror.

1. An object AB has been placed at the centre of curvature ‘C’ on the concave mirror.
2. A ray of light AD which is parallel to principle axis passes through the focus ‘F after reflection as DA’.
   
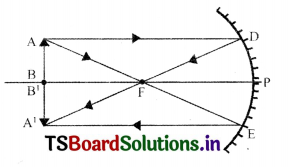
3. A ray of light passing through the focus of the concave mirror becomes parallel to the principle axis after reflection.
4. Here AE ray passing through focus and reflected as EA’.
5. The reflected rays DA’ and EA’ meet at A’ point. So the real image formed at point A’ of the object.
   We get couple image AB perpendicular to the principal axis.
6. Thus A’B’ is the real inverted image of the object AB.

IV. Multiple choices questions

Question 1.
If an object is placed at ‘C’ on the principal axis in front of a concave mirror, the position of the image is ………………. . [ ]
(a) at infinity
(b) between F and C
(c) at C
(d) beyond C
Answer:
(c) at C

Question 2.
We get a diminished image with a concave mirror when the object is placed ………………………. . [ ]
(a) at F
(b) between the pole and F
(c) at C
(d) beyond C
Answer:
(d) beyond C

Question 3.
We get a virtual image in a concave mirror when the object is placed …………………….. . [ ]
(a) at F
(b) between the pole and F
(c) at C
(d) beyond C
Answer:
(b) between the pole and F

Question 4.
Which of the following represents Magnification? [ ]
(i) \(\frac{v}{u}\)
(ii) \(\frac{-v}{u}\)
(iii) \(\frac{h_i}{h_0}\)
(iv) \(\frac{h_0}{h_i}\)
(a) i, ii
(b) ii, iii
(c) iii, iv
(d) iv, i
Answer:
(d) iv, i

Question 5.
ray which seems to be traveling through the focus of a convex mirror, path of the reflected ray of an incident ……………… . [ ]
(a) parallel to the axis
(b) along the same path in opposite direction
(c) through F
(d) through C
Answer:
(a) parallel to the axis

Question 6.
Size of image formed by a convex mirror is always …………………… .[ ]
(a) enlarged
(b) diminished
(c) equal to the size of object
(d) depends on position of object
Answer:
(b) diminished

Question 7.
An object is placed at a certain distance on the principal axis of a concave mirror. The image is formed at a distance of 30 cm from the mirror. Find the object distance if radius of curvature R = 15cm. [ ]
(a) 15 cm
(b) 10 cm
(c) 30 cm
(d) 7.5 cm
Answer:
(c) 30 cm

Question 8.
All the distances related to spherical mirror will be measured from …………………… .[ ]
(a) object to image
(b) focus of the mirror
(c) pole of the mirror
(d) image to object
Answer:
(c) pole of the mirror

Question 9.
The minimum distance from real object to a real image in a concave mirror is ………………….. . [ ]
(a) 2f
(b) f
(c) 0
(d) f/2
Answer:
(c) 0

Suggested Experiments

Question 1.
Conduct an experiment to find the focal length of concave mirror.
(or)
How can you find out the focal length of concave mirror experimentally when there is no sunlight?
Answer:
Aim: To find the focal length of a concave mirror,
Materials required : (i) A concave mirror (ii) V-shape stand (iii) A candle (iv) A meter scale.

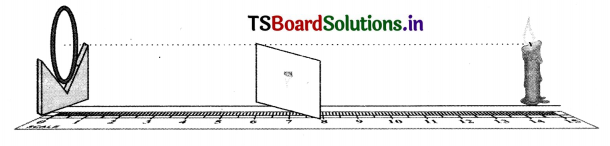
Procedure :

1. Place the concave mirror on the V-shape stand.
2. Keep a burning candle in front of the concave mirror.
3. Place a thick white paper behind the candle. This acts as a screen.
4. Adjust distances between candle and mirror, screen and mirror by moving them either forward or backward till a clear well-defined image appears on the screen.
5. Measure the distance between the mirror and candle (object distance u) and the distance between mirror and screen (image distance v).
6. Using the mirror formula, \(\frac{1}{f}=\frac{1}{u}+\frac{1}{v} \) or f = \(\frac{u v}{u+v} \)
   This gives the focal length of the concave mirror.

Question 2.
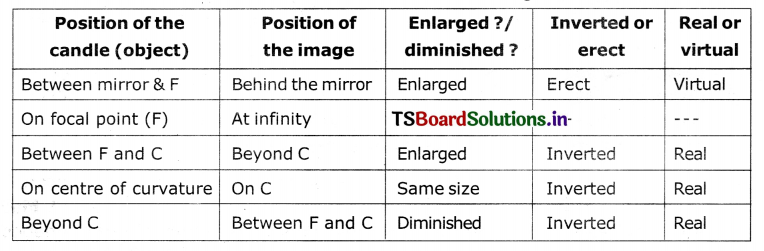
Find the nature and position of images when an object is placed at different places on the principal axis of a concave mirror.
Answer:
Aim: Observing the types of images and measuring the object distance and image distance from the concave mirror.
Material required: A candle, paper, concave mirror (known focal length), V- stand, measuring tape or meter scale.

Procedure:

1. Place the concave mirror on V-stand, a candle and meter scale as shown in figure.
   
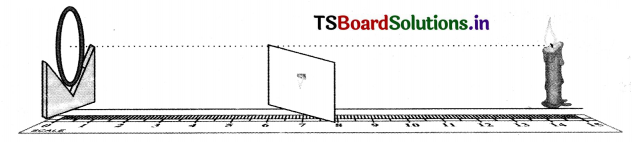
2. Keep the candle at different distances from the mirror (10 cm to 80 cm) along the axis and by moving the paper screen find the position where you get the sharp image on paper.
3. Note down your observations in the following table.
4. Since we know the focal point and centre of curvature, we can classify our above observations as shown in the following table.

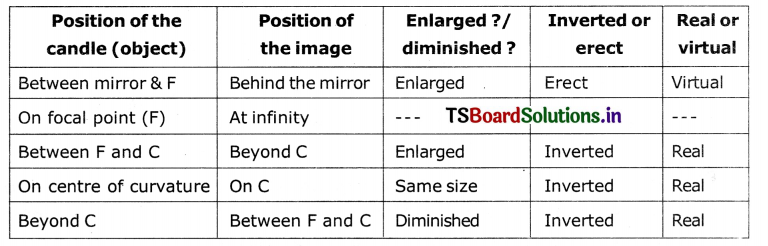
Suggested Project Works

Question 1.
Collect information about the history of spherical mirrors in human civilization, write a report on it.
Answer:

1. The first mirrors used by people were most likely pools of water or still water. The earliest manufactured mirrors were pieces of polished stones.
2. Parabolic mirrors were described and studied in classical antiquity by the mathematician Archimedes in his work on burning mirrors.
3. Ptolemy conducted a number of experiments with curved polished iron mirrors. He also discussed plane, convex, concave, and spherical mirrors in his optics.
4. In China, people began making mirrors with the use of silver mercury amalgams as early as 500 AD.
5. In 16th century, Venice, a big city popular for its glass-making expertise, became a centre of mirror production using this new technique.
6. The invention of the silvered-glass mirror is credited to German Chemist Justus Von Liebig in 1835.

Question 2.
Think about the objects which act as concave or convex mirrors in your surroundings. Make a table of these objects and display in your classroom.
Answer:

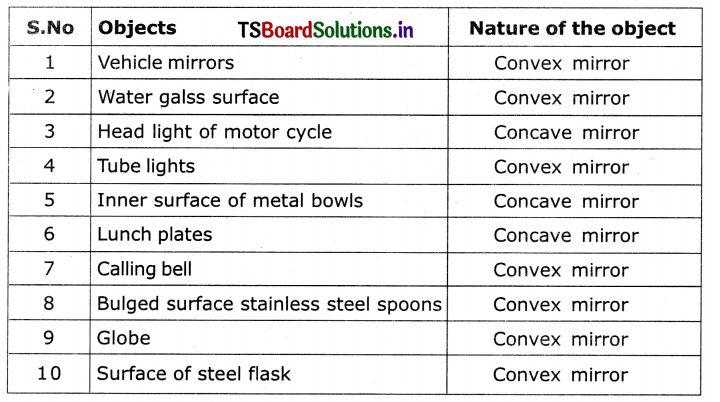
Question 3.
Collect photographs from your daily life where you use convex and concave mirrors and display in your classroom.
Answer:

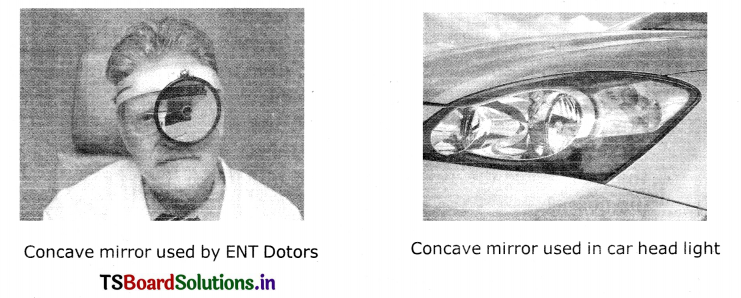
TS 10th Class Physical Science Reflection of Light at Curved Surfaces Intext Questions

Page 1

Question 1.
Is the image formed by a bulged surface same as the image formed by a plane mirror?
Answer:
No, the image formed by a bulged surface is virtual, created, and diminished image.

Question 2.
Is the mirror used in automobiles a plane mirror? Why it is showing small images?
Answer:
No, the mirror used in automobile is convex mirror. At it bulging outwards it forms small images.

Question 3.
Why does our image appear thin or bulged out in some mirrors?
Answer:
The image in a mirror appears thin or bulged out because the thickness of the mirror may vary or the reflecting surface may not be flat.

Question 4.
Can be see inverted image in any mirror?
Answer:
Can we see inverted image in any mirror? Yes, we can see inverted image in concave mirror for a distant objects.

Question 5.
Can we focus the sunlight at a point using a mirror instead of a magnifying glass?
Answer:
Yes. By using a black paper with a tiny hole at its centre.

Question 6.
Are the angle of reflection and angle of incidence also equal for reflection by curved surfaces?
Answer:
No.

Page 4

Question 7.
Does this help you to verify the conclusions you arrived at with your drawing?
Answer:
Yes.

Question 8.
What happens if you hold the paper at a distance shorter than the focal length from the mirror and move it away?
Answer:
We find there is no point at which the reflected rays converge at a point. But as we move the paper away from the focal point, we find images formed at different distances from the mirror.

Question 9.
Does the image of the sun become smaller or bigger?
Answer:
We notice that the image of the sun keeps on becoming smaller. Beyond the focal point, it will become bigger.

Page 5

Question 10.
Do we get an image with a concave mirror at the focus every time?
Answer:
We get the images not only at the focus every time, we get different ¡mages by keeping the object at different points depending on focal length of mirror.

Page 6

Question 11.
It is inverted or erect, enlarged or diminished?
Answer:

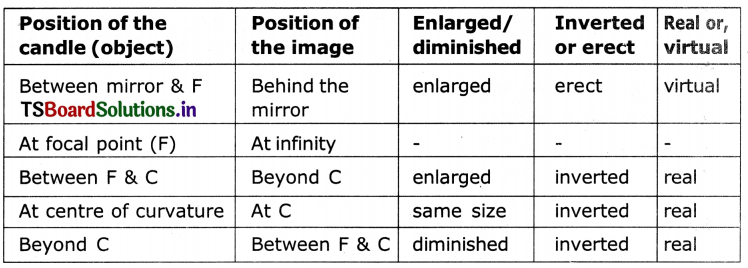
Question 12.
What do you infer from the table?
Answer:
From the table 2. I infer that images can be formed at other positions different from focal point.

Page 7

Question 13.
Why only at point A?
Answer:
If we hold the screen at any point before or beyond point A (for example at point B), we see that the rays will meet the screen at different points due to these rays. If we draw more rays emanating from the same tip we will see that
at point A they will meet but at point B they do not. So the image of the tip of the flame will be sharp at point A.

Page 9

Question 14.
Where is the base of the candle expected to be in the image when the candle is placed on the axis of the mirror?
Answer:
The base of the candle is going to be on the principle axis ¡n the image when the object is placed on the axis of the mirror.

Question 15.
During the experiment, did you get any positions where you could not get an image on the screen?
Answer:
Yes. When the object is placed at a distance less than the focal length of the mirror we do not get an ¡mage on the screen.

Page 11

Question 16.
Have you observed the rearview mirrors of a car?
Answer:
Yes. I have observed rear view mirror of a car.

Question 17.
What type of surface do they have?
Answer:
A concave mirror will be like the rubber sole bent inwards and the reflecting surface will be curved inwards.

Question 18.
Can we draw ray diagrams for convex surface?
Answer:
We can draw ray diagrams with convex surface by making use of “easy” rays that we have identified, with small modifications.

Think and discuss 

Question 1.
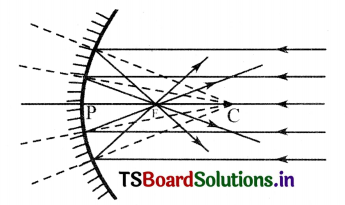
See the figure – 5 In text. A set of parallel rays are falling on a convex mirror. What conclusions can you draw from this?
Answer:
On seeing figure 5, the following conclusions can be drawn;

1. The parallel beam of rays meet at infinity.
2. So the Image Is not visible. :
3. This parallel beam of rays forms a virtual image which is smaller than the size of object.

Question 2.
Will you get a point Image If you place a paper at the focal point?
Answer:
No. These parallel beam of rays do not meet at a visible point and we do not get a point image.

Question 3.
Do you get an image when object is placed at F? Draw a ray diagram. Do the experiment.
Answer:
We did not get the image when the object is placed at Focus ‘F’ of concave mirror.
Experiment:
Aim: Observing the Image formed by the object which is placed at ‘F’ of concave mirror.
Materal required: A candle, paper, a concave mirror (known focal length), V-stand, measuring
tape or meter scale.

Procedure:
1. Place the concave mirror on V-stand, a candle and meter scale as shown in figure.

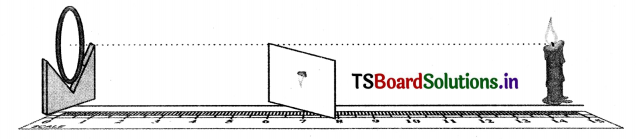
2. Keep the candle at a distance equal to the focal length of the mirror. (which Is known)
3. Now move the paper screen away from the mirror along the axis to observe the image.
4. You will notice that the image cannot be seen because it Is formed at infinity.

TS 10th Class Physical Science Reflection of Light at Curved Surfaces Activities

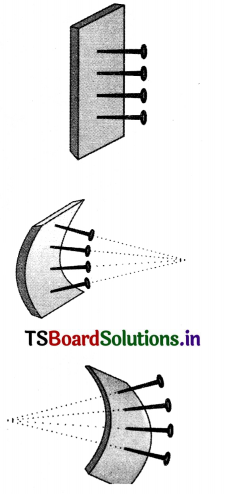
Activity 1

Question 1.
Explain an activity to find the normal to a curved surface.
Answer:

1. Take a small piece of thin foam or rubber.
2. Put some pins in a straight line on the foam.
3. All these pins are perpendicular to the foam.
4. If the foam is considered as a mirror, each pin would represent the normal at that point.
5. Any ray incident at the point where the pin makes contact with the surface will reflect at the same angle the incident ray made with the pin-normal.
6. Now bend the foam piece inwards.
7. The pins still represent the normal at various poInts.
8. You will observe that all the pins tend to coverage at a point.
9. This will be appear like a concave mirror.
10. Now bend the foam piece outwards.
11. The pins seem to move away from each other that means they diverge.
12. The pins still represent the normal at various points.
13. This will be appear like a convex mirror.
    

Activity 2

Question 2.
How do you Identify the focal point and foal length of a concave mirror?
Answer:
Hold a concave mirror perpendicular to me direction of sunlight

• Take a small paper and slowly move it in front of the mirror.
• Find the point where you get smallest and brigh – test spot, which is the image of the sun.
• The rays coming from the sun parallel to the concave mirror are converging at a point. This point is called focus or focal point (F) of the concave mirror.
• Measure the distance of this spot from the pole (P) of the mirror.
• ThIs distance Is the focal length (f) of the mirror

Lab Activity

Question 1.
Describe an experiment to observe types of mages formed by e concave mirror and measure the object end image distances.
(OR)
Write the experimental method in measuring the distances of object and image using concave mirror. And write the table For observations.
Answer:
Aim: Observing the types of images and reasoning the object distance and image distance from the concave mirror.
Material required: A candle, paper, concave minor (known focal length), V- stand, moesunng tape or meter scale.
Procedure
1. Place the concave mirror on V-stand, a candle and meter scale as shown in figure.

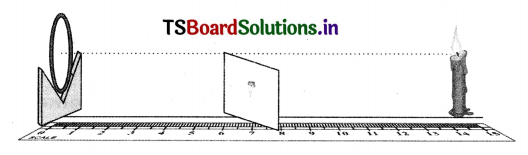
2. Keep the candle at different distances from the mIrror (10 cm to 80 cm) along the axis and by moving the paper screen fd the position where you get the sharp mage on paper.
3. Note down your observations in the following table.

4. Since we know the focal point and centre of curvature, we can re-classify our above observations as shown in the following table.

Students can practice TS 6th Class Maths Solutions Chapter 1 Knowing Our Numbers Ex 1.1 to get the best methods of solving problems.

TS 6th Class Maths Solutions Chapter 1 Knowing Our Numbers Exercise 1.1

Question 1.
Which is the greatest and the smallest among the following numbers ?
(i) 15432, 15892, 15370, 15524
Answer:
All the four numbers are of 5 digits.
The digits in ten thousands place in all the given numbers are same.
The digits in thousands place are also same.
So we move to hundreds place to compare them.
The digits in hundreds place are 4, 8, 3 and 5 respectively.
∴ 3 < 4 < 5 < 8
∴ The greatest number is 15892
The smallest number is 15370

(ii) 25073, 25289, 25800, 25623
Answer:
All the four numbers are of 5 digits. The digits in ten thousands place in all the given numbers are same. The digits in thousands place are also same. So we move to hundreds place to compare them.
The digits in hundreds place are 0, 2, 8, 6 respectively.
∴ 0 < 2 < 6 < 8
The greatest number is 25800
The smallest number is 25073

(iii) 44687, 44645, 44670, 44602
Answer:
All the four numbers are of 5 digits.
The digits in ten thousands place, thousands place and hundreds place are same in all the numbers.
So we move to tens place to compare them.
The digits in tens place are 8, 4, 7, 0 respectively.
∴ 0 < 4 < 7 < 8
∴ The greatest number is 44687.
The smallest number is 44602.

(iv) 75671, 75635, 75641, 75610
Answer:
All the four numbers are of 5 digits. The digits in ten thousands place, thousands place and hundreds place are same in all the numbers. So we move to tens place to compare them. The digits in tens place are 7, 3, 4, 1 respectively.
∴ 1 < 3 < 4 < 7
∴ The greatest number is 75671 The smallest number is 75610

v) 34895, 34891, 34899, 34893
Sol. All the four numbers are of 5 digits. The digits in ten thousands place, thousands place, hundreds place and tens place are same in all the numbers. So we move to units place to compare them.
The digits in units place are 5, 1, 9, 3 respectively.
∴ 1 < 3 < 5 < 9
∴ The greatest number is 34899
The smallest number is 34891

Question 2.
Write the numbers in ascending (in-creasing) order.
(i) 375, 1475, 15951, 4713
Answer:
We can say that 15951 is the greatest number and 375 is the smallest number by counting the digits in the numbers. Regarding 1475 and 4713 it is clear that 1475 < 4713
∴ 375 < 1475 < 4713 < 15951
The ascending order is 375, 1475, 4713, 15951

(ii) 9347, 19035, 22570, 12300
Answer:
The number with four digits (i.e.,) 9347 is the smallest number because the other numbers are of five digits.
In 19035, 22570, 12300 numbers, the greatest number is 22570.
Again 12300 < 19035
∴ 9347 < 12300 < 19035 < 22570
The ascending order is 9347, 12300, 19035, 22570

Question 3.
Write the numbers in descending (decreasing) order.
(i) 1876, 89715, 45321, 89254
Answer:
1876 is the smallest number because it has four digits while the other numbers are of five digits.
The other numbers are 89715, 45321, 89254.
45321 < 89254 < 89715 (∵ 2 < 7) ∴ The descending order is 89715, 89254, 45321, 1876. (∵ 89715 > 89254 > 45321 > 1876)

(ii) 3000, 8700, 3900, 18500
Answer:
18500 is the greatest number because it has five digits while the other numbers are of four digits.
The other numbers are 3000,8700,3900
3000 < 3900 < 8700 ∴ The descending order is 18500, 8700, 3900, 3000. (∵ 18500 > 8700 > 3900 > 3000)

Question 4.
Compare the numbers by placing appropriate symbol (< or >) in the space given.
(i) 3854 ………………… 15200
Answer:
3854 < 15200 (ii) 4895 …………………. 4864 Answer: 4895 > 4864

(iii) 99454 ………………….. 99445
Answer:
99454 > 99445

(iv) 14500 ………………….. 14499
Answer:
14500 > 14499

Question 5.
Write the numbers in words :
(i) 72642
Answer:
72,642 = Seventy two thousand six hundred forty two

(ii) 55345
Answer:
55,345 = Fifty five thousand three hundred forty five

(iii) 66600
Answer:
66,600 = Sixty six thousand six hundred

(iv) 30301
Answer:
30,301 = Thirty thousand three hundred one

Question 6.
Write the numbers in figures:
(i) Forty thousand two hundred seventy.
Answer:
40,270

(ii) Fourteen thousand sixty four.
Answer:
14,064

(iii) Nine thousand seven hundred.
Answer:
9,700

(iv) Sixty thousand.
Answer:
60,000

Question 7.
Form four digit numbers with the digits 4, 0, 3, 7 and find which is the greatest and the smallest among them ?
Answer:
The digits given are 4, 0, 3, 7.
The four digit numbers formed with the digits are
4037, 4073, 4370, 4307, 4730, 4703
3047, 3074, 3470, 3407, 3704, 3740
7034, 7043, 7304, 7340, 7403, 7430
The greatest number is 7430
The smallest number is 3047

Question 8.
Write the following numbers.
(i) the smallest four digit number
Answer:
1000

(ii) the greatest four digit number
Answer:
9999

(iii) the smallest five digit number
Answer:
10000

(iv) the greatest five digit number
Answer:
99999