TS 10th Class Maths Solutions Chapter 5 Quadratic Equations InText Questions

Students can practice 10th Class Maths Solutions Telangana Chapter 5 Quadratic Equations InText Questions to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 5 Quadratic Equations InText Questions

Try This

Question 1.
Check whether the following equations are quadratic or not.
i) x² – 6x – 4 = 0
ii) x³ – 6x² + 2x – 1 = 0
iii) 7x = 2x²
iv) x² + \(\frac{1}{\mathrm{x}^2}\) = 2
v) (2x + 1) (3x + 1) = 6(x – 1)(x – 2)
vi) 3y² = 192 (Page No. 102)
Solution:
i) x² – 6x – 4 = 0
Yes, It’s a quadratic equation.

ii) x³ – 6x² + 2x – 1 = 0
No, It is not a quadratic equation.
[∵ degree is 3]

iii) 7x = 2x²
Yes, It’s a quadratic equation.

iv) x² + \(\frac{1}{x^2}\) = 2
No, It is not a quadratic equation.
[∵ degree is 4]

v) (2x + 1) (3x + 1) = 6(x – 1) (x – 2)
No, It is not a quadratic equation.
[coefficient of x² on both sides is same i.e., 6]

vi) 3y² = 192
Yes, It’s a quadratic equation.

Try This

Question 1.
Verify whether 1 and \(\frac{3}{2}\) are the roots of the equation 2x² – 5x + 3 = 0. (Page No. 107)
Solution:
Let the given
Q.E. be p(x) = 2x² – 5x + 3
Now p(1) = 2(1)² – 5(1) + 3
= 2 – 5 + 3 = 0
∴ 1 is a root of 2x² – 5x + 3 = 0
also p(\(\frac{3}{2}\)) = 2(\(\frac{3}{2}\))² – 5(\(\frac{3}{2}\)) + 3
= 2 × \(\frac{9}{4}\) – \(\frac{15}{2}\) + 3
= \(\frac{9}{2}\) + 3 – \(\frac{15}{2}\) = \(\frac{9+6-15}{2}\) = 0
∴ \(\frac{3}{2}\) is also a root of 2x² – 5x + 3 = 0

Do This

Question 1.
Solve the equations by completing the square. (Page No. 113)

i) x² – 10x + 9 = 0
Solution:
Given x² – 10x + 9 = 0
⇒ x² – 10x = – 9
⇒ x² – 2. x. 5 = – 9
⇒ x² – 2.x. 5 + 5² = -9 + 5²
⇒ (x – 5)² = 16
∴ x – 5 = ± 4
∴ x – 5 = 4 (or) x – 5 = – 4
⇒ x = 9 (or) x = 1
⇒ x = 9 (or) 1

ii) x² – 5x + 5 = 0
Solution:
Given : x² – 5x + 5 = 0
⇒ x² – 5x = -5

iii) x² + 7x – 6 = 0
Solution:
x² + 7x – 6 = 0
x² + 7x = 6
x² + 2.x.\(\frac{7}{2}\) = 6
x² + 2.x.\(\frac{7}{2}\) + (\(\frac{7}{2}\))² = 6 + (\(\frac{7}{2}\))²

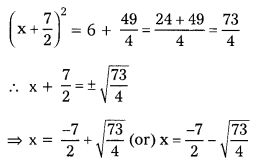
Think – Discuss

Question 1.
We have three methods to solve a quadratic equation. Among these three, which method would you like to use ? Why ? (Page No. 115)
Solution:
If the Q.E. has district and real roots, we use factorisation. If Q.E. has no real roots, we use quadratic formula.

Try This

Question 1.
Explain the benefits of evaluating the discriminate of a quadratic equation before attempting to solve it. What does its value signifies ? (Page No. 122)
Solution:
The discriminant b² – 4ac of a Q.E. ax² + bx + c = 0 give the clear idea about the nature of Q the roots of the Q.E. If the discriminant D = b² – 4ac > 0, the Q.E. has distinct and real roots.

If b² – 4ac = 0, the Q.E. had equal roots. If b² – 4ac < 0, the Q.E. has no real roots. By the 3 value of the discriminant, we can state the nature of the roots of a Q.E. without actually finding them.

Question 2.
Write three quadratic equations one having two distinct real solutions, one having no real solution and one having exactly one real solution. (Page No. 122)
Solution: