TS 10th Class Maths Solutions Chapter 3 Polynomials InText Questions

Students can practice 10th Class Maths Solutions Telangana Chapter 3 Polynomials InText Questions to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 3 Polynomials InText Questions

Do this

Question 1.
State which of the following are polynomials and which are not ? Give reasons. (Page No. 48)
(i) 2x³
(ii) \(\frac{1}{x-1}\)
(iii) 4z² + \(\frac{1}{7}\)
(iv) m² – \(\sqrt{2}\) m + 2
(v) p^-2 + 1
Solution:
i) 2x³ is a polynomial
ii) \(\frac{1}{x-1}\) is not a polynomial.
iii) 4z² + \(\frac{1}{7}\) is a polynomial.
iv) m² – \(\sqrt{2}\)m + 2 is a polynomial.
v) p^-2 + 1 is not a polynomial.

Question 2.
p(x) = x² – 5x – 6, find the values of p(1), p(2), p(3), p(0), p(-1), p(-2), p(-3). (Page No. 49)
Solution:
p(x) = x² – 5x – 6
p(1) = (1)² – 5(1) – 6 = 1 – 5 – 6 = 1 – 11 = -10
p(2) = (2)² – 5(2) – 6 = 4 – 10 – 6
= 4 – 16 = – 12
p(3) = (3)² – 5(3) – 6 = 9 – 15 – 6
= 9 – 21 = -12
p(0) = (0)² – 5(0) – 6 = 0 – 0 – 6 = 0 – 6 = -6
p(-1) = (-1)² – 5(-1) – 6 = 1 + 5 – 6 = 6 – 6 = 0
p(-2) = (-2)² – 5(-2) – 6 = 4 + 10 – 6 = 8
p(-3) = (-3)² – 5(-3) – 6 = 9 + 15 – 6
= 24 – 6 = 18

Question 3.
p(m) = m² – 3m + 1, find the value of p(1) and p(-1). (Page No. 49)
Solution:
p(m) = m² – 3m + 1
p(1) = (1)² – 3(1) + 1 = 1 – 3 + 1 = 2 – 3 = -1
p(-1) = (-1)² – 3(-1) + 1 = 1 + 3 + 1 = 5

Question 4.
Let p(x) = x² – 4x + 3. Find the value of p(0), p(1), p(2), p(3) and obtain zeroes of the polynomial p(x).
(Page No. 50)
Solution:
p(x) = x² – 4x + 3
p(0) = (0)² – 4(0) + 3 = 0 – 0 + 3 = 3
p(1) = (1)² – 4(1) + 3 = 1 – 4 + 3 = 4 – 4 = 0
p(2) = (2)² – 4(2) + 3 = 4 – 8 + 3 = 7 – 8 = -1
p(3) = (3)² – 4(3) + 3 = 9 – 12 + 3 = 12 – 12 = 0
We see that p(1) = 0 & p(3) = 0
These points x = 1 & x = 3 are called zeroes of the polynomial p(x) = x² – 4x + 3

Question 5.
Check whether -3 and 3 are the zeroes of the polynomial x² – 9. (Page No. 50)
Solution:
p(x) = x² – 9 ⇒ p(-3) = (-3)² – 9 = 9 – 9 = 0
p(3) = (3)² – 9 = 9 – 9 = 0
p(-3) = 0 & p(3) = 0
∴ -3 and 3 are the zeroes of the polynomial p(x) = x² – 9

Try This

Question 1.
Write 3 different quadratic, cubic and 2 linear polynomials with different number of terms. (Page No. 48)
Solution:
3 different quadratic polynomials :

1. 3x² + 2x + 4
2. 5x² + x + 1
3. x² – 3x + 2

3 different cubic polynomials :

1. x³ + 2x² + x + 1
2. 3x³ + 2x + 1
3. x³ + 1

2 linear polynomials :

1. 4x + 3
2. 3x + 2

Question 2.
Write a quadratic polynomial and a cubic polynomial in variable x in the general form. (Page No. 49)
Solution:
General form of a (in variable x)

1. Quadratic polynomial → ax² + bx +c.
2. Cubic polynomial → ax³ + bx² + cx + d

Question 3.
Write a general polynomial q(z) of degree n with coefficients that are b₀,…,b_n. What are the conditions on b₀, ..,b_n ? (Page No. 49)
Solution:
General polynomial q(z) of degree ‘n’ is q(z) = b₀xⁿ + b₁x^n-1 + b₂x^n-2 + b₃x^n-3 +…. +b_n-1x + b_n

Conditions :

1. b₀, b₁, b₂, …….,b_n-1, b_n are real coefficients.
2. bg ≠ 0

Do This

Question 1.
Draw the graph of
(i) y = 2x + 5
(ii) y = 2x – 5
(iii) y = 2x and find the point of intersection on X-axis. Is the x- coordinate of these points also the zero of the polynomial ? (Page No. 52)

i) y = 2x +


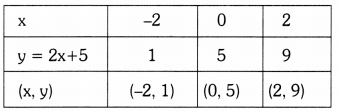
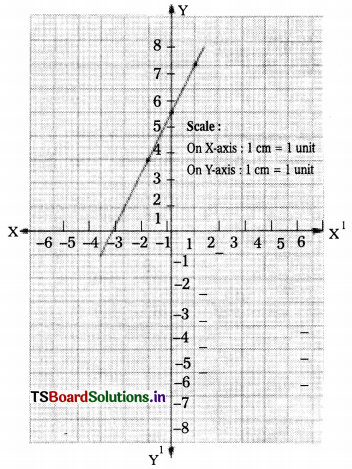
The zero of the polynomial 2x + 5 is the x-coordinate of the point where the graph of y = 2x + 5 intersects the X-axis.
∴ Zero of the polynomial 2x + 5 is \(\frac{-5}{2}\).

ii) y = 2x – 5

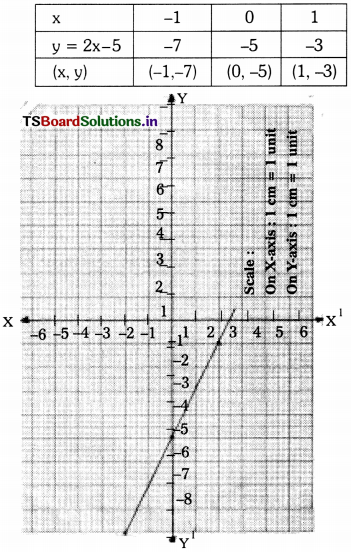
The zero of the polynomial 2x – 5 is the x-coordinate of the point where the graph of y = 2x – 5 intersects the X-axis.
∴ Zero of the polynomial 2x – 5 is 5/2.

iii) y = 2x

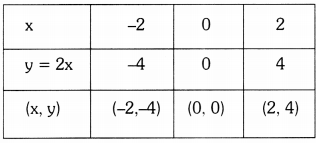
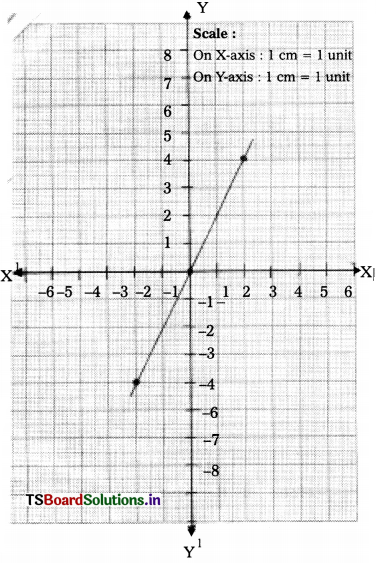
The zero of the polynomial 2x is the x-coordinate of the point where the graph of y = 2x intersects the X-axis.
The graph y = 2x does not intersect X-axis.
∴ There is no zero of the polynomial for 2x.

Try This

Question 1.
Draw the graphs of
(i) y = x² – x – 6
(ii) y = 6 – x – x² and find zeroes in each case. What do you notice ? (A.P. Mar. 15) (Page No. 53)
Solution:
i) y = x² – x – 6

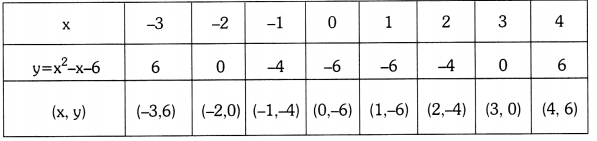
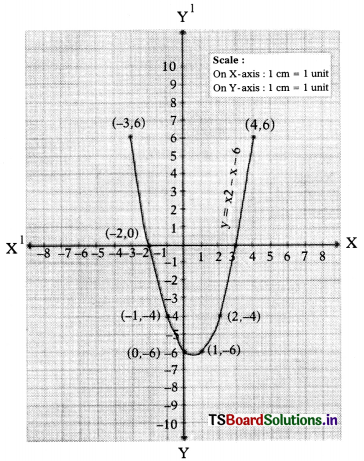
Zeroes of the quadratic polynomial x² – x – 6 are the x-co-ordinates of the points of X-axis.

-2 & 3 are zeroes of the quadratic polynomial and -2 & 3 are intersections points of X-axis.

ii) y = 6 – x – x²

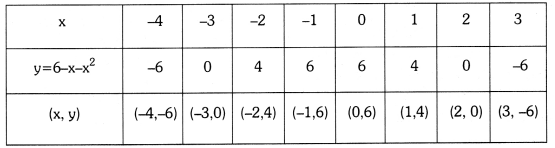
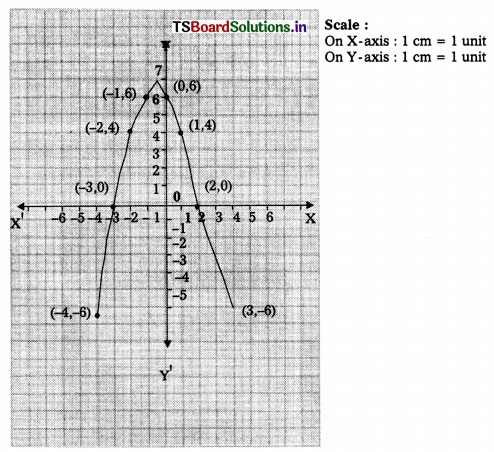
Zero of the quadratic polynomial 6 – x – x² are the x-coordinates of the points of X-axis.
-3 & 2 are zeroes of the quadratic polynomial and -3 & 2 are intersection points of X-axis.

Observations : The graph cuts X-axis at two distinct points.
The parabola can open either upward or down-ward.

Question 2.
Write three quadratic polynomials that have 2 zeroes each. (Page No. 55)
Answer:

1. y = x² + 5x + 6
2. y = x² – 5x + 6
3. y = 2x² + x – 1

The above three polynomials have 2 zeroes each.

Question 3.
Write one quadratic polynomial that has one zero. (Page No. 55)
Answer:
y = x + 2 this polynomial has one zero.

Question 4.
How will you verify if a quadratic polynomial it has only one zero ?(Page No. 55)
Answer:
The linear polynomial ax + b, a ≠ 0 has exactly one zero namely the x co-ordinate of the point where the graph of y = ax + b intersects X-axis. Every linear polynomial in ax + b, a ≠ 0 has exactly one zero.

Question 5.
Write three quadratic polynomials that have no zeroes for x that are real numbers. (Page No. 55)
Answer:

1. y = 8x² – 6x + 1
2. y = x² – 8x + 17
3. y = x² – 4x + 5

These polynomials have no zeroes for x.

Question 6.
Find the zeroes of cubic polynomials
(i) -x³
(ii) x² – x³
(iii) x³ – 5x² + 6x without drawing the graph of the polynomial. (Page No. 57)
Solution:
i) p(x) = -x³.
p(x) = 0
-x³ = 0
x³ = 0
x = 0. So ‘0’ is the zero of the polynomial -x³.

ii) p(x) = x² – x³
= x²(1 – x)
p(x) = 0
x²(1 – x) = 0 ⇒ x² = 0 or 1 – x = 0
x = 0 (or) x = 1
0 & 1 are the zeroes of the polynomial x² – x³

iii) p(x) = x³ – 5x² + 6x
= x(x² – 5x + 6)
= x(x² – 3x – 2x + 6)
= x[x(x-3) – 2(x – 3)]
= x[(x – 3) (x – 2)]
p(x) =0
x[(x – 3) (x – 2)] = 0 ⇒ x = 0, x – 3 = 0
⇒ x = 3, x – 2 = 0 ⇒ x = 2.
∴ 0, 2 and 3 are the zeroes of the polynomial x³ – 5x² + 6x

Do This

Question 1.
Find the zeroes of the quadratic polynomials given below. Find the sum and product of the zeroes and verify relationship to the coefficients of terms in the polynomial .
(i) p(x) = x² – x – 6
(ii) p(x) = x² – 4x + 3
(iii) p(x) = x² – 4
(iv) p(x) = x² + 2x + 1. (Page No. 62)
Solution:
i) The given polynomial is x² – x – 6.
x² – x – 6 = x² – 3x + 2x – 6
= x(x – 3) +2(x – 3)
= (x + 2) (x – 3)
So, the value of x² – x – 6 is zero when x + 2 = 0 or x – 3 = 0 (i.e.,) when x = -2 or x = 3
Therefore, the zeroes of x² – x – 6 are -2 & 3
Now, sum of the zeroes = -2 + 3 = 1

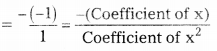
Product of the zeroes = -2 × (3) = -6

ii) The given polynomial is x² – 4x + 3. (A.P. Mar. June 15)
x² – 4x + 3 = x² – 3x – x + 3
= x(x – 3) -1(x – 3)
= (x – 1) (x – 3)
So, the value of x² – 4x + 3 is zero when (x – 1) = 0 or (x – 3) = 0
(i.e.,) when x = 1 or x = 3
∴ The zeroes of x – 4x + 3 are 1 & 3.
Now sum of zeroes = 1 + 3 = 4

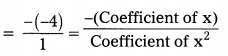
Product of the zeroes = 1 × 3 = 3

iii) The given polynomial is x² – 4
x² – 4 = (x)² – (2)² = (x + 2) (x – 2)
So, the value of x² – 4 is zero when (x + 2) = 0 or (x – 2) = 0
(i.e.,) when x = -2 or x = 2
∴ The zeroes of x² – 4 are -2 & 2.
Now, sum of the zeroes = -2 + 2 = 0

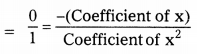
Product of the zeroes = (-2) × (2) = – 4

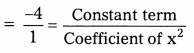
iv) The given polynomial is x² + 2x + 1.
x² + 2x + 1 = x² + x + x + 1
= x(x +1) +1 (x + 1)
= (x + 1) (x + 1)
= (x + 1)²
So, the value of x² + 2x + 1 is zero when (x + 1) = 0 = x + 1 = 0 (i.e.,) when x = -1 & x = -1.
∴ The zeroes of the polynomial are -1 & -1. Now, sum of the zeroes = -1 + (-1)
= -1 -1 = – 2

Question 2.
If α, β, γ are the zeroes of the given cubic polynomials, find the values as given in the table. (Page No. 66)

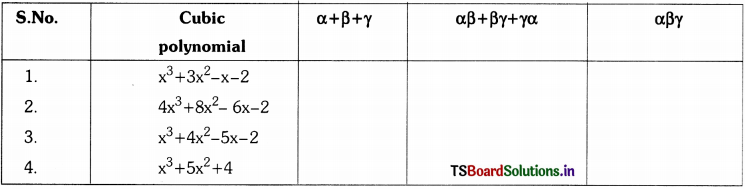
Solution:

Try This

Question 1.
i) Find a quadratic polynomial with zeroes -2 and 1/3. (Page No. 64)
Solution:
Let the quadratic polynomial be ax² + bx + c, a ≠ 0 & its zeroes be α & β.
Here α = -2; β = 1/3
sum of the zeroes = (α + β)
sum of the zeros = (α + β)
= (-2) + \(\frac{1}{3}\) = \(\frac{-6+1}{3}\) = –\(\frac{5}{3}\)
Product of the zeroes = αβ = (-2)(\(\frac{1}{3}\))
= –\(\frac{2}{3}\)
∴ The quadratic polynomial
ax² + bx + c is
k[x² – (α + β)x + αβ] where k is a constant.
= k[x² – \(\left(\frac{-5}{3}\right)\)x + \(\left(\frac{-2}{3}\right)\)]
We can put different values of k.
When k = 3 the quadratic polynomial will be 3x² + 5x – 2.

ii) What is the quadratic polynomial whose sum of zeroes is \(\frac{-3}{2}\) and the product of zeroes is -1 ? (Page No. 64) (A.P. June’15)
Solution:
Sum of zeroes = (α + β) = \(\frac{-3}{2}\)
Product of zeroes = αβ = -1
∴ The quadratic polynomial
ax² + bx + c is k[x² – (α + β)x + αβ]
We can put different values of k.
When k = 2 the quadratic polynomial will be 2x² + 3x – 2.