TS Inter 2nd Year Maths 2B Circles Important Questions

Students must practice these TS Inter 2nd Year Maths 2B Important Questions Chapter 1 Circles to help strengthen their preparations for exams.

TS Inter 2nd Year Maths 2B Circles Important Questions

Very Short Answer Type Questions      

Question 1.
Find the equation of circle with centre (1, 4) and radius 5.
Solution:
Standand equation of circle with centre
(h. k) and radius ‘r’ is (x – h)² + (y – k)² r²
(h, k) = (1, 4) and r= 5
∴ Equation of circle is (x – 1)² + (4)² = 25
x². y² -2x – 8y+ 17=25
= x²+y²– 2x – 8y – 8 = 0

Question 2.
Find the centre and radius of the circle
x² + y² + 2x – 4y – 4 = 0.
Solution:
Comparing with x²+y²+2gx+2fy+c = 0
2g=2, 21= – 4, and c = – 4
∴ Centre=(-g,-f)=(-1,2) and
∴ Radius = \(\sqrt{g^2+f^2-c}=\sqrt{1+4+4}=3\)

Question 3.
Find the centre and radius of the circle
3x² + 3y² – 6x + 4y – 4 = 0.
Solution:
Given equation can be written as

Question 4.
Find the equation of the circle whose centre is (-.1, 2) and which passes through (5,6).
Solution:
Let C (-1, 2) be the centre of the circle. Since (5, 6) is a point on the circle, the radius of the circle.

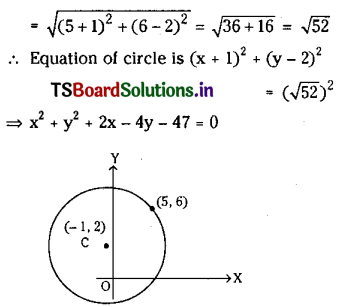
Question 5.
Find the equation of circle passing through (2,3) and concentric with the circle
x² + y² + 8x + 12y + 15 = 0.
Solution:
Let the equation of required circle be
x² + y² + 2gx + 2fy + c‘ = 0
If It passes through (2, 3) then
4+9+8(2)+ 12(3) + c‘ = 0
= 65 + c’ = 0 ⇔ c’ = – 65
∴ The equation of required circle is x² + y² + 8x + 12y – 65 = 0.

Question 6.
If the circle x² + y² +ax+by -12 = 0 has the centre at (2,3) then find a, b and the radius of the circle.
Solution:
The equation of circle is
x² + y² +ax+by -12 = 0
Centre 01 the circle = \(\left(\frac{-\mathrm{a}}{2},-\frac{\mathrm{b}}{2}\right)\) = (2, 3) (given)
∴ a =- 4 and b = – 6
∴ Radius of the circle = \(\sqrt{4+9+12}=5\)

Question 7.
If the circle x² + y² – 4x+6y+a = 0 has radius 4 then lead ‘a’.
Solution:
Given equation of circle is
x² + y² – 4x + 6y+a = 0,
centre C = (2, -3) and radius = 4 (given)
∴ \(\sqrt{4+9-\mathrm{a}}\) = 4 ⇒ 13 – a = 16 ⇒ a – 3.

Question 8.
Find the equation of the circle whose extremities of diameter are (1, 2) and (4, 5).
Solution:
Taking A(1, 2) (x₁,y₁) and B(4, 5) (x₂,y₂) the equation of circle having A, B as extremities of diameter is
(x-x₁)(x-x₂)+(y-y₁)(y-y₂)=0
(x – 1)(x-4) + (y-2)(y-5) =0
= x²-5x+4+y²-7y+ 10 =0
= x²+y²-5x-7y+ 14=0

Question 9.
Find the other end of the diameter of the circle x² + y²-8x – 8y + 27 = 0 if one end of it is  (2, 3).
Solution:
Centre of the given circle is C (4, 4).
One end of diameter is A = (2, 3). Let the other end be B (x, y). Then C is the end point of AB.
∴ \(\frac{x+2}{2}=4 \) and \( \frac{y+3}{2}=4\)
⇒ x = 6, y = 5
∴ Other end of the diameter B = (6, 5)

Question 10.
Obtain the parametric equations of x² + y² = 1.
Solution:
Centre of the circle = (0, 0) and radius = 1 = (h, k)
The parametric equations of curve are
x = h + rcosθ = 0 + 1. cosθ = cosθ
y = k + rsinθ = θ+1.sinθ = sinθ
0 ≤ θ ≤ 2π

Question 11.
Obtain the parametric equation of the circle represented by x² + y² + 6x + 8y – 96 = 0.
Solution:
Centre(h,k) =(-3,-4)
and radius r = \(\sqrt{9+16+96}=\sqrt{121}\) = 1
∴ x = h + r cosθ = – 3 + 11 cosθ
y = k + r sin 0=- 4 + 11 sin θ,0≤0≤ 2π

Question 12.
Locate the position of the point (2, 4) w.r.t circle x² + y² – 4x – 6y + 11 = 0.
Solution:
Here (x, y) (2, 4) and
x² + y² – 4x – 6y+ 11=0
S ≡ (2)²+(4)²– 8 – 12 +11=-1
Since S₁₁ <0, the point (2, 4) lies Inside the circle.

Question 13.
Find the length of the tangent from (1,3) to the circle x² + y² -2x + 4y – 11 = 0.
Solution:
Given (x₁, y₁) = (1, 3) and
S ≡ x²+y²-2x+4y-11 = 0
S₁₁ = 1²+3² -2 + 12 – 11 = 9
∴ Length of the tangent from P(x₁, y₁) to S = 0 is
= \(\sqrt{S_{11}}=\sqrt{9}\) = 3

Question 14.
Show that the circle S ≡ x² + y²+2gx+2fy+ c = 0 touches (i) x-axis if g² = c (ii) Y-axis if f² =c.
Solution:
(i) We have the Intercept made by S = 0 on X-axis is \(2 \sqrt{\mathrm{g}^2-\mathrm{c}}\).
If the circle touches X-axis then \(2 \sqrt{\mathrm{g}^2-\mathrm{c}}\) = ⇒ g²= c.

(ii) Similarly if the intercept made by S = 0 on
Y-axis is \(2 \sqrt{f^2-c}\) . If the circle touches Y-axis then \(2 \sqrt{f^2-c}\) = f²=c.

Question 15.
Find the equation of tangent to x² + y² – 6x +4y – 12 = 0 at (-1,1).
Solution:
We have the equation of tangent at (x₁, y₁) to
S = 0 is xx₁ +yy₁ +g(x+x₁)+1(y+y₁)+ c
⇒ x(-1) 4y(1) – 3(x-1) + 2(y+ 1)-12 = 0
⇒ – 4x+3y-7 = 0 ,
⇒ 4x – 3y+ 7 = 0

Question 16.
Show that the line 5x + 12y – 4 = 0 touches the circle x² + y² – 6x + 4y + 12 = 0.
Solution:
Centre of the given circle = (3, -2) and
radius = \(\sqrt{9+4-12}=1\)
The perpendicular distance from the centre
(3,-2) to the line 5x + 12y- 4 = 0 is
\(=\left|\frac{5(3)+12(-2)-4}{\sqrt{25+144}}\right|=\left|\frac{-13}{13}\right|=1\)
∴ radius of the circle.
⇒ The line 5x + 12y-.4 = 0 touches the given circle.

Question 17.
Find the area of the triangle formed by the tangent at P(x₁, y₁)to the circle x² + y² = a² with the coordinate axes where x₁ y₁ ≠ 0.
Solution:
Equation of tangent at (x₁, y₁) to the circle
x² +y²-a² is xx₁ +yy₁– a²=0.
x, y intercepts are \(\frac{a^2}{x_1}\) and \(\frac{\mathrm{a}^2}{\mathrm{y}_1}\)
∴ Required area of the triangle
=\(\frac{1}{2}\left|\frac{a^2}{x_1} \cdot \frac{a^2}{y_1}\right|=\frac{a^4}{2\left|x_1 y_1\right|}\)

Question 18.
State the necessary and sufficient condition forlx+ my + 0 to be normal to the circle x²+ y² + 2gx + 2fy + c = 0.
Solution:
The straight line lx + my + n = 0 is a normal to the circle S ≡ x² + y² + 2 + 2fy + c = 0.
⇔ Centre (-g, – f) of the circle lies on lx + my + n = 0
⇔ l(-g) + m(-f) + n = 0
⇔ lg + mf = n

Question 19.
Find the condition that the tangents are drawn from the exterior point (g,f) to S ≡ x²+y²+ 2gx + 2fy + c= 0 are perpendicular to each other.
Solution:
If the angle between the tangents drawn from P(x₁,y₁) to S=0 is θ then

Question 20.
Find the chord of contact of (2, 5) with respect to the circle x² + y² – 5x + 4y -2 = 0.
Solution:
2g=-5 and 2f = 4 ⇒ g\(\frac{5}{2}\) and f=2,c=-2
Equation of chord of contact of (x₁, y₁) w.r.t S = 0 is
xx₁ +yy₁ + g(x+x,) +f(y+y₁)+c=0
=2x+5y-(x+2)+2(y+5)-2=0
= x-14y+6=0

Question 21.
Find the equation of the polar of the point (2, a)w.r.tthe circle x²+y²+6x +8y-96 =0.
Solution:
Equation of polar of (x₁, y₁) (2, 3) is +yy +g(x+x₁)+f(y+y₁)+c=0
⇒ x(2) +y(3)+ 3(x + 2) +.4(y+ 3)- 96 = 0
⇒ 5x + 7y – 78 = 0
⇒ (x₁– a)²= (x₁ +a)²+y²
⇒ (x₁ – a)² – (x₁ + a)² y²₁
⇒ y – 4ax₁ ⇒ y²₁ + 4ax₁ = 0
∴ Locus of (x₁, y₁) is y² + 4ax = 0.

Question 22.
Find the pole of the line x+y+2 = 0 w.r.t x² + y²– 4x + 6y – 12=0.
Solution:
Here lx +my+n=0 is x+y+2=0 and S=0 is x² + y² – 4x + 6y – 12 = 0.

Question 23.
Show that (4, -2) and (3, -6) are conjugate w.r.t. the circle x² + y² – 24 = 0.
Solution:
Here (x₁, y₁) = (4, – 2) and (x₂, y₂) (3, -6) and S = x² + y²-24 = 0 ……….. (1)
Two points (x₁, y₁) and (x₂, y₂) are conjugate w.r.t S=0 if S₁₂=0
∴ x₁x₂+y₁y₁-24 = 0
For the given points
S₁₂ =4(3)+(-2)(-6)-24-0
∴ The given points are conjugate w.r.t the given circle.

Question 24.
If (4, k) and (2,3) are conjugate points w.r.t x² + y² = 17 then find k.
Solution:
(x₁, y₁)= (4, k) and (x₂, y₂)= (2, 3). Since the given points are conjugate S₁₂ = 0.
= x₁x₂ + y₁y₂ – 17 = 0
(4)(2)+(k)(3)-17=0 ⇒ k=3

Question 25.
Show that the lines 2x+3y+ 11 =0,and 2x – 2y -1= 0 are conjugate w.r.t x² + y²+ 4x + 6y + 12 = 0.
Solution:

Question 26.
Find the inverse point of (2, -3) wrt the circle x²+y²– 4x-6y+9=0
Solution:
Let P(-2, 3) and C (2,3) is the centre of the given circle. Then the polar of P is
x(-2)+y(3)-2(x-2)-3(y+3)+9=0
x = 1 ……………. (1)
Equation of line \(\overline{\mathrm{CP}}=\mathrm{y}-3=\frac{3-3}{2+1}(\mathrm{x}+2)\)
⇒ y – 3 = 0 ⇒ y = 3 ……………. (2)
∴ From (1) and (2) the inverse point of
P(-2, 3) is (1, 3).

Short Answer Type Questions

Question 1.
From the point A(0, 3) on the circle x² + 4x +(y-3)²= 0 a chord AB is drawn and extended to a point M such that
AM = 2AB. Find the equation to the locus of M.
Solution:

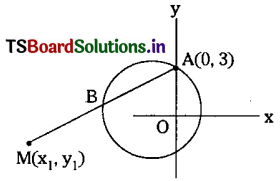
Let M (x₁, y₁) be the locus. Given AM – 2A8
= AB+ BM = AB+AB
BM – AB ⇒ B is the mid point of AM

Question 2.
Find the equation of the circle passing through (4, 1), (6,5) and having the centre on the line 4x+y-16=0.
Solution:
Let the equation of the required circle be
x²+y²+2gx+2fy+c = 0 ……………. (1)
Since it passes through (4, 1) we have
16 + 1 + 8g + 2f + c = 0
= 17+8g+2f+c=0 ……………. (2)
Similarly (6, 5) lies on (1) then
36+25+12g+ 10f +c=0
= 61+12g+10f+c=0 ……………. (3)
Given that the centre of circle (-g, -f) lies on 4x + y-16 = 0
-4g-f-16=0
⇒ 4g+f+16=0 ……………. (4)
From (2) and (3)
– 44 – 4g – 8f 0
=g+2f=- 11  ………….. (5)
From (4) 4g+ f =- 16

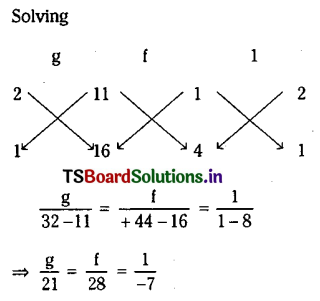
⇒ g= – 3, f =- 4 and
from (2)
17 – 24 – 8+c – 0 ⇒ c = 15
∴ Equation of the required circle from (1) is
x² +y² – 6x – 8y + 15=0.

Question 3.
Suppose a point (x₁, y₁) satisfies x² + y² + 2gx + 2fy + c= 0 then show that it represents a circle whenever g, f and c are real.
Solution:
Comparing the given equation with ax² + 2hxy + by² + 2gx + 2fy + c = 0, we have coefficient of x² = coefficient of y² and coefficient of xy term = 0.
The given equation represents a circle If g² + f² ≥ 0
Since (x₁, y₁) is a point on the circle we have
x₁ + y₁ + 2gx₁ + 2fy₁ + c = 0
g² + f² – c = g² + f² +x²₁ +y²₁ + 2gx₁ + 2fy₁ = (x₁ +g) + (y₁ + f)² ≥ 0
Since g, f and c are real the equation (1) represents a circle.

Question 4.
Find the equation of circle which Louches x-axis at a distance of 3 from the origin and making intercept of length 6 on y-axis.
Solution:

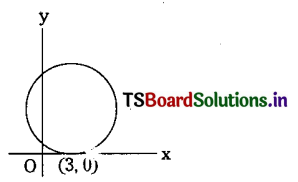
Let the equation of required circle be
x²+y²+2gx+2fy+c=0 …………………….. (1)
If it touches x- axis at (3, 0) then 9 + 0 + 6g + c = 0
⇒ 6g+c= – 9 …………………… (2)
If circle touches x-axis then g² – c = 0 ………………………. (3)
Adding (2) and (3)
g² + 6g = -9
= (g+3)² = 0 = g = -3 ……………………. (4)
∴ From (3), C = 9
Also given that intercept on y-axis is 6

Question 5.
Find the equation of circle which passes through the vertices of the triangle formed by
L₁ =x+y+ 1 =0, L₂=3x+y-5=0 and L₃ = 2x + y-5 = 0.
Solution:
Suppose L₁, L₂; L₂, L.₃ and L₃, L₁ intersect at A, B and C respectively. Consider a curve whose equation is
k(x+y+1)(3x+y-5)+1(3x+y-5)
(2x+y-5)+m(x+y+ 1)
(2x+y-5) = 0 ……………………. (1)
We can verify that this curve passes through A, B, C. So we find k, I and m such that the equation (1) represents a circle. If (1) represents a circle then
(i) coefficient of x² = coefficient of y²
= 3k + 6l + 2m = k + l + m
= 2k+5l+m=0 ………………… (2)
(ii) coefficient of xy is zero.
4k+5l+3m= 0 ………………… (3)
Solving (2) and (3) we get

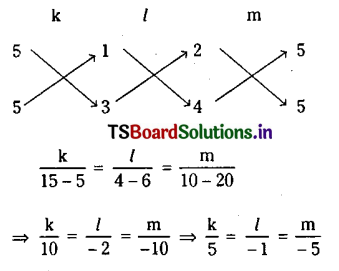
Hence the required equation is
5(x+y+1)(3x+y-5)-1(3x+y-5)
(2x+y-5)-5(x+y+1)
(2x + y -5) = 0
⇒ x²+y²-30x-10y+ 25=0

Question 6.
Find the centre of the drive passing through the points (0,0), (2,0) and (0,2).
Solution:
Let the equation of required circle be
x²+y²+2gx+2fy+c=0 ……………….. (1)
If (1) passes through (0, 0) then c = 0
If (1) passes through (2, 0) then
4+4g+c=0 ………….. (1)
If (1) passes through (0, 2) then
4+4f+c=0 ………….. (2)
From (2) and (3) we have
g=-1 and f = – 1 (∵ c=0)
∴ Centre of the circle = (-g, -f) (1, 1)

Question 7.
If a point P is moving such that the length of tangents drawn from P to x²+y² – 2x + 4y – 20 = 0
x²+y² – 2x-8y+ 1=0 are in the ratio 2: 1 then show that the equation of the locus of P is x²+y² -2x – 12y+8=0.
Solution:
Let P (x₁, y₁) be the locus and \(\overline{\mathrm{PT}_1}, \overline{\mathrm{PT}_2}\) are the tangents drawn from the points P to the two circles x²+y² – 2x + 4y – 20 = 0 and x²+y²– 2x – 8y + 1 = 0

Question 8.
lf S≡ x²+y²+2gx+2fy+c=0 represents a circle then show that the straight line lx + my + n = 0.
(i) touches the circle S = 0 if
\(\left(g^2+f^2-c\right)=\frac{(g l+m f-n)^2}{\left.l^2+m^2\right)}\)

(ii) meets the circle S=0 in two points if.
\(g^2+f^2-c>\frac{(g l+m f-n)^2}{\left.a^2+m^2\right)}\)

(ii) will not meet the circle if
\(\mathrm{g}^2+\mathrm{f}^2-\mathrm{c}<\frac{(\mathrm{g} l+\mathrm{mf}-\mathrm{n})^2}{\left.l^2+\mathrm{m}^2\right)}\)
Solution:
(i) The given straight line lx + my + n = 0
touches the circle S ≡ x²+y² + 2gx + 2fy + c = 0 if the perpendicular distance from (-g, -f) to lx + my + n – 0 is equal to radius r.

(ii) The given line meets the circle S=0 in two points
\(\mathrm{g}^2+\mathrm{f}^2-\mathrm{c}>\frac{(\mathrm{lg}+\mathrm{mf}-\mathrm{n})^2}{l^2+\mathrm{m}^2}\)

(iii) The given line will not meet the circle S=0
If \(\mathrm{g}^2+\mathrm{f}^2-\mathrm{c}<\frac{(\mathrm{gl} l \mathrm{mf}-\mathrm{n})^2}{l^2+\mathrm{m}^2}\)

Question 9.
Find the length of the chord intercepted by the circle x²+y²+8x-4y – 16 = 0 on the line 3x-y+4 = 0.
Solution:

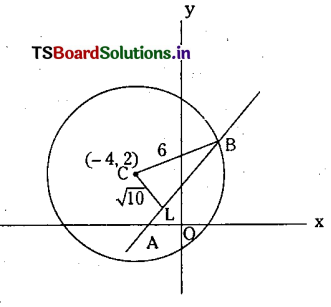
Centre of the circle C = (-4, 2) and
radius= \(\sqrt{16+4+16}=6\)
CL = Perpendicular distance from C(-4,2) to the chord 3x-y + 4=0.

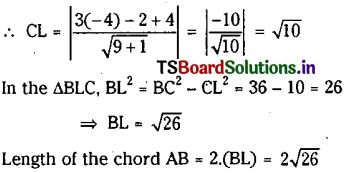
Question 10.
Find the equation of tangents to x²+y²-4x+6y-12=0 which are parallel to x + 2y -8 = 0.
Solution:
Centre of the given circle C = (2, -3) and radius \(\sqrt{4+9+12}\) =5
Any line parallel to x + 2y – 8= 0 is of the form x + 2y + k – 0. If this line becomes a tangent then the perpendicular distance from C(2, -3) to x + 2y + k = 0 is equal to the radius.
∴ \(\left|\frac{2-6+k}{\sqrt{1+4}}\right|=5\)
⇒ |k – 4| = 5\(\sqrt{5}\) ⇒ k = 4 ± 5\(\sqrt{5}\)
∴ Equation of parallel tangents are
x+2y+(4±5\(\sqrt{5}\)  )=0

Question 11.
Find the equation of tangent to x²+y² – 2x+ 4y = 0 at (3, -1). Also find the equation of tangent parallel to it.
Solution:
Equation of tangent at (3, -1) to the circle
x²+y² -3x + = 0 is
x(3)+y(-1)-1(x+3)+2(y-1)=0
= 3x-y-1(x+ 3) + 2(y-1) 0
3x-y-x-3+2y-20
2x+y-5=0 ……………………. (1)
Equational line parallel to 2x + y-5 = 0 is of the from 2x + y + k = 0. If this is a tangent to the given circle then the perpendicular distance from the centre (1, -2) is equal to the radius=\(\sqrt{1+4}=\sqrt{5}\)
∴ \(\left|\frac{2(1)-2+k}{\sqrt{5}}\right|=\sqrt{5}\)
= k -±5
∴ Equations of parallel tangents to (1) are 2x + y ± 5 = 0
∴ The equation of other parallel tangent is 2x + y + 5 = 0

Question 12.
If 4x-3y+7=0 is a tangent to the circle represented by x²+y²-6x+4y-12=0 then find the point of contact.
Solution:
Centre of the given circle C = (3, -2). Let the P(x₁, y₁) be the contact.
Then 4x₁ – 3y₁ + 7 = 0 …………… (1) is perpendicular to PC, equation of PC is 3x + 4y + k = 0
Since this passes through C(3, -2) we have
9 – 8+k=0=k=-1
∴ Equation of CP is 3x₁ + 4y₁ – 1 = 0 ……………. (2)
Solving (1) and (2)

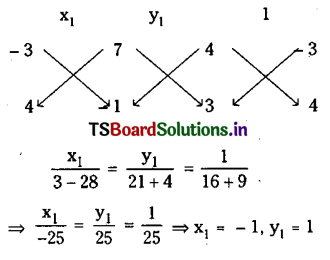
∴ P(-1, 1) is the point of contact.

Question 13.
Find the equations of circles which touch 2x – 3y+ 1 =0 at (1, 1) and having radius \(\sqrt{13}\)
Solution:

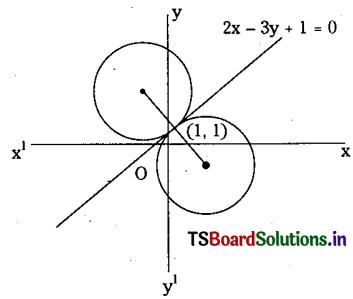
Equation of line ⊥r to 2x – 3y 1 – 0 is of the from 3x + + k -0; Since this passes through
(1, 1) we have 3+2 +k=0 ⇒ k=-5
Equation of line perpendicular to the tangent is 3x+2y-5=0 ………….. (1)
Let (x, y) be the centre of circle

⇒ x² – 2x-3=0 ⇒ (x-3)(x+1)=0
⇒ x = 3 or x = – 1
When x = 3, we have from (1) y =\(\frac{5-9}{2}\) – 2
and when x=-1, y = \(\frac{5+3}{2}=4\)
∴ Centre are (3, -2) and (-1, 4).
∴ Equations of circles with (3, – 2) and
(-1, 4) With radius ,\(\sqrt{13}\) are given by
(x-3)² + (y+ 2)² = 13 and (x+ 1)² + (3,4)² = 13
= x² +y²-6x+4y=0 and x² +y²-2x-8y+4 = 0.

Question 14.
Find the equation of the tangent at the point 300 (Parametric value of O) of the circle x2 4-y2+4x+6y-39=0.
Solution:
Here g=2, f=3. c=-39
\(r=\sqrt{4+9+39}=\sqrt{52}=2 \sqrt{13}\)
The required equation of tangent at ‘θ’ to
S = 0 is given by the formula

Question 15.
Find the equation of normal to the circle x²+y²– 4x-6y+ 11 =0 at (3, 2), Also find the other point where the normal meets the circle.
Solution:
Let A(3, 2) and C be the centre of the given circle C = (2, 3) = (-g,-f)
Equation of normal at (x₁, y₁) is (x-x₁)(y₁+f)-(y-y₁)(x₁+g) = 0
⇒ (x-3)(2-3)-(y-2)(3-2)=0
⇒ 1(x-3)- 1(y-2)= 0
⇒ x-y+5 =0 x+y-5 =0
Let B (x₁, y₁) be the other point where the normal meets the circle.
Then \(\frac{x_1+3}{2}=2\) and \(\frac{y_1+2}{2}=3\)
x₁ = 1, and y₁ = 4
Hence normal at (3,2) meets the circle at (1,4).

Question 16.
Find the area of the triangle formed by the normal at (3, -4) to the circle x²+y²-22x-4y+ 25=0 with the coordinate axes.
Solution:
From the given equation of circle
2g = -22 and 2f = – 4=g=-11 and f=-2
Also (x₁, y₁) =(3,-4)
Then equation of normal al (x₁, y₁) is
(x-x₁)(y-y₁)-(y-y₁)(x₁ +g)=0
⇒ (x-3)(-4-2)-(y+4)(3-11)=0
⇒ (x-3)(-6)-(y+4)(-8)=0
⇒ -6x + + 50 = 0
⇒ 3x – 4y – 25 = 0

Question 17.
If θ₁, θ₂ are the angles of inclination of tangents through a point P to (lie circle x² + y²= a² then find the locus of P where cot θ₁+ cot θ₂ = k
Solution:
The equation of tangent to the circle x² + y² = a² having slope m is y = mx + \(a \sqrt{1+m^2}\)
Let P(x₁, y₁) be a point on the locus. Then

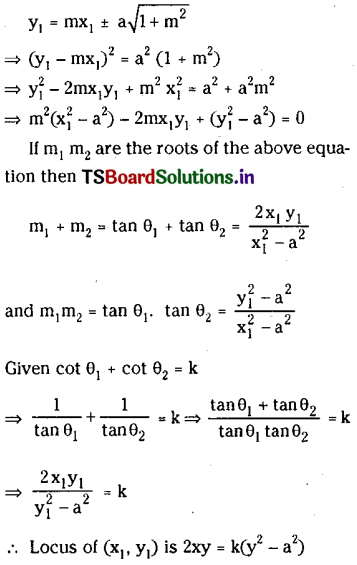
Question 18.
If the chord of contact of P with respect to the circle x² + y² = a² cut the circle at A and B such that \(\angle \mathrm{AOB}=90^{\circ}\) then show that P lies on the circle x²+y²=2a².
Solution:

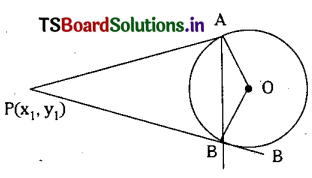
Let P(x₁, y₁) be a point and let the chord of contact of P(x₁, y₁) meets circle are A and B.Such that \(\angle \mathrm{AOB}=90^{\circ}\)
Equation of chord of contact of P(x₁, y₁) is
xx₁ + yy₁ – a₂ = 0 ⇒ \(\frac{x_1+y y_1}{a^2}=1\) ……….. (1)

Question 19.
Show that the poles of tangents to the circle x+y = a² w.r.t. the circle (x + a)² + 2 = 11 on y² + 4ax = 0.
Solution:
Let P(x₁, y₁) be the pole of the tangent to the circle x² + y² – a² …………………… (1) w.r.t circle (x + a)² + y² = 2a². Then the equation of polar of P (x₁, y₁) w.r.t
(x + a)² + y² . 2a² is …………………. (2)
xx₁ +yy₁ +a(x₁+ y₁)-a²= 0
= x(x₁ + a) + yy₁ + (ax₁ – a₂) = 0 ………………. (3)
The line is a tangent to the circle (1) then perpendicular distance from (0, 0) to (3) is equal to radius ‘a’.

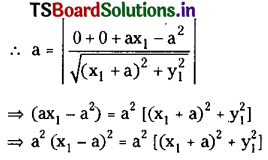
Question 20.
Show that the area of the triangle formed by the two tangents through P(x₁, y₁) to the circle S=x²+y²+2gx+2fy+c=0 and the chord of contact of P.w.r. IS=0 is \(\frac{r\left(S_{11}\right)^{\frac{3}{2}}}{S_{11}+r^2}\)  where r is the radius of the circle.
Solution:

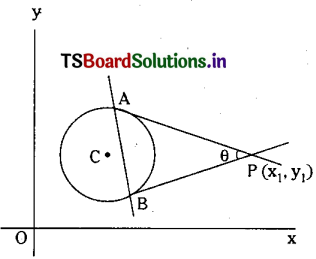
Let PA and PB be the two tangents drawn from P(x), y) to the circle S = 0 and θ be the angle between these two tangents.
Then tan = \(\frac{\theta}{2}=\frac{r}{\sqrt{S_{11}}}\)
Area of triangle formed by the tangents through P(x₁, y₁) to S = 0 and the chord of contact of P w.r.t S = 0

Question 21.
Find the mid point of the chord Intercepted by x²+ y² – 2x – 10y + 1 = 0 on the line x – 2y + 7 = 0.
Solution:
Let x²+ y² – 2x – 10y + 1 = 0 ………………. (1)
x – 2y+ 7= 0 ……………… (2)
Let P(x₁, y₁) be the midpoint of the chord intercepted by the circle (L) on the line given by (2).
The equation of chord of (x₁, y₁) in terms of its midpoint is

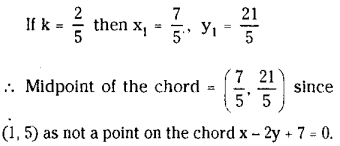
Question 22.
Find the equation of pair of tangents drawn from (10, 4) to the circle x² + y² = 25.
Solution:
Equation of pair of tangents is S. S₁₁ = S₁²
⇒ (100+16-25)(x²+y²-25)=(10x+4y-25)²
⇒ 91(x²+ y²-25)=100x²+16y²+625+80xy – 200y – 500x
⇒ 9x² +80xy-75y²-500x-200y + 2900=0

Long Answer Type Questions

Question 1.
Find the equation of circle passing through P(1, 1), Q(2, -1) and R(3, 2).
Solution:

Question 2.
Find the equation of the circumcircle of the triangle formed by the line ax + by + c=0 (abc ≠ 0) and the coordinate axes.
Solution:
Let the line ax+by+c=0 cuts x, and y axis at A and B so that

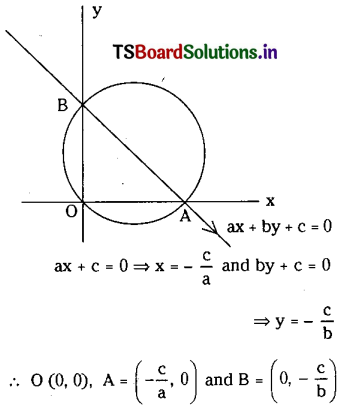
are the vertices of the triangle.
Let x²+y²+2gx+2fy+c=0 …………… (1) be the required equation of the circle. Since it passes through (0, 0) we have c= 0.

Question 3.
Find the locus of mid points of the chords of contant of x² + y² = a² from the points lying on the line lx + my + n=0.
Solution:
Let (x₁, y₁) be the locus of mid points of chords of the circle x² + y² = a² ………………. (1)
and this is a chord lies on ix + my + n = 0 ………………… (2)
i.e., pole of this chord is on (2).
Equation of chord of (1) having (x₁, y₁) as its mid point is xx₁ + yy₁ – x + y

Question 4.
Show that four common tangents can be drawn for the circles given by
x²+y²-14x+6y+33=9 ……………… (1)
x²+y²+30x-2y+1=0………………(2)
and find the Internal and external centres of similitude.
Solution:
Centre of circLe (1) is C₁ = (7, – 3)
Centre of circle (2) is C₂ = (15, 1)

Question 5.
Prove that the circles
x²+y²-8x-6y+21=0 ……………. (1) and x²+y²-2y-15=0 ………………… (2) have exactly two common tangents.
Also find the point of Intersection of those tangents.
Solution:
Centres of circles are C₁ (4, 3) and C₂ – (0, -1)

∴ Given circles intersect each other and have exactly two common tangents.
r₁ : r₂ = 2 : 4 = 1: 2
The point of contact P divides C₁C₂ externally in the ratio 1: 2.
∴ External centre of similitude
= \(\left(\frac{8-0}{2-1}, \frac{6-1}{2-1}\right)=(8,5)\)

Question 6.
Show that the circles
x²+y²– 4x-6y-12=0 ………………. (1)
and x²+y²+6x+18y+26=0 …………….. (2) touch each other. Also find the point of contact and common Langent at this point of contact.
Solution:
Let C₁ (2, 3) and C₂ (- 3, -9) are centres of circles (1) and (2) and their radii are

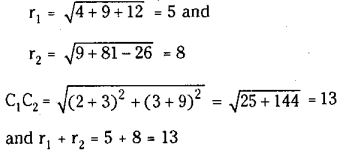
C₁C₂ = r₁ + r₂ and hence the two circles touch each other externally. Point of contact divides C₁C₂ in the ratio
r₁ : r₂ = 5 : 8

Question 7.
Show that the circles x²+y²-4x-6y-12=0 and 5(x²+y²)-8x-14y-32=0 touch each other and find their point of contact.
Solution:

Now \(\overline{\mathrm{C}_1 \mathrm{C}_2}\) = | r₁-r₂ |
Here the circles (1) and (2) touch each other internally the point of contact P dividies C₁C₂ in the ratio 5 : 3 externally.
\(\mathrm{P}=\left(\frac{3(2)-5\left(\frac{4}{5}\right)}{3-5}, \frac{3(3)-5\left(\frac{7}{5}\right)}{3-5}\right)\)
E (-1, – 1)
∴ Point of contact = (-1, -1)

Question 8.
Find the equations to all possible common tangents of the circles
x²+y² -2x-6y+6=0 ………………. (1) and x²+y² = 1 …………………. (2)
Solution:
Centres of circles are C₁ – (1, 3) and C₂ (0, 0)

= 4y + 3xy- 9y – 3x + 5 = 0
= (y +l) (4y + 3x + m) (Suppose)
Equating the coefficient of x, y and constant terms
3l = – 3 ………………. (3)
and 4l + m = – 9 ……………..(4)
lm=5 …………….. (5)
From (3) and (4) l=-1⇒m=-5
Equations of transverse common tangents are (y-1) = 0 and 4y+3x-5=0
Direct common tangents are given by
(x²+y²-1)(1+9-1)=(xi-3y+ 1)²
=9(x²+y²-1)=x²+9y²+1+6xy+6y+2x
8x²– 6xy-2x – 6y- 10=0
= (x+l) (8x-6y+m)
Comparing coefficient of x, y and constant and
8l+m=-2
and -6l=-6 =l= l and
lm = – 10 ⇒ m – 10
Equations of direct common tangents are
x+ 1-0 and 8x-6y-10-0
⇒ 4x – 3y – 5 = 0