TS 10th Class Maths Important Questions Chapter 1 Real Numbers

These TS 10th Class Maths Chapter Wise Important Questions Chapter 1 Real Numbers given here will help you to solve different types of questions.

TS 10th Class Maths Important Questions Chapter 1 Real Numbers

Previous Exams Questions

Question 1.
Insert 4 rational numbers between \(\frac{3}{4}\) and 1 without using \(\frac{a+b}{2}\) formula. (T.S. Mar. ’15)
Solution:
\(\frac{3}{4}\) and 1 = \(\frac{3}{4}\) and \(\frac{4}{4}\)
\(\frac{3}{4}\) = \(\frac{30}{40}\) and \(\frac{4}{4}\) = \(\frac{40}{40}\)
So, in between \(\frac{30}{40}\) and \(\frac{40}{40}\) any 4 rational numbers to be noted.
\(\frac{30}{40}\), \(\frac{31}{40}\), \(\frac{32}{40}\), \(\frac{33}{40}\), \(\frac{34}{40}\) …………… , \(\frac{39}{40}\), \(\frac{40}{40}\)
So from \(\frac{31}{40}\) to \(\frac{39}{40}\) any four we can take.

Question 2.
Write any three numbers of two digits. Find the LCM and HCF for the above numbers by the Prime Factorization method. (T.S. Mar.’15)
Solution:
Take any three two digit numbers. Say 8, 10 and 12.
Prime factorization of these numbers are
8 = 2 × 2 × 2 = 2³
10 = 2 × 5 = 2 × 5
12 = 2 × 2 × 3 = 2² × 3
L.C.M of 8, 10 and 12 is 2 × 2² × 5 × 3 = 120
H.C.F of 8, 10 and 12 = 2

Question 3.
Give an example for each of the following :
i) The product of two irrational numbers is a rational number.
ii) The product of two irrational numbers is an irrational number. (T.S. Mar.’15)
Solution:
i) Let us consider two irrational numbers
\(\sqrt{2}\), \(\sqrt{50}\)
Their product is
= (\(\sqrt{2}\)) (\(\sqrt{50}\)) = \(\sqrt{100}\) = 10
which is a rational number.

ii) Again let us consider two irrational numbers = \(\sqrt{3}\), \(\sqrt{7}\)
Their product = (\(\sqrt{3}\)) (\(\sqrt{7}\)) = \(\sqrt{21}\)
which is an irrational number.

Question 4.
Find the value of \(\log _5^{125}\) (T.S. Mar.’16)
Solution:
We have the rule
if \(\log _a^N\) = x then a^x = N.
Let us consider \(\log _5^{125}\) = x
then 5^x = 125 = 5³
⇒ x = 3. So \(\log _5^{125}\) = 3.

Question 5.
If x² + y² = 7xy then show that 2 log (x + y) = log x + log y + 2 log 3. (T.S. Mar. ’15 )
Solution:
x² + y² = 7xy (given)
Add 2xy in both sides of above equation.
⇒ x² + y² + 2xy = 7xy + 2xy = 9xy
So (x + y)² = 9xy (Consider logarithm on both sides)
We get log (x + y)² = log 9xy
⇒ 21og (x + y) = log 9 + log x + log y
= log x + log y + log 3²
= log x + log y + 2 log 3
∴ 2 log (x + y) = log x + log y + 2 log 3
∴ Hence proved.

Question 6.
Use Eculid’s division lemma to show that the cube of any positive integer is of the form 7 m or 7m + 1 or 7m + 6.
Solution:
From the Euclid’s lemma we can consider a positive integer ‘a’
a = bq + r (r is the remainder)
Let us now consider a positive integer ‘a’ and
b = 7 then ‘a’ is in the form of
a = 7q + r
(r = either 0, 1,2, 3, 4, 5 or 6)
If r = 0 then a = 7q
r = 1 then a = 7q + 1
r = 2 then a = 7q + 2
r = 6 then q = 7q + 6
So ‘a’ will be in the form of anyone of the above
Then abc of the positive integer a is a³
So a = 7q + r
⇒ a² = (7q + r)²
(∵ (a + b)³ = a³ + b³ + 3a²b + 3ab²)
⇒ a³ = 343q³ + 49q²r + 7qr² + r³
= 7 [49q³ + 7q²r + qr²] + r³
= 7m + r³
[where 49q³ + 7q²r + qr² = m ]
a³ = 7m + r³
If r = 0 then a³ = 7m + 0³ = 7m
r = 1 then a³ = 7m + 1³ = 7m + 1
r = 2 then a³ = 7m + 2³
= 7m + 8
= 7 (m + 1) + 1
So it is m the form of 7m + 1
If r = 3 then a³ = 7m + 3³
= 7m + 27
= 7m + 21 + 6
= 7(m + 3) + 6
It is in the form of 7m + 6
If r = 4 then a³ = 7m + 4³
= 7m + 64
= 7m + 63 + 1
= 7(m + 9) + 1
= 7m + 1 form
if r = 5 then a³ = 7m + 5³
= 7m + 125
= 7m + 119 + 6
= 7(m + 17) + 6
= 7m + 6 form
If r = 6 then a³ = 7m + 6³
= 7m + 216
= 7m + 210 + 6
= 7(m + 30) + 6
= 7m + 6 form
So, cube of a positive integer will be either in the form of 7m, 7m, +1 or 7m + 6.

Question 7.
Show that \(\sqrt{2}\) – 3\(\sqrt{5}\) is a irrational number. (T.S. Mar. ’15)
Solution:
Consider \(\sqrt{2}\) – 3\(\sqrt{5}\) is not an irrational one. Then it will be a rational number. That means it will be in the form of \(\frac{\mathrm{p}}{\mathrm{q}}\) (q ≠ 0) (p, q are mutual prime)
∴ \(\sqrt{2}\) – 3\(\sqrt{5}\) = \(\frac{\mathrm{p}}{\mathrm{q}}\)
⇒ \(\sqrt{2}\) = \(\frac{\mathrm{p}}{\mathrm{q}}\) + 3\(\sqrt{5}\)
(squaring on both sides)

Since p and q are integers the RHS part of above equation (1) becomes a rational and RHS part \(\sqrt{5}\) is an irrational one which is unfair.
So our assumption is wrong.
Then \(\sqrt{2}\) – 3\(\sqrt{5}\) is an irrational number.

Additional Questions

Question 1.
Use Euclid’s division algorithm to find the HCF of
(i) 500 and 150
(ii) 194 and 35890
(iii) 1550 and 3150
Solution:
Theorem : Euclid’s Division Lemma a = bq + r, q > 0 and 0 < r < b
(i) 500 and 150
When 500 is divided by 150, then the remainder is 50 to get
500 = 150 × 3 + 50
Now consider division of 150 with the remainder 50 in the above and division algorithm to get
150 = 50 × 3 + 0
Then the remainder is zero. When we can not proceed further, we conclude that the
HCF of (500, 150) = 50

(ii) 194 and 35890
When 35890 is divided by 194, the remainder is zero to get
35890 = 194 × 185 + 0
The remainder is zero. When we can not proceed further, we conclude that the
HCF of (35890, 194) = 194

(iii) 1550 and 3150
When 1550 is divided by 3150 then the remainder is 50 to get
3150 = 1550 × 2 + 50
Now consider the division of 150 with the remainder 50 in the above and division algorithm to get
1550 = 50 × 31 + 0
The remainder is zero. When we can not proceed further we conclude that the
HCF of 3150, 1550 = 50

Question 2.
Use Euclid division Lemma to show that any positive even integer is of the form 4q or 4q + 2 or 4q + 4 when q is some integer.
Solution:
Let ‘a’ be any positive even integer. We apply the division algorithm with a and b = 4 since 0 ≤ r < 4, the possible remainder are 0, 1, 2, 3 and 4 (∵ a = bq + r)
i.e., a can be 4q or 4q + 1 or 4q + 2 or 4q + 3 or 4q + 4 where q is the quotient.
However since a is even, a cannot be 4q + 1 and 4q + 3 (∵ They are not divisible by 2)
∴ Any positive even integer in the form of 4q or 4q + 2 or 4q + 4.

Question 3.
Use Euclid division Lemma to show that any positive odd integer is of the form 2q + 1, 2q + 3 or 2q +5 when q is some integer.
Solution:
Let ‘a’ be any positive odd integer. We apply the division algorithm with a and b = 2
Since 0 ≤ r < 5, the possible remainders are
0, 1, 2, 3, 4 and 5 i.e., a can be 2q or 2q + 1 or 2q + 2 or 2q + 3 or 2q + 4 or 2q + 5 when q is the quotient.
However since ‘a’ is odd ‘a’ cannot be 2q or 2q + 2 or 2q + 4 (∵ They are divisible by 2)
Any odd integer is of the form 2q + 1 or 2q + 3 or 2q + 5

Question 4.
Use Euclid division Lemma to show that any positive even integer is of the form. 2q or 2q + 2 or 2q + 4 where q is some integer.
Solution:
Let a be and positive even integer. We apply the division algorithm with a and b = 2. Since 0 ≤ r < 4, the possible remainders are 0, 1,2, 3 and 4 (∵ a = bq + r)
1. e., a can be 2q or 2q + 1 or 2q + 2 or 2q + 3 or 2q + 4 where q is the quotient.
However, since a is even, a cannot be 2q + 1 and 2q + 3 (They are not divisible by 2)
∵ Any positive even integer is of the form 2q or 2q + 2 or 2q + 4

Question 5.
Express each number as a product of its prime factors.
(i) 540
(ii) 882
(iii) 1764
(iv) 1080
(v) 6292
Solution:
(i) 540 = 2 × 270
= 2 × 2 × 135
= 2² × 5 × 27
= 2² × 5 × 3 × 9
= 2² × 5 × 3 × 3²
= 2² × 5 × 3³

(ii) 882 = 2 × 441
= 2 × 3 × 147
= 2× 3 × 3 × 49
= 2 × 3² × 7 × 7
= 2 × 3² × 7²

iii) 1764 = 2 × 882
= 2 × 2 × 441
= 2² × 3 × 147
= 2² × 3 × 3 × 49
= 2² × 3² × 7²

iv) 1080 = 2 × 540
= 2 × 2 × 270
= 2² × 2 × 135
= 2³ × 5 × 27

v) 6292 = 2 × 3146
= 2 × 2 × 1573
= 2² × 11 × 143
= 2³ × 11 × 11 × 13
= 2² × 11² × 13

Question 6.
Find the LCM and HCF of the following integers by the prime factorisation method.
(i) 10, 15 and 35
(ii) 13, 17 and 23
(iii) 7, 9 and 25
(iv) 84 and 108
(v) 234 and 747
Solution:
HCF : Product of the smallest power of each common prime factors in the numbers.
LCM : Product of the greatest power of each prime factor in the numbers.

(i) 10, 15 and 35
10 = 5 × 2
15 = 5 × 3
35 = 5 × 7
HCF = 5,
LCM = 2 × 3 × 5 × 7
= 210

(ii) 13, 17 and 23
13 = 1 × 13
17 = 1 × 17
23 = 1 × 23
HCF = 1, LCM = 13 × 17 × 23 = 5083

(iii) 7, 9 and 25
7 = 1×7
9 = 1 × 3 × 3 = 1 × 3²
25 = 1 × 5 × 5 = 1 × 5²
HCF = 1, LCM = 7 × 3² × 5²
= 7 × 9 × 25 = 1575

(iv) 84 and 108
84 = 2 × 42 = 2 × 2 × 21 = 2² × 3 × 7
108 = 2 × 54 = 2 × 2 × 27 = 2² × 3³
HCF = 2² × 3 = 4 × 3 = 12
LCM = 2² × 3³ × 7 = 756

(v) 234 and 747
234 = 2 × 117 = 2 × 3 × 39 = 2 × 3 × 3 × 13
= 2 × 3² × 13
747 = 3 × 249
= 3 × 3 × 83
= 3² × 83
HCF = 3² = 9
LCM = 2 × 3² × 13 × 83 = 19422

Question 7.
Explain why 5 × 11 × 12 + 12 is a composite number.
Solution:
Note : Every composite number can be expressed as a product of primes.
Given numbers is 5 × 11 × 12 + 12
= 12(5 × 11 + 1)
= 12(55 + 1)
= 12 (56)
= 12 × 2 × 28
= 4 × 3 × 2 × 4 × 7
= 2² × 3 × 2 × 2² × 7
= 2⁵ × 3 × 7
= Product of prime factors Hence the given number is a composite number.

Question 8.
How will you show that 41 × 17 × 61 × 3 + 41 × 17 × 31 × 5 is a composite number ? Explain.
Solution:
Given number is 41 × 17 × 61 × 3 + 41 × 17 × 31 × 5
= 41 × 17 (61 × 3 + 31 × 5)
= 41 × 17(183 + 155)
= 41 × 17 (338)
= 41 × 17 × 2 × 169
= Product of prime factors
Since given number is a product of primes
∴ Given number is a composite number.

Question 9.
Expenses each member as a product of its prime factors.
(i) 504
(ii) 756
(iii) 1800
(iv) 8228
(v) 6084
Solution:
(i) 504
= 2 × 252
= 2 × 2 × 126
= 2² × 2 × 63
= 2³ × 9 × 7
= 2³ × 3² × 7

(ii) 756
= 2 × 378
= 2 × 2 × 189
= 2² × 3 × 63 ⇒ 2² × 3 × 3 × 21
= 2² × 3² × 3 × 7
= 2² × 3³ × 7

(iii) 1800
= 2 × 900
= 2 × 2 × 450
= 2² × 2 × 225
= 2³ × 3 × 75 ⇒ 2³ × 3 × 3 × 25
= 2³ × 3² × 5²

(iv) 8228
= 2 × 4114
= 2 × 2 × 2057
= 2² × 11 × 187
= 2² × 11 × 11 × 17
= 2² × 11² × 17

(v) 6084
= 2 × 3042
= 2 × 2 × 1521
= 2² × 3 × 507
= 2² × 3 × 3 × 169
= 2² × 3² × 13 × 13
= 2² × 3² × 132

Question 10.
Explain why 31 × 17 × 13 × 12 + 31 × 17 × 5 a composite number.
(Note : Every composite number can be expressed as a product of primes.
Solution:
Given number is 31 × 17 × 13 × 12 + 31 × 17 × 5
= 31 × 17(13 × 12 + 5)
= 31 × 17 (156 + 5)
= 31 × 17(161)
= 31 × 17 × 7 × 23
= Product of prime factors
Since given number is a product of primes.
∴ Given number is a composite number.

Question 11.
Write the following rational numbers in their decimal form and also state which are terminating and which have non-terminating, a repeating decimal.
(i) \(\frac{5}{8}\)
(ii) \(\frac{17}{200}\)
(iii) \(\frac{21}{125}\)
(iv) \(\frac{7}{11}\)
Solution:
(i) \(\frac{5}{8}\) = \(\frac{5}{2.2 .2}\) = \(\frac{5}{2^3}\) is a terminating decimal.
∵ Denominator consists of only 2’s
= \(\frac{5 \times 5^3}{2^3 \times 5^3}\) = \(\frac{5 \times 125}{10^3}\) = \(\frac{625}{1000}\)
= 0.625

(ii) \(\frac{17}{200}\) = \(\frac{17}{2.2 .2 .5 .5}\) = \(\frac{17}{2^3 \times 5^2}\) is a terminating decimal
∵ Denominator consists of only 2’s and 5’s

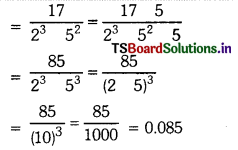
(iii) \(\frac{21}{125}\) = \(\frac{21}{5^3}\) is a terminating decimal
∵ Denominator consists of only 5’s

(iv) \(\frac{7}{11}\) is a non-terminating, repeating 2’s or 5’s or both
∵ Denominator doesn’t contain 2’s and 5’s or both ‘
\(\frac{7}{11}\) = 0.636363

Question 12.
Without actually performing division. State whether the following rational numbers will have a terminating decimal form or a non – terminating, repeating decimal form.
(i) \(\frac{14}{625}\)
(ii) \(\frac{13}{12}\)
(iii) \(\frac{74}{455}\)
(iv) \(\frac{76}{200}\)
Solution:
(i) \(\frac{14}{625}\) : It is the form of \(\frac{\mathrm{P}}{\mathrm{q}}\) .
\(\frac{14}{625}\) = \(\frac{14}{5.5 .5 .5}\) = \(\frac{14}{5^4}\)
∵ q = 5⁴ which is of the form 2ⁿ.5^m (n = 0, m = 4)
∴ Given rational number has a terminating decimal expansion.

(ii) \(\frac{13}{12}\) : It is of the form \(\frac{\mathrm{P}}{\mathrm{q}}\).
\(\frac{13}{12}\) = \(\frac{13}{2 \times 2 \times 3}\) = \(\frac{13}{2^2 \times 3}\) = 1 083333
∴ q = 2² × 3 which is not of the form 2ⁿ × 5^m
∴ Given rational number has a non-terminating repeating decimal expansion.

(iii) \(\frac{74}{455}\) : It is the form of \(\frac{\mathrm{P}}{\mathrm{q}}\).
\(\frac{74}{455}\) = \(\frac{74}{5 \times 7 \times 13}\)
∴ q = 5 × 7 × 13 which is not in the form 2ⁿ . 5^m
∴ Given rational number has a non terminating repeating decimal expansion.

(iv) \(\frac{76}{200}\) : It is of the form \(\frac{\mathrm{P}}{\mathrm{q}}\).
\(\frac{76}{200}\) = \(\frac{76}{2^3 \times 5^2}\)
∴ q = 2³ × 5² which is of the form 2ⁿ . 5^m (n = 3, m = 2)
∴ Given number has a terminating decimal expansion.

Question 13.
Write the decimal expansion of the following :
(i) \(\frac{27}{25}\)
(ii) \(\frac{35}{32}\)
(iii) \(\frac{43}{2^3 \cdot 5^2}\)
(iv) \(\frac{729}{3^2 \cdot 5^2}\)
Solution:
Hint: Convert the denominator into the form 10ⁿ or 2ⁿ.5^m.

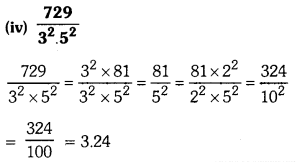
Question 14.
Write the decimal expansion of the following.
(i) \(\frac{17}{25}\)
(ii) \(\frac{35}{16}\)
(iii) \(\frac{33}{2^3 \cdot 5^2}\)
(iv) \(\frac{243}{3^2 \cdot 5^2}\)
Solution:
Hint : Convert the denominator into the form 10ⁿ or 2ⁿ.5^m.

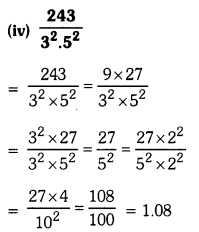
Question 15.
Prove the following are irrational.
(i) \(\sqrt{2}\) + \(\sqrt{5}\)
(ii) \(\sqrt{7}\)
(iii) 7 + \(\sqrt{3}\)
(iv) 6 – \(\sqrt{2}\)
Solution:
(i) \(\sqrt{2}\) + \(\sqrt{5}\)
Let us assume to the contrary that \(\sqrt{2}\) + \(\sqrt{5}\) is a rational number.
Then, there exist co-prime positive integers ‘a’ and ‘b’ such that

\(\frac{a^2-3 b^2}{2 a b}\) = \(\sqrt{2}\)
But \(\sqrt{2}\) is a rational number.
i.e., \(\frac{a^2-3 b^2}{2 a b}\) is rational.
This contracts the fact that \(\sqrt{2}\) is irrational.
So our assumption is wrong.
∴ Hence \(\sqrt{2}\) + \(\sqrt{5}\) is irrational.

(ii) \(\sqrt{7}\)
Let us assume, to the contrary, that \(\sqrt{5}\) is rational. Then there exist co-prime positive integer a and b such that
\(\sqrt{7}\) = \(\frac{a}{b}\)
\(\sqrt{7}\) b = a
SB.S., we get
7b² = a² …………….. (1)
7 divides a²
Hence 7 divides a
We can write a = 7c for same integer ‘c’. Substitute a = 7c in (1), we get
7b² = (7c)²
b² = \(\frac{49 c^2}{7}\) 7c²
7 divides b² and 7 divide b
‘a’ and ‘b’ have atleast as a common factor. This contradicts the fact that ‘a’ and ‘b’ have no common factor other than 1.
So our assumption is wrong.
∴ \(\sqrt{7}\) is irrational.

(iii) 7 + \(\sqrt{3}\)
Let us assume on the contrary that 7 + \(\sqrt{3}\) = is a rational. Then there exist co-prime positive integers ‘a’ and ‘b’ such that 7 + \(\sqrt{3}\) = \(\frac{a}{b}\)
\(\sqrt{3}\) = \(\frac{a}{b}\) – 7
⇒ \(\sqrt{3}\) = \(\frac{a-7 b}{b}\)
∴ \(\sqrt{3}\) is rational ⇒ \(\frac{a-7 b}{b}\) is rational.
This contradicts the fact that \(\sqrt{3}\) is irrational, so our assumption is wrong
∴ 7 + \(\sqrt{3}\) is irrational.

(iv) 6 – \(\sqrt{2}\)
Let us assume on the contrary that 6 – \(\sqrt{2}\) is rational. Then there exist co-prime positive in-tegers ‘a’ and ‘b’ such that
6 – \(\sqrt{2}\) = \(\frac{a}{b}\)
⇒ 6 – \(\frac{a}{b}\) = \(\sqrt{2}\)
⇒ \(\frac{6 b-a}{b}\) = \(\sqrt{2}\)
\(\sqrt{2}\) is rational \(\frac{6 b-a}{b}\) is rational. This contradicts the fact that \(\sqrt{2}\) is irrational. So our assumption is wrong.
∴ 6 – \(\sqrt{2}\) is irrational.

Question 16.
Prove that \(\sqrt{\mathrm{p}}\) – \(\sqrt{\mathrm{q}}\) is irrational when p, q are primes.
Solution:
Let us assume to the contrary that \(\sqrt{\mathrm{p}}\) – \(\sqrt{\mathrm{q}}\) is rational. Then exist co-prime positive integers ‘a’ and ‘b’

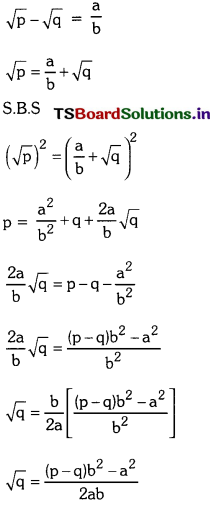
We know that square root of any prime number in irrational. We get \(\sqrt{\mathrm{q}}\) is a rational.
This contradicts the fact that \(\sqrt{\mathrm{q}}\) is irrational. So, our assumption is wrong.
∴ \(\sqrt{\mathrm{q}}\) is irrational
∴ Hence \(\sqrt{\mathrm{p}}\) – \(\sqrt{\mathrm{q}}\) is irrational.

Question 17.
Prove that the following are irrational
(i) \(\sqrt{5}\) + \(\sqrt{3}\)
(ii) \(\sqrt{3}\)
(iii) 7 + \(\sqrt{2}\)
Solution:
(i) \(\sqrt{5}\) + \(\sqrt{3}\)
Let us assume to the contrary that \(\sqrt{5}\) + \(\sqrt{3}\) is a rational number.
Then exist co-prime positive integers ‘a’ and ‘b’ such that
\(\sqrt{5}\) + \(\sqrt{3}\) = \(\frac{a}{b}\)

This contradicts the fact that \(\sqrt{3}\) is irrational. So our assumption is wrong.
∴ Hence \(\sqrt{5}\) + \(\sqrt{3}\) is irrational.

(ii) \(\sqrt{3}\)
Let us assume to the contrary, that \(\sqrt{3}\) is rational. Then there exist co-prime positive integers a and b such that
\(\sqrt{3}\) = \(\frac{a}{b}\)
\(\sqrt{3}\)b = a
S.B.S. We get
3b² = a² ………………. (1)
3 divides a²
We can write a = 3c for same integer c substitute a = 3c in (1), we get
3b² = (3c)²
b² = \(\frac{9 c^2}{3}\) = 3c²
3 divides b² and 3 divide b.
‘a’ and ‘b’ have atleast as a common factor. This contradicts the fact that ‘a’ and ‘b’ have no common factor other than 1.
So, our assumption is wrong.
∴ \(\sqrt{3}\) is irrational.

(iii) 7 + \(\sqrt{2}\)
Let us assume on the contrary that 7 + \(\sqrt{2}\) is a rational. Then there exist co-prime positive integers ‘a’ and ‘b’ such that
7 + \(\sqrt{2}\) = \(\frac{a}{b}\)
\(\sqrt{2}\) = \(\frac{a}{b}\) – 7
\(\sqrt{2}\) = \(\frac{a-7 b}{b}\)
\(\sqrt{2}\) is rational ⇒ \(\frac{a-7 b}{b}\) is rational.
This contradicts the fact that \(\sqrt{2}\) is irrational. So our assumption is wrong.
∴ 7 + \(\sqrt{2}\) is irrational

Question 18.
Determine the value of the following.

Solution:

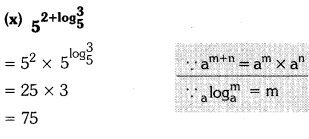
Question 19.
Write each of the following expressions! as log N. Determine the value of N. (Take the base as 10).
(i) log 2 + log 50
(ii) log 50 – log 2
(iii) 4 log 3
(iv) 3 log 2 – 2 log 3
(v) log 343 + log 1
(vi) 3 log 2 + 2 log 5 – 4 log 2
Solution:
(i) log 2 + log 50
∵ log x + log y = log xy
log 2 + log 50 = log (2 × 50)
= log 100
= \(\log _{10}^{10^2}\) = 2 . \(\log _{10}^{10}\)
= 2 × 1 = 2
∵ log a^m = m log a and \(\log _a^a\) = 1

(ii) log 50 – log 2
∵ log x – log y = log \(\left(\frac{x}{y}\right)\)
log 50 – log 2 = log\(\left(\frac{50}{2}\right)\) = log 25

(iii) 4 log 3
(∵ m log a = log a^m)
4 log 3 = log 3⁴ = log 81

(iv) 3 log 2 – 2 log 3
3 log 2 – 2 log 3 (∵ m log a = log a^m)
⇒ log 2³ – log 3²
∵ log x – log y = log \(\left(\frac{x}{y}\right)\)
= log 8 – log 9 = log \(\left(\frac{8}{9}\right)\)

(v) log 343 + log 1
log 343 + log 1
∵ log x + log y = log (xy)
= log (343 × 1) = log 343

(vi) 3 log 2 + 2 log 5 – 4 log 2
3 log 2 + 2 log 5 – 4 log 2
∵ m log a = log a^m
= log 2³ + log 5² – log 2⁴
= log 8 + log 25 – log 16
= log \(\left(\frac{8 \times 25}{16}\right)\) = log \(\left(\frac{25}{2}\right)\)

Question 20.
Evaluate each of the following in terms of x and y, if it is given x = \(\log _2^3\) and \(\log _2^5\).
(i) \(\log _2^75\)
(ii) \(\log _2^4.5\)
(iii) \(\log _2^90\)
Solution:

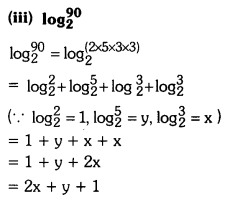
Question 21.
Expand the following.
(i) Log 10000
(ii) log \(\left(\frac{243}{625}\right)\)
(iii) log (x³y²z⁵)
(iv) log \(\left(\frac{p^3 \mathrm{q}^4}{r}\right)\)
(v) log \(\sqrt{\frac{x^5}{y^3}}\)
Solution:
(i) Log 10000
log (10000) = log (2⁴ × 5⁴)
∵ log(xy) = log x + log y
∵ log a^m = m log a
= log2⁴ + log5⁴
= 4 log 2 + 4 log 5
= 4(log 2 + log 5)

(ii) \(\left(\frac{243}{625}\right)\)
log 243 – log 625
= log3⁵ – log5⁴
= 5 log3 – 4 log5

(iii) log (x³y²z⁵)
= log (x³y²z⁵)
= log x³ + log y² + log z⁵
= 3 log x + 2 log y + 5 log z

(iv) log \(\left(\frac{p^3 \mathrm{q}^4}{r}\right)\)
log \(\left(\frac{p^3 \mathrm{q}^4}{r}\right)\) = log p³ + log q⁴ – log r
log p³ + log q⁴ – log r
= 3 log p + 4 log q – log r

(v) log \(\sqrt{\frac{x^5}{y^3}}\)
log \(\sqrt{\frac{x^5}{y^3}}\) = log \(\left(\frac{x^5}{y^3}\right)^{\frac{1}{2}}\)
= \(\frac{1}{2}\) log \(\left(\frac{x^5}{y^3}\right)\)
= \(\frac{1}{2}\) [log(x⁵) – log(y³)]
= \(\frac{1}{2}\) [5 log x – 3 log y]

Question 22.
Determine the value of the following

Solution:
(i) \(\log _{64}^4\)
Let \(\log _{64}^4\) = x
∵ \(\log _a^N\) = x
⇒ N = a^x
4 = (64)^x
4 = (4³)^x ⇒ 4 = 4^3x
⇒ 4^3x = 4¹ ⇒ 3x = 1 ⇒ x = \(\frac{1}{3}\)

(ii) \(\log _{216}^6\)
Let \(\log _{216}^6\) = x
∵ \(\log _a^N\) = x
⇒ N = a^x
6 = (216)^x
⇒ (216)^x = 6 ⇒ (6³)^x = 6¹
⇒ 6^3x = 6¹ ⇒ 3x = 1 ⇒ x = \(\frac{1}{3}\)

(vii) \(\log _{10}^{0.0001}\)
Let \(\log _{10}^{0.0001}\) = x
0.0001 = 10^x ⇒ 10^x = 0.0001
= \(\frac{1}{10000}\) = \(\frac{1}{10^4}\)
10^x = 10^-4 ⇒ x = -4

(viii) \(3^{2+\log _3^7}\)
= \(3^{2+\log _3^7}\)
∵ a^{m + n} = a^m × aⁿ
= 3ⁿ × 3 \(\log _3^7\) (∵\(a^{\log _a^m}\) = m)
= 9 × 7 = 63

Question 23.
Write each of the following expressions as below. Determine the value of N. (Take the base as 10)
(i) log 4 + log 25
(ii) log 100 – log 2
(iii) 3 log 5
(iv) 2 log 4 – 3 log 2
(v) log 625 + log 1
(vi) 2 log 3 + 3 log 4 – 2 log 5
Solution:
(i) log 4 + log 25
log 4 + log 25 (∵ log x + log y = log xy)
= log (4 × 25)
= log 100 = \(\log _{10}^{10^2}\) = 2.\(\log _{10}^{10}\) = 2 × 1 = 2
(∵ log a^m = m log a and \(\log _{a}^{a}\) = 1)

(ii) log 100 – log 2
log 100 – log 2 (∵ log x – log y = log \(\left(\frac{x}{y}\right)\))
= log \(\left(\frac{100}{2}\right)\) = log 50

(iii) 3 log 5
(∵ m log x = log a^m)
3 log 5 = log 5³ = log 125

(iv) 2 log 4 – 3 log 2
(∵ m log a = log a^m)
2 log 4 – 3 log 2 = log 4² – log 2³
= log 16 – log 8
(∵ log x – log y = log \(\left(\frac{x}{y}\right)\))
= log latex]\left(\frac{16}{8}\right)[/latex] = log 2

(v) log 625 + log 1
(∵ log x + log y = log xy)
= log (625 × 1)
= log 625

(vi) 2 log 3 + 3 log 4 – 2 log 5
(∵ m log a = log a^m)
= log 3² + log 4³ – log 5²
= log 9 + log 64 – log 25
= log \(\left(\frac{9 \times 64}{25}\right)\) = log \(\left(\frac{576}{25}\right)\)

Question 24.
Find the value of Log₁₀ 0.001
Solution:
Let Log₁₀ 0.001 = x
10^x = o.001 = \(\frac{1}{1000}\)
10^x = \(\frac{1}{10^3}\) = 10^-3
10^x = 10^-3 ⇒ x = -3

Question 25.
Find the LCM and HCF of the following integers by the prime factorization method. 72 and 108
Solution:
72 and 108
72 = 2 × 36 = 2 × 2 × 18 = 2² × 2 × 9
= 2³ × 3²
108 = 2 × 54 = 2 × 2 × 27 = 2² × 2³
L.C.M = 2³ × 2³ = 8 × 27 = 216
H.C.F. = 2² × 3² = 4 × 9 = 36

Question 26.
Write 2log3 + 3log5 – 5log 2 as single logarithm.
Solution:
2log 3 + 3log 5 – 5log 2 (∵ mloga = loga^m)
= log 3² + log 5³ log 2⁵
= log 9 + log 125 – log 32 [∵ log x + log y = log(xy)]
= log \(\left(\frac{9 \quad 125}{32}\right)\) = log \(\left(\frac{1125}{32}\right)\)
(∵ log x – log y = log \(\left(\frac{x}{y}\right)\))

Question 27.
Prove that the \(\frac{1}{\sqrt{3}}\) is irrational.
Solution:
Let us consider \(\frac{1}{\sqrt{3}}\) is a rational number.
Then take \(\frac{1}{\sqrt{3}}\) = \(\frac{\mathrm{p}}{\mathrm{q}}\) form (where p, q are integers)
⇒ \(\frac{\mathrm{p}}{\mathrm{q}}\) = \(\sqrt{3}\)
i.e. \(\sqrt{3}\) is a rational number and it is a \(\frac{1}{\sqrt{3}}\) contradiction Hence is an irrational number.

Question 28.
Prove that the 3 + 2\(\sqrt{5}\) is irrational
Solution:
Let us assume that 3 + 2\(\sqrt{5}\) is a rational number
3 + 2\(\sqrt{5}\) = \(\frac{\mathrm{p}}{\mathrm{q}}\) (q ≠ 0)
2\(\sqrt{5}\) = \(\frac{\mathrm{p}}{\mathrm{q}}\) – 3 = \(\frac{\mathrm{p – 3q}}{\mathrm{q}}\)
\(\sqrt{5}\) = \(\frac{p-3 q}{2 q}\)
Here p, q being intergers we can say that \(\frac{p-3 q}{2 q}\) is a rational number.
This contradicts that fact that \(\sqrt{5}\) is an irrational number.
Hence our assumption is wrong.
∴ 3 + 2\(\sqrt{5}\) is an irrational number.

Question 29.
Determine the value of

Solution:

∵ \(\log _a^N\) = x
⇒ N = a^x
⇒ \(\left(\frac{3}{5}\right)^x\) = \(\frac{243}{3125}\) = \(\left(\frac{3}{5}\right)^x\)
∵ Bases are equal
∵Powers are equal
x = 5

Question 30.
Solve 7^x = 9^x-2
Solution:
Given 7^x = 9^x-2
Taking log an both sides
log 7^x = log 9^x-2
⇒ x log 7 = (x – 2) log 9
x log 7 = x log 9 – 2 log 9
⇒ 2 log 9 = x log 9 – x log 7
2 log 9 = x (log 9 – log 7)
∴ x = \(\frac{2 \log 9}{\log 9-\log 7}\)

Question 31.
Establish the relation among the sets of Real Numbers, Rational, Irrational, Integers, whole numbers and Natural Numbers using Venn diagrams.
Solution:

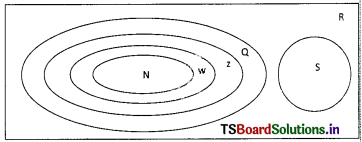
N = the set of natural number
W = the set of whole number
Z = the set of integers
Q = the set of rational number
S = the set of irrational number
R = the set of real number

Question 32.
Prove that 2\(\sqrt{5}\) + \(\sqrt{7}\) is an Irrational Number. Also check whether (2\(\sqrt{5}\) + \(\sqrt{7}\)) (2\(\sqrt{5}\) – \(\sqrt{7}\)) is rational or Irrational.
Solution:
Let us consider 2\(\sqrt{5}\) + \(\sqrt{7}\) be a rational number.
Then 2\(\sqrt{5}\) + \(\sqrt{7}\) = \(\frac{p}{q}\)
Squaring on both sides, we get

LHS is an irrational number.
RHS = p, q being integers, \(\frac{p^2-69 q^2}{4 q^2}\) is a rational number.
This is a contradiction to the fact that \(\sqrt{35}\) is an irrational. Hence our assumption is wrong, and 2 \(\sqrt{5}\) + \(\sqrt{7}\) is an irrational number.
Also
(2\(\sqrt{5}\) + \(\sqrt{7}\)) (2\(\sqrt{5}\) – \(\sqrt{7}\)) = (2\(\sqrt{5}\))² – (\(\sqrt{5}\))²
= 20 – 7
= 13, a rational number