Students can practice TS Class 10 Maths Solutions Chapter 6 Progressions Ex 6.3 to get the best methods of solving problems.
TS 10th Class Maths Solutions Chapter 6 Progressions Exercise 6.3
Question 1.
Find the sum of the following APs :
i) 2, 7, 12, ………., to 10 terms.
Solution:
Given A.P. : 2, 7, 12, ……… to 10 term
a = 2; d = a2 – a1 = 7 – 2 = 5; n = 10
sn = \(\frac{\mathrm{n}}{2}\)[2a + (n – 1)d]
s10 = – \(\frac{10}{2}\)[2 × 2 +(10 – 1)5]
= 5[4 + 9 × 5]
= 5 [4 + 45]
= 5 × 49 = 245
ii) – 37, – 33, – 29, …… to 12 terms.
Solution:
Given A.P :
– 37, – 33, – 29, …., to 12 terms
a = – 37; d = a2 – a1 = (- 33) – (- 37)
= – 33 + 37 = 4 and n = 12
Sn = \(\frac{n}{2}\)[2a+ (n – 1)d]
s12 = \(\frac{12}{2}\)[2 × (-37) + (12 – 1)4]
= 6[-74 + 11 × 4]
= 6[-74 + 44] = 6 × (- 30) = -180
iii) 0.6, 1.7, 2.8, …, to 100 terms.
Solution:
Given A.P : 0.6, 1.7, 2.8, …., S100
a = 0.6; d = a2 – a1 = 1.7 – 0.6 = 1.1 and n = 100
s = \(\frac{\mathrm{n}}{2}\)[2a + (n – 1)d]
s100 = \(\frac{100}{2}\)[2 × 0.6 + (100 – 1) × 1.1]
= 50[1.2 + 99 × 1.1]
= 50[1.2 + 108.9]
= 50 × 110.1 = 5505.
iv) \(\frac{1}{15}\), \(\frac{1}{12}\), \(\frac{1}{10}\) ….. to 11 terms.
Solution:
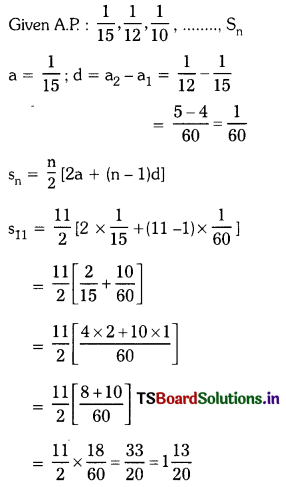
![]()
Question 2.
Find the sums given below :
i) 7 + 10\(\frac{1}{2}\) + 14 + ….. + 84
Solution:
Given A.P. : 7 + 10\(\frac{1}{2}\) + 14 + …… + 84
∴ a = 7, d = a2 – a1 = 10\(\frac{1}{2}\) – 7 = 3\(\frac{1}{2}\)
and the last term l = an
But, an = a +(n – 1) d
∴ 84 = 7 + (n – 1) × 3\(\frac{1}{2}\)
⇒ 84 – 7 = (n – 1) × \(\frac{7}{2}\)
⇒ n – 1 = 77 × \(\frac{2}{7}\) = 22
⇒ n = 22 + 1 = 23
Now, Sn = \(\frac{\mathrm{n}}{2}\)(a + l)
Where a = 7; l = 84
S23 = \(\frac{23}{2}\)(7 + 84)
= \(\frac{23}{2}\) × 91 = \(\frac{2093}{2}\) = 1046\(\frac{1}{2}\)
ii) 34 + 32 + 30 + ……. + 10
Solution:
Given A.P : 34 + 32 + 30 + …….. + 10
Here a = 34; d = a2 – a1 = 32 – 34 = -2
and the last term ‘l‘ = an = 10
But, an = a + (n – 1) d
⇒ 10 = 34 + (n – 1)(-2)
⇒ 10 – 34 = -2n + 2
⇒ -2n = -24 – 2
⇒ n = \(\frac{-26}{-2}\) ∴ n = 13
Also, Sn = \(\frac{\mathrm{n}}{2}\)(a + l)
Where a = 34, l = 10
S13 = \(\frac{13}{2}\)(34 + 10)
\(\frac{13}{2}\) × 44 = 13 × 22 = 286
iii) -5 + (-8) + (-11) + …. + (-230).
Solution:
Given AP:
-5 + (-8) + (-11) + …….. + (-230)
Here first term, a = -5;
Last term, l = an = -230:
d = a2 – a1 = (-8) – (-5)
= -8 + 5 = -3
But, an = a + (n – 1) d
∴ (-230) = (-5) + (n – 1) × (-3)
⇒ -230 + 5 = -3n + 3
⇒ -3n + 3 = -225
⇒ -3n = -225 – 3 ⇒ 3n = 228
∴ n = \(\frac{228}{3}\) = 76
Now Sn = \(\frac{\mathrm{n}}{2}\)(a + l)
S76 = \(\frac{76}{2}\)[(-5) + (-230)]
= 38 × (-235) = -8930
Question 3.
In an AP:
i) Given a = 5, d = 3, an = 50, find n and Sn.
Solution:
Given:
a = 5; d = 3 ; an = a + (n – 1)d = 50
⇒ 50 = 5 + (n – 1)3
⇒ 50 – 5 = 3n – 3
⇒ 3n = 45 + 3
⇒ n = \(\frac{48}{3}\) = 16
Sn = \(\frac{\mathrm{n}}{2}\)(a + l)
S16 = \(\frac{16}{2}\)[5 + 50] = 8 × 55 = 440.
ii) Given a = 7, a13 = 35, find d and S13.
Solution:
Given : a = 7
a13 = a + 12d = 35
⇒ 7 + 12d = 35
⇒ 12d = 35 – 7
⇒ d = \(\frac{28}{12}\) = \(\frac{7}{3}\)
Now, Sn = \(\frac{\mathrm{n}}{2}\)(a + l)
S13 = \(\frac{13}{2}\)[7 + 35]
= \(\frac{13}{2}\) × 42 = 13 × 21 = 273
iii) Given a12 = 37, d = 3, find a and S12.
Solution:
Given : a12 = a + 11d = 37
d = 3
So, a12 = a + 11 × 3 = 37
a + 33 = 37
a = 37 – 33 = 4
Now, Sn = \(\frac{\mathrm{n}}{2}\)(a + l)
S12 = \(\frac{12}{2}\)[4 + 37] = 6 × 41 = 246.
![]()
iv) Given a3 = 15, S10 = 125, find d and a10.
Solution:
Given : a3 = a + 2d = 15
⇒ a = 15 – 2d —- (1)
S10 = 125 but take S10 as 175
i.e., S10 = 175
We know that,
Sn = \(\frac{\mathrm{n}}{2}\)(a + l)
⇒ S10 = \(\frac{10}{2}\)[a + l]
⇒ 175 = \(\frac{10}{2}\)[2a + 9d]
⇒ 175 = 5[2a + 9d]
⇒ 35 = 2(15 – 2d) + 9d [∵ a = 15 – 2d]
⇒ 35 = 30 – 4d + 9d
⇒ 35 – 30 = 5d ⇒ d = \(\frac{5}{5}\) = 1
Substituting d = 1 in equation (1) we get
a = 15 – 2 × 1 = 15 – 2 = 13
Now, an = a + (n – 1) d
a10 = a + 9d = 13 + 9 × 1
= 13 + 9 = 22
∴ a10 = 22 ; d = 1.
v) Given a = 2, d = 8, Sn = 0, find n and an.
Solution:
Given : a = 2; d = 8 and Sn = 90
But Sn = \(\frac{\mathrm{n}}{2}\)[2a + (n – 1) d]
⇒ 90 = \(\frac{\mathrm{n}}{2}\)[2 × 2 + (n – 1) × 8]
⇒ 90 = \(\frac{\mathrm{n}}{2}\)[4 + 8n – 8]
⇒ 90 = \(\frac{\mathrm{n}}{2}\)[8n – 4]
⇒ 90 = \(\frac{4 n}{2}\)[2n – 1]
⇒ 90 = 2n[2n – 1]
⇒ 4n2 – 2n – 90 = 0
⇒ 2(2n2 – n – 45) = 0
⇒ 2n2 – n – 45 = 0
⇒ 2n2 – 10n + 9n – 45 = 0
⇒ 2n(n – 5) + 9(n – 5) = 0
⇒ (n – 5) (2n + 9) = 0
⇒ n – 5 = 0 (or) 2n + 9 = 0
⇒ n = 5 (or) n = \(\frac{-9}{2}\) (discarded)
∴ n = 5
Now an = a5 = a + 4d = 2 + 4 × 8
= 2 + 32 = 34.
vi) Given an = 4, d = 2, Sn = -14, find n and a.
Solution:
Given an = a + (n – 1) d = 4 —– (1)
d = 2; Sn = -14
From (1); a + (n – 1) 2 = 4
a = 4 – 2n + 2 ⇒ a = 6 – 2n
Sn = \(\frac{\mathrm{n}}{2}\) [a + an]
-14 = \(\frac{\mathrm{n}}{2}\) [(6 – 2n) + 4] [∵ a = 6 – 2n]
-14 × 2 = n(10 – 2n)
⇒ 10n – 2n2 = -28
⇒ 2n2 – 10n – 28 = 0
⇒ n2 – 5n – 14 = 0
⇒ n2 – 7n + 2n – 14 = 0
⇒ n(n – 7) + 2(n – 7) = 0
⇒ (n – 7) (n + 2) = 0
⇒ n = 7 (or) n = – 2
∴ n = 7
Now a = 6 – 2n = 6 – 2 × 7
= 6 – 14 = -8
∴ a = – 8; n = 7.
vii) Given l = 28, S = 144 and there are total 9 terms. Find a.
Solution:
Given :
l = a9 = a + 8d = 28 and S9 = 144
But, Sn = \(\frac{9}{2}\)(a + l)
144 = \(\frac{9}{2}\)[a + 28]
⇒ 144 × \(\frac{2}{9}\) = a + 28
⇒ a + 28 = 32
⇒ a = 32 – 28 = 4.
Question 4.
The first and the last terms of an A.P are 17 and 350 respectively. If the common difference is 9, how many terms are there and what is their sum ?
Solution:
Given A.P in which a = 17
Last term = l = 350
Common difference, d = 9
We know that, an = a + (n – 1) d
350 = 17 + (n – 1)9
⇒ 350 = 17 + 9n – 9
⇒ 9n = 350 – 8
⇒ n = \(\frac{342}{9}\) = 38
Now, Sn = \(\frac{n}{2}\)(a + l)
S38 = \(\frac{38}{2}\)[17 + 350]
= 19 × 367 = 6973
∴ n = 38
Sn = 6973.
Question 5.
Find the sum of first 51 terms of an AP whose second and third terms are 14 and 18 respectively.
Solution:
Given A.P in which
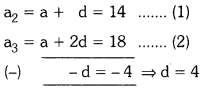
Substituting d = 4 in equation (1), we get a + 4 = 14
⇒ a = 14 – 4 = 10
Now, Sn = \(\frac{n}{2}\)[a + l] (or) \(\frac{n}{2}\) [2a (n – 1) d]
∴ S51 = \(\frac{51}{2}\)[2 × 10 + (51 – 1) × 4]
= \(\frac{51}{2}\)[20 + 50 × 4]
= \(\frac{51}{2}\) × (20 + 200)
= \(\frac{51}{2}\) × 220
= 51 × 110 = 5610.
Question 6.
If the sum of first 7 terms of an AP is 49 and that of 17 terms is 289, find the sum of first n terms. (T.S. & A.P. Mar. 15, 16)
Solution:
Given :
A.P such that S7 = 49
S17 = 289
We know that,
Sn = \(\frac{n}{2}\)[2a + (n – 1)d]
S7 = 49 = \(\frac{7}{2}\)[2a + (7 – 1) d]
⇒ \(\frac{49}{7}\) = \(\frac{1}{2}\)[2a + 6d]
⇒ 7 = a + 3d —– (1)
Also, S17 = 289 = \(\frac{17}{2}\) [2a + (17 – 1)d]
\(\frac{289}{17}\) = \(\frac{1}{2}\)(2a + 16d)
⇒ 17 = a + 8d —— (2)
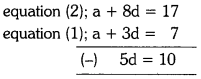
⇒ d = \(\frac{10}{5}\)
Substituting d = 2 in equation (1), we get
a + 3 × 2 = 7
⇒ a = 7 – 6 = 1
∴ a = 1; d = 2
Now, Sn = \(\frac{\mathrm{n}}{2}\)[2a + (n – 1)d]
Sn = \(\frac{\mathrm{n}}{2}\) [2 × 1 + (n -1)2]
= \(\frac{\mathrm{n}}{2}\) [2 + 2n – 2)d] = \(\frac{\mathrm{n} .2 \mathrm{n}}{2}\)
∴ Sum of first n terms Sn = n2.
Shortcut : S7 = 49 = 72
S17 = 289 = 172
∴ Sn = n2
Question 7.
Show that a1, a2, ……. an, …. form an AP where an is defined as below :
i) an = 3 + 4n
ii) an = 9 – 5n. Also find the sum of the first 15 terms in each case.
Solution:
i) Given an = 3 + 4n
Then a1 = 3 + 4 × 1 = 3 + 4 = 7
a2 = 3 + 4 × 2 = 3 + 8 = 11
a3 = 3 + 4 × 3 = 3 + 12 = 15
a4 = 3 + 4 × 4 = 3 + 16 = 19
Now the pattern is 7, 11, 15, ……..
where a = a1 = 7; a2 = 11; a3 = 15, …. and a2 – a1 = 11 – 7 = 4;
a3 – a2 = 15 -11 = 4; Here d = 4. Hence a1, a2, …., an … forms an A.P.
s15 = \(\frac{15}{2}\) [2 × 7 + (15 – 1)4]
= \(\frac{15}{2}\) [14 + 14.4] = \(\frac{15}{2}\) [70]
= 15 × 35 = 525.
![]()
ii) an = 9 – 5n
Solution:
Given : an = 9 – 5n
a1 = 9 – 5 × 1 = 9 – 5 = 4
a2 = 9 – 5 × 2 = 9 – 10 = -1
a3 = 9 – 5 × 3 = 9 – 15 = -6
a4 = 9 – 5 × 4 = 9 – 20 = -11
………………………………..
Also a2 – a1 = -1 – 4 = – 5
a3 – a2 = – 6 – (-1) = – 6 + 1 = -5
a4 – a3 = – 11 – (- 6)
= -11 + 6
= -5
∴ d = a2 – a1 = a3 – a2
= a4 – a3 = ……. = -5
Thus the difference between any two succes-sive terms is constant.
Hence {an} forms A.P.
S15 = \(\frac{15}{2}\)[2 × 4 + (15 – 1) × (-5)]
= \(\frac{15}{2}\) [8 + 14 (-5)] = \(\frac{15}{2}\) × -62
= 15 × – 31 = – 465.
Question 8.
If the sum of the first n terms of an AP is 4n – n2, what is the first term (remember the first term is S1) ? What is the sum of first two terms ? What is the second term ? Similarly, find the 3rd, the 10th and the nth terms.
Solution:
Given an A.P in which S<sub?n = 4n – n2
Taking n = 1 we get
S1 = 4 × 1 – 12 = 4 – 1 = 3
n = 2; S2 = a1 + a2 = 4 × 2 – 22
= 8 – 4 = 4
n = 3; S3 = a1 + a2 + a3
= 4 × 3 – 32 = 12 – 9 = 3
n = 4; S4 = a1 + a2 + a3 + a4
= 4 × 4 – 42 = 16 – 16 = 0
Hence, S1 = a1 = 3
∴ a2 = S2 – S1 = 4 – 3 = 1
a3 = S3 – S2 = 3 – 4 = -1
a4 = S4 – S3 = 0 – 3 = -3
So, d = a2 – a1 = 1 – 3 = -2
Now, a10 = a + 9d [∴ an = a + (n – 1) d]
= 3 + 9 × (- 2)
= 3 – 18 = -15
an = 3 + (n – 1) × (-2)
= 3 – 2n + 2 = 5 – 2n.
Question 9.
Find the sum of the first 40 positive integers divisible by 6.
Solution:
The given numbers are the first 40 positive multiples of 6
⇒ 6 × 1, 6 × 2, 6 × 3, ……., 6 × 40
⇒ 6, 12, 18, …… 240
Sn = \(\frac{\mathrm{n}}{2}\) [a + l]
= \(\frac{40}{2}\) [6 + 240]
= 20 × 246 = 4920
∴ S40 = 4920.
Question 10.
A sum of ₹ 700 is to be used to give seven cash prizes to students of a school for their overall academic performance. If each prize is ₹ 20 less than its preceding prize, find the value of each of the prizes.
Solution:
Given :
Total l Sum of all cash prizes = ₹ 700
Each prize differs by ₹ 20
Let the prizes (in ascending order) be
x, x + 20, x + 40, x + 60, x + 80, x + 100, x + 120
∴ Sum of the prizes = S7 = \(\frac{\mathrm{n}}{2}\) [a + l]
⇒ 700 = \(\frac{7}{2}\) [x + x + 120]
⇒ 700 × \(\frac{2}{7}\) = 2x + 120
⇒ 100 = x + 60
⇒ x = 100 – 60 = 40
∴ The prizes are 160, 140, 120, 100, 80, 60, 40.
Question 11.
In a school, students thought of planting trees in and around the school to reduce air pollution. It was decided that the number of trees, that each section of each class will plant, will be the same as the class, in which they are studying, e.g : a section of Class I will plant 1 tree, a section of Class 11 will plant 2 trees and so on till Class XII. There are three sections of each class. How many trees will be planted by the students ?
Solution:
Given : Classes : From I to XII
Section : 3 in each class.
∴ Trees planted by each class = 3 × class number

∴ Total trees planted = 3 + 6 + 9 + 12 + ………+ 36; n = 12
∴ Sn = \(\frac{\mathrm{n}}{2}\) [a + l]
S12 = \(\frac{12}{2}\) [3 + 36]
= 6 × 39 = 234
∴ Total plants = 234
![]()
Question 12.
A spiral is made up of successive semicircles, with centres alternately at A and B, starting with centre at A, of radii 0.5 cm, 1.0 cm, 1.5 cm, 2.0 cm, … as shown in figure. What is the total length of such a spiral made up of thirteen consecutive semicircles ? (Take π = \(\frac{22}{7}\))
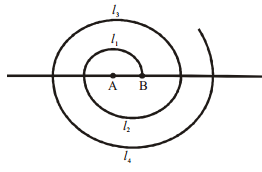
[Hint: Length of successive semi-circles is l1, l2, l3, l4,……… with centres at A, B, A, B,…., respectively.]
Solution:
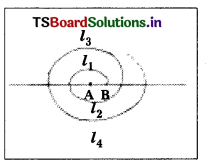
Given : l1; l2, l3, l4, …….l13 are the semi-circles
with centres alternately at A and B; with radii
r1 = 0.5 cm [1 × 0.5]
r2 = 1.0 cm [2 × 0.5]
r3 = 1.5 cm [3 × 0.5]
r4 = 2.0 cm [4 × 0.5]
………………………..
r13 = 13 × 0.5 = 6.5
[∴ Radii are in A.P. as a1 = 0.5 and d = 0.5]
Now, the total length of the spiral = l1 + l2 +….. + l13 [… 13 given]
But circumference of a semi-circle is πr.
∴ Total length of the spiral = π × 0.5 + π × 1.0 + ……… + π × 6.5
= π × \(\frac{1}{2}\)[1 + 2 + 3 + ……. + 13]
Sum of the first n – natural numbers is \(\frac{\mathrm{n}(\mathrm{n}+1)}{2}\)]
Question 13.
200 logs are stacked in the following manner : 20 logs in the bottom row, 19 in the next row, 18 in the row next to it and so on. In how many rows are the 200 logs placed and how many logs are in the top row ?

Solution:
Given : Total logs = 200
Number of logs stacked in the first row = 20
Number of logs stacked in the second row = 19
Number of logs stacked in the third row = 18
………………………………
The number series is 20, 19, 18, …. is an A.P.
where a = 20 and d = a2 – a1 = 19 – 20 = -1
Also, Sn = 200
∴ Sn = \(\frac{n}{2}\) [2a + (n – 1)d]
200 = \(\frac{n}{2}\) [2 × 20 + (n – 1) × (-1)]
200 = \(\frac{n}{2}\) [40 – n + 1]
200 = \(\frac{n}{2}\) [41 – n]
400 = 41n – n2
⇒ n2 – 41n + 400 = 0
⇒ n2 – 25n – 16n + 400 = 0
⇒ n(n – 25) – 16(n – 25) = 0
⇒ (n – 25) (n – 16) = 0
⇒ n = 25 (or) 16
There can’t be 25 rows as we are starting with 20 logs in the first row.
∴ Number of rows must be 16.
∴ n = 16 and t16 = a + (n – 1) d = 20 + (16 – 1) (-1) = 20 – 15 = 5
Question 14.
In a bucket and ball race, a bucket is placed at the starting point, which is 5 m from the first ball, and the other balls are placed 3 m apart in a straight line. There are ten balls in the line.

A competitor starts from the bucket, picks up the nearest ball, runs back with it, drops it in the bucket, runs back to pick up the next ball, runs to the bucket to drop it in, and she continues in the same way until all the balls are in the bucket. What is the total distance the competitor has to run ?
[Hint : To pick up the first ball and the second ball, the total distance (in metres) run by a competitor is 2 × 5 + 2 × (5 + 3)]
Solution:
Given : Balls are placed at an equal distance of 3 m from one another.
Distance of first ball from the bucket = 5 m
Distance of second ball from the bucket = 5 + 3 = 8m (5 + 1 × 3)
Distance of third ball from the bucket = 8 + 3 = 11 m (5 + 2 × 3)
Distance of fourth ball from the bucket = 11 + 3 = 14m (5 + 3 × 3)
…………………………………………………..
∴ Distance of the tenth ball from the bucket = 5 + 9 × 3 = 5 + 27 = 32m.
1st ball: Distance covered by the competitor in picking up and dropping it in the bucket = 2 × 5 = 10 m.
2nd ball : Distance covered by the competitor in picking up and dropping it in the bucket = 2 × 8 = 16 m.
3rd ball : Distance covered by the competitor in picking up and dropping it in the bucket = 2 × 11 = 22 m.
……………………………………………………
10th ball: Distance covered by the competitor in picking up and dropping it in the bucket = 2 × 32 = 64 m
Total distance = 10 m + 16 m + 22 m +………….+ 64 m.
Clearly, this is an A.P in which a = 10; d = a2 – a1 = 16 – 10 = 6 and n = 10.
Sn = \(\frac{\mathrm{n}}{2}\) [2a + (n – 1)d]
= \(\frac{10}{2}\) [2 × 10 + (10 – 1) × 6]
= 5[20 + 54] = 5 × 74 = 370 m
∴ Total distance = 370 m.