Students must practice these Maths 1B Important Questions TS Inter First Year Maths 1B Straight Lines Important Questions Long Answer Type to help strengthen their preparations for exams.
TS Inter First Year Maths 1B Straight Lines Important Questions Long Answer Type
Question 1.
If Q(h, k) is foot of the perpendicular from P(x1, y1) on the straight line ax + by + c = 0 then show that \(\frac{h-x_1}{a}=\frac{k-y_1}{b}=\frac{-\left(a x_1+b y_1+c\right)}{a^2+b^2}\). [May ’14, ’07; Mar. ’03]
Solution:
Let A(x1, y1), P(h, k)
‘P’ lies in ax + by + c = 0 then
ah + bk + c = 0
ah + bk = -c



Question 2.
Find the foot of the perpendicular from (-1, 3) on the straight line 5x – y – 18 = 0. [May ’13 (old), ’07: Mar. ’03]
Solution:
Given the equation of the straight line is 5x – y – 18 – 0
Comparing with ax + by + c = 0, we get
a = 5, b = -1, c = -18
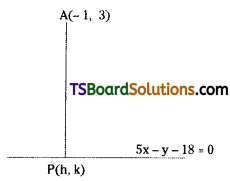
Let the given point A(x1, y1) = (-1, 3)
Let (h, k) is the foot perpendicular from the point A(-1, 3) on line 5x – y – 18 = 0

∴ Foot of the perpendicular P(h, k) = (4, 2)
![]()
Question 3.
If Q(h, k) is the image of the point p(x1, y1) with respect to the straight line ax + by + c = 0 then, show that \(\frac{h-\mathbf{x}_1}{\mathbf{a}}=\frac{\mathbf{k}-\mathbf{y}_1}{\mathbf{b}}=\frac{-2\left(a \mathbf{x}_1+\mathbf{b y}_1+\mathbf{c}\right)}{a^2+b^2}\). [Mar. ’19 (AP); Mar. ’13, ’04, ’93; May ’06, ’01]
Solution:
Let A(x1, y1), B(h, k)
‘C’ is the midpoint of \(\overline{\mathrm{AB}}\) then
C = \(\left(\frac{\mathrm{x}_1+\mathrm{h}}{2}, \frac{\mathrm{y}_1+\mathrm{k}}{2}\right)\)
‘B’ is the image of A, then midpoint ‘C’ lies on ax + by + c = 0


Question 4.
Find the image of (1, -2) with respect to the straight line 2x – 3y + 5 = 0. [Mar. ’13]
Solution:
Given the equation of the straight line is 2x – 3y + 5 = 0
Comparing with ax + by + c = 0, we get
a = 2, b = -3, c = 5
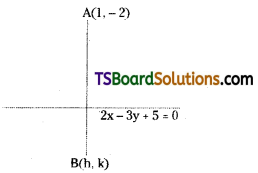
Let the given point A(x1, y1) = (1, -2)
Now, B(h, k) be the image of A(1, -2) with respect to the straight line 2x – 3y + 5 = 0
\(\frac{h-x_1}{a}=\frac{k-y_1}{b}=\frac{-2\left(a x_1+b y_1+c\right)}{a^2+b^2}\)

∴ Image of B(h, k) = (-3, 4)
Question 5.
Find the equation of the straight lines passing through the point (-3, 2) and making an angle of 45° with the straight line 3x – y + 4 = 0. [Mar. ’09]
Solution:
Given, equation of the straight line is 3x – y + 4 = 0 ……..(1)
slope of the line (1) is m = \(\frac{-3}{-1}\) = 3
Let the given point A = (-3, 2)
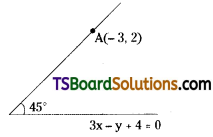
Let the slope of the required line is m2 = m
∴ The equation of the required line is passed through (-3, 2), and having slope m is y – y1 = m(x – x1)
y – 2 = m(x + 3) …….(2)
y – 2 = mx + 3m
mx – y + (3m + 2) = 0
Given that the angle between the lines is 45°,
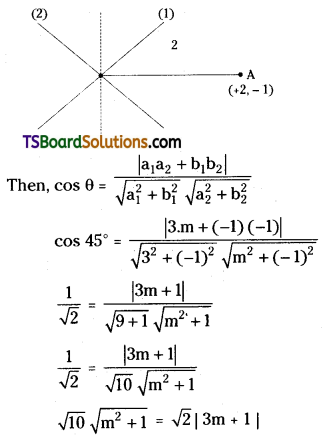
Squaring on both sides
⇒ 10(m2 + 1) = 2(9m2 + 6m + 1)
⇒ 10m2 + 10 = 18m2 + 12m + 2
⇒ 8m2 + 12m – 8 = 0
⇒ 2m2 + 3m – 2 = 0
⇒ 2m2 + 4m – m – 2 = 0
⇒ (m + 2) (2m – 1) = 0
⇒ m + 2 = 0 (or) 2m – 1 = 0
⇒ m = -2 (or) \(\frac{1}{2}\)
If m = -2,
(2) ⇒ y – 2 = m(x + 3)
y – 2 = -2x – 6
2x + y + 4 = 0
If m = \(\frac{1}{2}\),
(2) ⇒ y – 2 = \(\frac{1}{2}\)(x + 3)
2y – 4 = x + 3
x – 2y + 7 = 0
∴ The equation of the straight line is 2x + y + 4 = 0
∴ The equation of straight line is x – 2y + 7 = 0
∴ The required equations of the straight line are, 2x + y + 4 = 0, x – 2y + 7 = 0
![]()
Question 6.
Find the equations of the straight lines passing through the point of intersection of the lines 3x + 2y + 4 = 0, 2x + 5y = 1 and whose distance from (2, -1) is 2. [May ’09; Mar. ’09]
Solution:
Given equations of the straight lines are
3x + 2y + 4 = 0 ……….(1)
2x + 5y – 1 = 0 ………(2)
Let the given point A = (2, -1)
∴ The equation of the straight line passing through the point of intersection of lines is (1) & (2) is L1 + λL2 = 0
(3x + 2y + 4) + λ(2x + 5y – 1) = 0 ……(3)
3x + 2y + 4 + 2λx + 5λy – λ = 0
(3 + 2λ)x + (2 + 5λ)y + (4 – λ) = 0
Given that the perpendicular distance from point A(2, -1) to the line (3) is 2.

squaring on both sides
(-λ + 4)2 = 29λ2 + 32λ + 13
λ2 + 16 – 8λ = 29λ2 + 32λ + 13
28λ2 + 40λ – 3 = 0
28λ2 + 42λ – 2λ – 3 = 0
14λ(2λ + 3) – 1(2λ + 3) = 0
(2λ + 3) (14λ – 1) = 0
(2λ + 3) = 0, 14λ – 1 = 0
λ = \(\frac{-3}{2}\); λ = \(\frac{1}{14}\)
Case I: If λ = \(\frac{-3}{2}\), then
The equation of the straight line is from (3)
(3x + 2y + 4) + (\(\frac{-3}{2}\)) (2x + 5y – 1) = 0
\(\frac{6 x+4 y+8-6 x-15 y+3}{2}=0\)
-11y + 11 = 0
y – 1 = 0
If λ = \(\frac{1}{14}\), then
The equation of the straight line is from (3)
(3x + 2y + 4) + (\(\frac{1}{14}\)) (2x + 5y – 1) = 0
\(\frac{42 x+28 y+56+2 x+5 y-1}{14}=0\)
44x + 33y + 55 = 0
4x + 3y + 5 = 0
∴ The required equations of the straight lines are y – 1 = 0 & 4x + 3y + 5 = 0
Question 7.
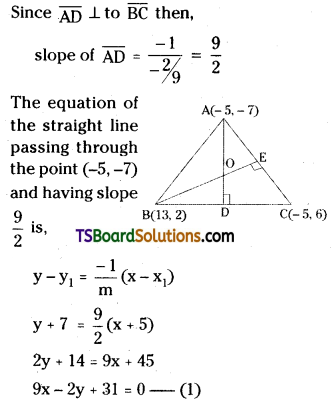
Find the orthocentre of the triangle whose vertices are (-5, -7), (13, 2), and (-5, 6). [Mar. ’16 (AP) ’12, ’03; May ’98]
Solution:
Let A(-5, -7), B(13, 2), C(-5, 6) are the given points.
The equation of the altitude \(\overline{\mathbf{A D}}\).
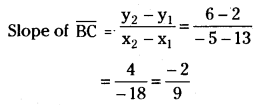

Question 8.
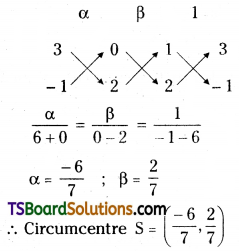
Find the circumcentre of the triangle whose vertices are (-2, 3), (2, -1) and (4, 0). [Mar. ’17 (AP), ’13 (Old), ’11; May ’15 (TS), ’02, ’92]
Solution:
Let A(-2, 3), B(2, -1), C(4, 0) are the given points
Let S(α, β) be the circumcentre of the triangle ABC
then, SA = SB = SC
Now, SA = SB
⇒ SA2 = SB2
⇒ (α + 2)2 + (β – 3)2 = (α – 2)2 + (β + 1)2
⇒ α2 + 4 + 4α + β2 + 9 – 6β = α2 + 4 – 4α + β2 + 1 + 2β
⇒ 4α + 9 – 6β + 4α – 1 – 2β = 0
⇒ 8α – 8β + 8 = 0
⇒ α – β + 1 = 0 …….(1)
Also SB = SC
⇒ SB2 = SC2
⇒ (α – 2)2 + (β + 1)2 = (α – 4)2 + (β – 0)2
⇒ α2 + 4 – 4α + β2 + 2β + 1 = α2 + 16 – 8α + β2
⇒ 4 – 4α + 2β + 1 – 16 + 8α = 0
⇒ 4α + 2β – 11 = 0 ……(2)
Solving (1) & (2)

Question 9.
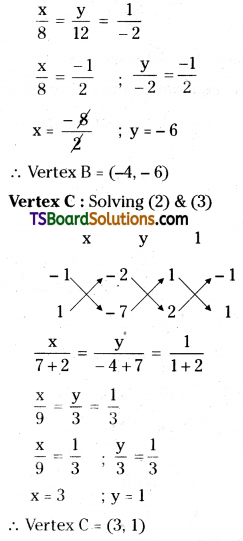
Find the orthocentre of the triangle whose sides are given by x + y + 10 = 0, x – y – 2 = 0, and 2x + y – 7 = 0. [May ’13]
Solution:



![]()
Question 10.
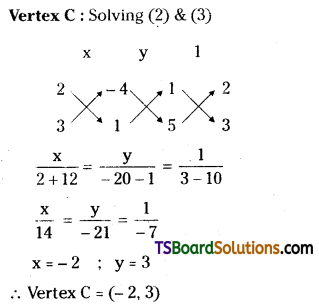
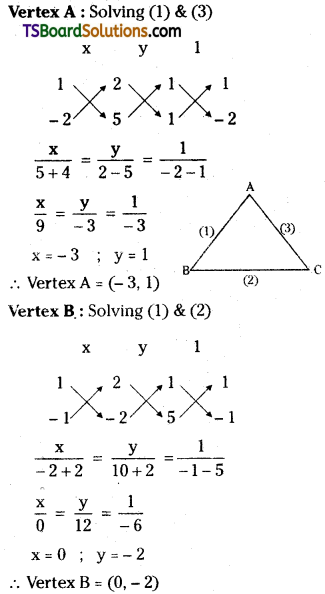
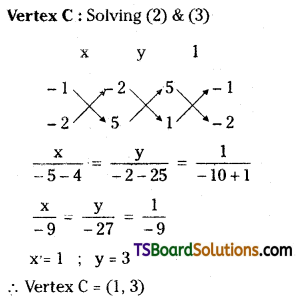
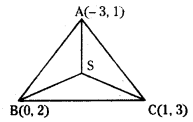
Find the circumcentre of the triangle whose sides are 3x – y – 5 = 0, x + 2y – 4 = 0 and 5x + 3y + 1 = 0. [May ’11, ’05; Mar. ’06]
Solution:
Given, the equations of the straight lines are
3x – y – 5 = 0 ……..(1)
x + 2y – 4 = 0 ……..(2)
5x + 3y + 1 = 0 ……..(3)
Vertex A: Solving (1) & (3)

Let S(α, β) be the circumcentre then SA = SB = SC
Now, SA = SB
⇒ SA2 = SB2
⇒ (α – 1)2 + (β + 2)2 = (α – 2)2 + (β – 1)2
⇒ α2 – 2α + 1 + β2 + 4 + 4β = α2 + 4 – 4α + β2 + 1 – 2β
⇒ -2α + 4β + 4α + 2β = 0
⇒ 2α + 6β = 0
⇒ α + 3β = 0 ……..(4)
Also SB = SC
⇒ SB2 = SC2
⇒ (α – 2)2 + (β – 1)2 = (α + 2)2 + (β – 3)2
⇒ α2 – 2α + 1 + β2 – 2β + 1 = α2 + 4α + 4 + β2 – 6β + 9
⇒ 4α + 9 – 6β + 4α – 1 + 2β = 0
⇒ 8α – 4β – 8 = 0
⇒ 2α – β + 2 = 0 ……..(5)
Solving (1) & (2)
Question 11.
Find the equations of the straight lines passing through the point (1, 2) and make an angle of 60° with the line √3x + y + 2 = 0. [May ’03; B.P.]
Solution:
Given, equation of the straight line is √3x + y + 2 = 0 ……….(1)
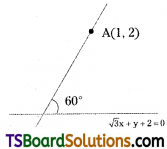
Let the given point A(x1, y1) = (1, 2)
Given that θ = 60°
Let the slope of the required straight line is = m
∴ The equation of the straight line is passed through A(1, 2) and having slope ‘m’ is y – y1 = m(x – x1)
y – 2 = m(x – 1) …….(2)
y – 2 = mx – m
mx – y – m + 2 = 0
Let ‘θ’ be the angle between the lines (1) & (2)

Squaring on both sides
⇒ m2 + 1 = (√3m – 1)2
⇒ m2 + 1 = 3m2 + 1 – 2√3m
⇒ 2m2 – 2√3m = 0
⇒ m2 – √3m = 0
⇒ m(m – √3) = 0
⇒ m = 0 (or) m – √3 = 0
⇒ m = 0 (or) m = √3
Case 1: If m = 0 then, the equation of a required straight line is,
from (2), y – 2 = 0(x – 1)
y – 2 = 0
y = 2
Case 2: If m = √3 then, the equation of a required straight line is
from (2), y – 2 = √3(x – 1)
y – 2 = √3x – √3
√3x – y + 2 – √3 = 0
∴ The equations of the required straight lines are y = 2 and √3x – y + 2 – √3 = 0
Question 12.
If p and q are the lengths of the perpendiculars from the origin to the straight lines x sec α + y cosec α = a and x cos α – y sin α = a cos 2α prove that 4p2 + q2 = a2. [Mar. ’13 (Old), ’08; May ’13]
Solution:
Given, the equations of the straight lines are
x sec α + y cosec α – a = 0 …….(1)
x cos α – y sin α = a cos 2α ……….(2)
Let the point p(x1, y1) = (0, 0)
Now, p = the perpendicular distance from the point p(0, 0) to the straight line (1)
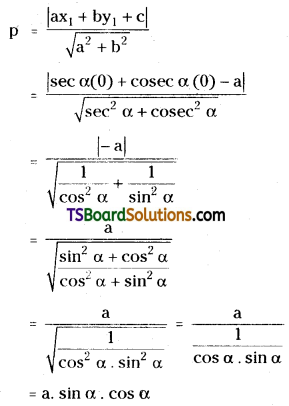
q = the perpendicular distance from the point p(0, 0) to the straight line (2)
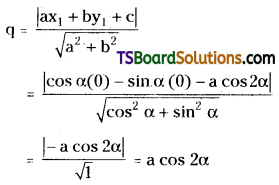
L.H.S = 4p2 + q2
= 4(a sin α cos α)2 + (a cos 2α)2
= 4a2 sin2α cos2α + a2 cos2 2α
= a2(2 sin α cos α)2 + a2 cos2 2α
= a2 sin2 2α + a2 cos2 2α
= a2(sin2 2α + cos2 2α)
= a2
= R.H.S
∴ 4p2 + q2 = a2
Some More Maths 1B Straight Lines Important Questions
Question 13.
Find the equation of the straight line which makes an angle 135° with the positive X-axis measured counterclockwise and passing through the point (-2, 3).
Solution:
Given that, the inclination of a line is θ = 135°
The slope of a straight line is, m = tan θ
= tan 135°
= tan (180° – 45°)
= -tan 45°
= -1
Let the given point A(x1, y1) = (-2, 3)
∴ The equation of the straight line passing through the point (-2, 3) and having slope ‘-1’ is,
y – y1 = m(x – x1)
y – 3 = -1(x + 2)
y – 3 = -x – 2
x + y – 1 = 0
Question 14.
Find the equation of the straight line passing through the point (2, 3) and making non-zero intercepts on the axes of coordinates whose sum is zero. [Mar. ’12; May ’09]
Solution:
The equation of a straight line in the intercept form is
\(\frac{x}{a}+\frac{y}{b}\) = 1 ………(1)
Given that, the sum of the intercepts = 0
a + b = 0
b = -a
From (1), \(\frac{x}{a}+\frac{y}{-a}=1\)
x – y = a ……(2)
Since equation (2) passes through the point (2, 3) then,
2 – 3= a
∴ a = -1
Substitute the value of ‘a’ in equation (2)
x – y = -1
x – y + 1 = 0
∴ The equation is x – y + 1 = 0.
![]()
Question 15.
Find the equation of the straight line passing through points (4, -3) and perpendicular to the line passing through points (1, 1) and (2, 3).
Solution:
Let A(1, 1), B(2, 3), C(4, -3) are the given points
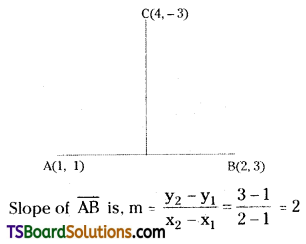
Slope of the perpendicular line = \(\frac{-1}{m}=\frac{-1}{2}\)
∴ The equation of the straight line passing through C(4, -3) and having slope \(\frac{-1}{2}\) is y – y1 = \(\frac{1}{m}\) (x – x1)
y + 3 = \(\frac{-1}{2}\) (x – 4)
2y + 6 = -x + 4
x + 2y+ 6 – 4 = 0
x + 2y + 2 = 0
Question 16.
Transform the equation 3x + 4y + 12 = 0 into (i) slope-intercept form (ii) intercept form (iii) normal form.
Solution:
(i) Slope-intercept form:
Given, the equation of the straight line is 3x + 4y + 12= 0
4y = -3x – 12
y = \(\frac{-3 x}{4}-\frac{12}{4}=\left(\frac{-3}{4}\right) x+(-3)\)
which is in the form of y = mx + c
Slope, m = \(\frac{-3}{4}\), y-intercept, c = -3
(ii) Intercept form:
Given, the equation of the straight line is 3x + 4y + 12 =0
3x + 4y = -12 × 1
\(\frac{3 x}{-12}+\frac{4 y}{-12}=1\)
\(\frac{x}{-4}+\frac{y}{-3}=1\)
which is in the form of \(\frac{x}{a}+\frac{y}{b}=1\)
∴ x-intercept, a = -4, y-intercept, b = -3
(iii) Normal form:
Given the equation of the straight line is, 3x + 4y + 12 = 0
3x + 4y= -12
-3x – 4y = 12
On dividing both sides with \(\sqrt{a^2+b^2}\)

which is in the form x cos α + y sin α = p
∴ cos α = \(\frac{-3}{5}\), sin α = \(\frac{-4}{5}\), p = \(\frac{12}{5}\)
Question 17.
Find the distance between the parallel straight lines 5x – 3y – 4 = 0, 10x – 6y – 9 = 0. [Mar. ’13(old), ’09, ’02; May ’12]
Solution:
Given, the equations of the straight lines are
5x – 3y – 4 = 0
10x – 6y – 9 = 0 …….(2)
2(5x – 3y – 4) = 0
10x – 6y – 8 = 0 ………(1)
Comparing (1) with ax + by + c1 = 0, we get
a = 10, b = -6, c1 = -8
Comparing (2) with ax + by + c2 = 0, we get
a = 10, b = -6, c2 = -9
Distance between the parallel lines =
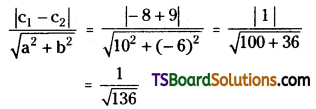
Question 18.
Find the value of p, if the straight lines 3x + 7y – 1 = 0 and 7x – py + 3 = 0 are mutually perpendicular.
Solution:
Given, the equations of the straight lines are
3x + 7y – 1 = 0 ……..(1)
7x – py + 3 = 0 ……..(2)
Slope of the line (1) is m1 = \(\frac{-3}{7}\)
Slope of the line (2) is m2 = \(\frac{-7}{-p}=\frac{7}{p}\)
Since the given lines are perpendicular then,
m1 × m2 = -1
\(\frac{-3}{7} \times \frac{7}{p}\) = -1
p = 3
![]()
Question 19.
Find the value of p, if the lines 3x + 4y = 5, 2x + 3y = 4, px + 4y = 6 are concurrent. [May ’06]
Solution:
Given, the equations of the straight lines are,
3x + 4y – 5 = 0 ……..(1)
2x + 3y – 4 = 0 ……..(2)
px + 4y – 6 = 0 …….(3)
Solving (1) & (2)
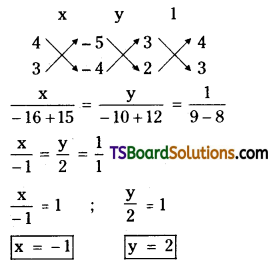
∴ The point of intersection of the straight lines (1) & (2) is (-1, 2)
Now, given lines are concurrent then, the point of intersection lies on the line
p(-1) + 4(2) – 6 = 0
-p + 8 – 6 = 0
-p + 2 = 0
p = 2
Question 20.
Find the value of p, if the lines 4x – 3y – 7 = 0, 2x + py + 2 = 0, 6x + 5y – 1 = 0 are concurrent.
Solution:
Given, the equations of the straight lines are,
4x – 3y – 7 = 0 …….(1)
2x + py + 2 = 0 ……..(2)
6x + 5y – 1 = 0 ……….(3)
Solving (1) & (3)
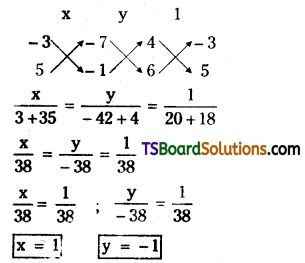
∴ The point of intersection of the straight lines (1) & (3) is, (1, -1).
Since the given lines are concurrent, then the point of intersection (1, -1) lies on line (2).
2(1) + p(-1) + 2 = 0
2 – p + 2 = 0
4 – p = 0
p = 4
Question 21.
Show that the lines 2x + y – 3 = 0, 3x + 2y – 2 = 0 and 2x – 3y – 23 = 0 are concurrent and find the point of concurrent.
Solution:
Given, the equations of the straight lines are,
2x + y – 3 = 0 …….(1)
3x + 2y – 2 = 0 ……….(2)
2x – 3y – 23 = 0 ………(3)
Solving (1) & (2)
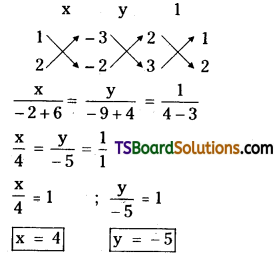
∴ The point of intersection of the straight lines (1) & (2) is (4, -5).
Now substitute the point (4, -5) in equation (3)
2(4) – 3(-5) – 23 = 0
8 + 15 – 23 = 0
23 – 23 = 0
0 = 0
∴ Given lines are concurrent.
∴ Point of concurrence = (4, -5).
Question 22.
A straight line meets the coordinate axes in A and B. Find the equation of the straight line, when \(\overline{\mathbf{A B}}\) is divided in the ratio 2 : 3 at (-5, 2).
Solution:
The equation of the straight line in the intercept form is \(\frac{x}{a}+\frac{y}{b}=1\) ……..(1)
The straight line (1) meets the X-axis at A(a, 0), Y-axis at B(0, b).
Now, P(-5, 2) divides \(\overline{\mathbf{A B}}\) in the ratio 2 : 3
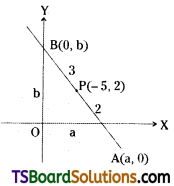

Question 23.
A straight line meets the coordinate axes in A and B. Find the equation of the straight line when \(\overline{\mathbf{A B}}\) is divided in the ratio 1 : 2 at (-5, 4).
Solution:
The equation of the straight line in the intercept form is \(\frac{x}{a}+\frac{y}{b}=1\) ……..(1)
The straight line (1) meets the X-axis at A(a, 0), Y-axis at B(0, b).
Now, P(-5, 4) divides \(\overline{\mathbf{A B}}\) in the ratio 1 : 2
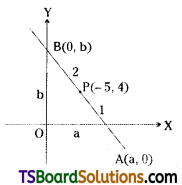

Question 24.
If non-zero numbers a, b, c are in harmonic progression, then show that the equation \(\frac{x}{a}+\frac{y}{b}+\frac{1}{c}=0\) represents a family of concurrent lines and find the point of concurrency.
Solution:
Given that, a, b, c are in harmonic progression.
then, \(\frac{2}{b}=\frac{1}{a}+\frac{1}{c}\)
\(\frac{2}{b}-\frac{1}{a}=\frac{1}{c}\)
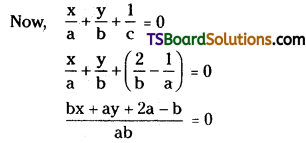
bx + ay + 2a – b = 0
b(x – 1) + a(y + 2) = 0
(x – 1) + \(\frac{a}{b}\) (y + 2) = 0
This is of the form L1 + λL2 = 0
∴ \(\frac{x}{a}+\frac{y}{b}+\frac{1}{c}=0\) represents a set of lines passing through the point of intersection of
L1 = x – 1 = 0 ……..(1)
L2 = y + 2 = 0 ………(2)
Solve (1) & (2)
from (1), x – 1 = 0 ⇒ x = 1
from (2) y + 2 = 0 ⇒ y = -2
∴ The point of concurrence = (1, -2).
∴ \(\frac{x}{a}+\frac{y}{b}+\frac{1}{c}=0\) represents a set of concurrent lines.
![]()
Question 25.
If a, b, c are in arithmetic progression, then show that the equation ax + by + c = 0 represents a family of concurrent lines and find the point of concurrency.
Solution:
Given that, a, b, c are in arithmetic progression, then
2b = a + c
c = 2b – a
Now, ax + by + c = 0
ax + by + (2b – a) = 0
ax + by + 2b – a = 0
a(x – 1) + b(y + 2) = 0
x – 1 + \(\frac{b}{a}\) (y + 2) = 0
This is of the form L1 + λL2 = 0
∴ ax + by + c = 0 represents a set of lines passing through the point of intersection of
L1 = x – 1 = 0 …….(1)
L2 = y + 2 = 0 ……..(2)
Solve (1) & (2)
from (1), x – 1 = 0 ⇒ x = 1
from (2), y + 2 = 0 ⇒ y = -2
∴ The point of concurrence = (1, -2).
∴ ax + by + c = 0 represents a set of concurrent lines.
Question 26.
A straight line parallels the line y = √3x passes through Q(2, 3), and cuts the line 2x + 4y – 27 = 0 at p then, finds the length of PQ.
Solution:
Given the equation of the straight line is y = √3x
This is of the form y = mx
⇒ m = √3
⇒ tan θ = √3
⇒ θ = 60°
Since \(\overline{\mathrm{PQ}}\) is parallel to the straight line y = √3x
∴ Slope of \(\overline{\mathrm{PQ}}\) = √3
Inclination of a straight line \(\overline{\mathrm{PQ}}\), 0 = 60°
Given point Q(x1, y1) = (2, 3)
∴ The coordinates of P = (x1 + r cos θ, y1 + r sin θ)
= (2 + r cos 60°, 3 + r sin 60°)
= (2 + r(\(\frac{1}{2}\)), 3 + \(\frac{\sqrt{3} r}{2}\)) where |r| = PQ
Since the point, ‘p’ lies on the straight line 2x + 4y – 27 = 0

Question 27.
A straight line with slope 1 passes through Q(-3, 5) and meets the line x + y – 6 = 0 at P. Find the distance PQ.
Solution:
Given, equation of the straight line is x + y – 6 = 0 ……….(1)
The slope of the straight line m = 1
Given point Q(x1, y1) = (-3, 5)
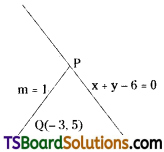
∴ The equation of the straight line \(\overline{\mathrm{PQ}}\) having slope ‘1’ and passes through the point Q(-3, 5) is (y – y1) = m(x – x1)
y – 5 = 1(x + 3)
y – 5 = x + 3
x – y + 8 = 0 …….(2)
Solving (1) & (2)

Question 28.
A straight line through Q(2, 3) makes an angle \(\frac{3 \pi}{4}\) with the negative direction of the X-axis. If the straight line intersects the line x + y – 7 = 0 at P, find the distance PQ.
Solution:
Given, equation of the straight line is x + y – 7 = 0 ……..(1)
Given point Q(x1, y1) = (2, 3)
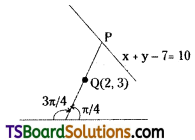
Given that the straight line makes an angle \(\frac{3 \pi}{4}\) with the ‘-ve’ direction of the X-axis, then the straight line makes an angle π – \(\frac{3 \pi}{4}\) = \(\frac{\pi}{4}\) = 45° with the positive direction of X-axis.
∴ The slope of the straight line is m = tan θ
= tan 45°
= 1
The equation of the straight line \(\overline{\mathrm{PQ}}\) having slope ‘1’ and passing through the point Q(2, 3) is,
y – y1 = m(x – x1)
y – 3 = 1(x – 2)
y – 3 = x – 2
x – y + 1 = 0 …….(2)
Solving (1) & (2)
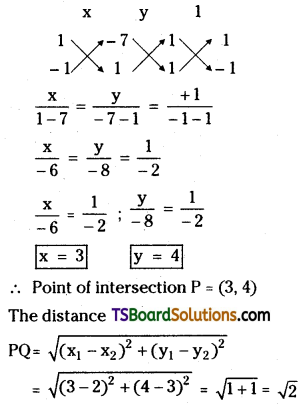
Question 29.
Find the foot of the perpendicular drawn from (4, 1) upon the straight line 3x – 4y + 12 = 0. [May ’08; June ’02]
Solution:
Given the equation of the straight line is 3x – 4y + 12 = 0.
Comparing with ax + by + c = 0, we get
a = 3, b = -4, c = 12
Let the given point A(x1, y1) = (4, 1)
Let (h, k) is the foot perpendicular from the point A(4, 1) on the line 3x – 4y + 12 = 0
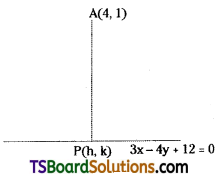

Question 30.
Find the foot of the perpendicular drawn from (3, 0) upon the straight line 5x + 12y – 41 = 0.
Solution:
Given the equation of the straight line is 5x + 12y – 41 = 0
Comparing with ax + by + c = 0, we get
a = 5, b = 12, c = -41
Let the given point A(x1, y1) = (3, 0)
Let (h, k) is the foot of the perpendicular from the point A(3, 0) on the line 5x + 12y – 41 = 0
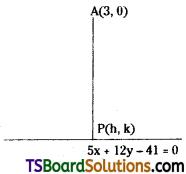

![]()
Question 31.
Find the image of the point (1, 2) in the straight line 3x + 4y – 1 = 0. [Mar. ’07, ’02, ’97; May ’04, ’97]
Solution:
Given the equation of the straight line is 3x + 4y – 1 = 0
Comparing with ax + by + c = 0, we get
a = 3, b = 4, c = -1
Let the given point A(x1, y1) = (1, 2)


Question 32.
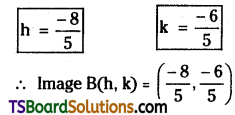
x – 3y – 5 = 0 is the perpendicular bisector of the line segment joining points A, B. If A = (-1, -3) find the coordinates of B. [Mar. ’13 (Old)]
Solution:
Given, equation of the straight line is x – 3y – 5 = 0
Comparing with ax + by + c = 0, we get
a = 1, b = -3, c = -5
Let the given point A(x1, y1) = (-1, -3)
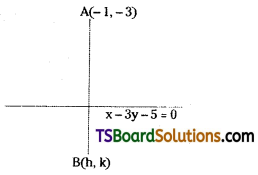
x – 3y – 5 = 0 is the perpendicular bisector of the line segment joining the points A, B then, B(h, k) is the image of A(-1, -3) with respect to the straight line x – 3y – 5 = 0.

Question 33.
If 2x – 3y – 5 = 0 is the perpendicular bisector of the line segment joining (3, -4) and (α, β), find α + β.
Solution:
Given, the equation of the straight line is 2x – 3y – 5 = 0
Comparing with ax + by + c = 0, we get
a = 2, b = -3, c = -5
Let the given point A(x1, y1) = (3, -4)
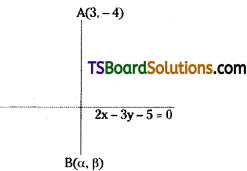
2x – 3y – 5 = 0 is the perpendicular bisector of the line segment joining the points A, B then, B(α, β) is the image of A(3, -4) with respect to the straight line 2x – 3y – 5 = 0.

∴ Image of A(3, 4) is (α, β) = (-1, 2)
∴ α + β = -1 + 2 = 1
Question 34.
Find the orthocentre of the triangle whose vertices are (-2, -1), (6, -1), and (2, 5). [May ’12; Mar. ’07, ’04]
Solution:
Let the given vertices are A(-2, -1), B(6, -1) & C(2, 5)



Question 35.
Find the orthocentre of the triangle whose vertices are (5, -2), (-1, 2), and (1, 4).
Solution:
Let the given points are A(5, -2), B(-1, 2) & C(1, 4)



![]()
Question 36.
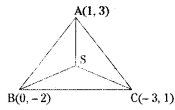
Find the circumcentre of the triangle whose vertices are (1, 3), (0, -2), and (-3, 1). [Mar. ’18 (AP); May ’06]
Solution:
Let A(1, 3), B(0, -2), C(-3, 1) are the given points.
Let S(α, β) be the circumcentre of the triangle ABC then, SA = SB = SC
Now, SA = SB
⇒ SA2 = SB2
⇒ (α – 1)2 + (β – 3)2 = (α – 0)2 + (β + 2)2
⇒ α2 – 2α + 1 + β2 + 9 – 6β = α2 + β2 + 4 + 4β
⇒ 4 + 4β + 2α – 9 + 6β – 1 = 0
⇒ 2α + 10β – 6 = 0
⇒ α + 5β – 3 = 0 ……(1)
Also SB = SC
⇒ SB2 = SC2
⇒ (α – 0)2 + (β + 2)2 = (α + 3)2 + (β – 1)2
⇒ α2 + β2 + 4 + 4β = α2 + 9 + 6α + β2 + 1 – 2β
⇒ 9 + 6α – 2β + 1 – 4 – 4β = 0
⇒ 6α – 6β + 6 = 0
⇒ α – β + 1 = 0 ………(2)
Solving (1) & (2)

Question 37.
Find the circumcentre of the triangle whose vertices are (1, 3), (-3, 5), and (5, -1). [Mar. ’18 (TS)]
Solution:
Let A(1, 3), B(-3, 5), C(5, -1) are the given points.
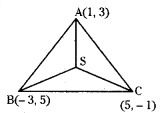
Let S(α, β) be the circumcentre of the triangle ABC then, SA = SB = SC
Now, SA = SB
⇒ SA2 = SB2
⇒ (α – 1)2 + (β – 3)2 = (α + 3)2 + (β – 5)2
⇒ α2 – 2α + 1 + β2 + 9 – 6β = α2 + 9 + 6α + β2 + 25 – 10β
⇒ 6α + 25 – 10β – 1 + 2α + 6β = 0
⇒ 8α – 4β + 24 = 0
⇒ 2α – β + 6 = 0 ……(1)
Also SB = SC
⇒ SB2 = SC2
⇒ (α + 3)2 + (β – 5)2 = (α – 5)2 + (β + 1)2
⇒ α2 + 9 + 6α + 25 + β2 – 10β = α2 + 25 – 10α + β2 + 1 + 2β
⇒ 9 + 6α – 10β + 10α – 1 – 2β = 0
⇒ 16α – 12β + 8 = 0
⇒ 4α – 3β + 2 = 0 ………(2)
Solving (1) & (2)
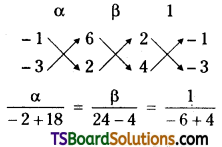
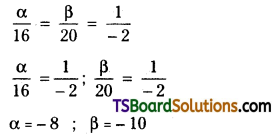
Circumcentre S = (-8, -10)
Question 38.
Find the circumcentre of the triangle whose vertices are (1, 0), (-1, 2), and (3, 2). [May ’13 (Old)]
Solution:
Let A(1, 0), B(-1, 2), C(3, 2) are the given points.
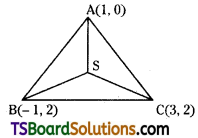
Let S(α, β) be the circumcentre of the triangle ABC then, SA = SB = SC
Now, SA = SB
⇒ SA2 = SB2
⇒ (α – 1)2 + (β – 0)2 = (α + 1)2 + (β – 2)2
⇒ α2 – 2α + 1 + β2 = α2 + 2α + 1 + β2 + 4 – 4β
⇒ 2α – 4β + 4 + 1 – 1 + 2α = 0
⇒ 4α – 4β + 4 = 0
⇒ α – β + 1 = 0 ……….(1)
Also SB = SC
⇒ SB2 = SC2
⇒ (α + 1)2 + (β – 2)2 = (α – 3)2 + (β – 2)2
⇒ α2 + 2α + 1 + β2 + 4 – 4β = α2 + 9 – 6α + β2 + 4 – 4β
⇒ 1 + 2α – 9 + 6α = 0
⇒ 8α – 8 = 0
⇒ α – 1 = 0
⇒ α = 1
Substitute α = 1 in (1), we get
1 – β + 1 = 0
⇒ -β = -2
⇒ β = 2
∴ Circumcentre S = (1, 2)
![]()
Question 39.
If the equations of the sides of a triangle are 7x + y – 10 = 0, x – 2y + 5 = 0, and x + y + 2 = 0, find the orthocenter of the triangle. [May ’09, ’00, ’97]
Solution:
Given, the equations of the straight lines are
7x + y – 10 = 0 …….(1)
x – 2y + 5 = 0 …….(2)
x + y + 2 = 0 ……….(3)
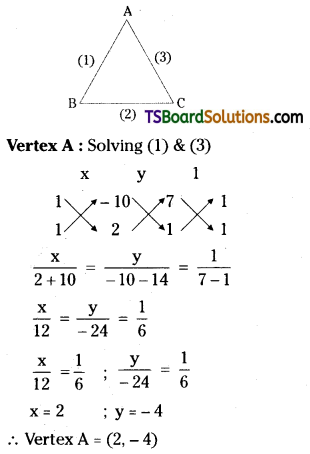

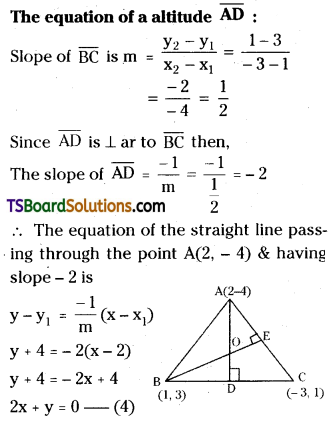

Question 40.
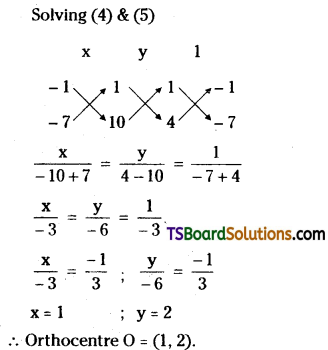
Find the orthocentre of the triangle whose sides are given by 4x – 7y + 10 = 0, x + y = 5, and 7x + 4y = 15.
Solution:
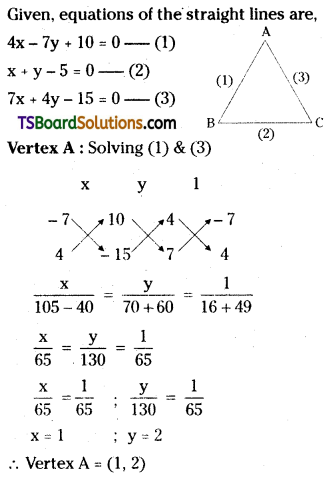




Question 41.
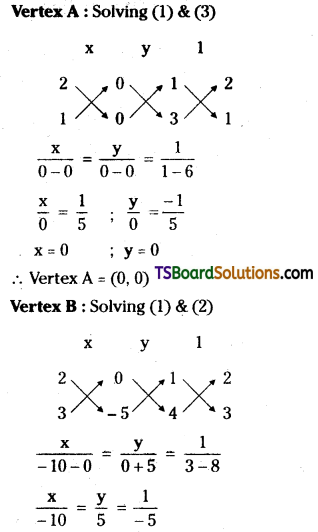
Find the orthocentre of the triangle formed by the lines x + 2y = 0, 4x + 3y – 5 = 0 and 3x + y = 0. [Mar. ’10]
Solution:
Given, the equations of the straight lines are,
x + 2y = 0 ……..(1)
4x + 3y – 5z = 0 ……….(2)
3x + y = 0 ………(3)


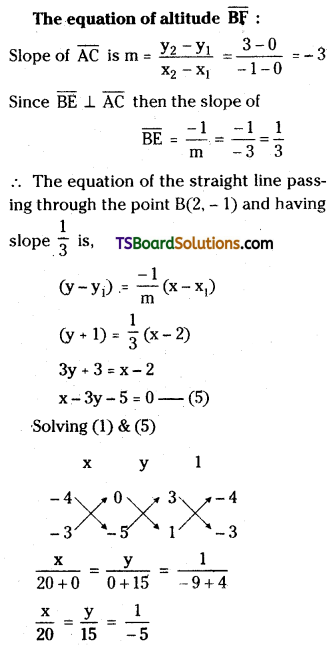
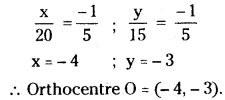
Question 42.
Find the circumcentre of the triangle formed by the straight lines x + y = 0, 2x + y + 5 = 0, and x – y = 2.
Solution:
Given, the equations of the straight lines are
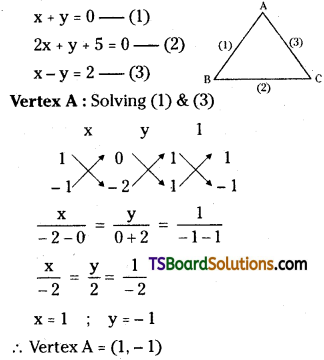

∴ Vertex C = (-1, -3)
Let S(α, β) be the circumcentre of the triangle then, SA = SB = SC
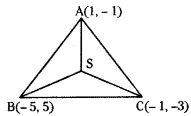
Now, SA = SB
⇒ SA2 = SB2
⇒ (α – 1)2 + (β + 1)2 = (α + 5)2 + (β – 5)2
⇒ α2 – 2α + 1 + β2 + 1 + 2β = α2 + 25 + 10α + β2 + 25 – 10β
⇒ 50 + 10α – 10β – 1 + 2α – 2β – 1 = 0
⇒ 12α – 12β + 48 = 0
⇒ α – β + 4 = 0 ……..(4)
Also SB = SC
⇒ SB2 = SC2
⇒ (α + 5)2 + (β – 5)2 = (α + 1)2 + (β + 3)2
⇒ α2 + 25 + 10α + β2 + 25 – 10β = α2 + 2α + 1 + β2 + 6β + 9
⇒ 25 + 25 + 10α – 10β – 1 = -2α – 9 – 6β = 0
⇒ 8α – 16β + 40 = 0
⇒ α – 2β + 5 = 0 ……..(5)
Solving (4) & (5)
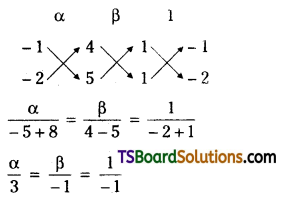
α = -3; β = 1
∴ Circumcentre S = (-3, 1)
![]()
Question 43.
Find the circumcentre of the triangle formed by the straight lines x + y + 2 = 0, 5x – y – 2 = 0, and x – 2y + 5 = 0. [May ’08]
Solution:
Given, the equations of the straight lines are
x + y + 2 = 0 ………(1)
5x – y – 2 = 0 ………(2)
x – 2y + 5 = 0 ………(3)
Let S(α, β) be the circumcentre of the triangle then, SA = SB = SC
Now, SA = SB
⇒ SA2 = SB2
⇒ (α + 3)2 + (β – 1)2 = (α – 0)2 + (β + 2)2
⇒ α2 + 9 + 6α + β2 + 1 – 2β = α2 + β2 + 4 + 4β
⇒ 6α – 2β + 9 + 1 – 4 – 4β = 0
⇒ 6α – 6β + 6 = 0
⇒ α – β + 1 = 0 ……..(4)
Also SB = SC
⇒ SB2 = SC2
⇒ (α + 0)2 + (β + 2)2 = (α – 1)2 + (β – 3)2
⇒ α2 + β2 + 4 + 4β = α2 – 2a + 1 + β2 – 6β + 9
⇒ 4 + 4β – 1 + 2α – 9 + 6β = 0
⇒ 2α + 10β – 6 = 0
⇒ α + 5β – 3 = 0 ……..(5)
Solving (4) & (5)

Question 44.
Find the equations of the straight lines passing through the point (-10, 4) and make an angle θ with the line x – 2y = 10 such that tan θ = 2.
Solution:
Given, equation of the straight line is x – 2y – 10 = 0 ……..(1)
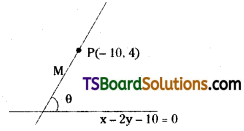
Let the given point P(x1, y1) = (-10, 4)
Given that, tan θ = 2
cos θ = \(\frac{1}{\sqrt{5}}\)
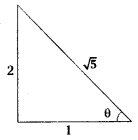
Let the slope of the required straight line = m.
∴ The equation of the straight line is passed through the point P(-10, 4) and having slope ‘m’ is y – y1 = m(x – x1)
y – 4 = m(x + 10)
y – 4 = mx + 10m
mx – y + 10m + 4 = 0
If ‘θ’ be the angle between the lines (1) & (2)

Squaring on both sides
5(m2 + 1) = 5(m + 2)2
5m2 + 5 = 5m2 + 20 + 20m (or) m = \(\frac{1}{0}\)
20m + 15 = 0
20m = -15
m = \(\frac{-3}{4}\) or m = \(\frac{1}{0}\)
Case 1: If m = \(\frac{-3}{4}\) then, the equation of the straight line is,
from (2), y – 4 = \(\frac{-3}{4}\) (x + 10)
4y – 16 = -3x – 30
3x + 4y – 16 + 30 = 0
3x + 4y + 14 = 0
Case 2: If m = \(\frac{1}{0}\) then, the equation of straight line is
from (2), y – 4 = \(\frac{1}{0}\) (x + 10)
0 = x + 10
x + 10 = 0
∴ Required equations of the straight lines are 3x + 4y + 10 = 0, x + 10 = 0
Question 45.
The base of an equilateral triangle is x + y – 2 = 0 and the opposite vertex is (2, -1). Find the equations of the remaining sides. [Mar. ’02]
Solution:
Given that base of an equilateral triangle is, x + y – 2 = 0 ……(1)
Let the opposite vertex is, A = (2, -1)
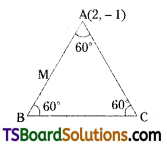
Since, Triangle ABC is an equilateral triangle B then,
A = B = C = 60°
Let the slope of the side \(\overline{\mathrm{AB}}\) = m
∴ The equation of the side \(\overline{\mathrm{AB}}\) passing through A(2, -1) and having slope ‘m’ is y – y1 = m(x – x1)
y + 1 = m(x – 2) ………(2)
y + 1 = mx – 2m
mx – y – 2m – 1 = 0
Let ‘θ’ be the angle between the lines (1) & (2) then,

∴ The equations of the required straight lines are
from (2), y + 1 = 2 ± √3(x – 2).
![]()
Question 46.
Prove that the points (1, 11), (2, 15), and (-3, -5) are collinear and find the equation of the straight line containing them.
Solution:
Let A(1, 11), B(2, 15), C(-3, -5) are the given points.
The equation of the straight line \(\overline{\mathrm{AB}}\) is,
(y – y1) (x2 – x1) = (x – x1)(y2 – y1)
⇒ (y – 11) (2 – 1) = (x – 1) (15 – 11)
⇒ (y – 11) (1) = (x – 1) (4)
⇒ y – 11 = 4x – 4
⇒ 4x – y + 7 = 0 ……….(1)
Now, substituting the point C(-3, -5) in equation (1)
4(-3) – (-5) + 7 = 0
⇒ -12 + 5 + 7 = 0
⇒ -7 + 7 = 0
⇒ 0 = 0
∴ The point C(-3, -5) lie on the straight line 4x – y + 7 = 0.
∴ Given points are collinear.
∴ The equation of the straight line is 4x – y + 7 = 0.
Question 47.
Find the angle which the straight line y = √3x – 4 makes with the Y-axis. [Mar. ’19 (AP & TS)]
Solution:
Given the equation of the straight line is y = √3x – 4
⇒ √3x – y – 4 = 0
Comparing the given equation with ax + by + c = 0, then
a = √3, b = -1, c = -4
The slope of a straight line √3x – y – 4 = 0 is
m = \(\frac{-a}{b}=\frac{-\sqrt{3}}{-1}\) = √3
tan θ = √3
∴ θ = 60° = \(\frac{\pi}{3}\)
The angle which the straight line y = √3x – 4 makes with X-axis = \(\frac{\pi}{3}\)
The angle which the straight line y = √3x – 4 makes with the Y-axis is = 180° – (90° + 60°)
= 180° – 150°
= 30°
= \(\frac{\pi}{6}\)
Question 48.
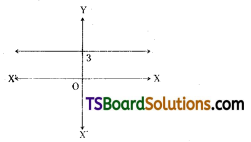
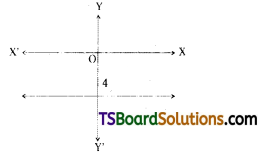
Write the equations of the straight lines parallel to the X-axis and (i) at a distance of 3 units above the X-axis and (ii) at a distance of 4 units below the X-axis.
Solution:
(i) The equation of the straight lines parallel to the X-axis, at a distance of 3 units above the X-axis is y = 3
(ii) The equation of the straight line parallel to the X-axis at a distance of 4 units below the X-axis is y = -4
Question 49.
Write the equations of the straight lines parallel to the Y-axis and (i) at a distance of 2 units from the Y-axis to the right of it (ii) at a distance of 5 units from the Y-axis to the left of it.
Solution:
(i) The equation of the straight line parallel to the Y-axis and at a distance of 2 units from the Y-axis to the right of it is x = 2.
(ii) The equation of the straight line parallel to the Y-axis and at a distance of 5 units from the Y-axis to the left of it is x = -5.
Question 50.
Find the equation of the straight line which makes an angle \(\frac{\pi}{4}\) with the positive X-axis in the positive direction and which passes through the point (0, 0).
Solution:
Given that, inclination of a straight line is θ = \(\frac{\pi}{4}\)
The slope of a line is m = tan θ
= tan \(\frac{\pi}{4}\)
= tan 45°
= 1
Let the given point A(x1, y1) = (0, 0)
∴ The equation of the straight line passing through A(0, 0) and having slope ‘1’ is y – y1 = m(x – x1)
⇒ y – o = 1(x – 0)
⇒ y = x – o
⇒ y = x
⇒ x – y = 0
![]()
Question 51.
Find the equation of the straight line which makes an angle of 135° with the positive X – axis in the positive direction and which pass through the point (3, -2).
Solution:
Given that, the inclination of a straight line is θ = 135°
The slope of a line is m = tan θ
= tan 135°
= tan (180° – 45°)
= tan 45°
= -1
Let the given point A(x1, y1) = (3, -2)
∴ The equation of the straight line passing through A(3, -2) and having slope ‘-1’ is y – y1 = m(x – x1)
⇒ y + 2 = -1(x – 3)
⇒ y + 2 = -x + 3
⇒ x + y + 2 – 3 = 0
⇒ x + y – 1 = 0
Question 52.
Find the equation of the straight line which makes an angle of 150° with the positive X-axis in the positive direction and the Y-intercept is 2.
Solution:
Given the inclination of a straight line is θ = 150°
The slope of a line is m = tan θ
= tan 150°
= -cot 60°
= \(\frac{-1}{\sqrt{3}}\)
y-intercept, c = 2.
The equation of the straight line having slope \(\frac{-1}{\sqrt{3}}\) and y-intercept ‘2’ is y = mx + c
⇒ y = \(\frac{-1}{\sqrt{3}}\)x + 2
⇒ y = \(\frac{-x+2 \sqrt{3}}{\sqrt{3}}\)
⇒ x + √3y – 2√3 = 0
Question 53.
Find the equation of the straight line which makes an angle \(\tan ^{-1}\left(\frac{2}{3}\right)\) with the positive X-axis in the positive direction and the y-intercept is 3.
Solution:
Given, inclination of a straight line is θ = \(\tan ^{-1}\left(\frac{2}{3}\right)\)
tan θ = \(\frac{2}{3}\)
Slope of a line is m = tan θ = \(\frac{2}{3}\)
y-intercept, c = 3
∴ The equation of a straight line having slope \(\frac{2}{3}\) and y-intercept ‘3’ is y = mx + c
⇒ y = \(\frac{2}{3}\) (x) + 3
⇒ y = \(\frac{2 x+9}{3}\)
⇒ 3y = 2x + 9
⇒ 2x – 3y + 9 = 0
Question 54.
Prove that the points (a, b + c), (b, c + a), (c, a + b) are collinear and find the equation of the straight line containing them.
Solution:
Let A(a, b + c), B(b , c + a), C(c, a + b) are the given points
The equation of the straight line \(\overline{\mathrm{AB}}\) is (y – y1) (x2 – x1) = (x – x1)(y2 – y1)
⇒ (y – b – c) (b – a) = (x – a) (c + a – b – c)
⇒ (y – b – c) (b – a) = (x – a) (a – b)
⇒ (y – b – c) (b – a) = -(x – a) (b – a)
⇒ y – b – c = -x + a
⇒ x + y – a – b – c = 0 ……..(1)
Now, Substituting the point C(c, a + b) in equation (1)
x + y – a – b – c = 0
⇒ c + a + b – a – b – c = o
⇒ 0 = 0
∴ Point C(c, a + b) lies on the straight line x + y – a – b – c = 0.
∴ Given points are collinear.
∴ The straight line equation is x + y – a – b – c = 0.
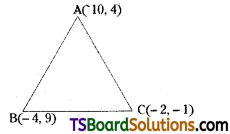
Question 55.
A(10, 4), B(-4, 9) and C(-2, -1) are the vertices of a triangle. Find the equations of (i) \(\overline{\mathrm{AB}}\) (ii) the median through A (iii) the altitude through B (iv) the perpendicular bisector of the side \(\overline{\mathrm{AB}}\).
Solution:
(i) Equation of the straight line \(\overline{\mathrm{AB}}\) is (y – y1) (x2 – x1)= (x – x1)(y2 – y1)
⇒ (y – 4)(-4 – 10) = (x – 10) (9 – 4)
⇒ (y – 4) (-14) = (x – 10) (5)
⇒ -14y + 56 = 5x – 50
⇒ 5x + 14y – 106 = 0
(ii) The equation of the median through ‘A’:
Since ‘D’ is the midpoint of BC, then
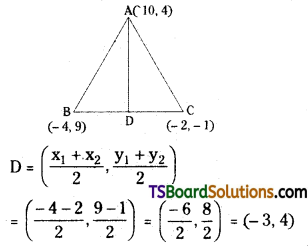
The equation of the median through A is the equation of the straight line \(\overline{\mathrm{AD}}\),
(y – y1)(x2 – x1) = (x – x1)(y2 – y1)
⇒ (y – 4) (-3 – 10) = (x – 10)(4 – 4)
⇒ (y – 4) (-13) = (x – 10)(0)
⇒ (y – 4)(-13) = 0
⇒ y – 4 = 0
(iii) The equation of the altitude through ‘B’:
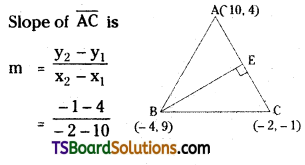
= \(\frac{5}{12}\)
Since \(\overline{\mathrm{BE}} \perp \overline{\mathrm{AC}}\), then
slope of \(\overline{\mathrm{BE}}\) = \(\frac{-1}{m}=\frac{-1}{\frac{5}{12}}=\frac{-12}{5}\)
The equation of the altitude through B is, the equation of the straight line passing through B(-4, 9) and having slope \(\frac{-12}{5}\) is y – y1 = m(x – x1)
⇒ y – 9 = \(\frac{-12}{5}\) (x + 4)
⇒ 5y – 45 = -12x – 48
⇒ 12x + 5y + 3 = 0
(iv) The equation of the perpendicular bisector of side \(\overline{\mathrm{AB}}\):

∴ The equation of the perpendicular bisector of \(\overline{\mathrm{AB}}\) is, the equation of the straight line passing through F(3, \(\frac{13}{2}\)) and having slope \(\frac{14}{5}\) is y – y1 = m(x – x1)
⇒ y – \(\frac{13}{2}\) = \(\frac{14}{5}\)(x – 3)
⇒ \(\frac{2 y-13}{2}=\frac{14}{5}(x-3)\)
⇒ 10y – 65 = 28x – 84
⇒ 28x – 10y – 19 = 0
![]()
Question 56.
A straight line passing through A(1, -2) makes an angle \(\tan ^{-1}\left(\frac{4}{3}\right)\) with the positive direction of the X-axis in the anti-clockwise sense. Find the points on the straight line whose distance from A is 5.
Solution:
Given point (x1, y1) = A(1, -2)
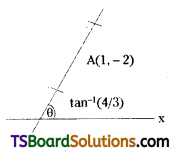
The inclination of the straight line is θ = \(\tan ^{-1}\left(\frac{4}{3}\right)\)
tan θ = \(\frac{4}{3}\)
sin θ = \(\frac{4}{5}\)
cos θ = \(\frac{3}{5}\)
Distance, |r| = 5 units
Required point = (x1 + |r| cos θ, y1 + |r| sin θ)
= (x1 ± r cos θ, y1 ± r sin θ)
= (1 ± 5 . \(\frac{3}{5}\), -2 ± 5 . \(\frac{4}{5}\))
= (1 ± 3, -2 ± 4)
= (1 + 3, (-2) + 4), (1 – 3, -2 – 4)
= (4, 2), (-2, -6)
Question 57.
Find the sum of the squares of the intercepts of the line 4x – 3y = 12 on the axes of coordinates. [Mar. ’18 (AP)]
Solution:
Given, the equation of the straight line is 4x – 3y = 12
\(\frac{x}{3}+\frac{y}{-4}=1\) which is of the form \(\frac{x}{a}+\frac{y}{b}=1\)
∴ x-intercept, a = 3, y-intercept, b = -4
Now, the Sum of the squares of the intercepts = a2 + b2
= 32 + (-4)2
= 9 + 16
= 25
Question 58.
The intercepts of a straight line on the axes of coordinates are a and b. If p is the length of the perpendicular drawn from the origin to this line, write the value of p in terms of a and b.
Solution:
The intercepts of a straight line on the coordinate axes are a, b.
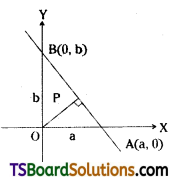

This is of the form x cos α + y sin α = p
∴ p = the length of the perpendicular drawn from the origin to the line = \(\frac{|a b|}{\sqrt{a^2+b^2}}\)
Question 59.
If the product of the intercepts made by the straight line x tan α + y sec α = 1 (0 ≤ α ≤ \(\frac{\pi}{2}\)) on the coordinate axes is equal to sin α, find α.
Solution:
Given, the equation of the straight line is x tan α + y sec α = 1
\(\frac{x}{\frac{1}{\tan \alpha}}+\frac{y}{\frac{1}{\sec \alpha}}=1\)
\(\frac{x}{\cot \alpha}+\frac{y}{\cos \alpha}=1\)
This is of the form \(\frac{x}{a}+\frac{y}{b}=1\)
∴ x-intercept (a) = cot α
y-intercept (b) = cos α
Given that, a product of the intercepts is equal to sin α.
cot α × cos α = sin α
⇒ \(\frac{\cos \alpha}{\sin \alpha}\) × cos α = sin α
⇒ \(\frac{\cos ^2 \alpha}{\sin ^2 \alpha}\) = 1
⇒ cot2α = 1
⇒ tan2α = 1
⇒ tan α = 1
⇒ α = \(\frac{\pi}{2}\) (∵ 0 ≤ α ≤ \(\frac{\pi}{2}\))
Question 60.
A straight line passing through A(-2, 1) makes an angle of 30° with \(\overline{\mathrm{OX}}\) in the positive direction. Find the points on the straight line whose distance from A is 4 units.
Solution:
Given point A(x1, y1) = (-2, 1)
Inclination of straight line = 30°
distance |r| = 4
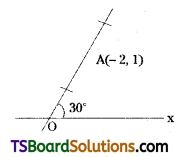
∴ Required points = (x1 + |r| cos θ, y1 + |r| sin θ)
= (x1 ± r cos θ, y1 ± r sin θ)
= (-2 ± 4 cos 30°, 1 ± 4 sin 30°)
= (-2 ± 4\(\left(\frac{\sqrt{3}}{2}\right)\), 1 ± 4(\(\frac{1}{2}\)))
= (-2 ± 2√3 ,1 ± 2)
= (-2 + 2√3, 1 + 2), (-2 – 2√3, +1 – 2)
= (-2 + 2√3, 3), (-2 + 2√3, -1)
Question 61.
A straight line whose inclination with the positive direction of the X-axis measured in the anti-clockwise sense is \(\frac{\pi}{3}\) makes a positive intercept on the Y-axis. If the straight line is at a distance of 4 from the origin; find its equation.
Solution:
Given that, inclination of a straight line is θ = \(\frac{\pi}{3}\)
Let ‘l’ is the required straight line.
Now, ‘N’ is the foot of the perpendicular from the origin to the straight line ‘L’
∴ ∠XON = 150°
∴ a = 150°
Given that, p = 4
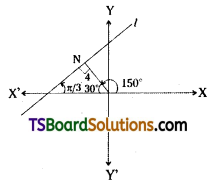
The equation of the straight line ‘L’ in the normal form is x cos α + y sin α = p
⇒ x cos (150°) + y sin (150°) = 4
⇒ x cos(180 – 30) + y sin (180 – 30) = 4
⇒ -x cos 30° + y sin 30° = 4
⇒ \(-x\left(\frac{\sqrt{3}}{2}\right)+y\left(\frac{1}{2}\right)=4\)
⇒ -√3x + y = 8
⇒ √3x – y + 8 = 0
![]()
Question 62.
Find the ratio in which the straight line 2x + 3y – 10 = 0 divides the join of the points (2, 3) and (2, 10).
Solution:
Given equation of the straight line is L = 2x + 3y – 10 = 0
Comparing the equation with ax + by + c = 0, we get
a = 2, b = 3, c = -10
Let the given points are A(x1, y1) = (2, 3) and B(x2, y2) = (2, 10)

Question 63.
State whether (3, 2) and (-4, -3) are on the same side or opposite sides of the straight line 2x – 3y + 4 = 0.
Solution:
Given equation of the straight line is L = 2x – 3y + 4 = 0
Let the given points are A(x1, y1) = (3, 2) and B(x2, y2) = (-4, -3)
Now, l11 = L(3, 2)
= 2(3) – 3(2) + 4
= 6 – 6 + 4
= 4 > 0
l22 = L(-4, -3)
= 2(-4) – 3(-3) + 4
= -8 + 9 + 4
= 5 > 0
Since l11 0 and l22 > 0, the given points are on the same side of the straight line, L = 0.
Question 64.
Find the ratio’s in which (i) the X-axis and (ii) the Y-axis divide the line segment \(\overline{\mathrm{AB}}\) joining A(2, -3) and B(3, -6).
Solution:
Given points are A(x1, y1) = (2, -3) and B(x2, y2) = (3, -6)
(i) The X-axis divides the line segment AB in the ratio is,
-y1 : y2 = -(-3) : -6
= 3 : -6
= 1 : -2
= -1 : 2
(ii) Y-axis divides \(\overline{\mathrm{AB}}\) in the ratio is,
-x1 : x2 = -2 : 3
Question 65.
Find the equation of the straight line passing through the point of intersection of the lines x + y + 1 = 0 and 2x – y + 5 = 0 and containing the point (5, -2).
Solution:
Given, the equations of the straight lines are
x + y + 1 = 0 ……….(1)
2x – y + 5 = 0 ………..(2)
Let the given point be (5, -2)
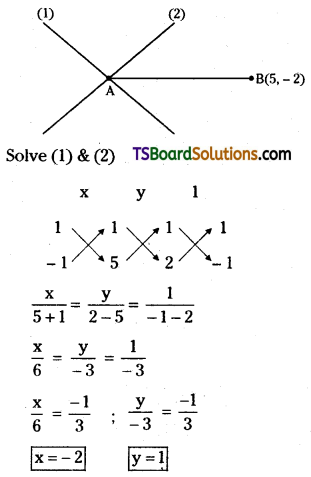
∴ The point of intersection of lines (1) & (2) is A = (-2, 1)
Now, the equation of the straight line \(\overline{\mathrm{AB}}\) is (y – y1)(x2 – x1) = (x – x1)(y2 – y1)
⇒ (y – 1) (5 + 2) = (x + 2) (-2 – 1)
⇒ (y – 1)(7) = (x + 2)(-3)
⇒ 7y – 7 = -3x – 6
⇒ 3x + 7y – 1 = 0
Question 66.
Find the ratio in which the straight line 3x + 4y = 6 divides the join of the points (2, -1) and (1, 1).
Solution:
Given equation of the straight line is L = 3x + 4y – 6 = 0
Comparing the equation with ax + by + c = 0, we get
a = 3, b = 4, c = -6
Let the given points are A(x1, y1) = (2, -1) and B(x2, y2) = (1, 1)
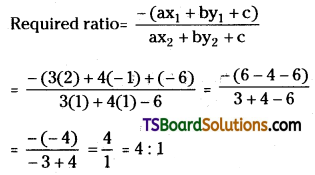
Question 67.
Transform the equation (2 + 5k)x – 3(1 + 2k)y + (2 – k) = 0 into the form L1 + λL2 = 0 and find the point of concurrency of the family of straight lines represented by the equation.
Solution:
Given, equation is (2 + 5k)x – 3(1 + 2k)y + (2 – k) = 0
⇒ 2x + 5kx – 3y – 6ky + 2 – k = 0
⇒ (2x – 3y + 2) + k(5x – 6y – 1) = 0
This is of the form l1 + λl2 = 0
where l1 = 2x – 3y + 2 = 0 ……..(1)
l2 = 5x – 6y – 1 = 0 ……..(2)
Solving (1) & (2)
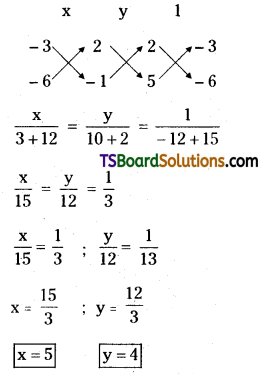
∴ Point of concurrence = (5, 4)
![]()
Question 68.
Transform the equation (k + 1)x + (k + 2)y + 5 = 0, into the form L1 + λL2 = 0 and find the point of concurrency of the family of straight lines represented by the equation.
Solution:
Given, equation is (k + 1)x + (k + 2)y + 5 = 0
⇒ kx + x + ky + 2y + 5 = 0
⇒ (x + 2y + 5) + k(x + y) = 0
This is of the form l1 + λl2 = 0
where l1 = x + 2y + 5 = 0 ………(1)
l2 = x + y = 0 ……..(2)
Solving (1) & (2)
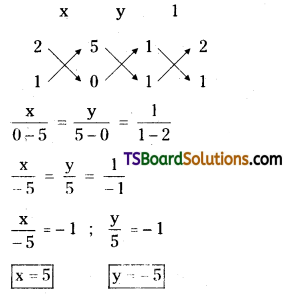
∴ Point of concurrence = (5, -5)
Question 69.
Find the area of the triangle formed by the straight line x – 4y + 2 = 0 and the coordinate axes.
Solution:
Given, equation of the straight line is x – 4y + 2 = 0 ………(1)
Comparing with ax + by + c = 0, we get
a = 1, b = -4, c = 2
∴ The area of the triangle formed by the straight line (1) & the co-ordinate axis = \(\frac{c^2}{2|a b|}=\frac{2^2}{2|1(-4)|}\) = \(\frac{1}{2}\)
Question 70.
Find the area of the triangle formed by the straight line 3x – 4y + 12 = 0 and the coordinate axes.
Solution:
Given, equation of the straight line is 3x – 4y + 12 = 0 ………(1)
Comparing with ax + by + c = 0, we get
a = 3, b = -4, c = 12
∴ The area of the triangle formed by the straight line and the co-ordinate axis = \(\frac{c^2}{2|a b|}=\frac{12^2}{2|3(-4)|}=\frac{12^2}{2|-12|}=\frac{144}{2(12)}\)
= 6 sq. units.
Question 71.
Find the equation of the straight line passing through the points (-1, 2) and (5, -1) and the area of the triangle formed by it with the axes of coordinates. [May ’15 (TS)]
Solution:
Let the given points are A(x1, y1) = (-1, 2) & B(x2, y2) = (5, -1)
The equation of the straight line passing through the points A(-1, 2) & B(5, -1) is (y – y1)(x2 – x1) = (x – x1)(y2 – y1)
⇒ (y – 2) (5 + 1) = (x + 1) (-1 – 2)
⇒ (y – 2)(6) = (x + 1)(-3)
⇒ 2y – 4 = -x – 1
⇒ x + 2y – 3 = 0 ……..(1)
Comparing equation (1) with ax + by + c = 0, we get
a = 1, b = 2, c = -3
∴ The area of the triangle formed by the straight line (1) and the co-ordinate axis = \(\frac{c^2}{2|a b|}=\frac{9}{2|1(2)|}=\frac{9}{2(2)}=\frac{9}{4}\) sq. units
Question 72.
Find the set of values of ‘a’ if the points (1, 2) and (3, 4) lie to the same side of the straight line 3x – 5y + a = 0.
Solution:
Given, equation of the straight line is 3x – 5y + a = 0 ……..(1)
Comparing (1) with ax + by + c = 0, we get
a = 3, b = -5, c = a
Let the given points are A(x1, y1) = (1, 2) & B(x2, y2) = (3, 4)
Given that, the points (1, 2) & (3, 4) lie on the same direction 3x – 5y + a = 0, then -l11 : l22 < 0
⇒ \(\frac{-\mathrm{L}_{11}}{\mathrm{~L}_{22}}\) < 0
⇒ \(\frac{-\left(a x_1+b y_1+c\right)}{\left(a x_2+b y_2+c\right)}\) < 0

Question 73.
Find the angle between the lines 2x + y + 4 = 0 and y – 3x = 7.
Solution:
Given, the equation of the straight lines is
2x + y + 4 = 0 ……..(1)
y – 3x – 7 = 0
⇒ 3x – y + 7 = 0 …….(2)
Comparing (1) with a1x + b1y + c1 = 0, we get
a1 = 2, b1 = 1, c1 = 4
Comparing (2) with a2x + b2y + c2 = 0, we get
a2 = 3, b2 = -1, c2 = 7
If ‘θ’ is the angle between the lines (1) & (2)
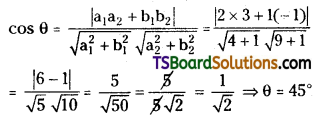
Question 74.
Find the angle between the lines √3x + y + 1 = 0 and x + 1 = 0.
Solution:
Given, the equation of the straight lines are
√3x + y + 1 = 0 …….(1)
x + 1 = 0 ………(2)
Comparing (1) with a1x + b1y + c1 = 0, we get
a1 = √3, b1 = 1, c1 = 1
Comparing (2) with a2x + b2y + c2 = 0, we get
a2 = 1, b2 = 0, c2 = 1
If ‘θ’ is the angle between the lines (1) & (2)

![]()
Question 75.
Find the angle between the lines ax + by = a + b, a(x – y) + b(x + y) = 2b.
Solution:
Given, the equation of the straight lines are
ax + by = a + b
ax + by – a – b = 0 …….(1)
a(x – y) + b(x + y) = 2b
ax – ay + bx + by = 2b
(a + b)x + (-a + b)y – 2b = 0 ………(2)
Comparing (1) with a1x + b1y + c1 = 0, we get
a1 = a, b1 = b, c1 = -a – b
Comparing (2) with a2x + b2y + c2 = 0, we get
a2 = a + b, b2 = b – a, c2 = -2b
If ‘θ’ is the angle between the lines (1) & (2)

Question 76.
Find the equation of a straight line perpendicular to the line 5x – 3y + 1 = 0 and pass through the point (4, -3). [Mar. ’15 (TS)]
Solution:
Given, the equation of the straight line is 5x – 3y + 1 = 0
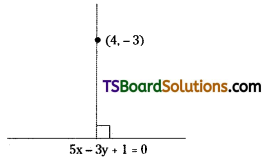
Slope of the given line is m = \(\frac{-5}{-3}=\frac{5}{3}\)
Slope of the perpendicular line = \(\frac{-1}{m}=\frac{-1}{\frac{5}{3}}=\frac{-3}{5}\)
Let the given point A(x1, y1) = (4, -3)
Equation of the straight line passing through (4, -3) and having slope \(\frac{-3}{5}\) is,
y – y1 = \(\frac{-1}{m}\)(x – x1)
⇒ y + 3 = \(\frac{-3}{5}\)(x – 4)
⇒ 5y + 15 = -3x + 12
⇒ 3x + 5y + 3 = 0
Question 77.
Find the value of k, if the straight line 6x – 10y + 3 = 0 and kx – 5y + 8 = 0 are parallel.
Solution:
Given, the equation of the straight line is
6x – 10y + 3 = 0 …….(1)
kx – 5y + 8 = 0 ……(2)
Slope of the line (1) is m1 = \(\frac{-a}{b}=\frac{-6}{-10}=\frac{3}{5}\)
Slope of the line (2) is m2 = \(\frac{-k}{-5}=\frac{k}{5}\)
Since the given lines are parallel then m1 = m2
⇒ \(\frac{3}{5}\) = \(\frac{k}{5}\)
⇒ k = 3
Question 78.
(-4, 5) is a vertex of a square and one of its diagonals is 7x – y + 8 = 0. Find the equation of the other diagonal.
Solution:
Let ABCD be a square.
Let the given point be A(-4, 5).
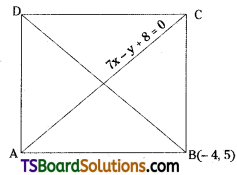
Equation of the diagonal \(\overline{\mathrm{AC}}\) is, 7x – y + 8 = 0 is given
Slope of the diagonal, \(\overline{\mathrm{AC}}\) = 7
Since in a square diagonals \(\overline{\mathrm{AC}}\) & \(\overline{\mathrm{BD}}\) are perpendicular
then slope of the diagonal \(\overline{\mathrm{BD}}\) = \(\frac{-1}{m}=\frac{-1}{7}\)
∴ The equation of the diagonal \(\overline{\mathrm{BD}}\) is y – y1 = \(\frac{-1}{m}\)(x – x1)
⇒ y – 5 = \(\frac{-1}{7}\)(x + 4)
⇒ 7y – 35 = -x – 4
⇒ x + 7y – 31 = 0
Question 79.
A(-1, 1), B(5, 3) are opposite vertices of a square in the XY plane. Find the equation of the other diagonal (not passing through A, B) of the square.
Solution:
Let ABCD be a square.
Given that, opposite vertices of a square are A(-1, 1) and B(5, 3).
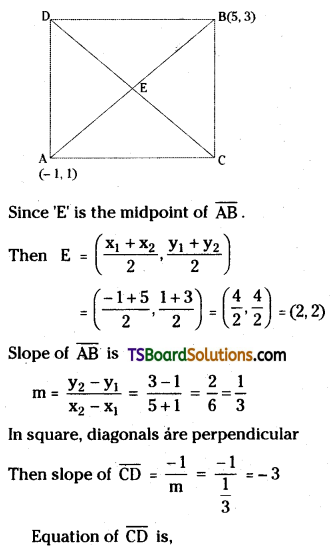
The equation of straight line passing through E & slope -3 is y – y1 = \(\frac{-1}{m}\)(x – x1)
⇒ y – 2 = -3(x – 2)
⇒ y – 2 = -3x + 6
⇒ 3x + y – 8 = 0
![]()
Question 80.
Show that lines x – 7y – 22 = 0, 3x + 4y + 9 = 0 and 7x + y – 54 = 0 form a right angled isosceles triangle.
Solution:
Given, the equations of the straight lines are
x – 7y – 22 = 0 …..(1)
3x + 4y + 9 = 0 …….(2)
7x + y – 54 = 0 ………(3)
Let ‘A’ be the angle between the lines (1) & (3) then,

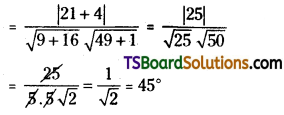
∴ A = 90°, B = 45°, C = 45°
∴ Given lines form a right angle isosceles triangle.
Question 81.
If ab > 0, find the area of the rhombus enclosed by the four straight lines ax ± by ± c = 0.
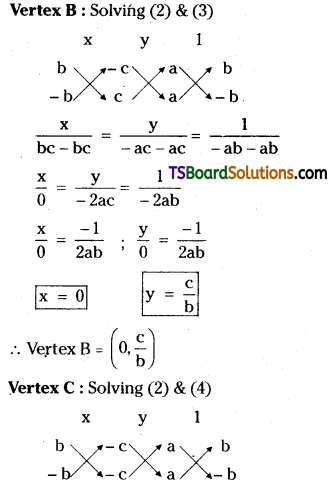
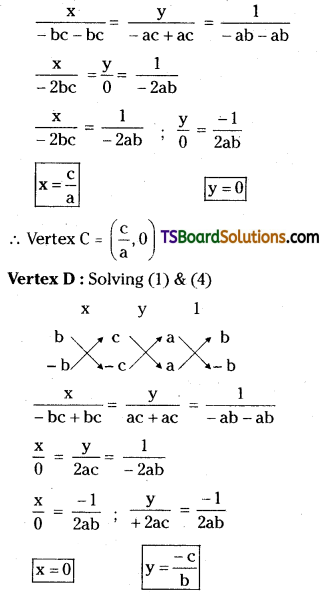
Solution:
Given, the equations of the straight lines are
ax + by + c = 0 ……..(1)
ax + by – c = 0 ………(2)
ax – by + c = 0 ……..(3)
ax – by – c = 0 ………(4)
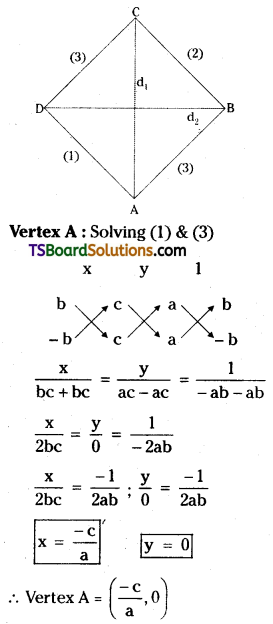
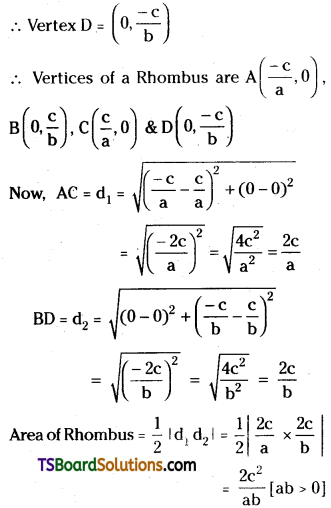
Question 82.
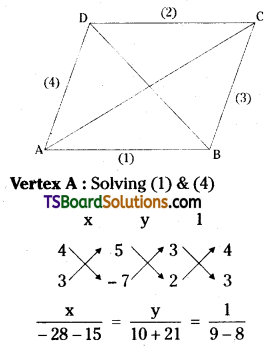
Find the area of the parallelogram whose sides are 3x + 4y + 5 = 0, 3x + 4y – 2 = 0, 2x + 3y + 1 = 0 and 2x + 3y – 7 = 0.
Solution:
Given, the equations of the straight lines are
3x + 4y + 5 = 0 …….(1)
3x + 4y – 2 = 0 ………(2)
2x + 3y + 1 = 0 ……….(3)
2x + 3y – 7 = 0 ………..(4)



Question 83.
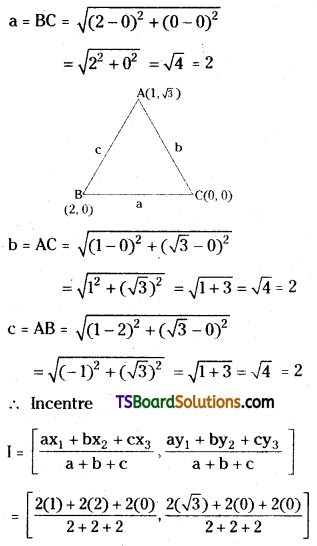
Find the incentre of the triangle whose vertices are (1, √3), (2, 0), and (0, 0).
Solution:
Given, A (x1, y1) = (1, √3), B(x2, y2) = (2, 0), C(x3, y3) = (0, 0)
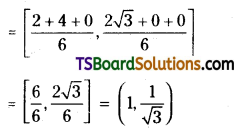
Question 84.
Find the incentre of the triangle whose sides are x = 1, y = 1, and x + y = 1.
Solution:
Given, the equation of the straight lines are
x = 1 …….(1)
y = 1 ………(2)
x + y = 1 ……..(3)
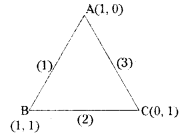
Vertex A:
Solving (1) & (3)
from (1), x = 1
from (3), x + y = 1
⇒ 1 + y = 1
⇒ y = 0
∴ Vertex A = (1, 0)
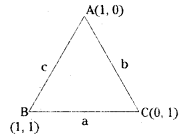
Vertex B:
Solving (1) & (2)
from (1), x = 1
from (2), y = 1
∴ Vertex B = (1, 1)
Vertex C:
Solving (2) & (3)
from (2), y = 1
from (3), x + y = 1
⇒ x + 1 = 1
⇒ x = 0
∴ Vertex C = (0, 1)


![]()
Question 85.
Find the values of k, if the angle between the straight lines kx + y + 9 = 0 and 3x – y + 4 = 0 is \(\frac{\pi}{4}\).
Solution:
Given equations are
kx + y + 9 = 0 ……..(1)
3x – y + 4 = 0 ………(2)
Comparing (1) with a1x + b1y + c1 = 0, we get
a1 = k, b1 = 1, c1 = 9
Comparing (2) with a2x + b2y + c2 = 0, we get
a2 = 3, b2 = -1, c2 = 4
Given that, θ = \(\frac{\pi}{4}\)
Let ‘θ’ is the angle between the lines (1) & (2) then


Squaring on both sides
⇒ (k2 + 1)(10) = 2(3k – 1)2
⇒ 10k2 + 10 = 18k2 + 2 – 12k
⇒ 8k2 – 12k – 8 = 0
⇒ 2k2 – 3k – 2 = 0
⇒ 2k2 – 4k + k – 2 = 0
⇒ (k – 2)(2k + 1) = 0
⇒ k = 2 or k = \(\frac{-1}{2}\)
Question 86.
Find the equation of the straight line passing through the origin and also through the point of intersection of the lines 2x – y + 5 = 0 and x + y + 1 = 0.
Solution:
Given equations of the straight lines are
2x – y + 5 = 0 ………(1)
x + y + 1 = 0 ………(2)
Solving (1) & (2)

The point of intersection of lines (1) & (2) is P(-2, 1).
The equation of the straight line passing through the point O(0, 0) & P(-2, 1) is (y – y1)(x2 – x1) = (x – x1)(y2 – y1)
⇒ (y – 0) (-2 – 0) = (x – 0) (1 – 0)
⇒ -2y = x
⇒ x + 2y = 0
Question 87.
Find the equation of the straight line perpendicular to the line 2x + 3y = 0 and pass through the point of intersection of the lines x + 3y – 1 = 0 and x – 2y + 4 = 0.
Solution:
Given equations of the straight lines are
x + 3y – 1 = 0 ……..(1)
x – 2y + 4 = 0 …….(2)
Solving (1) & (2)

∴ The point of intersection of lines (1) & (2) is P(-2, 1).
Given equation of the straight line 2x + 3y = 0 ……..(3)
Slope of line is m = \(\frac{-2}{3}\)
Since the required line is perpendicular to the line (3),
Slope of required line is \(\frac{-1}{m}=\frac{-1}{\frac{-2}{3}}=\frac{3}{2}\)
The equation of the straight line passing through P(-2, 1) & slope \(\frac{3}{2}\) is y – y1 = \(\frac{-1}{m}\) (x – x1)
⇒ y – 1 = \(\frac{3}{2}\) (x + 2)
⇒ 2y – 2 = 3x + 6
⇒ 3x – 2y + 8 = 0
![]()
Question 88.
Find the value of ‘a’ if the distances of the points (2, 3) and (-4, a) from the straight line 3x + 4y – 8 = 0 are equal.
Solution:
Given the equation of the straight line is 3x + 4y – 8 = 0
Let the given points be P = (2, 3), Q (-4, a)
Now, the perpendicular distance from the point P(2, 3) to the straight line 3x + 4y – 8 = 0 is

The perpendicular distance from the point Q(-4, a) to the straight line 3x + 4y – 8 = 0 is,

Given that two perpendicular distances are equal then,
2 = \(\frac{|4 a-20|}{5}\)
⇒ |4a – 20| = 10
⇒ 2|2a – 10| = 10
⇒ 2a – 10 = ±5
⇒ 2a – 10 = 5; 2a – 10 = -5
⇒ 2a = 15; 2a = 5
⇒ a = \(\frac{15}{2}\); a = \(\frac{5}{2}\)
∴ a = \(\frac{15}{2}\) (or) \(\frac{5}{2}\)
Question 89.
Two adjacent sides of a parallelogram are given by 4x + 5y = 0 and 7x + 2y = 0 and one diagonal is 11x + 7y = 9. Find the equations of the remaining sides and the other diagonal.
Solution:
Given that, two adjacent sides of a parallelogram are given by
4x + 5y = 0 …….(1)
7x + 2y = 0 ………(2)
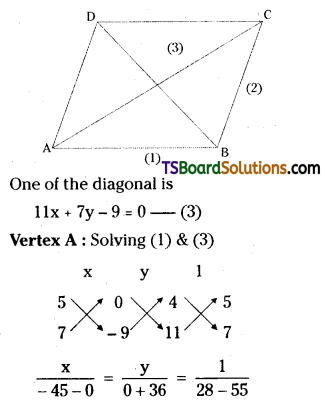

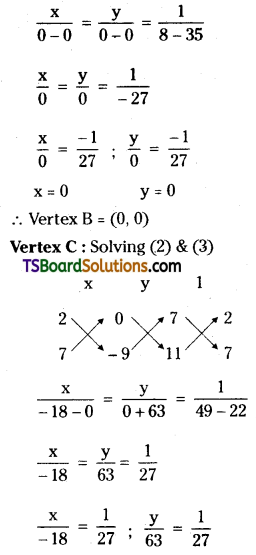


⇒ -6y – 8 = 21x – 35
⇒ 21x + 6y – 27 = 0
⇒ 7x + 2y – 9 = 0
The equation of the diagonal \(\overline{\mathrm{BD}}\) is,
(y – y1)(x2 – x1) = (x – x1)(y2 – y1)
⇒ (y – 0)(1 – 0) = (x – 0)(1 – 0)
⇒ y(1) = x(1)
⇒ y = x
⇒ x – y = 0
∴ Two adjacent sides of a parallelogram are 4x + 5y – 9 = 0, 7x + 2y – 9 = 0.
The equation of one of the diagonals is x – y = 0.
Question 90.
Find the incentre of the triangle formed by the straight lines x + 1 = 0, 3x – 4y = 5, and 5x + 12y = 27.
Solution:
Given, the equation of the straight lines are
x + 1 = 0 ………(1)
3x – 4y = 5 ………..(2)
5x + 12y = 27 ………..(3)
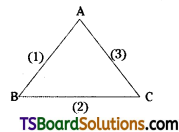
Vertex A:
Solving (1) & (3)
from (1), x + 1 = 0
⇒ x = -1
from (3), 5(-1) + 12y = 27
⇒ -5 + 12y = 27
⇒ 12y = 32
⇒ y = \(\frac{32}{12}\) = \(\frac{8}{3}\)
∴ Vertex A = (-1, \(\frac{8}{3}\))
Vertex B:
Solving (1) & (2)
from (1), x + 1 = 0
⇒ x = -1
from (2), 3(-1) – 4y = 5
⇒ -3 – 4y = 5
⇒ -4y = 8
⇒ y = -2
∴ Vertex B = (-1, -2)
Vertex C:
Solving (2) & (3)
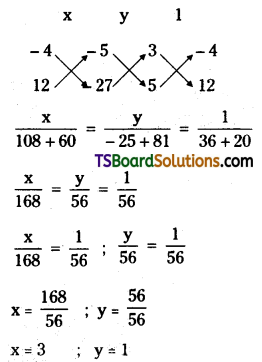


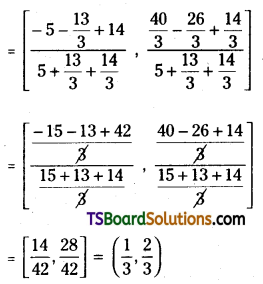
Question 91.
Find the equation of the straight line parallel to the line 3x + 4y = 7 and passing through the point of intersecting of the lines x – 2y – 3 = 0, x + 3y – 6 = 0. [Mar. ’16 (TS)]
Solution:
Given, the equation of the straight lines are
x – 2y – 3 = 0 …….(1)
x – 3y – 6 = 0 …….(2)
Solving (1) & (3)
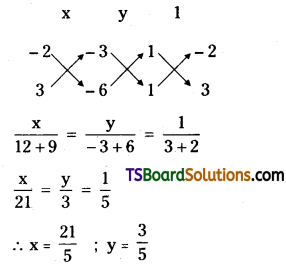
∴ The point of intersection of lines (1) & (2) is \(\mathrm{P}\left(\frac{21}{5}, \frac{3}{5}\right)\)
Given equation of the straight line is 3x + 4y = 7 …….(3)
Slope of line is m = \(\frac{-3}{4}\)
Since the required line is parallel to line 3.
Slope of required line = m = \(\frac{-3}{4}\)
∴ The equation of the straight line passing through \(\mathrm{P}\left(\frac{21}{5}, \frac{3}{5}\right)\) & Slope = \(\frac{-3}{4}\) is y – y1 = m(x – x1)
⇒ \(y-\frac{-3}{5}=\frac{-3}{4}\left(x-\frac{21}{5}\right)\)
⇒ \(\frac{5 y-3}{5}=\frac{-3}{4}\left(\frac{5 x-21}{5}\right)\)
⇒ 5y – 3 = \(\frac{-3}{4}\)(5x – 21)
⇒ 20y – 12 = -15x + 63
⇒ 15x + 20y – 75 = 0
⇒ 3x + 4y – 15 = 0
![]()
Question 92.
Find the value of p, if the straight lines 3x + py – 1 = 0, 7x – 3y + 3 = 0, are mutually perpendicular. [Mar. ’19 (TS)]
Solution:
Given lines are
3x + py – 1 = 0 ……..(1)
7x – 3y + 3 = 0 ………(2)
Slope of (1) is m1 = \(\frac{-3}{p}\)
Slope of (2) is m2 = \(\frac{-7}{-3}\) = \(\frac{7}{3}\)
Since (1) & (2) are perpendicular then
m1 × m2 = -1
⇒ \(\frac{-3}{p} \times \frac{7}{3}=-1\)
⇒ \(\frac{-7}{p}\) = -1
⇒ p = 7