TS Inter 1st Year Physics Study Material Chapter 3 సరళరేఖాత్మక గమనం

Telangana TSBIE TS Inter 1st Year Physics Study Material 3rd Lesson సరళరేఖాత్మక గమనం Textbook Questions and Answers.

TS Inter 1st Year Physics Study Material 3rd Lesson సరళరేఖాత్మక గమనం

అతిస్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
గమన, నిశ్చల స్థితులు సాపేక్షం. వివరించండి.
జవాబు:
పరిసరాలతో పోల్చినపుడు వస్తువు స్థానం కాలంతోపాటు మారితే అది గమనంలో ఉన్నది అంటారు. దాని స్థానం మారకపోతే ఆ వస్తువు నిశ్చలంగా ఉంది అంటారు. కాబట్టి గమనము లేదా నిశ్చలత్వము అనేది సాపేక్ష భావన మాత్రమే!

ప్రశ్న 2.
సగటు వేగం ఏవిధంగా తత్కాల వేగంతో విభేదిస్తుంది?
జవాబు:
సగటు వేగము వస్తువు యొక్క మొత్తము స్థానభ్రంశము మరియు మొత్తం కాలవ్యవధుల నిష్పత్తి. తత్కాల వేగము ఇచ్చిన క్షణంలో వస్తువుకు గల వేగము. మొత్తం కాలవ్యవధిని At వ్యవధి గల చిన్న చిన్న అంశాలుగా భావించి ఆ కాలాలలో గల తత్కాల వేగాల మొత్తమునకు, మొత్తం కాలమునకు గల నిష్పత్తిని సగటు వేగంగా భావిస్తారు. అనగా కొన్ని క్షణాలలో తత్కాల వేగం సగటు వేగం కన్నా ఎక్కువగా లేక తక్కువగా ఉండే అవకాశం ఉంది.

ప్రశ్న 3.
ఒక వస్తువు వేగం శూన్యమై దాని త్వరణం శూన్యం కాని సందర్భానికి ఒక ఉదాహరణ ఇవ్వండి.
జవాబు:
వస్తువు వేగం శూన్యమైనప్పటికీ దాని త్వరణం సున్న కానవసరం లేదు. ఉదా : నిట్టనిలువుగా పైకి విసిరిన వస్తువుకు గరిష్ఠ స్థానం వద్ద వేగము సున్న కానీ త్వరణం సున్న కాదు.

ప్రశ్న 4.
ఒక వాహనం ప్రయాణించిన దూరం L లో సగం దూరం వడి v₁ తోనూ, రెండవ సగం దూరం వడి v₂ ప్రయాణించింది. ఆ వాహనం సగటు వడి ఎంత?
జవాబు:
మొత్తం ప్రయాణానికి పట్టిన కాలము t = \(\frac{L}{2 v_1}+\frac{L}{2 v_2}=\frac{\left(v_2+v_1\right) L}{2 v_1 v_2}\)
∴ సగటు వేగము v = \(\frac{L}{t}=\frac{L}{\left(v_1+v_2\right) L} 2 v_1 v_2=\frac{2 v_1 v_2}{\left(v_1+v_2\right)}\)

ప్రశ్న 5.
కింది దిశలో ప్రయాణిస్తూ ఒక లిఫ్టుభూ అంతస్తు (ground floor) కు చేరబోతున్నది. భూ అంతస్తును మూల బిందువుగానూ, ఊర్ధ్వ దిశను ధన దిశగానూ అన్ని రాశులకూ ఎంపిక చేసుకొంటే కింద ఇచ్చినవాటిలో ఏది సరియైనది?
a) x < 0, v < 0, a > 0
c) x > 0, v < 0, a > 0
b) x > 0, v < 0, a < 0
d) x > 0, v > 0, a > 0
జవాబు:
దత్తాంశం నుండి భూ అంతస్తు మూలబిందువు ⇒ x = 0; ఊర్ధ్వ దిశ ధనాత్మకము అనగా అధోదిశకు v’ – ve’ ⇒ x < 0, v < 0 మరియు a < 0 లిఫ్ట్ భూమికి చేరబోతుంది. ఈ సందర్భంలో x < 0, v > 0 మరియు a < 0 అన్న నియమాలు వర్తిస్తాయి. కావున ఇచ్చిన వాటిలో (a) x < 0, v < 0, a > 0 అన్నది సరియైన సమాధానము.

ప్రశ్న 6.
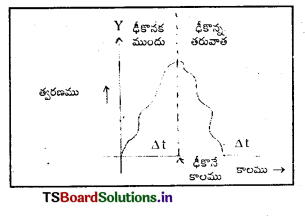
ఏకరీతి (సమరీతి) గమనం గల ఒక క్రికెట్ బంతి చాలా స్వల్పకాలం పాటు ఒక బ్యాట్తో కొట్టగా వెనుకకు మరలింది. తిరోదిశలో త్వరణాన్ని ధనాత్మకంగా తీసుకొని కాలంపరంగా త్వరణంలో మార్పుకు గ్రాఫు గీయండి.
జవాబు:
సమవేగంతో చలించే వస్తువుకు త్వరణము సున్న. బంతి, బ్యాటు కలిసి ఉన్న క్షణంలో బ్యాటు వలన బంతి గమనదిశకు వ్యతిరేకంగా కొంత త్వరణం ప్రయోగించబడింది. ఇది త్వరణం కాలం గ్రాఫ్ పటంలో చూపినట్లు ఉంటుంది.

ప్రశ్న 7.
ధన x − దిశలో అక్షం వెంబడి ఏకమితీయ గమనాన్ని కలిగి ఉండి, ఆవర్తకంగా నిశ్చలస్థితికి వచ్చి ముందుకు పోతూ ఉండే ఒక కణం గమనానికి ఉదాహరణ ఇవ్వండి.
జవాబు:
లోలకం పొడవు బాగా ఎక్కువగా ఉండి కంపన పరిమితి తక్కువగా ఉన్న సందర్భంలో లోలకం చలనం సరళరేఖ వెంబడి జరుగుతున్నట్లు భావించవచ్చు. గరిష్ఠ స్థానభ్రంశ బిందువు వద్ద లోలకం వేగం సున్న కాని దాని త్వరణం సున్న కాదు. ఈ రకమైన చలనం నిర్ణీత కాలవ్యవధి తరువాత పునరావృతమవుతుంది.

ప్రశ్న 8.
ఒక (ద్రవంలో) ప్రవాహిలో పతనం చెందే ఒక వస్తువు a = g – bv త్వరణం కలిగి ఉందని పరిశీలించడం జరిగింది. ఇక్కడ g గురుత్వ త్వరణం, b ఒక స్థిరాంకం. కొంతకాలం తరువాత వస్తువు స్థిర వేగంతో పతనం చెందుతుందని తెలుసుకొన్నారు. ఆ స్థిరవేగం విలువ ఎంతై ఉండవచ్చు?
జవాబు:
స్థిరవేగము అనగా త్వరణము a = 0. ఇచ్చిన సమీకరణం a = g – bv నుండి 0 = g – bv ⇒ v = \(\frac{\mathrm{g}}{\mathrm{b}}\) మీ/సె.

ప్రశ్న 9.
ఒక నిర్దేశ చట్రం పరంగా ఒక వస్తువు గమన పథం పరావలయం. ఈ నిర్దేశ చట్రం పరంగా స్థిర వేగంతో గమనంలో ఉన్న వేరొక నిర్దేశ చట్రం పరంగా వస్తువు గమన పథం పరావలయం అవుతుందా? కాకపోతే మరేమై ఉండవచ్చు?
జవాబు:
ఒక నిర్దేశ చట్రం పరంగా వస్తువు గమన పథం పరావలయము: ఈ నిర్దేశ చట్రం పరంగా రెండవ చట్రం స్థిరవేగంతో చలిస్తున్నది అంటే ఆ రెండు చట్రాలు జడత్వ నిర్దేశక చట్రాలే. కావున మొదటి చట్రంలో కనిపించిన పరావలయ గమన పథమే రెండవ దానిలో కూడా కనిపిస్తుంది.

ప్రశ్న 10.
ఒక స్ప్రింగు ఒక కొనను దృఢ ఆధారానికి బిగించి, రెండో కొనకు ఒక ద్రవ్యరాశిని వేలాడదీసి, లాగి వదిలారు. ఎప్పుడు త్వరణం పరిమాణం గరిష్ఠంగా ఉంటుంది?
జవాబు:
వ్రేలాడదీసిన స్ప్రింగ్ చివర బరువు తగిలించి లాగి వదిలితే అది సరళహరాత్మక చలనం చేస్తుంది. దత్తాంశం నుండి
F ∝ r. ఈ సందర్భంలో a = \(\frac{\mathrm{F}}{\mathrm{m}}=-\frac{\mathrm{K}}{\mathrm{m}} \mathrm{r}\) r. (r = స్థానభ్రంశము) గరిష్ఠ స్థానభ్రంశ బిందువుల వద్ద త్వరణము గరిష్ఠము.

స్వల్పసమాధాన ప్రశ్నలు

ప్రశ్న 1.
త్వరణం కాలంతోపాటు మారుతూ ఉన్నప్పుడు శుద్ధగతిశాస్త్రంలోని సమీకరణాలను ఉపయోగించవచ్చా? ఉపయోగించ వీలులేకపోతే ఆ సమీకరణాలు ఏ రూపాన్ని సంతరించుకొంటాయి?
జవాబు:
త్వరణం కాలంతోపాటు మారుతున్నది. అనగా వస్తువు అసమ త్వరణాన్ని కలిగి ఉంది. కావున గతి శాస్త్ర సమీకరణాలు ఇటువంటి సందర్భానికి వాడరాదు.

గతి శాస్త్ర సమీకరణాలు 1) v = v_o + at 2) x = v_ot + \(\frac{1}{2}\)at² 3) v² – v₀² = 2ax లలో ప్రతి సమీకరణంలోను త్వరణము ‘a’ ఉంది. ఇక్కడ ‘a’ సమత్వరణము కావున గతిశాస్త్ర సమీకరణాలను అసమత్వరణంతో చలించే వస్తువుకు వాడరాదు. అందువలన ఈ సమీకరణాలు ఏ రూపం సంతరించుకుంటాయి అన్న ప్రశ్న ఉండదు.

ప్రశ్న 2.
ఒక కణం ఒక సరళరేఖ వెంబడి సమత్వరణంతో గమనంలో ఉంది. t = 0 వద్ద కణం వేగం v_p, t = t వద్ద వేగం v₂, ఆ కణం సగటు వేగం, ఈ కాలవ్యవధిలో (v₁+v₂)/2 అని తెలిపితే, అది సరియైనదేనా? మీ సమాధానానికి తగిన వివరణ ఇవ్వండి.
జవాబు:
t = 0 వద్ద వేగము v₁ మరియు t = t వద్ద వేగము v₂ అయినపుడు సగటు వేగము v = \(\frac{v_1+v_2}{2}\) అన్న సమీకరణం సరియైనది.
వివరణ : దత్తాంశం నుండి కాలము t₁ = 0 మరియు t₂ = t. ల వద్ద వేగము v₁ మరియు v₂

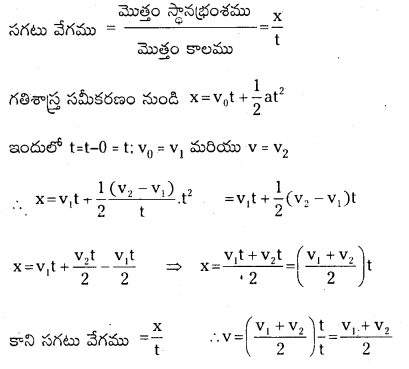
అనగా సగటు వేగము v = \(\frac{v_1+v_2}{2}\) సరియైనది అని నిరూపించబడినది.

ప్రశ్న 3.
ఒక కణం వేగ దిశ, కణ త్వరణ దిశతో పోల్చితే వేరుగా ఉండవచ్చా? అవును అయితే ఉదాహరణ ఇవ్వండి.
జవాబు:
వస్తువు వేగము మరియు త్వరణములు వేరు వేరు దిశలలో ఉండవచ్చును.

ఉదా :

1. ప్రక్షేపకాలలో క్షితిజ లంబదిశలో తొలి వేగము u_y = u sinθ. ఇది ఊర్ధ్వ దిశలో ఉంటుంది. కాని గురుత్వ త్వరణం అధోదిశలో ఉంటుంది. అనగా వేగము, త్వరణాలు వ్యతిరేక దిశలో ఉన్నాయి.
2. ప్రక్షేపకాలలో క్షితిజ సమాంతర దిశలో వేగము X అక్షము వెంబడి ఉంటుంది. కాని త్వరణము y- అక్షము వెంబడి ఉంటుంది. అనగా వేగము, త్వరణాలు పరస్పర లంబదిశలో ఉన్నాయి.

పై ఉదాహరణల నుండి వేగము, త్వరణాలు వేరువేరు దిశలలో ఉండవచ్చును అని తెలుస్తోంది.

ప్రశ్న 4.
ఎగురుతూ ఉన్న విమానం నుంచి పారాచూట్ సహాయంతో ఒక వ్యక్తి భూమి నుండి 3 km ఎత్తు నుంచి దూకాడు. అతడు భూమి నుంచి 1 km ఎత్తులో ఉన్నప్పుడు పారాచూట్ను పూర్తిగా విప్పాడు. అతడి గమనాన్ని వివరించండి.
జవాబు:
ఎ) పారాచూట్ తెరచుకోవడానికి ముందు కిందికి దిగిన దూరము h₁ = 2 km 2000 మీ.
∴ భూమి నుండి 1km ఎత్తు వద్ద వేగము v = \(\sqrt{2 \mathrm{gh}_1}=\sqrt{2 \times 10 \times 2000}\)
= \(\sqrt{40,000}\) = 200 మీ/సె.
2 km కిందికి దిగటానికి పట్టిన కాలము t = \(\sqrt{\frac{2 \mathrm{~h}_1}{\mathrm{~g}}}=\sqrt{\frac{2 \times 2000}{10}}\)
t = \(\sqrt{400}\) = 20 సె.

బి) పారాచూట్ తెరచుకున్న తరువాత అది భూమిని దాదాపు సున్న వేగంతో తాకుతుంది.

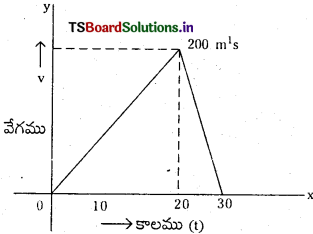
కావున తుది వేగము v = 0; తొలివేగము v_o = 200 మీ/సె,
తుదివేగము v_o = 0, x = h = 1000 మీ.
పారాచూట్ త్వరణము v² – v_o² = 2ax నుండి
a = \(\frac{0^2-200^2}{2 \times 1000}=\frac{-40000}{2000}\) = – 20 మీ/సె.
కాలము t = \(\frac{v_0}{a}=\frac{200}{-20}\) = 10 సె.
ఈ సందర్భములో v – t వక్రము ఆకృతి

ప్రశ్న 5.
ఒక పక్షి తన ముక్కున ఒక పండు కరుచుకుని భూమికి సమాంతరంగా ఎగురుతున్నది. ఒకానొక ఎత్తున అది పండును జారవిడిచింది. (ఎ) పక్షి పరంగానూ (బి) భూమిపై నిలబడిన వ్యక్తి పరంగానూ కింద పడుతున్న పండు గమన పథాన్ని వివరించండి.
జవాబు:
పక్షి భూమికి సమాంతరంగా ఎగురుతున్నది. కావున దాని నోటి నుండి జారిపడిన పండు తొలివేగం (V₀) క్షితిజ సమాంతరంగా ఉంటుంది. నోటి నుండి జారిన తరువాత పండు పై గురుత్వ త్వరణం ‘g’ పనిచేస్తుంది. కాని పక్షి మరియు పండు ఒకే క్షితిజ సమాంతర వేగం కలిగి ఉండడం వల్ల పక్షికి పండు నిట్టనిలువుగా క్రిందికి పడినట్లు కనిపిస్తుంది.

భూమిపై నిలబడి పరిశీలించిన వ్యక్తికి పండుకు గల క్షితిజ సమాంతర మరియు గురుత్వ త్వరణం వలన కలిగిన క్షితిజ లంబ అంశ వేగాల ఫలితమైన పరావలయ మార్గం కనిపిస్తుంది.

ప్రశ్న 6.
ఒకడు ఎత్తయిన భవన ఉపరితలంపై పరిగెడుతూ, పక్కనే కొద్దిగా తక్కువ ఎత్తున్న ఇంకొక భవనం పైకి క్షితిజ సమాంతరంగా దూకాడు. అతడి వేగం 9 m s^-1, రెండు భవనాల మధ్య దూరం 10 m, భవనాల ఎత్తులలో తేడా 9 m అయితే అతడు రెండవ భవనం పైకి దూకగలడా? (g = 10 m s^-2)
జవాబు:
తొలివేగము V₀ = 9 మీ/సె. భవనాల ఎత్తులలో తేడా = 9 మీ. భవనముల మధ్య క్షితిజ సమాంతర దూరము x = 10 మీ. ఆ వ్యక్తి సురక్షితంగా రెండవ భవనం మీదకు దూకడానికి అతని క్షితిజ సమాంతర వ్యాప్తి భవనముల మధ్య దూరము ‘x’ కన్నా ఎక్కువ ఉండాలి.
క్షితిజ సమాంతర వ్యాప్తి R = V₀ \(\sqrt{\frac{2 \mathrm{~h}}{\mathrm{~g}}}=9 \cdot \sqrt{\frac{2 \times 9}{10}}=9 \sqrt{1.8}\)
∴ R = 9 × 1.341 = 12.069
∵ R > x అతను సురక్షితంగా రెండవ భవనం మీదకు దూకుతాడు.

ప్రశ్న 7.
ఒక ఎత్తయిన భవనంపై నుంచి ఒక బంతిని జారవిడిచారు. అదే క్షణంలో అక్కడి నుంచే, ఇంకొక బంతిని కొంత వేగంతో క్షితిజ సమాంతరంగా విసిరారు. ఏ బంతి మొదటగా భూమిని చేరుతుంది? మీ సమాధానాన్ని వివరించండి.
జవాబు:
జారవిడిచిన బంతికి దిశలో తొలివేగం సున్న ⇒ V_ov = 0
క్షితిజ సమాంతరంగా విసరబడిన బంతికి ‘y’ దిశలో తొలివేగము సున్న ⇒ V_oy = 0
రెండు వస్తువులు కిందికి దిగిన దూరం ‘y’కు సమానము.
పైనుంచి వస్తువు కింద పడటానికి పట్టిన కాలము t = \(\sqrt{\frac{2 \mathrm{y}}{\mathrm{g}}}\)
రెండు వస్తువులకు స్త్రీ సమానము. ఎత్తు = సమానము కావున ఆ రెండు వస్తువులు ఒకేసారి క్రింద పడతాయి. గమనిక : వస్తువు కిందకు పడటానికి పట్టిన కాలము క్షితిజ సమాంతర దిశలో వేగంపై ఆధారపడదు.

ప్రశ్న 8.
ఒక భవనంపై నుంచి ఒక బంతిని జారవిడిచారు. అదే క్షణంలో ఇంకొక బంతిని నిట్టనిలువుగా పైకి కొంత వేగంతో విసిరారు. ఆ బంతుల సాపేక్ష వేగాలలో మార్పును కాలం ప్రమేయంగా వివరించండి.
జవాబు:
భవనంపై నుంచి జారవిడిచిన బంతికి తొలివేగము V_o = 0; ఏదైనా క్షణంలో దాని వేగము V₁ = V_o + gt = gt ……………….. (1)
నిట్టనిలువుగా పైకి విసిరిన బంతికి తొలివేగము V_o = u అనుకోండి.
వస్తువుకు ఏదైనా క్షణంలో వేగము V₂ = V_o – gt = u – gt ……………….. (2)
ఈ వస్తువులు వ్యతిరేక దిశలో చలించడం వల్ల వాటి సాపేక్ష వేగము V_R = V₂ + V₁ = u – gt + gt = u.
ఈ సందర్భంలో వాటి మధ్య సాపేక్ష వేగము ‘u’. ఇది కాలంతో పాటు మారదు. ఎందుకనగా మొదటి వస్తువు వేగం ఎంత పెరిగితే పైకి విసిరిన వస్తువు వేగం అదే కాలంలో అంతే తగ్గుతుంది కావున.

ప్రశ్న 9.
ఒకానొక వర్ష బిందువు వ్యాసం 4 mm. భూమి నుంచి 1 km ఎత్తున గల మేఘం నుంచి ఆ వర్ష బిందువు జారిపడితే అది భూమిని ఎంత ద్రవ్యవేగంతో తాకుతుంది?
జవాబు:
వర్షపు బిందువు వ్యాసము D = 4 మి.మీ. ⇒ వ్యాసార్ధము r = 2 మి.మీ. = 2 × 10^-3m.
వర్షపు బిందు ద్రవ్యరాశి m = ఘ.ప. x సాంద్రత = \(\frac{4}{3}\) πг³ × 1000
(∵ నీటి సాంద్రత d = 1000 kg/m³ కావున)
∴ m = \(\frac{4}{3}\) × \(\frac{22}{7}\) × (2 × 10^-3)³ ×1000 = \(\frac{4}{3}\) × \(\frac{22}{7}\) × 8 × 10^-9 × 10³
= 33.52 × 10^-6 Kg
ఎత్తు h = 1 కి.మీ. 1000 మీ.; g = 9.8 మీ/సె²
నేలను తాకుటకు ముందు వేగము V = \(\sqrt{2 \mathrm{gh}}=\sqrt{2 \times 9.8 \times 1000}\)
= \(\sqrt{19600}\) = 140 మీ/సె.
∴ నీటి బిందువు ద్రవ్యరాశి వేగము \(\overline{\mathrm{p}}\) = m V = 33.52 × 10^-6 × 140
= 4.693 × 10^-3 Kg-m

ప్రశ్న 10.
క్షితిజంతో 45° కోణంతో ప్రక్షిప్తం చేసిన ప్రక్షేపకం చేరే గరిష్ఠ ఎత్తు దాని వ్యాప్తిలో నాలుగో వంతు ఉంటుందని చూపండి.
జవాబు:
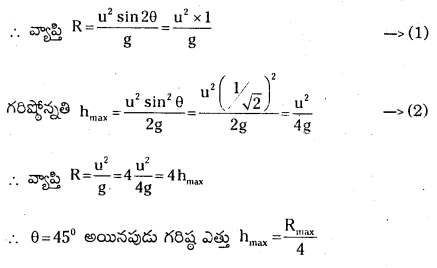
ప్రక్షేపకాలలో వ్యాప్తి R = \(\frac{u^2 \sin 2 \theta}{\mathrm{g}}\)
గరిష్లోన్నతి h_max = \(\frac{\mathrm{u}^2 \sin ^2 \theta}{2 \mathrm{~g}}\)
ప్రక్షేపకోణము θ = 45°;
sin45 = \(\frac{1}{\sqrt{2}}\)

అదనపు ప్రశ్నలు

ప్రశ్న 1.
వేగ – కాల వక్రాలు అనగానేమి? వివిధ రకాలైన వేగ – కాల వక్రాల ఆకృతులు, వాటి ఉపయోగాలు తెలుపండి.
జవాబు:
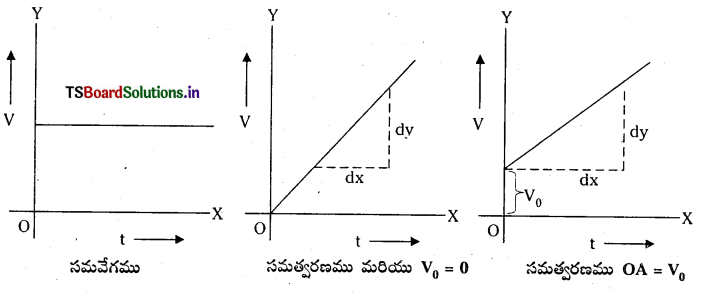
వేగ – కాల వక్రాలు (V-t గ్రాఫ్) : వేగము Vని Y- అక్షం మీద, కాలము t ని X- అక్షం మీద తీసుకొని గీచిన రేఖా పటాన్ని వేగ ‘కాల వక్రము అంటారు. వేగ కాలవక్రాలలో
a) సమవేగంతో చలించే వస్తువు వేగ – కాల వక్రం X- అక్షానికి సమాంతరంగా గల సరళరేఖ.
b) నిశ్చలస్థితి నుండి బయలుదేరి సమత్వరణంతో చలించే వస్తువు వేగ – కాల వక్రం మూల బిందువు గుండా పోవు సరళరేఖ.
c) తొలివేగం ‘V₀‘ తో బయలుదేరి సమత్వరణంతో చలించు వస్తువు వేగ – కాల వక్రం కొంత Y అంతరఖండం కలిగి X- అక్షంతో కొంత కోణం చేయు సరళరేఖ. దీని Y అంతర ఖండం తొలివేగం ‘V₀‘ ను ఇస్తుంది.
d) వేగ – కాల వక్రం వాలు వస్తువు సమత్వరణం ‘a’ ను ఇస్తుంది.
e) వేగ – కాల వక్రం కింద గల వైశాల్యం వస్తువు మొత్తం స్థానభ్రంశం ‘s’ ను తెలియజేస్తుంది.
f) వేగ – కాల వక్రాల నుండి గతి శాస్త్ర సమీకరణములు V = V₀ + at, X = V₀t + \(\frac{1}{2}\)at², V² – V₀² = 2ax లను ఉత్పాదించవచ్చు.

ప్రశ్న 2.
వేగ – కాల వక్రాల నుండి గతిశాస్త్ర ప్రాథమిక సమీకరణాలు ఉత్పాదించండి.
జవాబు:
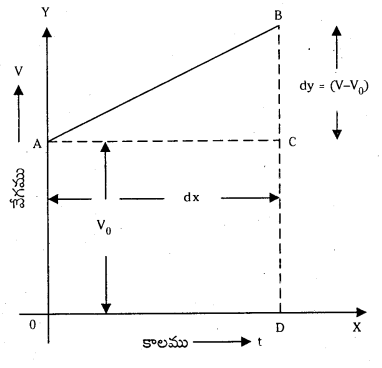
తొలివేగము ‘V₀‘ తో బయలుదేరి సమత్వరణము ‘a’ తో చలించు వస్తువు వేగ – కాల వక్రము పటంలో చూపినట్లు ఉంటుంది.
1) V = V₀ + at ఉత్పాదన :
వేగకాల వక్రం వాలు \(\frac{\mathrm{dy}}{\mathrm{dx}}\) వస్తువు త్వరణము

‘a’ ను సూచిస్తుంది.
పటంలో AC = dx = t
BC = DB – DC = V – V₀ = dy
∴ త్వరణము \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = a = \(\frac{V-V_0}{t}\)
⇒ at = V – V₀ లేదా V = V₀ + at

2) X = V₀t + \(\frac{1}{2}\) at² ఉత్పాదన :
వేగ – కాల వక్రాల కింద గల వైశాల్యము మొత్తం స్థానభ్రంశాన్ని సూచిస్తుంది.
∴ మొత్తం స్థానభ్రంశము x = OABD వైశాల్యము = దీర్ఘచతురస్రము
OACD వైశాల్యము + త్రిభుజము ABC వైశాల్యము ……………. (1)
OACD వైశాల్యము = OA × OD = V_o × t …………….. (2)
త్రిభుజము ABC వైశాల్యము = \(\frac{1}{2}\) × AC × CD = \(\frac{1}{2}\)t(V – V₀)
కాని V – V₀ = at
∴ త్రిభుజ వైశాల్యము = \(\frac{1}{2}\)t at = \(\frac{1}{2}\)at² …………….. (3)
1, 2, 3 సమీకరణాల నుండి x = V₀t + \(\frac{1}{2}\) at²

3) V² – V₀² = 2ax ఉత్పాదన :
వస్తువు మొత్తం స్థానభ్రంశము X = సగటువేగము × కాలము
సగటు వేగము = \(\frac{V+V_0}{2}\) మరియు కాలము t = \(\frac{V-V_0}{2}\)
∴ x = \(\left(\frac{\mathrm{V}+\mathrm{V}_0}{2}\right)\left(\frac{\mathrm{V}-\mathrm{V}_0}{\mathrm{a}}\right)=\frac{\mathrm{V}^2-\mathrm{V}_0^2}{2 \mathrm{a}}\) లేదా V² – V₀² = 2ax

లెక్కలు

ప్రశ్న 1.
ఒకడు ఒక తిన్నని రోడ్డు వెంట తన ఇంటి నుంచి 2.5 km దూరాన ఉన్న మార్కెట్కు 5 km h^-1 వడితో నడిచాడు. మార్కెట్ మూసి ఉండటం గమనించి, వెంటనే వెనుదిరిగి ఇంటికి 7.5 km ho వేగంతో చేరాడు. 0 నుండి 50 నిమిషాల కాలవ్యవధిలో అతడి (a) సగటు వేగ పరిమాణం, (b) సగటు వడి ఎంత?
సాధన:

ప్రశ్న 2.
ఒక కారు మొదటి మూడు వంతుల దూరాన్ని 10 kmph వేగంతోనూ, రెండవ మూడువంతుల దూరాన్ని 20 kmph వేగంతోనూ, చివరి మూడు వంతుల దూరాన్ని 60 kmph వేగంతోనూ ప్రయాణిస్తే, మొత్తం దూరాన్ని పూర్తి చేయడంలో కారు సగటు వడి ఎంత? (మే 2014)
సాధన:
మొత్తము దూరము = s;
ప్రయాణించిన దూరము, s₁ = \(\frac{s}{3}\) ; వేగము, v₁ = 10 kmph
దూరము, s₂ = \(\frac{s}{3}\) వేగము, v₂ = 20 kmph
దూరము, s₃ = \(\frac{s}{3}\) వేగము, v₃ = 60 kmph

ప్రశ్న 3.
ఒక తుపాకి గుండు 150 m s^-1 వడితో ప్రయాణిస్తూ చెట్టును తాకి 3.5 cm దూరం దూసుకొని పోయి ఆగిపోయింది. చెట్టు కాండంలో గుండు ఋణత్వరణం పరిమాణం, చెట్టును తాకిన తరువాత గుండు ఆగిపోవడానికి పట్టిన కాలం ఎంత?
సాధన:
బుల్లెట్ తొలి వేగము, u = 150 m/s; తుది వేగము, v = 0
ప్రయాణించిన దూరము, s = 3.5 cm = 3.5 × 10^-2 m,
a) త్వరణము, a = \(\frac{\mathrm{v}^2-\mathrm{u}^2}{2 \mathrm{~s}}=\frac{0^2-150^2}{2 \times 3.50 \times 10^{-2}}=\frac{22500}{7 \times 10^{-2}}\) = 3.214 × 10⁵ m / sec²
(−గుర్తు ఋణత్వరణము)
b) ఆగిపోవుటకు పట్టిన కాలము, t = \(\frac{\mathrm{v}-\mathrm{u}}{\mathrm{a}}=\frac{-150}{-3.214 \times 10^5}\) = 4.67 × 10^-4 sec.

ప్రశ్న 4.
ఒక మోటారు వాహకుడు మోటారును 30 నిమిషాలపాటు 85 km/h వేగంతో ఉత్తర దిశగా నడిపి 15 నిమిషాలపాటు ఆగిపోయాడు. తరువాత ఉత్తర దిశలోనే ప్రయాణించి 2 గంటలలో 130 km దూరం వెళ్ళాడు. అతడి మొత్తం స్థానభ్రంశం, సగటు వేగం ఎంత?
సాధన:
మొదటి భాగములో :
వేగము, v₁ = 85 kmph
కాలము, t₁ = 30 ని.
ప్రయాణించిన దూరము
s₁ = v₁ t₁ = 85 × \(\frac{30}{60}\) = 42.5 km
రెండవ భాగములో :
ప్రయాణించిన దూరము, s₂ = 0
కాలము, t₂ = 15.0 ని.
మూడవ భాగములో :
ప్రయాణించిన దూరము, s₃ = 130 km కాలము, t₃ = 120 ని. = 2 గం.
a) ప్రయాణించిన మొత్తం దూరము, s = s₁ + s₂ + s₃ = 42.5 + 0 + 130 = 172.5 km
b) ప్రయాణించిన మొత్తం కాలము, t = t₁ + t₂ + t₃ = 30 + 15 + 120 = 165 ని. = 2 గం. 45 నిమిషాలు

= 2 \(\frac{3}{4}\) గంటలు = \(\frac{11}{4}\) గంటలు
∴ సగటు వేగము, v_avg = \(\frac{172.5}{\frac{11}{4}}\) = 62.7 kmph.

ప్రశ్న 5.
ఒక భవనం పైకప్పు నుంచి బంతి Aని జారవిడిచిన క్షణంలోనే, అలాంటిదే బంతి B ను భూమిపై నుంచి నిట్టనిలువుగా పైకి విసిరారు. బంతులు ఢీకొట్టుకున్న క్షణంలో బంతి A వడి, బంతి B వడికి రెట్టింపు ఉంది. బంతులు అభిఘాతం జరుపుకొన్న ఎత్తు, భవనం ఎత్తులో ఎన్నో వంతు ఉంటుంది?
సాధన:
దత్తాంశం నుండి వస్తువులు ఢీ కొనేటప్పుడు A వస్తువు వేగము V_A = 2 × V_B (B వేగము)
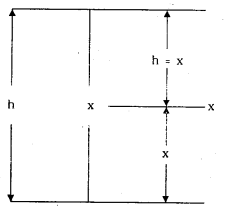
‘A’ ను h ఎత్తు నుంచి జారవిడిచినారనుకొనుము. రెండు వస్తువులు భూమి నుండి x ఎత్తులో ఢీకొన్నవి అనుకొనుము.
జారవిడిచిన వస్తువుకు S_A = h – x = \(\frac{1}{2}\) gt² ………….. (1)
పైకి విసిరిన వస్తువుకు S_B = x = ut – \(\frac{1}{2}\) gt² ………….. (2)
x వద్ద జారవిడిచిన వస్తువు వేగము V_A = 0 + gt = gt …………….. (3)
పైకి విసిరిన వస్తువుకు x వద్ద వేగము V_B = u – gt ………………. (4)
కాని V_A = 2 × V_B ⇒ gt = 2 (u – gt) లేదా u = \(\frac{3 \mathrm{gt}}{2}\) …………… (5)


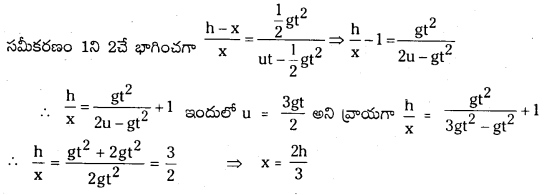
అనగా మొత్తం ఎత్తులో వస్తువులు ఢీకొన్న సమయంలోని ఎత్తు భాగము = \(\frac{2}{3}\)

ప్రశ్న 6.
16 m ఎత్తు గల ఒక భవనం పై కప్పు నుంచి క్రమ కాలవ్యవధులలో నీటి బిందువులు పడుతున్నాయి. మొదటి నీటి బిందువు భూమిని తాకిన క్షణంలో, అయిదవ నీటి బిందువు పైకప్పును వదిలింది. వరుస నీటి బిందువుల మధ్య దూరం కనుక్కోండి.
సాధన:
భూమి నుండి ఇంటి పైకప్పు ఎత్తు, h = 16 m
నీటి బిందువు భూమిని చేరుటకు పట్టు కాలము, t = \(\sqrt{\frac{2 h}{g}}\)
∴ t = \(\sqrt{\frac{2 \times 16}{9.8}}=\sqrt{\frac{32}{9.8}}=\sqrt{3.26}\)= 1.8 సెం.
మొత్తం బిందువుల సంఖ్య, n = 5
కాల వ్యవధుల సంఖ్య = n – 1 = 5 – 1 = 4
ఒక్కొక్క బిందువు మధ్య కాలవ్యవధి = \(\frac{1.8}{4}\) = 0.45 సె.
మొదటి బిందువు ప్రయాణించిన కాలము t₁ = 4 × 0.45 = 1.8 సె.
∴ ప్రయాణించిన దూరము
S₁ = \(\frac{1}{2}\)gt₁² = \(\frac{1}{2}\) × 9.8 × 1.8 ×1.8 = 16 m
రెండవ నీటి బిందువు విషయంలో t₂ = 3 × 3t₁ = 3 × 0.45 = 1.35 sec.
ప్రయాణించిన దూరము S₂ = \(\frac{1}{2}\)gt₂²
∴ S₂ = \(\frac{1}{2}\) × 9.8 × 1.35² = 4.9 × 1.822 = 9m
మూడవ బిందువు విషయంలో, t₃ = 2 × 0.45 = 0.9 sec.
ప్రయాణించిన దూరము, S₃ = \(\frac{1}{2}\)gt₃² = \(\frac{1}{2}\) × 9.8 × 0.9² = 3.97 ≃ 4m
నాల్గవ బిందువు విషయంలో. t₄ = 1 × 0.45 = 0.45 sec
ప్రయాణించిన దూరము S₄ = \(\frac{1}{2}\)gt₄² = \(\frac{1}{2}\) × 9.8 × (0.45)² ≃ 1 m
ఐదవ బిందువు విషయంలో t₅ = 0 × 0.45 = 0 sec.
దూరము S₅ = \(\frac{1}{2}\)gt₅² = 0 m

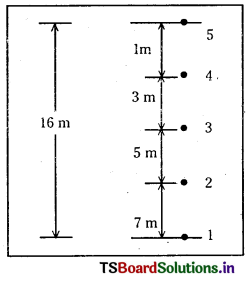
1వ మరియు 2వ బిందువుల మధ్య దూరము S₁¹ = S₁ – S₂ = 16 – 9 = 7 m
2వ మరియు 3వ బిందువుల మధ్య దూరము S₂¹ = S₂ – S₃ = 9 – 4 = 5 m
3వ మరియు 4వ బిందువుల మధ్య దూరము S₃¹ = S₃ – S₄ = 4 – 1 = 3 m
4వ మరియు 5వ బిందువుల మధ్య దూరము S₄¹ = S₄ – S₅ = 1 – 0 = 1 m
∴ వరుస బిందువుల మధ్య దూరములు 7m, 5m, 3m మరియు 1m.

ప్రశ్న 7.
ఒక వేటగాడు తనకు కొంత దూరంలో ఉన్న చెట్టు నుంచి వేలాడుతున్న ఒక కోతికి తుపాకీ గురిపెట్టాడు. వేటగాడు తుపాకీ పేల్చిన క్షణాన, గుండు తగలకుండా తప్పించుకోవాలని కోతి కొమ్మను విడిచి జారిపడింది. కోతిది తప్పుడు నిర్ణయం అని వివరించండి.
సాధన:
బుల్లెట్ను ప్రక్షిప్తం చేసిన కోణం α అనుకొనుము.
వేటగాని నుండి కోతికి గల దూరము = x అనుకొనుము.
కోతిని ఖచ్చితంగా గురిపెట్టినపుడు s_y = v sinα t = h
గురుత్వ త్వరణం వలన h₁ = u sin α t – \(\frac{1}{2}\) gt² = h – \(\frac{1}{2}\) gt² ………………… (1)
కనుక కోతి క్రింద నుండి బుల్లెట్ పోయిన దూరము = \(\frac{1}{2}\) gt²
అయితే కోతి స్వేచ్ఛగా క్రిందకు పడుతున్నప్పుడు t సెకనులలో ప్రయాణించిన దూరము t = \(\frac{1}{2}\) gt²
అయిన కొత్త దూరము h₂ = h – \(\frac{1}{2}\) gt² …………. (2)
∴ సమీకరణము (1) మరియు (2)ల నుండి h₁ = h₂ ఋజువైనది. కనుక కోతి చేతులు వదిలివేసి జారటం వల్ల బుల్లెట్ ఖచ్చితంగా దానికి తాకింది. అనగా ఆ కోతి పొరపాటు పడింది.

ప్రశ్న 8.
భూమి నుంచి 500 m ఎత్తున 360 kmph వడితో క్షితిజ సమాంతర దిశలో ప్రయాణిస్తున్న విమానం నుంచి ఆహారపు పొట్లాన్ని జారవిడిచారు. (i) పొట్లం అవరోహణ కాలం, (ii) జారవిడిచిన బిందువు నుండి క్షితిజ సమాంతరంగా ఎంత దూరంలో పొట్లం భూమిని చేరుతుందో కనుక్కోండి.
సాధన:
విమానం వేగము V = 360 kmph = 360 × \(\frac{5}{18}\) = 100 మీ/సె.
భూమి నుండి ఎత్తు h = 500 మీ; g = 10 మీ/సె²
i) భూమిని చేరటానికి పట్టిన కాలం = పలాయన కాలం t = \(\sqrt{\frac{2 h}{g}}=\sqrt{\frac{2 \times 500}{10}}=\sqrt{100}\) = 10 సెకనులు
ii) జారవిడిచిన బిందువు నుండి భూమి లంబ పాదాన్ని తాకే దూరం = వ్యాప్తి (R).
∴ వ్యాప్తి (R) = u \(\sqrt{\frac{2 \mathrm{~h}}{\mathrm{~g}}}=100 \sqrt{\frac{2 \times 500}{10}}=100 \sqrt{100}\) = 1000 మీ.

ప్రశ్న 9.
ఒక భవనం కిటికీ నుంచి, క్షితిజానికి 20° కిందగా, 8 ms^-1 వేగంతో ఒక బంతిని విసిరారు. బంతి భూమిని 3s తరువాత తాకింది. బంతిని ఎంత ఎత్తు నుంచి విసిరారు? భవనం పునాది నుంచి ఎంత దూరంలో బంతి భూమిని తాకుతుంది?
సాధన:
తొలివేగము u = 8 మీ/సె;
ప్రక్షిప్త కోణము θ = 20° ;
భూమిని చేరుటకు పట్టు కాలము t = 3 సె.
క్షితిజ సమాంతర తొలివేగము u_x = u. cos θ = 8 cos 20° = 8 × 0.94 = 7.52 మీ/సె
నిలువుతులం దిశలో తొలివేగము v_y = u sin θ = 8 sin 20° = 8 × 0.342 = 2.786 మీ/సె
a) t సెకనులలో క్షితిజ సమాంతరంగా ప్రయాణించిన దూరము X = u_xt = 7.52 × 3 = 22.56 మీ

b) బంతిని విసిరిన ఎత్తు h = -u_yt + \(\frac{1}{2}\)gt²
h = -2.786 × 3 + \(\frac{1}{2}\) × 9.8 × 3² = -8.208 + 44.1 = 35.9 మీ.

c) 10 మీ క్రింద ఉన్న బిందువును చేరటానికి పట్టిన కాలము లెక్కించుట
h₁ = 10m
u_y = 2.786 = 2.8 m/s, t₁ = ?
h₁ = -u_yt₁ + \(\frac{1}{2}\)gt₁² ⇒ 10 = -2.8 × t₁ + \(\frac{1}{2}\) × 10 × t₁²
∴ 10 = -2.8t₁ + 5t₁² ⇒ 2.8 t – 10 = 0
t = \(\frac{2.8 \pm \sqrt{2.8^2-(4 \times 5 \times(-10))}}{2 \times 5}=\frac{2.8 \pm 14.42}{10}\)
⇒ t = 1.722 సె.

ప్రశ్న 10.
క్షితిజంతో 30°, 60° చేసే దిశలలో, ఒకే బిందువు నుంచి రెండు బంతులను ప్రక్షిప్తం చేశారు. ఆ రెండు బంతులూ (a) ఒకే ఎత్తును చేరితే, (b) ఒకే వ్యాప్తిని కలిగి ఉంటే వాటి తొలివేగాల నిష్పత్తి ఎంత?
సాధన:
మొదటి బంతి ప్రక్షేప కోణము θ₁ = 30°
రెండవ బంతి ప్రక్షేప కోణము θ₂ = 60°
బ వేగాలు u₁ మరియు u₂ అనుకుందాం.
(a) దత్తాంశం నుండి అవి ఒకే గరిష్ఠ ఎత్తును చేరాయి అనగా h_{max 1} = h_{max 2}

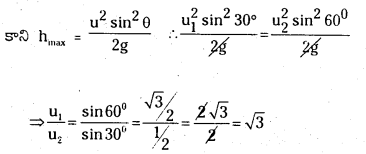
∴ వాటి తొలివేగాల నిష్పత్తి 3:1

(b) దత్తాంశం నుండి వాటి వ్యాప్తి సమానము.
వ్యాప్తి R = \(\frac{u^2 \sin 2 \theta}{g} \Rightarrow \frac{u_1^2 \sin 60^{\circ}}{g}=\frac{u_2^2 \sin 120^{\circ}}{g}\)
⇒ \(\frac{u_1^2}{u^2}=\frac{\sin 120^{\circ}}{\sin 60^{\circ}}=\frac{\cos 30^{\circ}}{\sin 60^{\circ}}=\frac{\sqrt{3} / 2}{\sqrt{3} / 2}\) = 1 (∵ sin 120° = cos 30°)
∴ వేగాల నిష్పత్తి u₁ : u₂ = 1 : 1

ముఖ్యమైన ఉదాహరణ లెక్కలు

ప్రశ్న 1.
ఒక కారు ఒక సరళరేఖ వెంబడి, OP అనుకుందాం, గమనంలో ఉన్నది. అది 18sలో 0 నుంచి P బిందువును చేరి మరల P నుంచి బిందువు ను 6.08 లలో చేరింది. (a) O నుంచి P ను చేరినప్పుడు, (b) O నుంచి P ను, అటు నుంచి వెనుదిరిగి Q ను చేరినప్పుడు వస్తువు సగటు వేగం, సగటు వడి విలువలేమిటి?
సాధన:

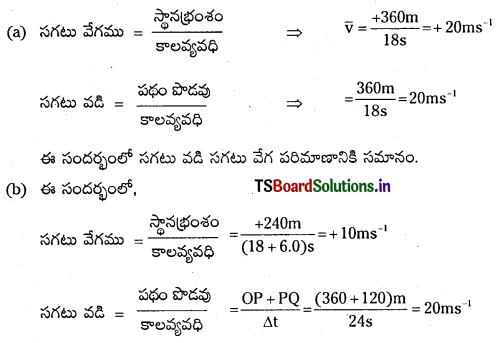
ప్రశ్న 2.
x- అక్షం వెంబడి గమనంలో ఉన్న ఒక వస్తువు స్థానం x = a + bt² గా ఇవ్వడమైంది. ఇక్కడ a = 8.5m, b = 2.5ms^-2, t ను సెకండ్లలో కొలిచారు. t = 0s,t = 2.0 s వద్ద వేగం ఎంత? t = 2.0 s, t = 4.0 s మధ్య సగటు వేగం ఎంత?
సాధన:
వేగము v = \(\frac{d x}{d t}=\frac{d}{d t}\) (a + bt²) = 2bt = 5.0tms^-1
t = 0 s వద్ద v = 0 ms^-1, t = 2.0s వద్ద v=10 ms^-1
సగటు వేగం \(\frac{x_2-x_1}{t_2-t_1}=\frac{x(4.0)-x(2.0)}{4.0-2.0}\)
= \(\frac{a+16 b-a-4 b}{2.0}\) = 6.0 × b = 6.0 × 2.5 = 15 ms^-1

ప్రశ్న 3.
ఉత్తర – దక్షిణ దిశలో రెండు సమాంతర రైలు మార్గాలున్నాయి. రైలు A 54 km h^-1 వడితో ఉత్తరం వైపు, రైలు B 90 km h^-1 వడితో దక్షిణంవైపు ప్రయాణిస్తున్నాయి. (a) A పరంగా B వేగం ఎంత? (b) B పరంగా భూమి వేగం ఎంత? (c) రైలు A పైకప్పుపై 18km h^-1 వేగంతో రైలు వేగానికి వ్యతిరేక దిశలో పరుగెడుతున్న కోతి సాపేక్ష వేగం భూమిపై నిల్చున్న పరిశీలకుడి పరంగా ఎంత?
సాధన:
దక్షిణం నుండి ఉత్తరంవైపు ధన x – అక్షం దిశగా ఎంచుకొందాం. అప్పుడు,
V_A = +54 kmh^-1 = 15 ms^-1
V_B = -90 kmh^-1 = -25ms^-1
A పరంగా B సాపేక్ష వేగం = v_B – v_A = -40ms^-1, అంటే రైలు A పరంగా రైలు B 40m s^-1 వడితో ఉత్తరం నుంచి దక్షిణంవైపు ప్రయాణిస్తున్నట్లు అనిపిస్తుంది.
రైలు B పరంగా భూమి సాపేక్ష వేగం = 0 – v_B = 25 ms^-1
భాగం (c) లో భూమి పరంగా కోతి వేగం v_M అనుకొందాం. రైలు A పరంగా కోతి సాపేక్ష వేగం
V_MA = V_M – V_A = -18 kmh^-1 = -5ms^-1. అందువల్ల V_M = (15 – 5)ms^-1 =10m s^-1

ప్రశ్న 4.
ఒక బహుళ అంతస్థు పైభాగం నుంచి ఒక బంతిని నిట్టనిలువుగా పైకి 20 m s^-1 వేగంతో విసిరారు. బంతిని విసిరిన బిందువు భూమి నుంచి 25.0m ఎత్తున ఉంది. (a) బంతి ఎంత ఎత్తుకు ఎగురుతుంది? (b) విసిరిన తరువాత బంతి భూమిని తాకడానికి ఎంత కాలము పడుతుంది? g = 10 ms^-2 గా తీసుకోండి (g నిజ విలువ 9.8 ms^-2).
సాధన:
తొలివేగము v_o = 20 m / s; గురుత్వత్వరణము g = 10m/s²
భవనం ఎత్తు = y_o = 25 మీ; తుదివేగము v = 0
(a) బంతి చేరిన ఎత్తు భవనం నుండి = y – y_o
v² – v_o² = 2a(y – y_o) నుండి 0 – 20² = 2 × 10(y – y_o)
y – y_o = \(\frac{0-20^2}{20}\) = 20 మీ.

(b)బంతి నేలను తాకటానికి పట్టిన కాలము t = ?
ఈ సందర్భానికి y = y_o + v_ot + \(\frac{1}{2}\)at² ను వాడవలెను.
ఇందులో y_o = 25మీ, v_o = 20 మీ/సె. g = -10మీ/సె²
మొత్తం స్థానభ్రంశము y = 0 (భూమి నుండి)
∴ 0 = 25 + 20t – \(\frac{1}{2}\) 10t² ⇒ -5t² + 20t + 25 = 0
లేదా t² – 4t – 5t² = 0 దీనిని సాధించగా
(t – 5)(t + 1) = 0 అనగా t = 5 సె లేదా t = -1 సె కాలము ‘ఋణాత్మకం’ కాదు కావున రాయి భూమిని చేరుటకు పట్టినకాలము t = 5 సె.

అదనపు లెక్కలు.

ప్రశ్న 1.
కింద ఇచ్చిన గమన సంబంధ ఉదాహరణలలో దేనిలో వస్తువును బిందు వస్తువుగా ఉజ్జాయింపు చేయవచ్చు.
a) రెండు స్టేషన్ల మధ్య కుదుపులు లేకుండా ప్రయాణించే రైలు కారేజ్.
b) వృత్తాకార మార్గంలో సైకిల్ తొక్కే వ్యక్తి తలపై కూర్చున్న కోతి.
c) స్పిన్ తిరుగుతూ భూమిని తాకి హఠాత్తుగా మలుపు తిరిగిన క్రికెట్ బంతి.
d) టేబుల్ అంచు నుంచి జారిపడి అటూ ఇటూ దొర్లుతున్న బీకర్.
సాధన:
a) స్టేషన్ల మధ్య దూరంతో పోలిస్తే రైలు క్యారేజ్ పరిమాణం చాలా చిన్నది. కావున దీన్ని బిందు పరిమాణ వస్తువుగా భావించవచ్చు.

b) వృత్తాకార మార్గ వ్యాసార్ధం బాగా ఎక్కువగా ఉంటే కోతిని బిందు పరిమాణ వస్తువుగా భావించవచ్చు.

c) బంతి, భూమిని తాకి ఉన్న పరిమాణంతో పోలిస్తే బంతి పరిమాణం పెద్దది కావున దీనిని బిందు పరిమాణ వస్తువుగా భావించలేము.

d) బల్ల ఎత్తుతో పోల్చితే బీకరు పరిమాణాన్ని విస్మరించలేము కావున దీనిని బిందు పరిమాణ వస్తువుగా భావించలేము.

ప్రశ్న 2.
ఇద్దరు పిల్లలు A, B లు వారి స్కూలు () నుంచి వారి ఇళ్ళు P,Q లకు తిరిగి ప్రయాణమయ్యే సందర్భంలో వారి గమనాన్ని సూచించే స్థానం – కాలం (x – t) గ్రాఫు చూపడం జరిగింది. కింద ఇచ్చిన బ్రాకెట్లలో సరియైన
ఎంపికచేయండి.
a) (A/B) స్కూలుకు (B/A) కంటే దగ్గరగా ఉంటాడు.
b) (A/B) స్కూలుకు (B/A) కంటే ముందుగా బయలుదేరుతాడు.
c) (A/B), (B/A) కంటే వేగంగా నడుస్తాడు.
d) A, B లు ఇంటికి (ఒకే సమయంలో / వేరు వేరు సమయాలలో) చేరుతారు.
e) (A/B) ప్రయాణంలో (B/A) ను (ఒకసారి/రెండుసార్లు) దాటి వెళతాడు.

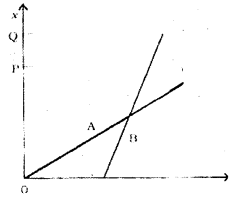
సాధన:
a) P బిందువు Q కన్నా దగ్గరగా ఉంది. OP < OQ కావున A ఇల్లు B ఇంటి కన్నా దగ్గర.

b) A విషయంలో t = 0 వద్ద x = 0. కాని B విషయంలో t = 0 వద్ద x ≠ 0 కావున B కన్న A ముందుగా స్కూల్ నుండి బయలుదేరతాడు.

c) x – t గ్రాఫ్ వాలు సమవేగాన్ని ఇస్తుంది. పటంలో A ప్రయాణించిన వక్రం వాలుకన్నా B స్థానభ్రంశ రేఖ వాలు ఎక్కువ. అనగా B ఎక్కువ వేగంతో ప్రయాణిస్తాడు.

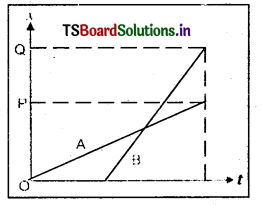
d) పటంలో P, Q రేఖల నుండి x- అక్షానికి సమాంతర రేఖలు గీస్తే అవి A, B లకు చెందిన రేఖాపటాలను ఒకే కాల వ్యవధి వద్ద ఖండిస్తాయి. అనగా A, B లు ఇద్దరు ఒకేసారి ఇంటికి చేరతారు.

e) ఇచ్చిన రేఖాపటం నుండి A, B రేఖలు ఒకేసారి ఖండించుకున్నాయి. అనగా వారు మార్గంలో ఒకసారి మాత్రమే కలుసుకుంటారు.

ప్రశ్న 3.
ఒక స్త్రీ ఇంటి వద్ద 9 am కు బయలుదేరి, కాలి నడకన 5km h^-1 వడితో తిన్నని రోడ్డుపై 2.5 km దూరంలో ఉ న్న కార్యాలయానికి చేరి, 5pm వరకు అక్కడ ఉండిపోయి, ఆటోలో 25 km h^-1 వడితో తిరిగి ఇంటికి చేరింది. తగిన స్కేలు తీసుకొని ఆ స్త్రీ గమనానికి సంబంధించి x – t గ్రాఫు గీయండి.
సాధన:

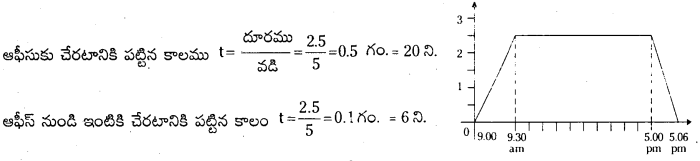
ఆమె 9.00 గం.ల నుండి 9.30 గం.ల వరకు చలనంలోను, 9.30 గం.ల నుండి సాయంత్రం 5 గం.ల వరకు స్థిరంగాను, మరలా 5.00 గం.ల నుండి 5 గం. 6 నిమిషాల వరకు చలనంలోను ఉంది. ఆమె స్థానభ్రంశ కాలవక్రము పై గ్రాఫులో చూపిన విధంగా ఉంటుంది.

ప్రశ్న 4.
ఒక వ్యక్తి సన్నని వీధిలో 5 అడుగులు ముందుకు, 3 అడుగులు వెనక్కి మరల 5 అడుగులు ముందుకు, 3 అడుగులు వెనక్కి ఇలా నడిచాడు. ప్రతి అడుగులో అతడు 1 m దూరం, 1 సెకనులో ప్రయాణిస్తే, అతని గమనానికి x-t గ్రాఫు గీయండి. వ్యక్తి తాగినవాడైతే బయలుదేరిన చోటు నుంచి 13 m దూరంలో ఉన్న గుంతలో పడడానికి ఎంత సమయం పడుతుందో గ్రాఫు ద్వారా కనుక్కోండి.
సాధన:
5 అడుగులు ముందుకు నడిస్తే 3 అడుగులు వెనుకకు నడిచాడు. అనగా 8 అడుగులలో నికరస్థానభ్రంశం = 5 – 3 = 2
ఒక అడుగు దూరంలో నడిచినది = 1 మీ.
∴ 8 అడుగులలో నికర స్థానభ్రంశం = 2 మీ.
గుంట దూరము = 13 మీ.
ఒక యత్నంలో ముందుకు వెళ్ళిన దూరం = 5 మీ.
ముందుకు, వెనుకకు నడుస్తూ వెళ్ళవలసినది = 13 – 5 = 8 మీ.
∴ 8 మీ. కొరకు నడవవలసిన అడుగులు = \(\frac{8}{2}\) × 8 = 32
32 అడుగుల తరువాత 5 అడుగులు ముందుకు నడిస్తే అతడు గుంటలో పడిపోతాడు. కాబట్టి గుంటలో పడటానికి వేసిన అడుగులు 32+5=37: ఒక అడుగుకు సమయం = 1 సె.
∴ గుంటలో పడటానికి పట్టిన కాలం 37 × 1 = 37 సె. (బయలుదేరినప్పటి నుండి)

ప్రశ్న 5.
500 km h^-1 వడితో పోతున్న ఒక జెట్ విమానం పరంగా దాని నుంచి దగ్ధం చెందిన ఇంధన వాయువులు 1500 km h^-1 వడితో వెలువడుతున్నాయి. భూమిపై నుంచి పరిశీలించిన వ్యక్తికి వాయువులు ఎంత వడితో వెలువడుతున్నట్లు అనిపిస్తుంది?
సాధన:
విమానం వేగము V = 500 kmph
వాయువుల సాపేక్ష వేగము V_PA = 1500 kmph వ్యతిరేక దిశలో
V_PA = V_P – V_A = – 1500 ⇒ V_P = 500 – 1500 = -1000 kmph
∴ భూమి నుంచి చూస్తే వాయువుల వేగము V_P = 1000 kmph .
– గుర్తు వాయువులు విమాన గమన దిశకు వ్యతిరేకము అని చెపుతుంది.

ప్రశ్న 6.
ఒక తిన్నని రహదారి వెంట ఒక కారు 126 km h^-1 వడిలో ప్రయాణిస్తూ 200m దూరంలో నిశ్చలస్థితిలోకి వచ్చింది. కారు ఋణ త్వరణం (త్వరణం సమరీతి త్వరణం అని భావించండి) ఎంత? నిశ్చలస్థితికి రావడానికి కారు తీసుకొన్న సమయం ఎంత?
సాధన:
తొలివేగము V_o = 126 kmph = 126 × \(\frac{5}{18}\) = 35 మీ/సె.
తుదివేగము V = 0, ఆగిపోవుటకు పట్టిన దూరము x = 200 మీ.
V² – V_o² = 2ax నుండి a = \(\frac{-35^2}{2 \times 200}=\frac{-35 \times 35}{2 \times 200}=\frac{-49}{16}\) = -3.06 మీ/సె²
ఆగిపోవుటకు పట్టిన కాలము t = ?
V = V_o + at నుండి
0 = 35 + \(\frac{49}{16}\) × t
⇒ t = \(\frac{35 \times 16}{49}=\frac{80}{7}\) = 11.43 సె.

ప్రశ్న 7.
400 m పొడవున్న రెండు రైళ్ళు A, B లు రెండు సమాంతర రైలు మార్గాలపై 72 km h^-1 సమవడితో ఒకే దిశలో ప్రయాణిస్తున్నాయి. రైలు A, రైలు B కంటే ముందు ఉన్నది. రైలు B డ్రైవరు, రైలు Aని దాటిపోవాలని నిర్ణయించి తన రైలుకు 1 m s^-2 త్వరణం కలిగించాడు. 50s తరువాత రైలు Bలోని గార్డు, రైలు A డ్రైవరును దాటితే రెండు రైళ్ళ మధ్య ఉన్న అసలు దూరం ఎంత?
సాధన:
A రైలు పొడవు A, = 200 మీ. ; వేగము V_o = 72kmph = \(\frac{72 \times 5}{18}\) = 20 మీ/సె.
త్వరణము a = 0, కాలము t = 50 సె.
X = V_ot + \(\frac{1}{2}\)at² నుండి X_A = 20 × 50 + 0 = 1000 మీ.
B రైలుకు తొలివేగము V_o = 72kmph = 72 × \(\frac{5}{18}\) = 20 మీ/సె.
త్వరణము a = 1 మీ/సె²; కాలము t = 50 సె.
X = V_ot + \(\frac{1}{2}\)at² నుండి X_B = 20 × 50 + \(\frac{1}{2}\) × 1 × 50 × 50
= 1000 + \(\frac{2500}{2}\) = 1000 + 1250 = 2250 మీ.
రైలు B, రైలు A ను దాటడానికి ప్రయాణించవలసిన దూరము
S = రైళ్ళమధ్య దూరము x + A రైలు పొడవు A_o + B రైలుపొడవు B_o
∴ S = x + 400 + 400 కానీ రైళ్ళు ప్రయాణించిన దూరము ‘S’ వాటి సాపేక్ష దూరమునకు సమానము.
∴ S = X_B – X_A = 2250 – 1000 = 1250
∴ 1250 = x + 800
రైళ్ళమధ్య తొలిదూరము x = 1250 – 800 = 450 మీ.

ప్రశ్న 8.
రెండు వరుసలున్న (two-lane) రోడ్డుపై కారు A 36 km h^-1 వడితో పోతున్నది. రెండు కార్లు B, C లు వ్యతిరేక దిశల్లో 54kmh^-1 వడితో A వైపు ప్రయాణిస్తున్నాయి. ఒకానొక క్షణాన, దూరాలు AB, AC లు 1km కు సమానమైనప్పుడు, C కంటే ముందుగా A ని దాటిపోవాలని B నిర్ణయించడం జరిగింది. ప్రమాదాన్ని నివారించడానికి కారు B కి ఉండాల్సిన కనీస త్వరణం ఎంత?
సాధన:
కారు A వేగము 36 kmph = 36 × \(\frac{5}{18}\) =10 మీ/సె.
B మరియు C కార్ల వేగము = 54 kmph = 54 × \(\frac{5}{18}\) = 15 మీ/సె.
A తో పోల్చితే B సాపేక్ష వేగము = 15 – 10 = 5 మీ/సె.
A తో పోల్చితే C సాపేక్ష వేగము = 15 + 10 = 25 మీ/సె. (ఎదురు దశ కావున)
A నుండి B మరియు C ల దూరాలు AB = AC = 1km = 1000 మీ.
C లేదా B కి అందుబాటులో గల కాలవ్యవధి \(\frac{1000}{25}\) = 40 సె.
‘C’ కారు సమీపించే లోపల B అను కారు A ను దాటాలంటే
తొలివేగము V_o = 5 మీ/సె. కాలము t = 40 సె. దూరము x = 1000 మీ.
∴ త్వరణము a = ?; S = V_ot + \(\frac{1}{2}\)at² నుండి
1000 = 5 × 40 + \(\frac{1}{2}\) a × 40 × 40 ⇒ 1000 – 200 + 800a
∴ 800a = 1000 – 200 = 800 లేదా a = 1 మీ/సె²

ప్రశ్న 9.
రెండు పట్టణాలు A, B ల నుంచి ప్రతి T నిమిషాలకు రెండు దిశల్లోనూ బస్సులు బయలుదేరేటట్లు రవాణా సౌకర్యంతో వాటిని సంధానించారు. A నుంచి Bకు 20 km h^-1 వడితో సైకిల్పై ప్రయాణించే వ్యక్తిని, అతని గమన దిశలో, ప్రతి 18 నిమిషాలకు ఒక బస్సు దాటుతుంది. వ్యతిరేక దిశలో ప్రతి 6 నిమిషాలకు ఒక బస్సు దాటుతుంది. రవాణా వ్యవస్థలో రెండు వరుస బస్సుల మధ్య కాలవ్యవధి T, బస్సుల వడి (స్థిర వడిగా భావించండి) ఎంత?
సాధన:
A.B పట్టణాల మధ్య బస్సుల సమవడి = V kmph అనుకోండి.
సైక్లిస్ట్ వేగము = 20 kmph
T కాలంలో బస్ ప్రయాణించిన దూరము = VT
బస్ సాపేక్ష వేగము V_R = (V – 20) kmph
18 ని. ఒక బస్సు వెనుక నుంచి దాటింది అనగా \(\frac{\mathrm{VT}}{\mathrm{V}-20}\) = 18 ⇒ VT = 18(V – 20) → (1)
ఎదురు దిశలో 6 ని. ఒక బస్సు దాటింది అనగా \(\frac{\mathrm{VT}}{\mathrm{V}+20}\) = 6 ⇒ VT= 6(V + 20) → (2)
1, 2 సమీకరణాల నుండి 18(V – 20) = 6(V + 20)
⇒3V – 60 = V + 20 ⇒ 3V – V = 20 + 60
∴ 2V = 80 or V = 40kmph దీనిని సమీకరణం 1 లో రాయగా
40T = 18(40 – 20) ⇒ T = \(\frac{18 \times 20}{40}\) = 9 ని.
∴ బస్సు వేగము V=40kmph
బస్సుల మధ్య కాలవ్యవధి = 9 ని.

ప్రశ్న 10.
ఒక క్రీడాకారుడు ఒక బంతిని 29.4 m s^-1 తొలివేగంతో నిట్టనిలువుగా విసిరాడు.
a) బంతి ఊర్ధ్వ దిశలో గమనంలో ఉన్న కాలంలో త్వరణం దిశ ఏమిటి?
b) బంతి గరిష్ఠ ఎత్తు వద్ద గల బిందువును చేరినప్పుడు బంతి వేగం, త్వరణాల విలువలు ఎంతెంత?
c) బంతి గరిష్ఠ ఎత్తు వద్ద x = 0 m, t = 0 s గా స్థానం, కాలం విలువలను ఎన్నుకొని, నిమ్నదిశను ధన x- దిశగా భావించి, స్థానం, వేగం, త్వరణం సంజ్ఞలను బంతి ఊర్ధ్వ దిశలో గమనంలో ఉన్నప్పుడు, నిమ్న దిశలో గమనంలో ఉన్నప్పుడు ఎలా ఉంటాయో తెలుపండి.
d) బంతి ఎంత ఎత్తుకు చేరుతుందో, ఎంత కాలం తరవాత క్రీడాకారుని చేతిలోకి తిరిగి వస్తుందో తెలుపండి. ( g = 9.8 ms^-2 గాను, గాలి నిరోధం లేనట్లుగానూ భావించండి)
సాధన:
a) వస్తువు గురుత్వాకర్షణ క్షేత్రంలో చలిస్తున్నది కాబట్టి దానిపై త్వరణము ఎల్లపుడు అధోదిశలో ఉంటుంది.
b) గరిష్ఠ స్థానభ్రంశ బిందువు వద్ద వేగము v = 0. కాని త్వరణము a = g = 9.8 మీ/సె. అధోదిశలో

c) గరిష్ఠ స్థానభ్రంశ బిందువు వద్ద x = 0 మరియు t = 0 గా, అధోదిశను X- ధన అక్షంగా తీసుకుంటే అధోదిశలో చలించే వస్తువుకు దాని దిశ ధనాత్మకము, వస్తువు వేగము ధనాత్మకము, త్వరణము ధనాత్మకము.

d) తొలివేగము v₀ = -29.4 మీ/సె. a = 9.8 మీ/సె² v = 0. చేరగల గరిష్ఠ ఎత్తు ‘y’ = ? v² – v₀² = 2ay నుండి
0² – (29.4)² = 2 × 9.8y ⇒ y = \(\frac{-29.4 \times 29.4}{2 \times 9.8}\) = 44.1 మీ.
గరిష్ఠ ఎత్తు చేరటానికి పట్టిన కాలము t = ? v = v₀ + at నుండి 0 = – 29.4 + 9.8t
∴ పైకి పోవుటకు కాలము t = \(\frac{29.4}{-9.8}\) = 3 సె.
వస్తువు మరల చేతిలోనికి రావటానికి పట్టిన కాలము T = 3 + 3 = 6 సె.

ప్రశ్న 11.
కింది వాక్యాలను జాగ్రత్తగా చదివి, అవి తప్పో, ఒప్పో తెలిపి తగిన కారణాలను, ఉదాహరణలను పేర్కొనండి. ఒక కణం ఏకమితీయ గమనంలో ఉంది.
a) ఒకానొక క్షణంలో దాని వడి శూన్యమై, ఆ క్షణంలో త్వరణం శూన్యేతర విలువ కలిగి ఉండవచ్చు.
b) దాని వడి శూన్యమై, వేగం శూన్యేతర విలువ కలిగి ఉండవచ్చు.
c) అది స్థిరవడి కలిగి ఉండి తప్పక త్వరణం శూన్యమై ఉండి తీరాలి.
(d) దాని త్వరణం విలువ ధనాత్మకమై తప్పక వడి వృద్ధి కలిగి ఉండాలి.
సాధన:
a) ఈ వాక్యము నిజమైనది. పైకి విసిరిన వస్తువుకు గరిష్ఠ స్థానభ్రంశ బిందువు వద్ద వడి ‘సున్న’ కాని త్వరణము సున్న కాదు.

b) ఈ వాక్యము తప్పు. వడి సున్న అయినపుడు వేగము సున్న కాకుండా ఉండటానికి వీలులేదు. వడి మరియు వేగముల మధ్య భేదము దిశ ఒక్కటే. కాని పరిమాణము సమానము.

c) ఈ వాక్యము నిజమైనది. వడి స్థిరంగా ఉండి వస్తువు సరళరేఖామార్గంలో ప్రయాణిస్తే దాని త్వరణము తప్పకుండా సున్న అవుతుంది.

d) ఈ వాక్యము నిజమా కాదా అన్నది మనము తీసుకున్న మూల బిందువు నుండి గల దిశపై ఆధారపడుతుంది. వడికి దిశ లేదు. కాబట్టి త్వరణము ఉన్న వస్తువుకు వడి వృద్ధి ఉంటుంది. కాని వస్తువు గమనదిశకు వ్యతిరేకంగా త్వరణదిశ ఉంటే వడిలో వృద్ధి ఉండదు. అనగా వడిలో వృద్ధి ఉండడమా లేదా అన్నది మనం తీసుకున్న నిర్దేశక వ్యవస్థపై ఆధారపడుతుంది.

ప్రశ్న 12.
90 m ఎత్తు నుంచి ఒక బంతిని నేలపైకి జారవిడిచారు. నేలతో అభిఘాతం జరిపిన ప్రతిసారి బంతి తన వేగంలో 10వ వంతు కోల్పోతుంది. t = 0,12s మధ్య బంతి గమనానికి సంబంధించి వడి-కాలం గ్రాఫును గీయండి.
సాధన:
తొలివేగము V = 0
త్వరణము a = g = 10 మీ/సె²
స్థానభ్రంశము y = 90 మీ.
వస్తువు భూమిని తాకటానికి పట్టిన కాలము t = \(\sqrt{\frac{2 \mathrm{y}}{\mathrm{g}}}=\sqrt{\frac{2 \times 90}{10}}=\sqrt{18}\) = 4.24 సె.
భూమిని తాకుటకు ముందు వేగము V =?
V² – V₀² = 2gy నుండి
V = \(\sqrt{2 g y}=\sqrt{2 \times 10 \times 90}=30 \sqrt{2}\) మీ/సె.
ప్రతి అభిఘాతంలో వేగ నష్టము = 10% అనగా V¹ = \(\frac{9}{10}\) v
∴ V¹ = \(\frac{9}{10} \times 30 \sqrt{2}=27 \sqrt{2}\) మీ/సె.

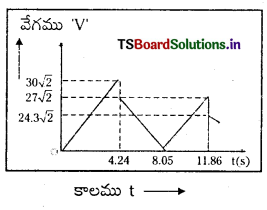
మరల పైకి పోవుటకు పట్టిన కాలము t₁ = \(\frac{\mathrm{V}^1}{\mathrm{a}}=\frac{27 \sqrt{2}}{10}=2.7 \sqrt{2}\) = 3.81
మొత్తం కాలము = 4.24 + 3.81 = 8.05 సె.
వస్తువు మరల 3.81 సెకనులకు కిందపడుతుంది. అనగా మరల 8.05 + 3.81 = 11.86 సెకనులకు నేలను తాకును.
2వ అభిఘాతము పిమ్మట వేగము V¹¹ = \(\frac{9}{10}\) V¹ = \(\frac{9}{10}\)27 \(\sqrt{2}\) = 24.3\(\sqrt{2}\) మీ/సె
అనగా వస్తువు జారవిడిచిన పిమ్మట 4.24 సె.లకు 30\(\sqrt{2}\) మీ/సె వేగంతో నేలకు తాకి 27\(\sqrt{2}\) మీ/సె వేగంతో పైకి లేచి 8.05 సెకనులకు గరిష్ఠ ఎత్తుకు చేరి మరల 11.86 సె. మరల భూమిని తాకుతుంది. ఈ చలనానికి గ్రాఫ్ పై విధంగా ఉంటుంది.

ప్రశ్న 13.
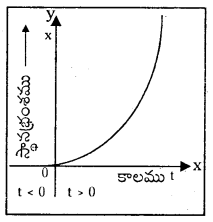
పటంలో ఒక కణం ఏకమితీయ గమనానికి x – t గ్రాఫు చూపడం జరిగింది. గ్రాఫు ద్వారా t < 0 అయినప్పుడు కణం సరళరేఖా మార్గంలో గమనంలో ఉన్నదనీ, t > 0 అయినప్పుడు పరావలయ పథంలో గమనంలో ఉన్నదనీ అనడం సరియైనదేనా? ఒకవేళ సరికాకపోతే, గ్రాఫు సూచించే తగిన భౌతిక సందర్భాన్ని తెలపండి.
సాధన:
కణం సరళరేఖామార్గంలో ఉండదు. ఇచ్చిన స్థానభ్రంశకాల వక్రము సమత్వరణంతో చలించే వస్తువు స్థానభ్రంశాన్ని సూచిస్తుంది. ఈ రేఖాపటము పై నుండి’ స్వేచ్ఛగా కిందికి పడే వస్తువు స్థానభ్రంశ, కాల వక్రాన్ని చూపిస్తుంది.

ప్రశ్న 14.
రహదారిపై 30 km h^-1 వడితో గమనంలో ఉన్న పోలీసు వ్యాను నుంచి అదే దిశలో 192 km h^-1 వడితో కారులో పారిపోతున్న దొంగలపైకి తుపాకీ గుండ్లను పేల్చారు. తుపాకి నుండి వెలువడిన గుండ్ల వడి 150 ms^-1 అయితే, ఎంత వడితో తుపాకి గుండు దొంగల కారును తాకుతుంది? (గమనిక : దొంగల కారుకు హాని చేకూర్చే వడిని రాబట్టండి).
సాధన:
బుల్లెట్ వడి V_B = 150 మీ/సె = 150 × \(\frac{18}{5}\) = 540 kmph
పోలీసు వ్యాన్ వేగము V_P = 30kmph
దొంగ ప్రయాణించే కారు వేగము V_T = 192kmph
చలిస్తున్న కారు నుండి కాల్చడం వల్ల బుల్లెట్ ఫలిత వడి = V_R = V_B + V_P
V_R = 540 + 30 = 570 kmph
దొంగ ప్రయాణించే కారుతో బుల్లెట్ సాపేక్ష వేగము V_BT = V_B – V_T
= 570 – 192 = 378 kmph = \(\frac{378 \times 5}{18}\) = 105m/s.
బుల్లెట్ దొంగల కారును తాకు వేగము = 378 kmph లేదా 105 మీ/సె.

ప్రశ్న 15.
ఒక కణం యొక్క ఏకమితీయ గమనానికి x – t గ్రాఫులో చూపించారు. మూడు వేరు వేరు సమాన కాలవ్యవధులను సూచించారు. ఏ కాలవ్యవధిలో సగటు వడి గరిష్ఠం, ఏ కాలవ్యవధిలో సగటు వడి కనిష్టం? ప్రతి కాలవ్యవధిలో సగటు వేగపు సంజ్ఞను తెలపండి.
సాధన:
స్థానభ్రంశ కాలపు వక్రం వాలు ఇచ్చిన వ్యవధిలో వస్తువుకు గల సగటు వేగాన్ని తెలియజేస్తుంది. ఇచ్చిన పటంలో 3వ కాల వ్యవధి వద్ద రేఖాపటము వాలు గరిష్ఠము కావున దానికి వేగము గరిష్ఠము. ఇది ‘-ve’ గుర్తు కలిగి ఉంటుంది.

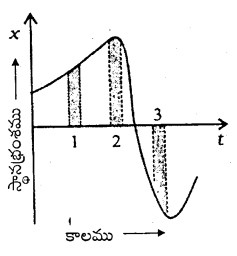
కాలవ్యవధి రెండు వద్ద వాలు అతి తక్కువ కావున ఈ వ్యవధిలో వేగము అతి తక్కువ. ఈ వేగము ధన దిశ కలిగి ఉంది. కాల వ్యవధి ఒకటి వద్ద వేగము ధనాత్మకము. దాని విలువ 2వ వ్యవధి కన్నా ఎక్కువ. కాని 3వ వ్యవధి వేగం కన్నా తక్కువ.

ప్రశ్న 16.
స్థిరమైన (ఒకే) దిశ వెంబడి గమనంలో ఉన్న ఒక కణం గమనానికి వడి – కాలం గ్రాఫును పటంలో చూపించారు. మూడు సమాన కాలవ్యవధులు చూపించారు. ఏ కాలవ్యవధిలో సగటు త్వరణం పరిమాణం గరిష్ఠం? ఏ కాలవ్యవధిలో సగటు వడి గరిష్ఠం? (స్థిర దిశ గల) గమన దిశను ధన దిశగా ఎంచుకుని, v, a ల సంజ్ఞలను మూడు కాలవ్యవధులలోనూ తెలపండి. A, B, C, D బిందువుల వద్ద త్వరణాలు ఏమిటి?
సాధన:
వడి-కాలం యొక్క రేఖాపటపు వాలు కాలవ్యవధిలో వస్తువుకు
గల సమత్వరణాన్ని సూచిస్తుంది. ఇచ్చిన పటంలో
1వ అంతరము వద్ద వడి-కాల వక్రం వాలు ధనాత్మకము కావున త్వరణము ధనాత్మకము మరియు వస్తువు వడి ధనాత్మకము.
2వ కాలవ్యవధి వద్ద వడి కాలము రేఖ వాలు ఋణాత్మకము కావున త్వరణము ఋణాత్మకము కానీ వడి దిశ ధనాత్మకము. (ఎందుకనగా వస్తువు గమన దిశ ‘x+ve’ ను ధనాత్మకంగా
తీసుకున్నాం కావున)

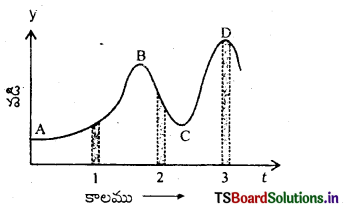
3వ కాలవ్యవధిలో వడి-కాల వక్రం వాలు చాలా ఎక్కువ కావున ఈ అవధిలో త్వరణము గరిష్ఠము వాలు ధనాత్మకం కావున త్వరణము ధనాత్మకము, వడి ధనాత్మకము.
A, B, C, D బిందువులు X- అక్షానికి సమాంతరంగా ఉన్నాయి. కావున ఈ బిందువుల వద్ద త్వరణము a = 0.

ప్రశ్న 17.
నిశ్చలంగా ఉన్న పైకప్పు లేని లిఫ్ట్ లో నిలబడిన ఒక బాలుడు ఒక బంతిని నిట్టనిలువుగా అతడు విసరగలిగిన గరిష్ఠ తొలి వడి 49 m s^-1 తో విసిరాడు. అతని చేతిలోకి తిరిగి చేరడానికి బంతికి ఎంత సమయం పడుతుంది? లిఫ్టు, సమవడి 5 m s^-1 తో పై దిశలో కదులుతూ ఉన్నప్పుడు తిరిగి ఆ బాలుడు అతడు విసరగలిగిన గరిష్ఠ వడితో (49 ms ^-1 ) బంతిని పైకి విసిరితే అతని చేతిలోకి తిరిగి చేరడానికి బంతి తీసుకొనే సమయం ఎంత?
సాధన:
నిట్టనిలువుగా పైకి చలించే దిశను ‘X + ve’ దిశగా తీసుకుంటే
a) లిఫ్ట్ స్థిరంగా ఉన్నపుడు తొలివేగము V_o = 49 మీ/సె. a = -9.8m/s² X – X_o = S = 0 కావున S = V_ot + \(\frac{1}{2}\) gt²
నుండి 0 = 49t + \(\frac{1}{2}\)(-9.8)t² లేదా 4.9t² = 49t అనగా t = \(\frac{49}{4.9}\) = 10 సె.

b) లిఫ్ట్ సమ వేగంతో చలిస్తుంటే త్వరణము a = 0 కావున లిప్పై ఫలితత్వరణము ‘శ్రీ’ కి సమానము. తొలివేగము v_o = 49 మీ/సె, a = g = – 9.8 మీ/సె². కావున ఈ సందర్భంలో కూడా బంతిని పైకి విసిరితే మరలా 10 సెకనులకు చేతిలో పడటం జరుగుతుంది.