TS Inter 1st Year Physics Notes Chapter 4 సమతలంలో చలనం

Here students can locate TS Inter 1st Year Physics Notes 4th Lesson సమతలంలో చలనం to prepare for their exam.

TS Inter 1st Year Physics Notes 4th Lesson సమతలంలో చలనం

→ సదిశ : దిశ, పరిమాణము ఉన్న భౌతిక రాశులను సదిశలు అంటారు.
ఉదా : స్థానభ్రంశము, వేగము, బలము వంటివి.
సదిశలు త్రిభుజ నియమము లేదా సమాంతర చతుర్భుజ సంకలన న్యాయాన్ని పాటించాలి.

→ అదిశ : కేవలం పరిమాణము మాత్రమే ఉండి దిశ లేని రాశులను అదిశలు అంటారు. ఉదా : ద్రవ్యరాశి, వడి, దూరము వంటివి.

→ సదిశల సమానత్వము : రెండు సదిశలు A̅, B̅ లు దిశలోను, పరిమాణంలోను సమానంగా ఉంటే వాటిని సమాన సదిశలు అంటారు.

→ వాస్తవ సంఖ్యలతో సదిశాగుణకారాలు : సదిశలను ఒక ధన సంఖ్య λ చేత గుణించగా లేదా భాగించగా వచ్చే ఫలితం మరల సదిశ అవుతుంది. దాని దిశ మారదు కాని పరిమాణం మారుతుంది.
ఉదా : λ > 0 అయినప్పుడు |λA̅| = λ|A̅|
అనగా A̅ పరిమాణం λ రెట్లు పెద్దది. ఇదే విధంగా
\(\left|\frac{\vec{A}}{\lambda}\right|=\frac{1}{\lambda}|\bar{A}|\) అనగా A̅ పరిమాణం λ రెట్లు చిన్నది.

→ సదిశా సంకలనము : ఒకే తలంలో ఉన్న రెండు సదిశలు A̅, B̅ లను ఒకదాని తల మరొక దాని తోకతో ఏకీభవించే విధంగా జరిపితే అవి ఒక సరళరేఖ వెంబడి లేదా ఒక తలంలో ఉంటాయి.
a) ఒకే సరళరేఖ వెంబడి ఒకే దిశలో ఉంటే ఫలిత సదిశ
R̅ = A̅ + B̅

b) ఒకే సరళరేఖ వెంబడి వ్యతిరేక దిశలో ఉంటే ఫలిత సదిశ

c) ఒకే తలంలో A, B లు ఉంటే త్రిభుజ నియమం లేదా సమాంతర చతుర్భుజ నియమం ద్వారా సంకలనం,
వ్యవకలనం చేయవచ్చు.

→ త్రిభుజ నియమము : రెండు సదిశలను దిశలోను, పరిమాణంలోను ఒక త్రిభుజం యొక్క రెండు భుజాలుగా క్రమపద్ధతిలో సూచిస్తే ఆ త్రిభుజాన్ని పూర్తి చేయడానికి అవసరమైన మూడవ భుజాన్ని వ్యతిరేకదిశలో తీసుకుంటే అది ఫలిత సదిశను దిశలోను, పరిమాణంలోను సూచిస్తుంది.

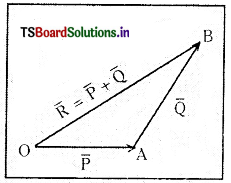
→ సదిశా సంకలన నియమాలు :
1) సదిశా సంకలనము స్థిత్యంతర న్యాయాన్ని పాటిస్తుంది. అనగా A̅ + B̅ = B̅ + A̅
2) సదిశా సంకలనము సహచర న్యాయాన్ని పాటిస్తుంది.
అనగా (A̅ + B̅) + C̅ = A̅ + (B̅ + C̅)

→ ప్రమాణ సదిశ : ఏదైనా సదిశ పరిమాణము ఏకాంకమైతే (1 యూనిట్) దానిని ఏకాంక సదిశ అంటారు.
ప్రమాణ సదిశకు \(\frac{\overline{\mathrm{A}}}{|\overrightarrow{\mathrm{A}}|}\) = 1
Note : ఒక సమతలంలోని X, Y అక్షాల వెంబడి ప్రమాణ దిశలను i̅ మరియు j̅ లతోను, అంతరాళంలోని x, y, z అక్షాల దిశలలోని ప్రమాణ సదిశలను i̅, j̅ మరియు k̅ లతోను సూచిస్తారు.

→ శూన్య సదిశ : పరిమాణము శూన్యమై కేవలం దిశ మాత్రమే కలిగిన రాశిని శూన్య సదిశ అంటారు. దీనిని గె అని సూచిస్తారు.

ఉదా : A̅ – Ā = 0̅ అనగా |0̅| = 0, ఏదైనా సదిశను సున్నతో గుణిస్తే అది శూన్య సదిశ అవుతుంది. Ā × 0 = 0̅

→ స్థాన సదిశ : ఒక సమతలంలోని ఏదైనా సదిశను A̅ = A_xi̅ + A_yj̅ అని, అంతరాళంలో ఏదైనా సదిశను Ā = A_xī + A_yī + A_zk అని సూచిస్తారు. వీటిని స్థాన సదిశలు అంటారు.

→ సమదిశల విభేదనము (Resolution of Vectors) : ప్రతి సదిశను రెండు సదిశలుగా విభేదనం (Resolve) చేయవచ్చు. ఈ మూడు సదిశలు ఒకే సమతలంలో ఉంటాయి. ఈ విభజన ప్రాథమిక త్రికోణమితి నియమాల ఆధారంగా జరుగుతుంది.

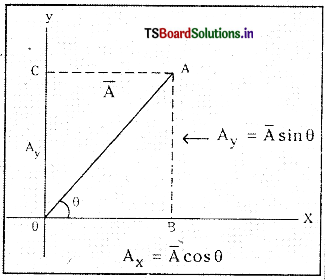
ఉదా : A̅ అను సదిశ X-అక్షంతో ‘θ’ అను కోణం చేస్తుంది.
\(\overline{\mathrm{OB}}\) = A_x = A̅ cos θ;
\(\overline{\mathrm{OC}}=\overrightarrow{\mathrm{B} A}\) = BA = A̅_y = A̅ sin θ

Note : A_x, A_y లను ఇస్తే ఫలిత సదిశ
A̅ = \(\sqrt{A_x^2+A_y^2}\) ఫలిత సదిశ X-అక్షంతో
చేసే కోణము tan θ = \(\frac{A_y}{A_x}\) లేదా θ = tan^-1\(\left[\frac{A_y}{A_x}\right]\)

→ సమాంతర చతుర్భుజ నియమము : ఒక బిందువు వద్ద ఏకకాలంలో పనిచేసే రెండు సదిశలను దిశలోను, పరిమాణంలోను ఒక సమాంతర చతుర్భుజం యొక్క రెండు ఆసన్న భుజాలుగా చూపి ఆ సమాంతర చతుర్భుజాన్ని పూర్తిచేస్తే ఇచ్చిన సదిశల ఖండన బిందువు గుండా పోవు కర్ణము ఫలిత సదిశను దిశలోను,. పరిమాణంలోను సూచిస్తుంది.
ద్విమితీయ చలనము లేదా సమతలంలో చలనము :

→ ద్విమితీయ చలనంలో వస్తువుకు ఏక కాలంలో X-అక్షం వెంబడి మరియు Y-అక్షం వెంబడి చలనం ఉంటుంది. ఏదైనా క్షణంలో వస్తువు యొక్క మొత్తం చలనం X, Y-అక్షములు వెంబడి గల చలన సదిశల మొత్తంగా భావిస్తారు. ఉదా : వస్తువు మొత్తం స్థానభ్రంశము S̅ = S̅_x + S̅_y లేదా r̅ = xi̅ + yj̅

→ వస్తువు గమన పథంపై ఏ బిందువు వద్ద అయినా దాని వేగం అక్కడ గీసిన స్పర్శరేఖ (Tangent) వెంబడి ఉంటుంది.

→ ఏకమితీయ చలనంలో వస్తువు వేగం, త్వరణం ఎల్లపుడూ ఒకే సరళరేఖ వెంబడి సమాంతరంగా కాని లేక వ్యతిరేకంగా కాని ఉంటాయి. కాని ద్విమితీయ చలనంలో వేగము, త్వరణముల మధ్యకోణము 0° నుండి 180° మధ్య ఎంత అయినా ఉండవచ్చు.

→ ద్విమితీయ చలనాన్ని, ఏకకాలంలో రెండు లంబదిశలలో స్థిర వేగము లేదా స్థిర త్వరణము గల రెండు ఏకమితీయ, ఏకకాల చలనాలుగా భావించవచ్చు.

→ ప్రక్షేపకము : ఏదైనా వస్తువును గాలిలోనికి కొంత కోణంతో విసరితే (θ ≠ 90°) దానిని ప్రక్షేపకము అంటారు. ప్రక్షేపకము గమన పథము పరావలయము.
Note : ప్రక్షేపకం గమన పథము y = ax – bx² అనే రెండవ ఘాత రూపంలో ఉంటుంది. ఇటువంటి సమీకరణ గమన పథము పరావలయము.

→ గరిష్టోన్నతి : ప్రక్షేపకం గమన పథం మొత్తంలో క్షితిజ లంబదిశ (y-దిశ) లో గల అత్యధిక స్థానభ్రంశాన్ని గరిపోన్నతి (h_max) అంటారు.
ప్రక్షేపకం గరిష్ఠ ఎత్తు చేరడానికి పట్టే కాలము T = \(\frac{V_0 \sin \theta}{g}\)
గరిష్టాన్నతి h_max = \(\frac{V_0^2 \sin ^2 \theta}{2 g}\)

→ పలాయన కాలము లేదా ప్రక్షేపకం గాలిలో ఉన్న కాలము : వస్తువును గాలిలోనికి విసరిన క్షణం నుండి మరల అది నేలను తాకు వరకు పట్టిన కాలాన్ని పలాయన కాలము లేదా గాలిలో ఉన్న కాలము అంటారు.
పలాయన కాలము T = 2 × గరిష్టోన్నతి కాలము = \(\frac{2 V_0 \sin \theta}{\mathrm{g}}\)

→ క్షితిజ సమాంతర వ్యాప్తి (Range) : వస్తువును గాలిలోనికి ప్రక్షిప్తం చేసిన బిందువు (x + y = 0) నుండి మరల అది క్షితిజ సమాంతర తలాన్ని (y = 0) తాకిన బిందువుకి మధ్యగల దూరాన్ని క్షితిజ సమాంతర వ్యాప్తి అంటారు.
వ్యాప్తి R = \(\frac{2 V_0^2 \sin 2 \theta}{g}\)

→ ఏకరీతి వృత్తాకార చలనము : ఏదైనా వస్తువు స్థిరవడితో వృత్తాకార మార్గం వెంబడి చలిస్తుంటే దానిని ఏకరీతి వృత్తాకార చలనం అంటారు. ఏకరీతి వృత్తాకార చలనంలో వస్తువు వేగం, దిశ నిరంతరం మారుతుంటుంది. కాబట్టి ఆ వస్తువుపై త్వరణం నిరంతరం పని చేస్తుంది.

→ వృత్తాకారచలనంలో వస్తువు వేగము V ఎల్లపుడు వ్యాసార్ధము r కి లంబంగా ఉంటుంది.

→ వృత్తాకారచలనంలో వస్తువుపై V²/R పరిమాణం గల త్వరణం నిరంతరం వృత్త కేంద్రంవైపు పనిచేస్తుంది. దీనిని అభిలంబ త్వరణము అంటారు.
అభిలంబ త్వరణము a_⊥ = V²/R లేదా a_⊥ = ω²R

→ వస్తువు వృత్తాకార మార్గంలో తిరగడానికి ఒక బలం నిరంతరం వృత్త కేంద్రంవైపు పనిచేయాలి. దీనిని అభికేంద్రం బలం అంటారు. అభికేంద్ర బలం = mV²/R

→ భ్రమణ ఆవర్తన కాలము (T) = స్థిరవడితో వృత్త పరిధిపై ఒకసారి పూర్తి భ్రమణం చేయడానికి పట్టిన కాలాన్ని భ్రమణ ఆవర్తన కాలము ‘T’ అంటారు.
Note : పౌనఃపున్యము

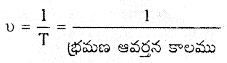
కోణీయ వేగము ω = 2πυ, రేఖీయ వేగము V = 2πυR.

→ ఒకే దిశలో ఉన్న P, Q అను సమాంతర సదిశల ఫలిత సదిశ R = P + Q

→ వ్యతిరేక దిశలో ఉన్న P, Q అను సమాంతర సదిశల ఫలిత సదిశ R = P – Q
Ā అను ఒక సదిశను అంశ సదిశలుగా విభజిస్తే A̅_y = Ā cos θ
A̅_y = A̅ sin θ. ఇందులో ‘θ’ X-అక్షంతో A̅ చేయు కోణము.

→ సమాంతర చతుర్భుజ నియమం నుండి P, Q అను అనుషక్త సదిశల ఫలిత సదిశ R̅ = \(\sqrt{\overline{\mathrm{P}}^2+\overline{\mathrm{Q}}^2+2 \overline{\mathrm{P}} \overline{\mathrm{Q}} \cos \theta}\)
ఫలిత సదిశ (R̅)X-అక్షంతో చేయు కోణము a = tan^-1\(\left[\frac{\overline{\mathrm{Q}} \sin \theta}{\overline{\mathrm{P}}+\overline{\mathrm{Q}} \cos \theta}\right]\)
P̅, Q̅ సదిశల బేధము = R_diff = \(\sqrt{\overline{\mathrm{P}}+\overline{\mathrm{Q}}-2 \overline{\mathrm{P}} \overline{\mathrm{Q}} \cos \theta}\)

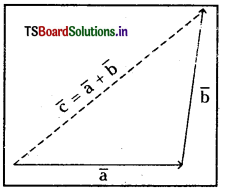
→ a̅, b̅ అను రెండు సదిశలను ఒక త్రిభుజం యొక్క రెండు ఆసన్న భుజాలుగా క్రమపద్ధతిలో
చూపితే ఫలిత సదిశ c̅ = a̅ + b̅

→ రెండు వస్తువులు (A, B) ఒకే దిశలో V_A, V_B వేగాలతో చలిస్తే వాటి సాపేక్ష వేగము V_R = V_A – V_B

→ రెండు వస్తువులు (A. B) వ్యతిరేక దిశలలో V_A, V_B వేగాలతో చలిస్తే సాపేక్ష వేగము = V_R = V_A + V_B

→ నదిని అతి తక్కువ దూరంలో దాటడం : నదిని అతి తక్కువ దూరంలో దాటాలంటే ప్రవాహవేగానికి ఎదురుదిశలో
పడవ నడపవలసిన కోణము θ = sin^-1\(\left[\frac{v_{\mathrm{WE}}}{\mathrm{v}_{\mathrm{BW}}}\right]\)
V_WA : నేల దృష్ట్యా నీటి వేగము ; V_BE : నేల దృష్ట్యా బోటు వేగము

→ నేల దృష్ట్యా బోటు వేగము V_BE = \(\sqrt{\mathrm{V}_{\mathrm{BW}}^2-\mathrm{V}_{\mathrm{WE}}^2}\)
V_BE = నదిలోని నీటితో పోల్చితే బోటు వేగము

→ నదిని దాటడానికి పట్టిన కాలము t

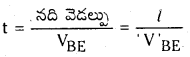
→ నదిని అతి తక్కువ కాలంలో దాటడం :
నదిని దాటడానికి పట్టిన కాలము

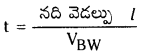
V_BE = ప్రవాహంతో పోలిస్తే బోటు వేగము

→ బోటు ఫలిత వేగము V_R = \(\sqrt{\mathrm{v}_{\mathrm{BW}}^2-\mathrm{v}_{\mathrm{WE}}^2}\)

→ ప్రవాహదిశతో బోటు చేయు కోణము θ = tan^-1\(\left[\frac{V_{\mathrm{WE}}}{\mathrm{V}_{\mathrm{BE}}}\right]\)

→ ప్రక్షేపకాలలో
ఒక వస్తువును క్షితిజ సమాంతర దిశతో ‘θ’ కోణం చేస్తూ ప్రక్షేపించబడిన, ప్రక్షేపకం యొక్క వేగం క్షితిజ సమాంతర అంశం u_x = u cos θ. u_x విలువ, చలనం అంతటా స్థిరంగా ఉండిపోతుంది.

→ వేగం యొక్క లంబ అంశము u_y = u sin θ. ఈ అంశము కాలముతో పాటు మారుతుంది.

→ ప్రయాణకాలం T = \(\frac{2 \mathrm{u} \sin \theta}{\mathrm{g}}\), గరిష్ఠ ఎత్తు H_max = \(\frac{\mathrm{u}^2 \sin ^2 \theta}{2 \mathrm{~g}}\), క్షితిజ సమాంతర వ్యాప్తి R = \(\frac{\mathrm{u}^2 \sin 2 \theta}{\mathrm{g}}\)

→ t సెకనుల తరువాత, ప్రక్షేపక వేగం v = \(\sqrt{v_x^2+v_y^2}\); v_x = u_x = u cos θ మరియు v_x = u sin θ – gt

→ వేగ సదిశ ‘v’ క్షితిజ సమాంతరంతో చేయు కోణం α = tan^-1\(\left[\frac{v_y}{v_x}\right]\) v_y = u sin θ – gt మరియు v_x = u cos θ.

→ ప్రక్షిప్త కోణాలు θ మరియు (90- θ) లకు క్షితిజ సమాంతర వ్యాప్తి సమానము. θ = 45° అయిన వ్యాప్తి గరిష్ఠము.
R_max = \(\frac{u^2}{\mathrm{~g}}\) మరియు h_max = \(\frac{\mathrm{u}^2}{4 \mathrm{~g}}\)

→ R_max మరియు h_max ల మధ్య సంబంధము R_max = 4 h_max

→ పూరక కోణాల ఎత్తులు h₁ మరియు h₂ అయిన h₁ + h₂ = \(\frac{u^2}{4 \mathrm{~g}}\); R = 4\(\sqrt{\mathrm{h}_1 \mathrm{~h}_2}\); R_max = 2(h₁ + h₁)

→ క్షితిజ సమాంతర ప్రక్షేపకం యొక్క అవరోహణ కాలం t = \(\sqrt{\frac{2 \mathrm{~h}}{\mathrm{~g}}}\)

→ క్షితిజ సమాంతర ప్రక్షేపకం యొక్క వ్యాప్తి R = u × t = u\(\sqrt{\frac{2 \mathrm{~h}}{\mathrm{~g}}}\).

→ కాలం ‘t’ సెకనుల తరువాత ప్రక్షేపకం వేగము v = \(\sqrt{v_x^2+v_y^2}\)
ఇందులో v_x = u_x : v_x = gt
v = \(\sqrt{\mathrm{u}^2+\mathrm{g}^2 \mathrm{t}^2}\)

→ వేగ సదిశ ‘v’, x-అక్షముతో చేయు కోణం α = tan^-1\(\left[\frac{v_y}{v_x}\right]\) కాని v_x = u, v_y = gt
∴ α = tan^-1\(\left[\frac{\mathrm{gt}}{\mathrm{u}}\right]\)