TS 10th Class Maths Solutions Chapter 5 Quadratic Equations Ex 5.4

Students can practice 10th Class Maths Solutions Telangana Chapter 5 Quadratic Equations Ex 5.4 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 5 Quadratic Equations Exercise 5.4

Question 1.
Find the nature of the roots of the following quadratic equations. If real roots exist, find them. (A.P June is)

i) 2x² – 3x + 5 = 0
Solution:
Given : 2x² – 3x + 5 = 0
a = 2; b = -3; c = 5
Discriminant = b² – 4ac
b² – 4ac = (-3)² – 4(2)(5)
= 9 – 40
= -31 < 0
Roots are imaginary,

ii) 3x² – 4 \(\sqrt{3}\)x + 4 = 0
Solution:
Given : 3x² – 4\(\sqrt{3}\)x + 4 = 0
a = 3; b = -4\(\sqrt{3}\) ; c = 4
b² – 4ac = (-\(\sqrt{3}\))² – 4(3)(4)
= 48 – 48 = 0
∴ Roots are real and equal and they are
\(\frac{-b}{2 a}\), \(\frac{-b}{2 a}\)
= \(\frac{-(-4 \sqrt{3})}{2 \times 3}\) = \(\frac{4 \sqrt{3}}{6}\) = \(\frac{2}{\sqrt{3}}\), \(\frac{2}{\sqrt{3}}\)

iii) 2x² – 6x + 30
Solution:
Given : 2x² – 6x + 3 = 0
a = 2; b = -6; c = 3
b² – 4ac = (-6)² – 4(2)(3)
= 36 – 24 = 12 > 0
The roots are real and distinct.
They are

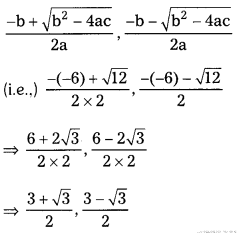
Question 2.
Find the values of k for each of the following quadratic equations so that they have two equal roots.

i) 2x² + kx + 3 = 0
Solution:
Given : 2x² + kx + 3 = 0 has equal roots
∴ b² – 4ac = 0
Here a = 2; b = k; c = 3
b² – 4ac = (k)² – 4(2) (3) = 0
⇒ k² – 24 = 0
⇒ k² = 24
⇒ k = \(\sqrt{24}\)
= ±2 \(\sqrt{6}\)

ii) kx(x – 2) + 6 = 0
Solution:
Given : kx(x – 2) + 6 = 0
kx² – 2kx + 6 = 0
As this Q.E. has equal roots.
b² – 4ac = 0
Here a = k; b = -2k; c = 6
∴ b² – 4ac = (-2k)² – 4(k) (6) = 0
⇒ 4k² – 24 k = 0
⇒ 4k(k – 6) = 0
⇒ k = 0 (or) k – 6 = 0
⇒ k = 0 (or) 6
But k = 0 is trivial
∴ k = 6

Question 3.
Is it possible to design a rectangular mango grove whose length is twice its breadth, and the area is 800 m² ? If so, find its length and breadth. (A.P. June 15)
Solution:
Let the breadth = x m
Then length = 2x m
Area = length × breadth
= x. (2x) = 2x² m²
By problem 2x² = 800
⇒ x² = 400
and x = \(\sqrt{400}\) = ± 20
∴ Breadth x = 20 m and
Length 2x = 2 × 20 = 40 m

Question 4.
The sum of the ages of two friends is 20 years. Four years ago, the product of their ages in years was 48. Is the situation possible ? If so, determine their present ages.
Solution:
Let the age one of the two friends be x years.
Then the age of the other = 20 – x
Then, 4 years ago their ages would be (x – 4) and (20 – x – 4) = 16 – x
∴ Problem (x – 4) (16 – x) = 48
⇒ x(16 – x) – 4(16 – x) = 48
⇒ 16x – x² – 64 + 4x = 48
⇒ x² – 20x + 112 = 0
Here a = 1; b = – 20; c = 112
b² – 4ac = (-20)² – 4(1) (112)
= 400 – 448 = -48 < 0
Thus the roots are not real.
∴ The situation is not possible.

Question 5.
Is it possible to design a rectangular park of perimeter 80m and area 400m² ? If so, find its length and breadth.
Solution:
Given : Perimeter of a rectangle 2(1l + b) = 80
⇒ l + b = \(\frac{80}{2}\) = 40 —– (1)
Area of the rectangle, l × b = 400
It possible, let us suppose that length of the rectangle = x m say
Then its breadth by equation (1) = 40 – x
By problem area = x. (40 – x) = 400
⇒ 40x – x² = 400
⇒ x² – 40x + 400 = 0
Here a = 1; b = – 40; c = 400
b² – 4ac = (-40)² – 4(1)(400)
= 1600 – 1600
= 0
∴ The roots are real and equal.
They are \(\frac{-b}{2 a}\), \(\frac{-b}{2 a}\)
i.e., \(\frac{-(-40)}{2 \times 1}\) = \(\frac{40}{2}\) = 20
∴ The dimensions are 20m, 20m.
(∴ The park is in square shape)