Students can practice 10th Class Maths Solutions Telangana Chapter 4 Pair of Linear Equations in Two Variables Ex 4.3 to get the best methods of solving problems.
TS 10th Class Maths Solutions Chapter 4 Pair of Linear Equations in Two Variables Exercise 4.3
Question 1.
Solve each of the following pairs of equations by reducing them to a pair of linear equations. (T.S. Mar. 15) (A.P. Mar. 15)
i) \(\frac{5}{x-1}\) + \(\frac{1}{y-2}\) = 2
\(\frac{6}{x-1}\) – \(\frac{3}{y-2}\) = 1
Solution:
Given, \(\frac{5}{x-1}\) + \(\frac{1}{y-2}\) = 2 and
\(\frac{6}{x-1}\) – \(\frac{3}{y-2}\) = 1
Put \(\frac{1}{x-1}\) = a and \(\frac{1}{y-2}\) = b,
then the given equations reduce to
5a + b = 2 —– (1)
6a – 3b = 1 —– (2)
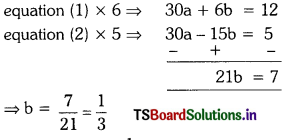
Substituting b = \(\frac{1}{3}\) in equation(1), we get
5a + \(\frac{1}{3}\) = 2 ⇒ 5a = 2 – \(\frac{1}{3}\)
⇒ 5a = \(\frac{3 \times 2-1}{3}\)
⇒ 5a = \(\frac{6-1}{3}\)
∴ a = \(\frac{5}{3}\) × \(\frac{1}{5}\) = \(\frac{1}{3}\)
But a = \(\frac{1}{x-1}\) ⇒ \(\frac{1}{3}\) = \(\frac{1}{x-1}\)
⇒ (x – 1) . 1 = 3 x 1
x – 1 = 3 ⇒ x = 3 + 1 = 4
b = \(\frac{1}{y-2}\) ⇒ \(\frac{1}{3}\) = \(\frac{1}{y-2}\)
⇒ y – 2 = 3 ⇒ y = 3 + 2 = 5
∴ Solution (x, y) = (4, 5)
ii) \(\frac{x+y}{x y}\) = 2, \(\frac{x-y}{x y}\) = 6
Solution:
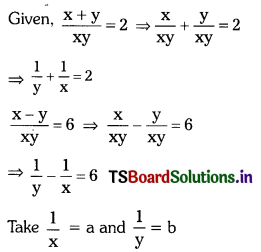
Then the given equations reduces to
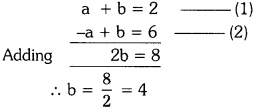
Substituting b = 4 in equation (1), we get
a + 4 = 2 ⇒ a = 2 – 4 = -2
But a = \(\frac{1}{x}\) = -2 ⇒ x = \(\frac{-1}{2}\)
b = \(\frac{1}{y}\) = 4 ⇒ y = \(\frac{1}{4}\)
∴ The solution (x, y) = \(\left[\frac{-1}{2}, \frac{1}{4}\right]\)
![]()
iii) \(\frac{2}{\sqrt{x}}\) + \(\frac{3}{\sqrt{y}}\) = 2; \(\frac{4}{\sqrt{x}}\) – \(\frac{9}{\sqrt{y}}\) = -1
Solution:
Given, \(\frac{2}{\sqrt{x}}\) + \(\frac{3}{\sqrt{y}}\) = 2 and \(\frac{4}{\sqrt{x}}\) – \(\frac{9}{\sqrt{y}}\) = -1
Take \(\frac{1}{\sqrt{x}}\) = a and \(\frac{1}{\sqrt{y}}\) = a
Then the given equations reduce to
2a + 3b = 2 —- (1)
4a – 9b = – 1 —– (2)

Substituting, b = \(\frac{1}{3}\) in equation (1), we get

iv) 6x + 3y = 6xy
2x + 4y = 5xy
Solution:
Given, 6x + 3y = 6xy
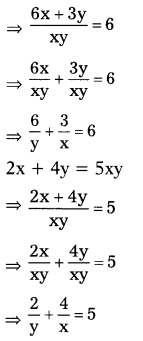
Take \(\frac{1}{x}\) = a and \(\frac{1}{y}\) = b
3a + 6b = 6 —– (1)
4a + 2b = 5 —- (2)

v) \(\frac{5}{x+y}\) – \(\frac{2}{x-y}\) = -1, \(\frac{15}{x+y}\) + \(\frac{7}{x-y}\) = 10 where x ≠ 0, y ≠ 0.
Solution:
Given, \(\frac{5}{x+y}\) – \(\frac{2}{x-y}\) = -1 and \(\frac{15}{x+y}\) + \(\frac{7}{x-y}\) = 10
Take \(\frac{1}{x+y}\) = a and \(\frac{1}{x-y}\) = b, then the given equations reduce to
5a – 2b = -1 —— (1)
15a + 7b = 10 —- (2)

Substituting b = 1 in equation (1), we get
5a – 2(1) = -1 ⇒ 5a = -1 + 2
5a = 1 ⇒ a = \(\frac{1}{5}\)
But a = \(\frac{1}{x+y}\) = \(\frac{1}{5}\) ⇒ x + y = 5
b = \(\frac{1}{x-y}\) = 1 ⇒ x – y = 1
Solving the above equations
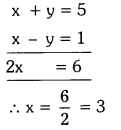
Substituting x = 3 in x + y = 5, we get
3 + y = 5 ⇒ y = 5 – 3 = 2
∴ The solution (x, y) = (3, 2)
vi) \(\frac{2}{x}\) + \(\frac{3}{y}\) = 13; \(\frac{5}{x}\) – \(\frac{4}{y}\) = -2 where x ≠ 0, y ≠ 0. (A.P. Jun. 15)
Solution:
Given, \(\frac{2}{x}\) + \(\frac{3}{y}\) = 13 and \(\frac{5}{x}\) – \(\frac{4}{y}\) = -2
Put \(\frac{1}{x}\) = a and \(\frac{1}{y}\) = b
Then the given equations reduce to
2a + 3b = 13 —– (1)
5a – 4b = -2 —– (2)
Solving (1) & (2), we get

Substituting b = 3 in equation (1), we get
2a + 3(3) = 13 ⇒ 2a = 13 – 9
⇒ a = \(\frac{4}{2}\) = 2
But, a = \(\frac{1}{x}\) = 2 ⇒ x = \(\frac{1}{2}\)
b = \(\frac{1}{y}\) = 3 ⇒ y = \(\frac{1}{3}\)
∴ The solution (x, y) = \(\left(\frac{1}{2}, \frac{1}{3}\right)\)
vii) \(\frac{10}{x+y}\) + \(\frac{2}{x-y}\) = 4; \(\frac{15}{x+y}\) – \(\frac{5}{x-y}\) = -2
Solution:
Given, \(\frac{10}{x+y}\) + \(\frac{2}{x-y}\) = 4; \(\frac{15}{x+y}\) – \(\frac{5}{x-y}\) = -2
Taking \(\frac{1}{x+y}\) = a and \(\frac{1}{x-y}\) = b then the given equations reduce to
10a + 2b = 4 —– (1)
15a – 5b = -2 —- (2)
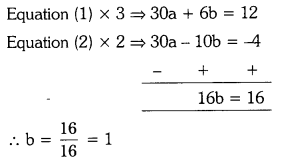
Substituting b = 1 in equation (1), we get 10a + 2(1) = 4
⇒ 10a = 4 – 2 ⇒ a = \(\frac{2}{10}\) = \(\frac{1}{5}\)

Substituting x = 3 in x + y = 5, we get
3 + y = 5 ⇒ y = 5 – 3 = 2
∴ The solution (x, y) = (3, 2)
viii) \(\frac{1}{3 x+y}\) + \(\frac{1}{3 x-y}\) = \(\frac{3}{4}\)
\(\frac{1}{2(3 x+y)}\) – \(\frac{1}{2(3 x-y)}\) = \(\frac{-1}{8}\)
Solution:
\(\frac{1}{3 x+y}\) + \(\frac{1}{3 x-y}\) = \(\frac{3}{4}\) and \(\frac{1}{2(3 x+y)}\) – \(\frac{1}{2(3 x-y)}\) = \(\frac{-1}{8}\)
Take \(\frac{1}{3 x+y}\) = a; \(\frac{1}{3 x-y}\) = b,
then the given equations reduce to

Sustituting a = \(\frac{1}{4}\) in equation (1), we get
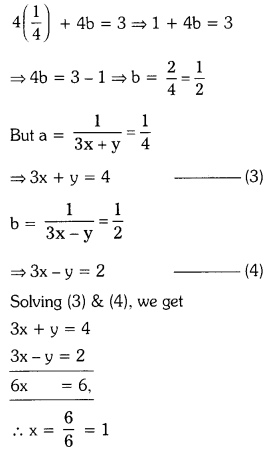
Substituting x = 1 in 3x + y = 4
⇒ 3(1) + y = 4 ⇒ y = 4 – 3 = 1
∴ The solution (x, y) = (1, 1)
![]()
Question 2.
Formulate the following problems as a pair of equations and then find their solutions.
i) A boat goes 30 km upstream and 44 km downstream in 10 hours. In 13 hours it can go 40 km upstream and 55 km downstream. Determine the speed of the stream and speed of the boat in still water.
Solution:
Let, the speed of the boat in still water = x kmph
and the speed of the stream = y kmph.
then speed in downstream = x + y Speed in upstream = x – y

then the above equations reduce to
30a + 44b = 10 —– (1)
40a + 55b = 13 —- (2)

Substituting b = \(\frac{1}{11}\) in equation (1), we get
30a + 44(\(\frac{1}{11}\)) = 10
⇒ 30a = 10 – 4 ⇒ a = \(\frac{6}{30}\) = \(\frac{1}{5}\)
but a = \(\frac{1}{x-y}\) = \(\frac{1}{5}\) ⇒ x – y = 5 —- (3)
b = \(\frac{1}{x+y}\) = \(\frac{1}{11}\) ⇒ x + y = 11 —- (4)
Adding (3) and (4)
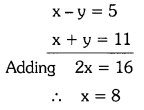
Substituting x = 8 in x – y = 5, we get
8 – y = 5 ⇒ y = 8 – 5 = 3
∴ The solution (x, y) = (8, 3)
Speed of the boat in still water = 8 kmph
Speed of the stream = 3kmph
![]()
ii) Rahim travels 600 km to his home partly by train and partly by car. He takes 8 hours If he travels 120 km by train and rest by car. He takes 20 minutes more If he travels 200 km by train and rest by car. Find the speed of the train and the car.
Solution:
Let, the speed of the train be x kmph, and the speed of the car be y kmph
By problem,

then the equations reduce to
15a + 60b = 1 —- (1)
8a + 16b = \(\frac{1}{3}\) ⇒ 24a + 48b = 1 —- (2)

Substituting a = \(\frac{1}{36}\) in Equation (1)
we get,
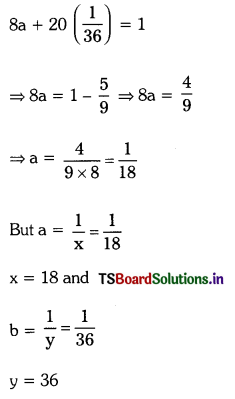
∴ Time taken by 1 woman 18 days
Time taken by 1 man = 36 days