TS 10th Class Maths Solutions Chapter 5 Quadratic Equations Ex 5.2

Students can practice 10th Class Maths Solutions Telangana Chapter 5 Quadratic Equations Ex 5.2 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 5 Quadratic Equations Exercise 5.2

Question 1.
Find the roots of the following quadratic equations by factorisation.

i) x² – 3x – 10 = 0
Solution:
Given : x² – 3x – 10 = 0
⇒ x² – 5x + 2x – 10 = 0
⇒ x(x – 5) + 2 (x – 5) = 0
⇒ (x – 5) (x + 2) = 0
⇒ x – 5 = 0 or x + 2 = 0
⇒ x = 5 or x = -2
⇒ x = 5 or – 2
are the roots of the given Q.E.

ii) 2x² + x – 6 = 0 (A.P.Mar. 16)
Solution:
Given : 2x² + x – 6 = 0
⇒ 2x² + 4x – 3x – 6 = 0
⇒ 2x(x + 2) – 3(x + 2) = 0
⇒ (x + 2) (2x – 3) = 0
⇒ x + 2 = 0 or 2x – 3 = 0
⇒ x = -2 or 2x = 3
⇒ x = -2 or \(\frac{3}{2}\)
are the roots of the given Q.E.

iii) \(\sqrt{2}\)x² + 7x + 5\(\sqrt{2}\) = 0
Solution:
Given : \(\sqrt{2}\)x² + 7x + 5\(\sqrt{2}\) = 0
⇒ \(\sqrt{2}\)x² + 5x + 2x + 5\(\sqrt{2}\) = 0
⇒ x(\(\sqrt{2}\)x + 5) + \(\sqrt{2}\)(\(\sqrt{2}\)x + 5) = 0
⇒ (\(\sqrt{2}\)x + 5)(x + \(\sqrt{2}\)) = 0
⇒ \(\sqrt{2}\)x + 5 = 0 or x + \(\sqrt{2}\) = 0
⇒ \(\sqrt{2}\)x = – 5 or x = –\(\sqrt{2}\)
⇒ x = \(\frac{-5}{\sqrt{2}}\) or –\(\sqrt{2}\) are the roots of the given Q.E.

iv) 2x² – x + \(\frac{1}{8}\) = 0
Solution:
Given : 2x² – x + \(\frac{1}{8}\) = 0
⇒ \(\frac{16 x^2-8 x+1}{8}\) = 0
⇒ 16x² – 8x + 1 = 0
⇒ 16x² – 4x – 4x + 1 = 0
⇒ 4x(4x – 1) – 1(4x – 1) = 0
⇒ (4x – 1) (4x- 1) = 0
⇒ 4x – 1 = 0
⇒ 4x = 1
⇒ x = \(\frac{1}{4}\), \(\frac{1}{4}\)
are the roots of given Q.E.

v) 100x² – 20x + 1 = 0
Solution:
Given : 100x² – 20x + 1 = 0
⇒ 100x² – 10x – 10x + 1 = 0
⇒ 10x (10x – 1) – 1(10x – 1) = 0
⇒ (10x – 1) (10x – 1) = 0
⇒ 10x – 1 = 0
⇒ 10x = 1
x = \(\frac{1}{10}\), \(\frac{1}{10}\)
are the roots of the given Q.E.

vi) x(x + 4) = 12
Solution:
Given : x(x + 4) = 12
⇒ x² + 4x = 12
⇒ x² + 4x – 12 = 0
⇒ x² + 6x – 2x – 12 = 0
⇒ x(x + 6) – 2(x + 6) = 0
⇒ (x + 6) (x – 2) = 0
⇒ x + 6 = 0 or x – 2 = 0
⇒ x = -6 or x = 2
⇒ x = -6 or 2
are the roots of the given Q.E.

vii) 3x² – 5x + 2 = 0
Solution:
Given : 3x² – 5x + 2 = 0
⇒ 3x² – 3x – 2x + 2 = 0
⇒ 3x(x – 1) – 2(x – 1) = 0
⇒ (x – 1) (3x – 2) = 0
⇒ x – 1 = 0 or 3x – 2 = 0
⇒ x = 1 or x = \(\frac{2}{3}\)
⇒ x = 1 or \(\frac{2}{3}\)
are the roots of the given Q.E.

viii) x – \(\frac{3}{x}\) = 2
Solution:
Given : x – \(\frac{3}{x}\) = 2
⇒ \(\frac{x^2-3}{x}\) = 2
⇒ x² – 3 = 2x
⇒ x² – 2x – 3 = 0
⇒ x² – 3x + x – 3 = 0
⇒ x(x – 3) + 1(x – 3) = 0
⇒ (x – 3) (x + 1) = 0
⇒ x = 3 or x = -1
⇒ x = 3 or – 1
are the roots of the given Q.E.

ix) 3(x – 4)² – 5(x – 4) = 12
Solution:
Take (x -4) = a, then the given Q.E.
⇒ reduces to 3a² – 5a = 12
⇒ 3a² – 5a – 12 = 0
⇒ 3a² – 9a + 4a – 12 = 0
⇒ 3a(a – 3) + 4(a – 3) = 0
⇒ (a – 3) (3a + 4) = 0 = 0
⇒ a – 3 = 0 or 3a + 4 = 0
⇒ a = 3 or a = \(\frac{-4}{3}\)
but a = x – 4
∴ x – 4 = 3 (or) x – 4 = \(\frac{-4}{3}\)
⇒ x = 7 or x = 4 – \(\frac{4}{3}\)
⇒ x = 7 or \(\frac{8}{3}\)
are the roots of the given Q.E.

Question 2.
Find two numbers whose sum is 27 and product is 182. (A.P.Mar. 15)
Solution:
Let a number be x.
Then the other number = 27 – x
Product of the numbers = x(27 – x)
= 27x – x²
By problem 27x – x² = 182
⇒ x² – 27x + 182 = 0
⇒ x² – 14x – 13x + 182 = 0
⇒ x(x – 14) – 13(x – 14) = 0
⇒ (x – 13) (x – 14) = 0
⇒ x – 13 = 0 or x – 14 = 0
⇒ x = 13 or 14.
The numbers are 13; 27 – 13 = 14 or 14 and 27 – 14 = 13.

Question 3.
Find two consecutive positive integers, sum of whose squares is 613.
Solution:
Let a positive integer be x.
Then the second integer = x + 1
Sum of the squares of the above integers = x² + (x + 1)²
= x² + x² + 2x + 1
= 2x² + 2x + 1
By problem 2x² + 2x + 1 = 613
⇒ 2x² + 2x – 612 = 0
⇒ x² + x – 306 = 0
⇒ x² + 18x – 17x – 306 = 0
⇒ x(x + 18) – 17(x + 18) = 0
⇒ (x – 17) (x + 18) = 0
⇒ x – 17 = 0 (or) x + 18 = 0
⇒ x = 17 (or) -18
Then the numbers are x = (17; 17 + 1) or x = (-18; -18 + 1)
i.e., 17, 18 or -17, -18.

Question 4.
The altitude of a right triangle is 7cm less than its base. If the hypotenuse is 13cm, find the other two sides.
Solution:
Let the base of the right triangle = x cm
Then its altitude = x – 7 cm
By Pythagoras Theorem

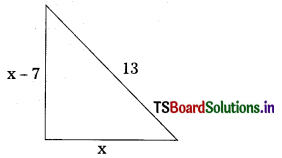
(base)² + (height)² = (hypotenuse)²
⇒ x² + (x – 7)² = 13²
⇒ x² + x² – 14x + 49 = 169
⇒ 2x² – 14x + 49 – 169 = 0
⇒ 2x² – 14x – 120 = 0
⇒ x² – 7x – 60 = 0
⇒ x² – 12x + 5x – 60 = 0
⇒ x(x – 12) + 5(x – 12) = 0
⇒ (x – 12)(x + 5) = 0
⇒ x = 12 (or) x = – 5
But x can’t be negative.
∴ x = 12
x – 7 = 12 – 7 = 5
The two sides are 12 cm and 5 cm.

Question 5.
A cottage industry produces a certain number of pottery articles in a day. It was observed in a particular day that the cost of production of each article (in rupees) was 3 more than twice the number of articles produced on that day. if the total cost of production on that day was ₹ 90, find the number of articles produced and the cost of each article.
Solution:
Let the number of articles produced be x.
Then the cost of each article = 2x + 3
Total cost of the articles produced = x[2x + 3] = 2x² + 3x
By problem 2x² + 3x = 90
⇒ 2x² + 3x – 90 = 0
⇒ 2x² + 15x – 12x – 90 = 0
⇒ x(2x + 15) – 6(2x + 15) = 0
⇒ (2x + 15) (x – 6) = 0
⇒ 2x + 15 = 0 (or) x – 6 = 0
⇒ x = \(\frac{-15}{2}\) or x = 6
But x can’t be negative, x = 6
∴ x = 6
2x + 3 = 2 × 6 + 3 = 15
∴ Number of articles produced = 6
Cost of each article = ₹ 15.

Question 6.
Find the dimensions of a rectangle whose perimeter is 28 meters and whose area is 40 square meters.
Solution:
Let the length of the rectangle = x
Given perimeter = 2(l + b) = 28
⇒ l + b = \(\frac{28}{2}\) = 14
∴ Breadth of the rectangle = 14 – x
Area = Length × Breadth = x(14 – x)
= 14x – x²
By problem, 14x – x² = 40
⇒ x² – 14x + 40 = 0
⇒ x² – 10x – 4x + 40 = 0
⇒ x(x – 10) – 4(x – 10) = 0
⇒ (x – 10) (x – 4) = 0
⇒ x – 10 = 0 (or) x – 4 = 0
⇒ x = 10 (or) 4
∴ Length = 10 m or 4 m
Then breadth 14 – 10 = 4 m (or) = 14 – 4 = 10 m

Question 7.
The base of a triangel is 4 cm longer than its altitude. If the area of the triangle is 48 sq.cm, then find its base and altitude.
Solution:
Let the altitude of the triangle h = x cm
Then its base ‘b’ = x + 4
Area = \(\frac{1}{2}\) × base × height
= \(\frac{1}{2}\)(x + 4)(x) = \(\frac{x^2+4 x}{2}\)
By problem \(\frac{x^2+4 x}{2}\) = 48
⇒ x² + 4x = 2 × 48
⇒ x² + 4x – 96 = 0
⇒ x² + 12x – 8x – 96 = 0
⇒ x(x + 12) – 8(x + 12) = 0
⇒ (x + 12) (x – 8) = 0
⇒ x + 12 = 0 (or) x – 8 = 0
⇒ x = -12 (or) x = 8
But x can’t be negative.
∴ x = 8 and x + 4 = 8 + 4 = 12
Hence altitude = 8 cm and base = 12 cm.

Question 8.
Two trains leave a railway station at the same time. The first train travels towards west and the second train towards north. The first train travels 5 km/hr faster than the second train. If after two hours they are 50 km. apart, find the average speed of each train.
Solution:
Let the speed of the slower train = x kmph
Then speed of the faster train = x + 5 kmph
Distance = Speed × Time
Distance travelled by the first train = 2(x + 5) = 2x + 10
Distance travelled by the second train = 2.x = 2x
By Pythagoras Theorem
(hypotenuse)² = (side)² + (side)²
⇒ (2x)² + (2x + 10)² = 50²
⇒ 4x² + (4x² + 40x + 100) = 2500
⇒ 4x² + 4x² + 40x + 100 = 2500
⇒ 8x² + 40x – 2400 = 0
⇒ x² + 5x – 300 = 0
⇒ x² + 20x – 15x – 300 = 0
⇒ x(x + 20) – 15(x + 20) = 0
⇒ (x + 20) (x – 15) = 0
∴ x – 15 = 0 (or) x + 20 = 0
⇒ x = 15 (or) x – 20
⇒ x = 15 (or) – 20
But x can’t be negative.
∴ Speed of the slower train x = 15 kmph.
Speed of the faster train x + 5 = 15 + 5 = 20 kmph.

Question 9.
In a class of 60 students, each boy contributed rupees equal to the number of girls and each girl contributed rupees equal to the number of boys. If the total money then collected was ₹ 1600, how many boys are there in the class ?
Solution:
Let the number of boys in the class = x
Then number of girls in the class = 60 – x [∵ total students = 60]
Money contributed by the boys = x(60 – x) = 60x – x² [∵ given]
Money contributed by the girls = (60 – x) x = 60x – x²
Money contributed by the class = 120x – 2x²
By problem 120x – 2x² = 1600
⇒ x² – 60x + 800 = 0
⇒ x² – 40x – 20x + 800 = 0
⇒ x(x – 40) – 20(x – 40) = 0
⇒ (x – 40) (x – 20) = 0
⇒ x = 40 (or) 20
∴ Boys = 40 or 20
Girls = 20 or 40.

Question 10.
A motor boat heads upstream a distance of 24 km on a river whose current is running at 3 km per hour. The trip up and back takes 6 hours. Assuming that the motor boat maintained a constant speed, what was its speed ?
Solution:
Let the speed of the boat in still water be x kmph.
Speed of the current = 3 kmph
Then speed of the boat in upstream = (x – 3)kmph
Speed of the boat in down stream = (x + 3) kmph
By problem total time taken = 6hrs
∴ \(\frac{24}{x-3}\) + \(\frac{24}{x+3}\) = 6
⇒ 24[\(\frac{1}{x-3}\) + \(\frac{1}{x+3}\)] = 6
⇒ 24\(\left[\frac{x+3+x-3}{(x+3)(x-3)}\right]\) = 6
⇒ 24(2x) = 6(x² – 9)
⇒ 8x = x² – 9
⇒ x² – 8x – 9 = 0
⇒ x² – 9x + x – 9 = 0
⇒ x(x – 9) + 1(x – 9) = 0
⇒ (x – 9) (x + 1) = 0
⇒ x – 9 = 0 or x + 1 = 0
x can’t be negative.
∴ x = 9
i.e., speed of the boal in still water = 9 kmph.