TS 10th Class Maths Solutions Chapter 14 Statistics Ex 14.3

Students can practice 10th Class Maths Textbook SSC Solutions Telangana Chapter 14 Statistics Ex 14.3 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 14 Statistics Exercise 14.3

Question 1.
The following frequency distribution gives the monthly consumption of electricity of 68 consumers of a locality. Find the median, mean and mode of the data and compare them. (AS₄)

Monthly consumption	65-85	85-105	105-125	125-145	145-165	165-185	185-205
Number of consumers	4	5	13	20	14	8	4

Median :
Solution:

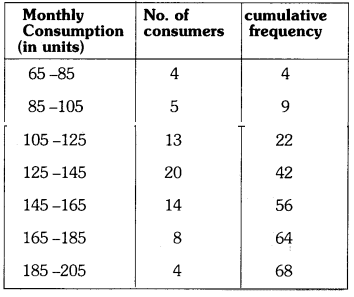
Here n = 68; \(\frac{\mathrm{n}}{2}\) = \(\frac{68}{2}\) = 34
The median lies in the class 125 – 145.
Lower limit (l) of the median class = 125
Frequency of the median class (f) = 20 of (cumulative frequency of the class 105 – 125) = 22
class size (h) = 20
∴ Median = l + \(\frac{\left[\frac{\mathrm{n}}{2}-\mathrm{c.f}\right]}{\mathrm{f}}\) × h
= 125 + \(\frac{\left[\frac{n}{2}-c f\right]}{f}\) × 20
= 125 + 12
= 137 units.

Mean :

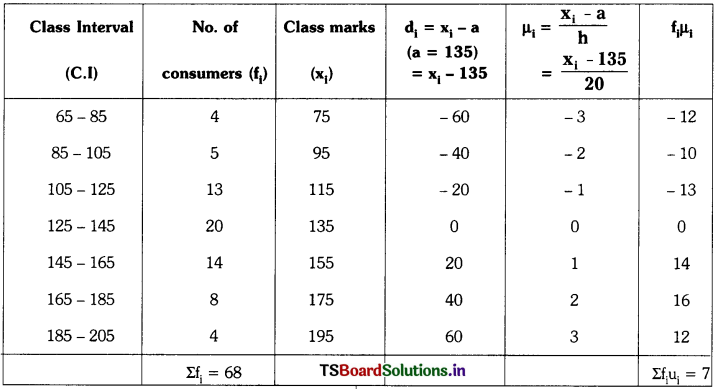
Mean (\(\overline{\mathrm{X}}\)) = a + \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{u}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}\) × h
Here a = 135, h = 20, Σf_i = 68, Σf_iu_i = 7
= 135 + \(\left[\frac{7}{68}\right]\) × 20
= 135 + \(\frac{35}{17}\)
= 135 + 2.05
= 137.05

Mode :
Since the maximum number of consumers have their monthly consumption (in units) in the interval 125 – 145
∴ lower limit of the modal class (l) = 125
class size (h) = 20
Frequency of the modal class (f₁) = 20
Frequency of the class preceding the modal class (f₀) = 13
Frequency of the class succeeding the modal class (f₂) = 14
Modal = l + \(\frac{\left(f_1-f_0\right)}{\left(2 f_1-f_0-f_2\right)}\) × h
= 125 + \(\frac{(20-13)}{(2 \times 20-13-14)}\) × 20
= 125 + \(\frac{7}{(40-13-14)}\) × 20
= 125 + \(\frac{7 \times 20}{13}\) = 125 + \(\frac{140}{13}\)
= 125 + 10.76 = 135.76 units

Comparison :
In this case, the three measures i.e., mean, median and mode are approximately equal.

Question 2.
If the median of 60 observations, give below is 28.5, find the value of x and y. (AS₁)

Class interval	0-10	10-20	20-30	30-40	40-50	50-60
Frequency	5	x	20	15	y	5

Solution:

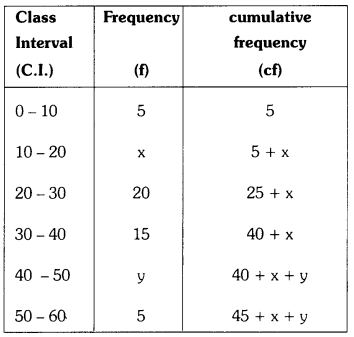
Hence, n = 60 (given)
\(\frac{\mathrm{n}}{2}\) = \(\frac{60}{2}\) = 30
⇒ 45 + x + y = 60
⇒ x + y = 60 – 45 = 15 ……………… (1)
The median is given as 28.5.
If lies in the class 20 – 30.
So, l = 20;
Frequency of the median class (f) = 20
cf (cumulative frequency of the class preceding the median class 10 – 20) = 5 + x
∴ Median = l + \(\frac{\left[\frac{\mathrm{n}}{2}-\mathrm{c.f}\right]}{\mathrm{f}}\) × h
⇒ 28.5 = 20 + \(\left[\frac{30-(5+x)}{20} \times 10\right]\)
⇒ 28.5 = 20 + \(\frac{25-x}{2}\)
⇒ \(\frac{25-x}{2}\) = 28.5 – 20 = 8.5
⇒ 25 – x = 2 × 8.5
⇒ 25 – x = 17
⇒ x = 25 – 17 = 8 ……………… (2)
from (1) and (2) : we get
8 in x + y = 15, 8 + y = 15
∴ y = 15 – 8 = 7
Hence, x = 8 and y = 7

Question 3.
A life insurance agent found the following data about distribution of ages of 100 policy holders. Calculate the median age. (policies are given only to persons having age 18 years onwards but less than 60 years.) (AS₄)

Age (in years)	Below 20	Below 25	Below 30	Below 35	Below 40	Below 45	Below 50	Below 55	Below 60
Number of policy holders	2	6	24	45	78	89	92	98	100

We find the class intervals and their corresponding frequencies to calculate the median age.
Solution:

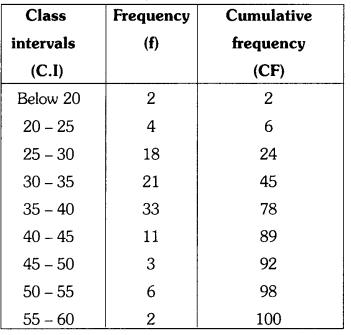
Hence, n = 100: \(\frac{\mathrm{n}}{2}\) = \(\frac{100}{2}\) = 50
The median lies in the class 35 – 40. So l = 35
frequency of the median class (f) = 33
cf (cumulative frequency of the class preceeding the median dass 30 – 35) = 45
class size(h) = 5
∴ Median = l + \(\frac{\left[\frac{\mathrm{n}}{2}-\mathrm{c.f}\right]}{\mathrm{f}}\) × h
= 35 + \(\frac{(50-45)}{33}\) × 5
= 35 + \(\frac{5 \times 5}{33}\) = 35 + \(\frac{25}{33}\)
= 35 + 0.76 = 35.76
Hence, the median age = 35.76 years.

Question 4.
The lengths of 40 leaves of a plant are measured correct to the nearest millimetre and the data obtained Is represented in the following table: (AS₄)

Length (in mm)	118-126	127-135	136-144	145-153	154-162	163-171	172-180
Number of leaves	3	5	9	12	5	4	2

Find the median length of the leaves (Hint : The data needs to be converted to continuous classes for finding the median, since the formula assumes continuous classes. The classes then change to 117.5 – 126.5, 126.5 – 135.5 ………. 171.5 – 180.5)
Solution:

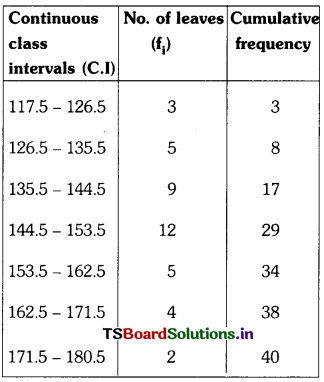
Here, n = 40; \(\frac{\mathrm{n}}{2}\) = \(\frac{40}{2}\) = 20
The median class is 144.5 – 153.5
Lower limit (l) of the median class = 144.5
cf (cumulative frequency of class preceding the median class 144.5 – 153.5) = 17
f (frequency of the median class) = 12
h (class size) = 9
using the formula, median
= l + \(\frac{\left[\frac{\mathrm{n}}{2}-\mathrm{c.f}\right]}{\mathrm{f}}\) × h
= 144.5 + \(\frac{(20-17) \times 9}{12}\) × 9
= 144.5 + \(\frac{3 \times 9}{12}\) = 144.5 + \(\frac{9}{4}\)
= 144.5 + 2.25
= 146.75
∴ Median length = 146.75 mm.

Question 5.
The following table gives the distribution of the life-time of 400 neon lamps

Life time (in hours)	1500-2000	2000-2500	2500-3000	3000-3500	3500-4000	4000-4500	4500-5000
Number of lamps	14	56	60	86	74	62	48

Find the median life time of a lamp. (AS₄)
Solution:

Life time (in hours) class intervals (C.I)	No.of lamps (f)	cumulative frequency (cf)
1500 – 2000	14	14
2000 – 2500	56	70
2500 – 3000	60	130
3000 – 3500	86	216
3500 – 4000	74	290
4000 – 4500	62	352
4500 – 5000	48	400

Here, n = 400; \(\frac{\mathrm{n}}{2}\) = \(\frac{400}{2}\) = 200
The median class is 3000 – 3500
lower limit (1) of the median class = 3000
cf (cumulative frequency of the class preceding the median class 2500 – 3000) = 130
f (frequency of the median class) = 86
h(class size) = 500
using the formula, Median = l + \(\frac{\left[\frac{\mathrm{n}}{2}-\mathrm{c.f}\right]}{\mathrm{f}}\) × h
= 3000 + \(\frac{(200-130) \times 500}{86}\)
= 3000 + \(\frac{70 \times 500}{86}\)
= 3000 + 406.98
= 3406.98 hours
∴ Median life = 3406.98 hours.

Question 6.
loo surnames were randomly picked up from a local telephone directory and the frequency distribution of the number of letters ¡n the English alphabet in the surnames was obtained as follows:

Number of letters	1-4	4-7	7-10	10-13	13-16	16-19
Number of surnames	6	30	40	16	4	4

Determine the median number of letters In the surnames. Find the mean number of letters in the surnames P Also, find the modal size of the surnames. (AS₄)
Solution:
Median:

No.of letters class intervals (C.I)	No.of surnames (f)	cumulative frequency (cf)
1-4	6	6
4-7	30	36
7-10	40	76
10-13	16	92
13-16	4	96
16-19	4	100

Here, n = 100; \(\frac{\mathrm{n}}{2}\) = \(\frac{100}{2}\) = 50
So, the median lies in the class 7 – 10
lower limit (1) of the median class = 7
cf (cumulative frequency of the class preceding median class 7 – 10) = 36
f (frequency of the median class) = 40
h (class size) = 3
using the formula. Median
= l + \(\frac{\left[\frac{\mathrm{n}}{2}-\mathrm{c.f}\right]}{\mathrm{f}}\) × h × h
= 7 + \(\frac{(50-36) \times 3}{40}\)
= 7 + \(\frac{14 \times 3}{40}\) = 7 + \(\frac{21}{20}\)
= 7 + 1.05 = 8.05
Hence, the median of letters in the surnames = 8.05

Mean :

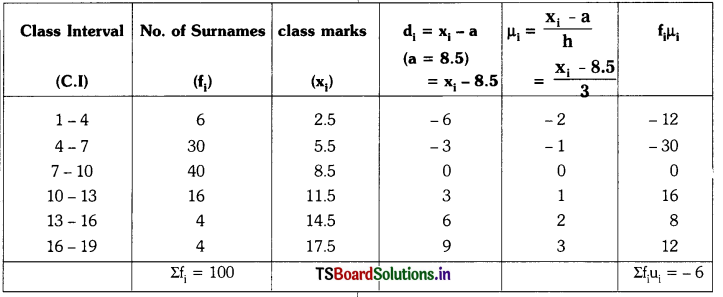
Mean (\(\overline{\mathrm{x}}\)) = a + \(\left[\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{u}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}} \times \mathrm{h}\right]\)
Here a = 8.5, h = 3, Σf_i = 100, Σf_iu_i = -6
= 8.5 – \(\frac{6 \times 3}{100}\)
= 8.5 – \(\frac{18}{100}\)
= 8.5 – 0.18
= 8.32
Hence, the mean of the surnames = 8.32

Mode:

Class intervals (C.I)	Frequency (f)
1-4	6
4-7	30
7-10	40
10-13	16
13-16	4
16 -19	4

Since, the maximum number of surnames have number of letters in the interval 7 – 10, the modal class is 7 – 10
Lower limit (1) of the modal class = 7
frequency of the modal class (f₁) = 40
Frequency of the class preceding the modal class (f₀) = 30
frequency of the class succeeding the modal class (f₂) = 16
class size(h) = 3
∴ Mode = l + \(\left[\frac{\mathrm{f}_1-\mathrm{f}_0}{2 \mathrm{f}_1-\mathrm{f}_0-\mathrm{f}_2}\right]\) × h
= 7 + \(\frac{(40-30)}{(2 \times 40-30-16)}\) × 3
= 7 + \(\left[\frac{10 \times 3}{80-30-16}\right]\)
= 7 + \(\frac{30}{34}\)
= 7 + \(\frac{15}{17}\)
= 7 + 0.88 = 7.88
Hence, the modal size of the surnames = 7.88

Question 7.
The distribution below gives the weights of 30 students of a class. Find the median weight of the students. (AS₄) (Mar ’16 (A.P))

Weight (in kg)	40-45	45-50	50-55	55-60	60-65	65-70	70-75
Number of students	2	3	8	6	6	3	2

Solution:

Class Intervals weight in kgs (C.I)	No.of students (f)	cumulative frequency (cf)
40-45	2	2
45-50	3	5
50 -55	8	13
55-60	6	19
60-65	6	25
65-70	3	28
70-75	2	30

Hence, n = 30; \(\frac{\mathrm{n}}{2}\) = \(\frac{30}{2}\) = 15
So, the median lies in the class 55 – 60
∴ l = 55
frequency of the median class (f) = 6
cf (cumulative frequency, of the class 50 – 55) = 13
class size (h) = 5
∴ Median = l + \(\frac{\left[\frac{\mathrm{n}}{2}-\mathrm{c.f}\right]}{\mathrm{f}}\) × h
= 55 + \(\frac{(15-13) \times 5}{6}\)
= 55 + \(\frac{2 \times 5}{6}\)
= 55 + \(\frac{5}{3}\) = 55 + 1.67
= 56.67
Hence, the median weight of the students = 56.67 kgs.