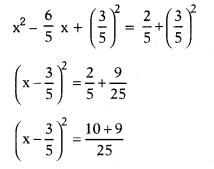TS 10th Class Maths Important Questions Chapter 5 Quadratic Equations

These TS 10th Class Maths Chapter Wise Important Questions Chapter 5 Quadratic Equations given here will help you to solve different types of questions.

TS 10th Class Maths Important Questions Chapter 5 Quadratic Equations

Previous Exams Questions

Question 1.
Write the roots of quadratic equation ax² + bx + c = 0 when b² – 4ac ≥ 0. (A.P.Mar. 15)
Solution:
When b² – 4ac ≥ 0 then the roots of given quadratic equation,
ax² + bx + c = 0 are
\(\frac{-b+\sqrt{b^2-4 a c}}{2 a}\) and \(\frac{-b-\sqrt{b^2-4 a c}}{2 a}\)

Question 2.
Write the two roots of quadratic equation ax² + bx + c = 0 when b² – 4ac = 0 is given.
Solution:
When b² – 4ac = 0 then the roots of given quadratic equation ax² + bx + c =0 are
\(\frac{-b}{2 a}\) and \(\frac{-b}{2 a}\) that means they are equal to \(\frac{-b}{2 a}\).

Question 3.
What do you say about the roots of the quadratic equation ax² + bx + c = 0 when b² – 4ac > 0 is given. (A.P. Mar. ’16)
Solution:
The discriminant b² – 4ac > 0 of the quadratic equation ax² + bx + c = 0 is positive. Hence its roots are real and unequal.

Question 4.
Find the value of k in the quadratic equation 9x² + kx + 1 = 0 when its roots are equal. (T.S.Mar. 16)
Solution:
We know the roots of a quadratic equation are equal if and only if its discriminant is zero, i.e. for ax² + bx + c = 0, b² – 4ac = 0 here a = 9, b = k, c = 1
then b² – 4ac = 0 becomes
k² – 4.9.1 = 0
⇒ k – 36 = 0
∴ k² = 36 and k = \(\sqrt{36}\) = ±6
So k = ±6.

Question 5.
If sum of squares of two consecutive positive even number is 100 then find them. (T.S.Mar. 16)
Solution:
Let the first positive even number = x say
Then its square = x²
The consecutive even number = x + 2
Then square of it = (x + 2)²
Sum of squares of above two
⇒ (x)² + (x + 2)² = 100
⇒ x² + x² + 4x + 4 = 100
⇒ 2x² + 4x + 4 – 100 = 0
⇒ 2x² + 4x – 96 = 0
⇒ x² + 2x – 48 = 0
⇒ x² + 8x – 6x – 48 = 0
⇒ x(x + 8) – 6(x + 8) = 0
⇒ (x – 6) (x + 8) = 0
⇒ x – 6 = 0 or x + 8 = 0
⇒ x = 6 or x = -8
We consider x = 6 only because it is a positive even.
⇒ x + 2 = 6 + 2 = 8
Then the given numbers are 6 and 8

Verification :
6² + 8² =36 + 64 = 100. So verified.

Additional Questions

Question 1.
Check whether the following are quadratic equations or not.
i) (x + 2)² = 3(x – 4)
ii) x² – 3x = -4(2 – x)
iii) (x – 1) (x + 2) = (x + 1) (x + 3)
iv) (x – 3)² = x² + 5x + 6
v) (x + 1)³ = 3x(x² – 2)

i) (x + 2)² = 3(x – 4)
Solution:
Given (x + 2)² = 3(x – 4)
⇒ x² + 4x + 4 = 3x – 12
⇒ x² + 4x – 3x + 4 + 12 = 0
⇒ x² + x + 16 = 0 is a Q.E.

ii) x² – 3x = -4(2 – x)
Solution:
Given x² – 3x = -4(2 – x)
⇒ x² – 3x = -8 + 4x
⇒ x² – 3x – 4x + 8 = 0
⇒ x² – 7x + 6 = 0 is a Q.E.

iii) (x – 1) (x + 2) = (x + 1) (x + 3)
Solution:
Given (x – 1) (x + 2) = (x + 1) (x + 3)
⇒ x² + 2x – x – 2 = x² + 3x + x + 3
⇒ x – 2 = 4x + 3
⇒ 4x – x + 3 + 2 = 0
⇒ 3x + 5 = 0 in not a Q.E.

iv) (x – 3)² = x² + 5x + 6
Solution:
Given (x – 3)² = x² + 5x + 6
⇒ x² – 6x + 9
⇒ x² + 5x + 6 = x² + 5x + 6
-6x – 5x + 9 – 6 = 0
⇒ -11x + 3 = 0
⇒ 11x – 3 = 0 is not a Q.E.

v) (x + 1)³ = 3x(x² – 2)
Solution:
⇒ x³ + 1 + 3x² + 3x = 3x³ – 6x
[∴ (a + b)³ = a³ + b³ + 3a²b + 3ab²]
⇒ x³ – 3x³ + 3x² + 3x + 6x + 1 = 0
⇒ -2x³ + 3x² + 9x + 1 ≥ 0 is not a Q.E.
(∴ degree = 3)

Question 2.
Represent the following situations in the form of quadratic equations.
i) The area of a rectangular plot is 150 m². The length of the plot is two more than thrice its breadth. We have to find the length and breadth of the plot.
ii) The product of the consecutive positive integers is 462. We need to find the integers.
iii) Bhuvan’s mother is 25 years older than him. Their product of their ages after 4 years will be 350 years. We need to find Bhuvan’s present age.

i) The area of a rectangular plot is 150 m2. The length of the plot is two more than thrice its breadth. We have to find the length and breadth of the plot.
Solution:
Let the breadth of the rectangular plot be x m
Then its length (by the problem) = 3x + 2
Now Area of plot = length × breadth
= (3x + 2) × x
= 3x² + 2x
But given area = 150 m²
⇒ 3x² + 2x = 150
⇒ 3x² + 2x – 150 = 0
Where x is the breadth of the plot.

ii) The product of the conseuctive positive integers is 462. We need to find the integers.
Solution:
Let the consecutive integers be x and x + 1.
Their product = x(x + 1) = x² + x
By the problem x² + x = 462
⇒ x² + x – 462 = 0
Where x is the smaller integer,

iii) Bhuvan’s mother is 25 years older than him. Their product of their ages after 4 years will be 350 years. We need to find Bhuvan’s present age.
Solution:
Let the present are of Bhuvan be x years.
Then age of Bhuvan’s mother = x + 25
After 4 years :
Age of Bhuvan would be = x + 4
Bhuvan’s mother’s age would be = (x + 25) + 4
= x + 29
By the problem, (x + 4) (x + 29) = 350
⇒ x(x + 29) + 4(x + 29) = 350
⇒ x² + 29x + 4x + 116 = 350
⇒ x² + 33x + 116 – 350 = 0
⇒ x² + 33x – 234 = 0
Where x is Bhuvan’s present age.

Question 3.
Find the roots of the following quadratic equations by factorisation.

i) x² – 6x + 5 = 0
ii) 2x² – 7x + 6 = 0
iii) x(x + 7) = -12
iv) 3x² + 7x – 6 = 0

i) x² – 6x + 5 = 0
Solution:
Given x² – 6x + 5 = 0
x² – x – 5x + 5 = 0
x(x – 1) -5(x – 1) = 0
⇒ x – 1 = 0 or x – 5 = 0
⇒ x = 1 or x = 5
⇒ x = 1 or 5

ii) 2x² – 7x + 6 = 0
Solution:
Given 2x² – 7x + 6 = 0
⇒ 2x² – 4x – 3x + 6 = 0
⇒ 2x(x – 2) -3(x – 2) = 0
⇒ (x – 2) (2x – 3) = 0
⇒ x – 2 = 0 or 2x – 3 = 0
⇒ x = 2 or 2x = 3 ⇒ x = \(\frac{3}{2}\)
⇒ x = 2 or \(\frac{3}{2}\)

iii) x(x + 7) = -12
Solution:
Given x(x + 7) = -12
⇒ x² + 7x = -12
⇒ x² + 7x + 12 = 0
⇒ x² + 4x + 3x + 12 = 0
⇒ x(x + 4) + 3(x + 4) = 0
⇒ (x + 4) (x + 3) = 0
⇒ x + 4 = 0 or x + 3 = 0
⇒ x = -4 or x = -3
⇒ x = -4 or -3

iv) 3x² + 7x – 6 = 0
Solution:
Given 3x² + 7x – 6 = 0
⇒ 3x² + 9x – 2x – 6 = 0
⇒ 3x(x + 3) – 2(x + 3) = 0
⇒ (x + 3) (3x – 2) = 0
⇒ x + 3 = 0 or 3x – 2 = 0
⇒ x = -3 or n = \(\frac{2}{3}\)

Question 4.
Find two numbers whose sum is 10 and product is 24.
Solution:
Let a number be x.
Then the other number = 10 – x
By Problem, product of numbers = 24
⇒ x(10 – x) = 24
⇒ 10x – x² = 24
⇒ x² – 10x + 24 = 0
⇒ x² – 4x – 6x + 24 = 0
⇒ x(x – 4) – 6(x – 4) = 0
⇒ (x – 4) (x – 6) = 0
⇒ x – 4 = 0 or n – 6 = 0
⇒ x = 4 or n = 6
∴ The numbers are 4, 10 – 4 = 6 or 6, 10 – 6 = 4
6, 10 – 6 = 4

Question 5.
Find the consecutive positive integers, sum of whose squares is 145.
Solution:
Let a positive integer be x.
Then the second integer = x + 1.
By the problem, sum of the squares of the above integers = 145
⇒ x² + (x + 1)² = 145
⇒ x² + x² + 1 + 2x = 145
⇒ 2x² + 2x + 1 – 145 = 0
⇒ 2x² + 2x – 144 = 0 (Dividing by 2)
⇒ x² + x – 72 = 0
⇒ x² + 9x – 8x – 72 = 0
⇒ x(x + 9) – 8(x + 9) = 0
⇒ (x + 9) (x – 8) = 0
⇒ x + 9 = 0 or x – 8 = 0
⇒ x = -9 or x = 8
The numbers are 8, 8 + 1 = 9; 8, 9
(∴ We have to take positive integers)

Question 6.
The base of a right angle is 7 cm more than its altitude. If the hypotenuse is 13 cm, find the other two sides.
Solution:
Let the altitude of the right angle = x cm
Thenitsbase = x + 7 cm

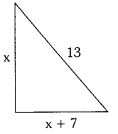
By pythagoras theorem,
(base)² + (height)² = (hypotenuse)²
(x + 7)² + x² = 13²
⇒ x² +49 + 14x + x² = 169
⇒ 2x² + 14x + 169 – 49 = 0
⇒ 2x² + 14x – 120 = 0 (Dividing by 2)
⇒ x² + 7x – 60 = 0
⇒ x² + 12x – 5x – 60 = 0
⇒ x(x + 12) – 5(x + 12) = 0
⇒ (x + 12) (x – 5) = 0
⇒ x + 12 = 0 or x – 5 = 0
⇒ x = -12 or x = 5
Take x = 5 (∴ x cannot be negative)
and x + 7 = 5 + 7 = 12
∴ The two sides are 5 cm and 12 cm.

Question 7.
Find the dimensions of a rectangle whose perimeter is 30 metres and whose area is 50 square meters.
Solution:
Let the length of the rectangle = x
Given perimeter = 2(l + b) = 30
⇒ l + b = \(\frac{30}{2}\) = 15
∴ Breadth of the rectangle = 15 – x
But Area = Length × Breadth
= x(15 – x)
= 15x – x²
By the problem, 15x – x² = 50
⇒ x² – 15x + 50 = 0
⇒ x² – 10x – 5x + 50 = 0
⇒ x(x – 10) – 5(x – 10) = 0
⇒ (x – 10) (x – 5) = 0
⇒ x = 10 or 5
∴ Length 10 m or 5 m
Then breadth = 15 – 10 or 15 – 5
= 5 m = 10 m

Question 8.
Find the roots of the following quadratic equations, If they exist, by the method of the completing the square.
i) x² + 5x = 4
ii) 4x² + 6x = 3

i) x² + 5x = 4
Solution:
Given x² + 5x = 4
⇒ x² + 2.5 x \(\frac{5}{2}\) = 4
⇒ x² + 2. x. \(\frac{5}{2}\) = 4
Now L.H.S is of the form a² + 2ab
When b = \(\frac{5}{2}\)
Adding b² = (\(\frac{5}{2}\))² = \(\frac{25}{4}\) on both sideswe get

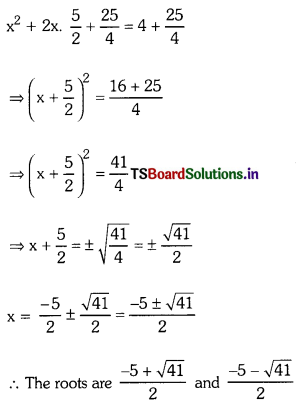
ii) 4x² + 6x³
Solution:
Given 4x² + 6x = 3
⇒ (2x)² + 2.(2x) \(\frac{3}{2}\) = 3
Now LH.S is of the form a² + 2ab
When b = \(\frac{3}{2}\)
Adding b² = (\(\frac{3}{2}\))² = \(\frac{9}{4}\) on both sides

Question 9.
Find the roots of the following quadratic equations by applying the quadratic formula.

i) 3x² + 4x – 12 = 0
ii) 2x² + 2\(\sqrt{3}\)x – 3 = 0

i) 3x² + 4x – 12 = 0
Solution:
Given 3x² + 4x – 12 = 0
Comparing this quadratic equation with ax² + bx + c = 0
a = 3, b = 4, c = -12

ii) 2x² + 2\(\sqrt{3}\)x – 3 = 0
Solution:
Given 2x² + 2\(\sqrt{3}\)x – 3 = 0
Comparing this quadratic equation with ax² + bx + c = 0
a = 2, b = 2\(\sqrt{3}\), c = -3

Question 10.
The sum of the reciprocals of Mohans ages (in years) 2 years ago and 3 years from now is \(\frac{9}{14}\). Find his present age.
Solution:
Let the present age of Mohan be x years
2 years ago Mohan’s age = x – 2
and its receprocal is \(\frac{1}{x-2}\)
Mohans age 3 years from now = x + 3
and its reciprocal is \(\frac{1}{x+3}\)
The sum of the reciprocals = \(\frac{1}{x-2}\) + \(\frac{1}{x+3}\)
= \(\frac{x+3+x-2}{(x-2)(x+3)}\)
= \(\frac{2 x+1}{x^2+3 x-2 x-6}\) = \(\frac{2 x+1}{x^2+x-6}\)
By problem, \(\frac{2 x+1}{x^2+x-6}\) = \(\frac{9}{14}\)
⇒ 9(x² + x – 6) = 14(2x + 1)
⇒ 9x² + 9x – 54 = 28x + 14
⇒ 9x² + 9x – 28x – 54 – 14 = 0
⇒ 9x² – 19x – 68 = 0
⇒ 9x² – 36x + 17x – 68 = 0
⇒ 9x(x – 4) + 17(x – 4) = 0
⇒ (x – 4)(9x + 17) = 0
⇒ x = 4 or x = \(\frac{-17}{9}\)
But x can’t be negative
x = 4
i.e., present age of Mohan = x = 4 years.

Question 11.
In a class test, the sum of Radhika’s marks in Physics and English is 40. If she got 3 marks more in physics and 4 marks less in English, the product of her marks would have been 338. Find her marks in the two subjects.
Solution:
Sum of the marks in Physics and English = 40
Let Radhika’s marks in physics be x
Then her marks in English = 40 – x
If she got 3 more marks in Physics.
Then her marks would be x + 3
If she got 4 marks less in English, then her marks would be 40 – x – 4 = 36 – x
By problem, (x + 3) (36 – x) = 338
⇒ 36x – x² + 108 – 3x = 338
⇒ -x² + 33x + 108 – 338 = 0
⇒ -x² + 33x – 230 = 0
⇒ x² – 33x + 230 = 0
⇒ x² – 10x – 23x + 230 = 0
⇒ x(x – 10) – 23(x – 10) = 0
⇒ (x – 10) (x – 23) = 0
⇒ x – 10 = 0 or x – 23 = 0
⇒ x = 10 or 23
If x = 10, then marks in Physics = 12 and English = 40 – 12 = 28
If x = 23, then marks in Physics = 23 and English = 40 – 23 = 17

Question 12.
The difference of square of larger number and 5 times the larger number is 104. What are the larger number and smaller number ?
Solution:
Let the larger number be ‘x’ and the smaller number be 5x.
By the problem x² – 5x = 104
⇒ x² – 5x – 104 = 0
⇒ x² – 13x + 8x – 104 = 0
⇒ x(x – 13) + 8(x – 13) = 0
⇒ (x – 13) (x + 8) = 0
⇒ x – 13 = 0 orx + 8 = 0
⇒ x = 13 or x = -8
But x can’t be negative
x = 13
∴ The larger number = x = 13 and the smaller number = 5x = 5 × 13 = 65.

Question 13.
Find the nature of the roots of the following Quadratic Equations. If real root exists, find them.
i) 3x² – 2x + 4 = 0
ii) 2x² + 4x – 3 = 0

i) 3x² – 2x + 4 = 0
Solution:
Given 3x² – 2x + 4 = 0
Here a = 3, b = -2, c = 4
Discriminant = b² – 4ac
= (-2)² – 4.3.4
= 4 – 48
= -44 < 0
∴ Roots are imaginary

ii) 2x² + 4x – 3 = 0
Solution:
Given 2x² + 4x – 3 = 0
Here a = 2, b = 4, c = -3
Discriminant = b² – 4ac
= 4² – (4.2. – 3)
= 16 + 24
= 40 > 0
∴ The roots are real and distinct.

Question 14.
Find the value of k for each of the following quadratic equations so that they have equal roots.
i) x² – kx + 25 = 0
ii) kx(x – 3) + 9 = 0
Solution:
Given x² – kx + 25 = 0
Here a = 1, b = -k, c = 25
As this Q.E. has equal roots.
b² – 4ac = 0
(-k)² – 4.1.25 = 0
⇒ k² – 100 = 0
⇒ k² = 100
⇒ k = ± \(\sqrt{100}\) = ± 10
∴ k = ± 10

ii) kx(x – 3) + 9 = 0
Solution:
Given kx(x – 3) + 9 = 0
⇒ kx² – 3kx + 9 = 0
Here a = k, b = -3k, c = 9
As this Q.E. has equal roots
b² – 4ac = 0
(-3k)² – 4.k.9 = 0
⇒ 9k² – 36k = 0
⇒ 9k(k – 4) = 0
⇒ k = 0, or k – 4 = 0
⇒ k = 0 or k = 4
But k = 0 is trival
∴ k = 4

Question 15.
Is it possible to design a rectangular garden whose length is 4 times its breadth, and the area is 3600 m² ? If so, find its length and breadth.
Solution:
Let the breadth = x m
Then length = 4x m
Area = length × breadth
= 4x × x = 4x² m²
By problem, 4x² = 3600
⇒ x² = 900
⇒ x = ± \(\sqrt{900}\) = ± 30
∴ Breadth = x = 30 m and length = 4x = 4 × 30 = 120 m

Question 16.
Write the quadratic equation whose roots are the solutions of 2x + y = 7 and x – y = 2. (AP-SA-I : 2016)
Solution:
Given equations are 2x + y = 7 —- (1)
and x – y = 2 —- (2)
Solving the above equations

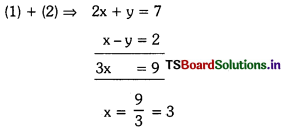
Substituting x = 3 in equation (2)
3 – y = 2
⇒ -y = 2 – 3 = -1
⇒ -y = -1
y = 1
∴ Solutions of (1) and (2) are x = 3, y = 1
Which are the roots of required quadratic equation.
∴ Required quadratic equation is (x – 3) (x – 1) = 0
⇒ x² – x – 3x + 3 = 0
x² – 4x + 3 = 0

Question 17.
Solve the equation 3^x = 5^x + 2. (AP-SA-1:2016)
Solution:
3^x = 5^x+2
Take log on both sides. log3x = log 5X+2
x log 3 = (x + 2) log 5 [log a^m = m log a]
x log 3 = x log 5 + 2 log 5
x[log 3 – log 5] = 2 log 5
x = \(\frac{2 \log 5}{\log 3-\log 5}\)

Question 18.
Find the roots of the equation 5x² – 6x – 2 = 0 by the method of completing square. (AP – SA -1:2016)
Solution:
5x² – 6x – 2 = 0
5x² – 6x = 2
\(\frac{5 x^2}{5}\) – \(\frac{6}{5}\) = \(\frac{2}{5}\)
x² – \(\frac{6}{5}\)x =\(\frac{2}{5}\)
Add (\(\frac{3}{5}\))² on both sides